一种任意重积分自适应递归式快速计算方法
2021-04-13裴永臣关景晗王佳炜
裴永臣, 关景晗, 王佳炜
(吉林大学机械与航空航天工程学院, 长春 130025)

关于数值积分,中外学者还进行了各方面研究[6-8]。张建斌等[9]设计出了基于MATLAB的数值积分求解器,实现了数值积分的可视化功能。陈付龙[10]讨论了二元数值积分的计算方法,并给出了部分C语言代码。唐珺等[11]将递归算法与自适应积分结合用于定积分计算,与辛普森积分相比减少了计算量。还有学者利用遗传算法[12]、神经网络算法[13-15]、粒子群算法[16]、混沌布谷鸟算法[17]计算数值积分。Angulo等[18]将数值积分应用于红细胞生长模型研究。尽管涉及数值积分的研究较多,但是对于三重以上积分数值计算的讨论相对较少。
此外,当前广泛使用的各类科学计算软件具备一定的数值积分计算功能,如著名的MATLAB、Maple、Mathematica等,其数值逼近方法大大加快了复杂积分计算速度。然而,这些科学计算软件自带函数所能计算的积分重数普遍也不高于三重。例如,MATLAB软件虽然具有强大的矩阵运算能力,能够很好地胜任数据计算这一烦琐工作,但能够进行数值积分的自带函数只有quad、dbquad、triplequad三种,分别为一重、二重、三重积分函数,也就是说MATLAB自带函数最多只能计算三重积分,远不能满足科学研究和工程应用需要。
为了提高科学计算软件的积分计算重数,根据多重积分的解析计算方式将累次积分的思想应用于数值积分中[19],现提出一种任意重积分自适应递归式快速计算方法(简称“自适应递归法”)。首先,详细介绍了任意重积分的算法思路,并将递归过程分为递推(划分积分区间)和回归(求解函数值)两部分进行阐述。其次,以MATLAB为例,该方法由积分区间、多重积分函数和被积函数表达式三部分组成。其中,多重积分函数采用递归算法和自适应辛普森公式,具有独立性和自适应性,即当积分重数改变时多重积分函数能够自动适应变化,而无需重新进行编程,避免了重复性操作。最后,结合算例,讨论了该方法与近似三重积分法[3]和辛普森法[19]三者之间的差别。
1 算法思路
递归算法在程序设计中被经常用到。程序编写过程中如果程序运行时又调用了其本身,称这种编写方式为递归[20]。采用递归算法可以将一个复杂问题一层一层转化为多个较原问题更为简单的小问题求解,有效地缩短了程序编写的代码长度。同时递归需要有递归出口,当满足递归出口的约束条件时,递归结束。
该方法可用于求解已知被积函数表达式的任意重积分,得到该积分数值解。具体计算步骤如下。
设任意重积分为

P3,…)dX1dX2…dXn
(1)
式(1)中:a1,a2,…,an为积分下限;b1,b2,…,bn为积分上限;X1,X2,…,Xn为积分变量;P1,P2,P3,…为可变参数。
(1)根据实际生产或研究需求,输入被积函数为
f(X1,X2,…,Xn,P1,P2,P3,…)
(2)
(2)输入问题求解每个积分变量的积分参数(积分下限、积分上限和误差容限),并以积分参数矩阵的形式给出。积分参数矩阵A为n行3列矩阵,即
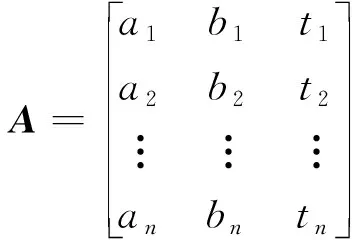
(3)
式(3)中:第i行元素ai、bi、ti为第i个积分变量的积分下限、积分上限、误差容限。
(3)设置递归出口,若积分参数矩阵A行数为0,则递归终止。
(4)读取积分参数矩阵A中第1个积分变量的积分参数。
(5)删除积分参数矩阵A中第1个积分变量的积分参数,即删去第一行。
(6)根据步骤(4)中读取的第1个积分变量的积分下限、积分上限,将积分区间划分成m份,即积分节点为m+1个。由步骤(4)、步骤(5)知,如若重复执行步骤(4)时,相当于第i次执行时读取的是积分参数矩阵A中第i个积分变量的积分参数。第i个积分变量的积分区间划分为
bi-2hibi-hibi]
(4)

第i个积分变量的积分节点对应函数为

(5)
(7)再次执行步骤(4)~步骤(6),直到满足步骤(3)中约束条件,递归终止,此时利用数值积分公式回归求解。
以上步骤的执行流程如图1所示。

图1 积分流程示意图Fig.1 Schematic diagram of integration process
2 递归过程
整个递归过程分为两步:第一步,递推,依次划分各积分变量的积分区间,从积分变量X1到积分变量Xn;第二步,回归,反向求解各积分节点处函数值,从函数fn到函数f1。
2.1 递推:划分积分区间
求解任意重积分与定积分数值计算方法的具体实施过程相似。定积分数值计算方法先确定被划分后的积分节点及其所对应的函数值,然后利用数值积分公式得到数值解。此外,该方法与解析方法虽然在求解形式上有所不同,但两者的求解思路存在相同之处,即递归方法,求解n重积分时,先求解n-1重积分;而求解n-1重积分时,可先求n-2重积分;依次递推直到最后求解的是定积分。于是任意重积分问题可转化为定积分问题来求解。将任意重积分看作求X1的积分,将其他未赋值积分变量暂时看作已知量,用Yn-1表示,此时的被积函数用f1(X1,Yn-1)表示。于是式(1)又可写成下面的形式,即
总是会有不同程度路面路基问题出现在道路桥梁在交付使用后,受到外界环境的影响,会降低道路桥梁使用年限,影响桥梁的质量并加重之前质量问题。所以,要求有关技术人员定期检查破损的路基路面情况,维修排水系统,重视好后期的保养及维护,及时上报并做好相应记录,便于市政工程团队人员的修复。总而言之,需全面提升路基路面施工质量,加强后期维护及保养。
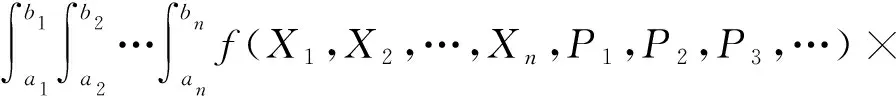

(6)
此时,任意重积分转化成定积分问题,利用定积分数值计算方法即可得到该问题数值解。然而,被划分后的积分节点对应的函数值中含有未赋值积分变量X2,X3,…,Xn,无法确定f1(X1,Yn-1)的值。因此,只有当f1(X1,Yn-1)的值确定后,才能通过数值积分公式得到该问题数值解。由于f1(X1,Yn-1)中含有未赋值积分变量,故再次执行步骤(4)~步骤(6)。f1(X1,Yn-1)中X1已知,所以求解f1(X1,Yn-1)相当于求解n-1重积分,可以看作是X1被赋值后求X2的积分,其他未赋值积分变量X3,X4,…,Xn暂时看作已知量,用Yn-2表示。此时的被积函数表达式用f2(X2,Yn-2)表示。f1(X1,Yn-1)与f2(X2,Yn-2)关系为
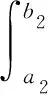
(7)
此时,n-1重积分转化成定积分问题,利用定积分数值计算方法即得到该问题数值解。然而,被划分后的积分节点对应的函数值中含有未赋值积分变量X3,X4,…,Xn,无法确定f2(X2,Yn-2)的值。因此,只有当f2(X2,Yn-2)的值确定后,才能通过数值积分公式得到该问题数值解。由于f2(X2,Yn-2)中含有未赋值的积分变量,故再次执行步骤(4)~步骤(6)。
以此类推,fi(Xi,Yn-i)的求解相当于求解n-i重积分,……,fn-1(Xn-1,Y1)的求解相当于求解定积分,即

(8)
式中:Yn-i为Xi+1,Xi+2,…,Xn的集合。
X1的各积分节点对应函数中X1的赋值均为该积分节点,故可将f1(X1,Yn-1)分成m+1组,然后再根据X2的积分节点将之前每组函数再次分成了m+1组。以此类推,直到Xn的积分节点将Xn-1每组函数再次分成了m+1组。根据积分变量数和各积分变量的积分节点数,最终求解的函数共有(m+1)n个。前后两次调用的函数求解关系如图2所示,即前一次调用的积分变量的每个积分节点对应函数值是通过后一次调用的积分变量的所有积分节点对应函数值通过数值积分公式求解而得。

函数的上角标代表赋值的不同积分节点,下角标与所求解积分变量的下角标相对应图2 各积分变量的积分节点对应函数树状图Fig.2 Tree diagram of the corresponding functions of the integration nodes of each integration variable
2.2 回归:求解函数值
整个递归过程中函数求解关系可以通过图2得知,函数中各积分变量的详细赋值如图3所示,图2中倒数第一行函数值均可通过图3中相应位置以及其祖先节点所在位置的积分节点求得。

图3 积分节点对应函数的积分变量赋值树状图Fig.3 Tree diagram of integral variable assignment of function corresponding to integral node
结合图2、图3,图2中只有函数fn中无未赋值积分变量。也就是说,仅当函数fn的值确定后,才能通过数值积分公式进一步求解函数fn-1的值。函数fn-1的值确定后,可根据积分变量Xn-1的积分节点,求得函数fn-2的值。以此类推,最终求得该任意重积分数值解。
3 MATLAB算法实现
在MATLAB中,本文方法所用的数值积分基层算法是quad函数自带的自适应辛普森公式。程序共有三个脚本,文件名分别为mm.m、multiquad.m、myfun.m,其中mm.m为主程序文件,multiquad.m为多重积分函数multiquad定义文件(在计算中无需改动),myfun.m为多变量被积函数myfun定义文件,运行时只需运行主程序即可。
3.1 主程序说明
该方法主程序如下:
clear;clc
P1=* ; P2=* ; … % P1, P2,…是多变量被积函数myfun必要的可变参数
A=[a1,b1,t1;a2,b2,t2;…;ai,bi,ti;…;an,bn,tn] %积分参数矩阵
Ip=multiquad([],[],A,@myfun,P1,P2,…) %调用多重积分函数multiquad
3.2 多重积分函数multiquad定义
主程序中调用的多重积分函数multiquad,定义为I=multiquad([],[],A,@myfun,P1,P2,…)。前两个参数用于程序运行过程中的数据传递,主程序中初始设定为空矩阵,myfun表示为多变量被积函数。多重积分函数multiquad以MATLAB自带积分函数quad为基层算法求解核心,因此具有自适应性,通过多次调用达到求解任意重积分目的。多重积分函数multiquad定义如下:
function [I]=multiquad(x,X0,A,int_fun,varargin)
a=A(1,1); %积分下限
b=A(1,2); %积分上限
t=A(1,3); %误差容限
A(1,:)=[]; %删除积分参数矩阵A第一行
if size(A,1)==0
I=zeros(size(x));
for i=1:length(x)
I(i)=quad(@f_multiquad,a,b,t,[],[X0;x(i)],int_fun,varargin{:}); %使用函数quad进行计算
end
elseif size(A,1)>0
if length(x)==0
I=quad(@multiquad, a,b,t,[],X0,A,int_fun,varargin{:}); %使用函数quad进行计算
else
I=zeros(size(x));
for i=1:length(x)
I(i)=quad(@multiquad,a,b,t,[],[X0;x(i)],A,int_fun,varargin{:}); %使用函数quad进行计算
end
end
end
函数f_multiquad为多重积分函数multiquad的内部调用函数,用于计算积分区间划分后的各积分节点对应函数值。
function [y]=f_multiquad(x,X0,int_fun,varargin)
if size(X0,1)>0
X=[X0*ones(size(x));x];
else
X=[x];
end
for i=1:size(X,2)
y(i)=feval(int_fun,X(:,i),varargin{:}); %计算指定函数在某点的函数值
end
3.3 多变量被积函数myfun定义
多变量被积函数myfun括号中X为积分变量X1,X2,…,Xn的集合。多变量被积函数myfun接受X,P1,P2,…并返回被积函数值y。主函数中的多变量被积函数myfun定义如下:
function [y]=myfun(X,P1,P2,…)
X1=X(1,:); %积分变量X1
X2=X(2,:); %积分变量X2
⋮
Xn=X(n,:); %积分变量Xn
y=f(X1,X2,…,Xn,P1,P2,P3,…); %被积函数f(X1,X2,…,Xn,P1,P2,P3,…)
4 算例分析
选取三种具有代表性的函数进行程序验证,并将自适应递归法与解析法,近似三重积分法[3]和辛普森法[19]在计算时间和精度上进行了对比。
例1

例2
16+8π≈41.132 741 2。
例3 工程应用
磁力驱动器凭借极高的密封性和无接触特性,被广泛应用于制药、化工、石油、食品等行业[3]。磁力驱动器的内外磁套之间的轴向磁力[3]被写为

(9)

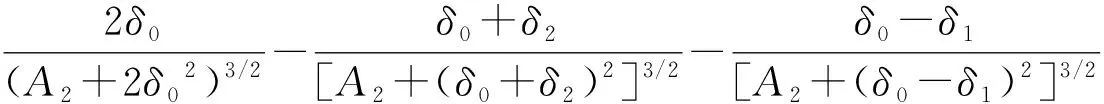
(10)
式(10)中:δ0为内磁套和外磁套之间的相对位移,δ0=0.02 m;δ1为内磁套厚度;δ2为外磁套厚度;A2表示为
A2=(r2sinβ-r1sinα)2+(r2cosβ-r1cosα)2
(11)
磁性套筒的材料参数和尺寸参考文献[3],如表1所示。

表1 磁性套筒的材料参数和尺寸Table 1 Material parameters and dimensions of magnetic sleeve
以上三个算例的计算结果如表2所示。
通过表2得知,例1和例2中,辛普森法(h=0.05)与自适应递归法(ti=10-6)精度相同,辛普森法(h=0.01)与自适应递归法(ti=10-7)精度相同,但计算时间差距明显。例1中,自适应递归法的计算时间与辛普森法相比,分别缩短了69.6%和99.8%。例2中,自适应递归法的计算时间与辛普森法相比,分别缩短了87.8%和99.9%。例3中,近似三重积分法计算磁力驱动器的轴向磁力耗时严重,而辛普森法和自适应递归法能够将计算时间减低到20 s以内。值得注意的是,例3中辛普森法的h只在0.01时有数值解。综合以上算例,本文提出的自适应递归法的计算效率高于近似三重积分法和辛普森法,主要是由于以下两点:

表2 例1、例2和例3的计算结果Table 2 Calculation results of case 1, 2 and 3
(1)辛普森法中的步长h受积分区间的影响。h取值要小于各变量积分区间中的最小值,如例3中h<0.5时则无法求解。这种情况导致了积分区间划分的不合理,尤其是积分上下限差值较大时,过小的h增加了程序的运行时间。此外,辛普森法的积分区间划分方式固定,步长h恒定,增加了不必要的计算量,而自适应递归法巧妙地将各变量积分区间进行了独立划分,并单独设定误差限,实现了计算量的合理分配。自适应递归法可以在保证精度要求的同时有效地降低计算量,避免了辛普森法中因提升精度而导致计算时间呈指数形增长现象的发生。
(2)自适应递归法的优势在于输入各变量积分上下限和被积函数表达式后,即可求解,适应性强,而近似三重积分和辛普森法缺少对积分重数的适应能力。近似三重积分仅能计算四重积分。采用辛普森法计算多重积分,积分重数与程序中的函数TNR_ITG[16]为一一对应关系,而不是自适应递归法中的多对一关系,导致函数TNR_ITG的内容需根据积分重数的变化而不断调整。积分重数与函数TNR_ITG的改动幅度为正相关。
5 结论
针对当前科学计算软件求解积分重数的有限性及传统解析积分的局限性,提出了一种任意重积分自适应递归式快速计算方法。该方法参考定积分计算方式,依次将各积分变量的积分区间进行自适应划分,当完全确定划分后各积分变量的积分节点时,再反向逐层求积,从而实现递归过程。
(1)基于该方法给出了MATLAB中的算法源程序代码,并进行了算例分析,验证了该方法在多重积分求解时的高效率。
(2)与现有方法的比较结果表明,提出的自适应递归法不仅计算时间短、结果精度高,效率高,而且凭借对积分重数的适应能力,省去了不断编写程序的烦琐过程,操作更为方便,具备通用性和普适性。
(3)该方法是直线往复运动磁力驱动器磁力求解问题的一种更简洁、快速且准确的计算方法,可应用于涉及积分运算的实际应用,具有一定的工程应用价值。
