基于欧拉图解的三段论推理教学设计探究

徐培亮 欧阳群英 张洁

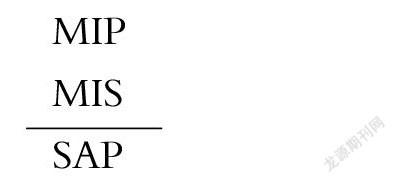
【摘要】欧拉图解在逻辑学教学中運用十分广泛，其目的是使抽象晦涩的逻辑推理变得更具体、更清晰、更形象，以易于学生理解和掌握。欧拉图解遵循一定的判定依据、步骤和注意事项，在三段推理教学中，它可以加深学生对三段论公理的全面理解和对三段论规则的灵活运用。但该方法也存在着画图时间冗长、画图过程繁琐、缺乏简明性等缺点，需通过建立“案例主导”教学模式，精心设计课前预习，综合运用多媒体资源等方式手段弥补不足。

【关键词】欧拉图  三段论  逻辑学

【Abstract】Euler diagram is widely used in logic teaching. Its purpose is to make the abstract and obscure logical reasoning more specific， clearer and more vivid， so as to be easy for students to understand and master. Euler diagram follows certain judgment basis， steps and precautions. In the teaching of syllogism reasoning， it can deepen students comprehensive understanding of syllogism axioms and flexible application of syllogism rules. However， this method also has some disadvantages， such as long drawing time， cumbersome drawing process and lack of simplicity. It needs to make up for the deficiency by establishing a“case led” teaching mode， carefully designing preclass preview， and comprehen⁃sively using multimedia resources.

【Keywords】Euler diagram; Syllogism; Logic

【基金项目】陆军工程大学基础部教育教学课题“军校学员逻辑思维训练体系研究”（JCBJYJX20YB002）。

【中图分类号】G64   【文献标识码】A 【文章编号】2095-3089（2021）19-0153-03

用圆圈表示概念外延的大小及相互关系的方法最早是由18世纪瑞士数学家欧拉（Leonhard Euler，1707-1783）提出的。这种方法借助图形直观地显现了概念间的逻辑关系，被后人称为“欧拉图解”。

欧拉图解在逻辑学的演绎推理教学中多次运用，除概念间的关系外，还可判定性质命题的推理和三段论的推理是否有效。本文的研究对象即欧拉图解在三段论推理教学中的应用。

一、欧拉图解的判定依据、步骤和注意事项

欧拉图解作为逻辑推理的一种方法，同样遵循前提推出结论的过程需符合逻辑的规律和规则这一原则。

（一）欧拉图解的判定依据

一个推理，如果其前提为真，用欧拉图解判定其结论也必然为真，则这个推理的形式是有效的;一个推理，如果前提为真，用欧拉图解判定其结论必然为假，则这个推理的形式是无效的;一个推理，如果前提为真，用欧拉图解判定其结论并非必然为真，则这个推理的形式也是无效的。

（二）欧拉图解的步骤

根据判定依据，用欧拉图解判定一个推理形式是否有效，首先假定推理的前提为真，然后用欧拉图画出前提中涉及到的所有概念之间的关系;其次，用欧拉图再画出结论中涉及到的所有概念之间的关系;再次，用前提中概念之间的关系验证结论中概念之间的关系是否必然为真，如果必然为真，则可判定推理形式有效，如果必然为假或并非必然为真，则可判定推理形式无效;最后，作出判定的结论。

（三）欧拉图解的注意事项

依据上述步骤，用欧拉图解判定推理形式是否有效应注意以下三点：

1.准确画图

准确画图包括“质”和“量”两方面的要求。一是能够用图形无误地表示前提和结论所描述的命题逻辑，此为“质”;二是能将前提和结论所描述的所有命题逻辑无遗漏地表示出来，此为“量”。

2.认真识图

在保质保量准确画图的基础上，假定所有的表示前提命题逻辑的欧拉图为真的情况下，认真识别所有的表示结论命题逻辑的欧拉图的真假，特别是反映同一关系、包含关系、交叉关系的欧拉图，判定它们是否清晰、精准、全面地囊括了前提推导出的种种。

3.谨慎判定

如果表示结论命题逻辑的欧拉图在前提为真的所有欧拉图下皆为真，那么就可以判定结论必然为真，此推理形式有效;如果表示结论命题逻辑的欧拉图在前提为真的所有欧拉图下皆为假，那么就可以判定结论必然为假，此推理形式无效;如果表示结论命题逻辑的欧拉图在前提为真的所有欧拉图下有的为真，有的为假，那么就可以判定结论并非必然为真，此推理形式无效。

二、欧拉图解在三段论推理教学中的运用

三段论是由两个包含着一个共同项的性质判断出发，推出一个新性质判断的推理。因为它包含三个性质判断（直言判断），又称直言三段论。任何一个三段论都包含着三个项：大项（P）、小项（S）和中项（M）。其中，中项（M）即是在前提中都出现，而在结论中不出现的项。①

三段论推理的依据是三段论公理和三段论规则（包括一般规则和特殊规则），只有符合三段论公理和三段论规则的三段论推理才是有效的。

然而在具体教学中，教员费了大力气备课，但仍感到讲得无趣，学员也努力集中精力听讲，可依旧觉得晦涩难以理解。而用欧拉图解判定三段论推理则可让沉闷的课堂“活”起来，加深学生对公理的全面理解和对规则的灵活运用。

例如，现行的逻辑学教材在阐述三段论公理时都用到了三段论的结构式来表达：

所有M是P，                所有M不是P，

所有S是M，                所有S是M，

所以，所有S是P。        所以，所有S不是P。

（结构式一）                 （结构式二）

虽然这两个结构式准确反映了“对一类事物的全部有所断定，那么对该类中任一事物也必定有所断定”的公理内容，但结构式仍是以文字为基础对公理内容进行翻译的，其本质上还需学习者在头脑中自行联想转化，以便吸收接受。

而如果用欧拉图解将公理内容直接展现出来，则更易于让学习者加深理解，如图1、图2。

图1、图2是大部分教材在阐释三段论公理时所采用的欧拉图，但笔者认为，这两幅图并没有全面地解释公理内容。因为公理中涉及的三项概念之间不仅存在着包含关系，还存在着同一关系。而图1反映的P、M、S之间的关系和图2中反映的M、S之间的关系皆为包含关系。

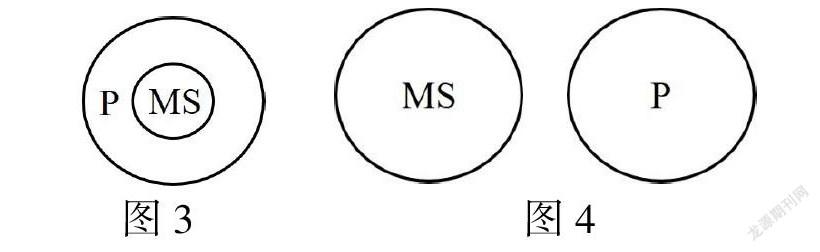
而如果M和S是同一关系的话，那欧拉图解三段论公理内容应如图3、图4所示。

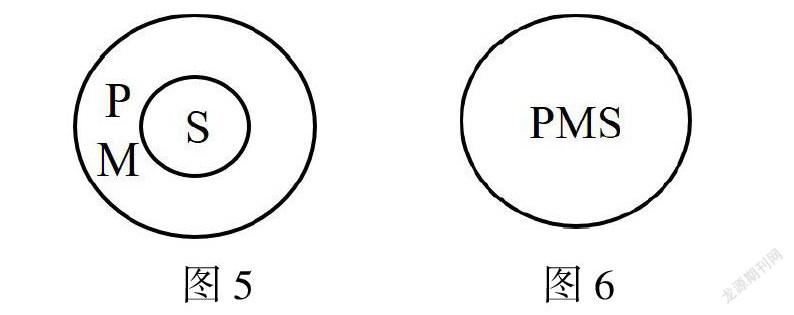
同样，对于结构式一而言，如果P和M是同一关系而M和S是包含关系的话，那欧拉图应如图5所示;如果P、M、S之间互为同一关系的话，那欧拉图应如图6所示。

图1—图6是三段论公理完整的欧拉图解，这六张图不仅全面地阐释了公理内容，也巧妙地将概念与推理间的知识点联结起来，既加深了学生对公理的深入理解，也凸出了课程严密的逻辑特点。

再如，这样一个三段论结构式：

MIP

MIS

SAP

这是一个三段论第三格的结构式，如果根据三段论的规则来判定，这个推理形式很明显是无效的。但在没有掌握三段论的规则前，学生很难通过三段论公理来判定这一推理是否有效。

而如果要讲解三段论第三格的规则②，教师一般会采用反证法来证明，即假设小前提是否定的，根据“前提中有一否定，结论必否定”的一般规则可知结论是否定的，则P是周延的，再根据“在前提中不周延的项，在结论中不得周延”的一般规則可推P在前提中周延，则大前提为否定命题。这样一来，大小前提都为否定命题，又违反了“两否定前提不能得结论”的一般规则。所以，假设不成立，可证明小前提必须肯定。那么，S在前提中就不周延，同理，S在结论中也不得周延，所以，结论只能是特称命题。至此，才算将第三格的规则讲解完整。

但整个推导过程建立在三段论的一般规则基础之上，用到了七个一般规则中的三个。学生只有扎实掌握三段论的一般规则才能够使头脑高速旋转，调动全部思维在头脑中建立抽象的推导流程框架，然后才能顺利理解特殊规则的推导。整个学习虽“烧脑”，但也增加了理解的难度，不利于调动学生的学习积极性和主动性。

而如果用欧拉图解来验证这个三段论是否有效则会使学习变得更直观、更清晰、更具体，使课堂氛围会活跃起来，学习效果也会自然提高。

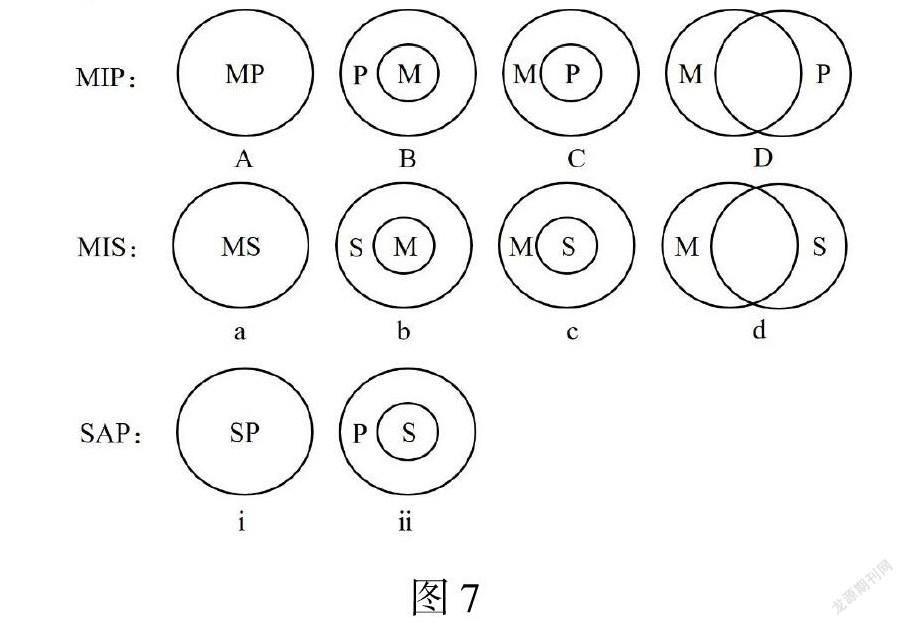
教师引导学生准确画出该三段论大小前提和结论所涉及的所有欧拉图，然后由学生识别验证前提与结论的欧拉图的真假关系，如图7所示。

从图7可以看出，大前提MIP为真的欧拉图有A、B、C、D四个，小前提MIS为真的欧拉图有a、b、c、d四个，结论SAP为真的欧拉图有ⅰ、ⅱ两个。把MIP和MIS的欧拉图结合起来共有16个组合，而能得到结论ⅰ或ⅱ的组合只有2个（A和a、B和c），其他14个组合或者必然得不出结论，或者不必然得出结论。所以，根据欧拉图解的判定依据，该三段论的推理是无效的。

三、欧拉图解的优劣及教学运用策略

从前文所述可以看出，运用欧拉图解，可以从图形中直观清晰地判定出三段论推理是否有效，提升了教学的趣味性。同时，将欧拉图解与探究式学习结合起来，增加了课堂互动，促进学生深度参与课堂，激发了学生学习的主动性和创造性，提升了学习热情和兴趣。而学生运用欧拉图解必然要严格遵循其判定依据、步骤和注意事项，这期间逐步养成严谨的思辨思维和务实的求知精神，又实现了课程思政的目的。

然而，运用欧拉图解，我们也看到了它的劣势：如画图过程耗时，遇到繁琐情况，只能等到所有图形全部画完才能进行识图和判定，而使用图形过多又使得该方法缺乏简明性，造成课时冗长，影响授课进度。

那么该如何扬长避短，发挥欧拉图解在教学中的最大效益呢？

首先，建立“案例主导”的教学模式。将欧拉图解与案例主导相结合，选择贴近学生生活和专业的鲜活案例作为教学资源，运用客观生动的案例使欧拉图反映的概念变抽象为具体;同时通过案例创设情境，学生不再囿于纯理论的分析，而是以特定的身份真实感受逻辑推理，促进学生的独立思考能力和批判性思维能力得到进一步提升。例如，前文所列举的三段论第三格结构式，可以结合当下疫情防控的热点时事展开教学，将某地疫情后网络上的传言作为剖析的具体案例：

某机场部分工作人员是新冠病毒肺炎感染者，

某机场部分工作人员是Z城人，

所以，Z城人都是新冠病毒肺炎感染者。

将结构式情境化，增强了课堂对学生的吸引力，以具体概念画图，学生的感官目标更明确，参与热情也自然会提高。

其次，充分优化课前预习的教学设计。学员在课前完成两项预习任务，一是仔细阅读教材三段论相关知识点的内容，对阅读中产中的推理疑问尝试运用欧拉图解判定，带着未能解决的问题进入课堂寻找答案;二是完成教师安排的线上知识点测试题，自测欧拉图解预习情况。教师在课前通过线上测试结果研判学生对欧拉图解的掌握情况，有针对性地调整授课内容和计划，提高课堂的有效利用率，以弥补画图耗时的不足。

最后，综合运用多媒体教学技术和软件。笔者前期在本校，面向学习“逻辑学基础”课程的部分学生开展了一项问卷调查。结果显示，88.13%的受访者认为，采用音频、视频等多媒体教学资源可以提高知识习得的效果。而运用PS、CAD、Premiere等制图、音视频软件制作教学资源可以最大限度发挥欧拉图解的优势，使图形更鲜活更清晰，满足学生学习需求，符合认知规律，更利于准确识图和精准判定。

注释：

①南开大学哲学院逻辑学教研室.逻辑学基础教程（第三版）[M].天津：南开大学出版社，2014：89.

②三段论第三格规则：小前提必肯定，结论必特称。

参考文献：

[1]汪柏树.性质命题推理有效性的欧拉图解法判定[J].黄山学院学报，2010，12（1）：54-62.

[2]武庆荣.案例教学法在法律逻辑学课程教学中的有效应用[J].贵州工程应用技术学院学报，2017，35（5）：54-57.

[3]文颖丰.多媒体技术在“法律逻辑学”中的应用研究[J].新课程研究，2020（18）：19-20.

作者简介：

徐培亮（1982年-），男，汉族，黑龙江哈尔滨人，陆军工程大学基础部人文教研室讲师，文学硕士，研究方向：逻辑学教学、军事写作教学。