基于不完全互惠偏好关系的产品工业设计方案决策

杨延璞，余 进，王刚锋

(长安大学工程机械学院，陕西 西安 710064)

0 引言

产品工业设计过程的输入是用户需求，输出是满意解，中间环节是“问题”、“解”与“决策”不断交织演化反复迭代的过程[1]。决策是设计过程收敛的必要环节，是联系问题空间与解空间的重要纽带，能够促进产品设计问题到合理解的有效转换。由于产品工业设计过程的多学科性与问题求解过程的模糊性与多解性，科学、合理的决策就显得尤为重要，它不仅关系到产品开发进程能否顺利进行，甚至决定了产品创新设计的成败，设计决策和估计的失误可能给整个设计带来灾难性后果[2]。

产品开发过程中的工业设计决策常需多学科、多行业专家参与，一般涵盖产品方案集、方案属性集与决策专家集，是决策者对产品方案按照属性指标进行信息交互与意见集结的过程，目的是对产品设计方案进行综合评价并确定最优方案。由于产品开发过程涉及多学科知识，基于多属性集的数学决策成为综合评判方案优劣的常用方法，主要包括属性集权重及专家权重确定、决策信息集成、方案排序三个步骤。权重确定方法有主观赋权法、客观赋权法、组合赋权法等。主观赋权法主要由专家根据经验主观判断得到权重，包括德尔菲法(Delphi)[3]、层次分析法(Analytic Hierarchy Process，AHP)[4]等;客观赋权法主要根据各属性在属性集中的变异程度和对其他属性的影响程度，计算数据来源于决策矩阵，包括熵值法[5，6]、主成分分析法[7]、粗糙集[8]、多目标优化法[9]等;组合赋权法是主、客观赋权法的结合[10]。决策信息集成是将个体决策意见集结为群体信息，从而实现对设计方案的排序优选，如逼近理想解排序法(Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS)[11]、表达现实的淘汰与选择法(ELimination Et Choix Traduisant la REalité-elimination and choice expressing reality，ELECTRE)[12]、多准则妥协解排序法(VlseKriterijumska Optimizacija IKompromisno Resenje，VIKOR)法[13]等。设计方案排序是对决策者意见进行处理的过程，常用基于模糊数[14]、区间数[15]、直觉模糊数[16]、语言信息[17]等意见表达与处理方法。产品工业设计过程的多解性、模糊性、感性与理性并存等特点使得设计方案的决策过程具有不确定性，具体表现之一是当决策人员面对多种设计方案进行优劣评判时可能出现犹豫，导致其难以做出决策而造成偏好信息的缺失。而现有产品工业设计决策研究[14，18-20]主要以提高评价结果的科学性和客观性为目标，缺乏对设计决策过程中信息缺失的深入研究。

为此，本文引入不完全互惠偏好关系处理产品工业设计方案决策中的偏好缺失问题。通过对不完全互惠偏好关系的分析，研究了其基本运算法则与偏好缺失值处理算法，提出了产品工业设计方案决策流程。将决策者权重分为一致性权重和信任权重，一致性权重根据决策者对产品方案的不完全互惠偏好矩阵确定，信任权重由决策者互相评判获得，进而得到决策者综合权重;为确定决策群体意见的一致性程度，通过建立共识度模型评判整体偏好一致性，结合决策群体的不完全互惠偏好关系一致性权重和信任权重确定非共识决策的反馈机制，利用粒子群优化算法和最小成本法对不完全互惠偏好矩阵进行优化，促使共识达成，进而输出产品方案整体支配度，确定方案优劣。以汽车充电桩的产品设计方案决策为例，开发了软件原型系统，验证了方法有助于解决工业设计决策中的偏好缺失问题，提升设计决策的质量和效率。

1 不完全互惠偏好关系

产品工业设计的多方案决策建立在针对方案之间优劣判断的基础上，因此引入互惠偏好关系(Reciprocal Preference Relation，RPR)[21]进行处理。设X={x1，x2，…，xn}为产品工业设计方案集，E={e1，e2，…，em}为决策人员集，某一设计决策人员对方案集的评价矩阵为P=(pij)n×n，对∀i，j∈{1，2，…，n}满足pij+pji=1，称P=(pij)n×n为一个互惠偏好关系。当i=j时，pij=pji=0.5，表示两个方案无差异;pij＞0.5表示方案i优于方案j;pij＜2.5则方案j优于方案i。当决策人员对设计方案认知不确定而未能给出两个方案间的偏好关系时，即引起偏好关系的缺失，这样的RPR被称为不完全的RPR[22]。

(1)乘法传递性

对∀i，j，k∈{1，2，…，n}满足pij·pjk·pki=pik·pkj·pji(等式元素非0)，则称该RPR对于方案集X具有乘法传递性[23]。

(2)乘法一致性

对任意两个方案组成(xi，xj)(i＜j)，为估计偏好缺失值，可构建中间方案xk(i＜k＜j)，利用所有可能的乘法传递性估计值的均值使不完全的RPR矩阵P=(pij)n×n成为完全的RPR矩阵MP=(mpij)n×n，描述为:

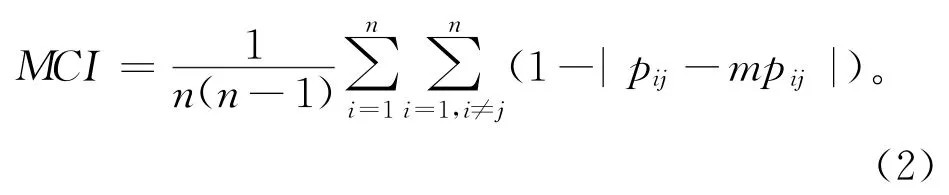
MCI值越大，则设计方案偏好矩阵的一致性就越好。

(3)缺失偏好值计算

对存在偏好关系缺失或未知的不完全的RPR，在决策信息集结时需对缺失值进行补充。基于产品工业设计方案集X，引入中间方案xk，设A={(i，j)|i，j∈{1，2，…，n}∩i≠j}，MV={(i，j)|pijunknown，(i，j)∈A}为偏好关系缺失的方案对的集合，EV=AMV为具有已知偏好关系的方案对的集合。则P中的缺失偏好值计算如下:

2 产品工业设计方案决策流程

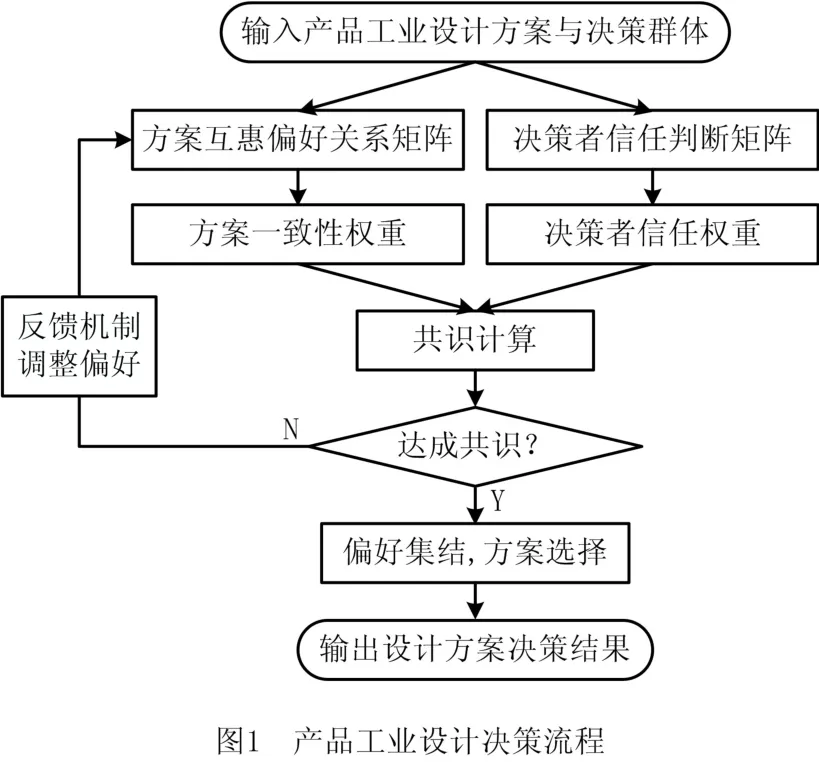
基于互惠偏好关系的产品工业设计决策流程如图1所示，具体包括决策者权重计算、共识过程与方案选择3个阶段。

2.1 决策者权重计算

决策人员权重由一致性权重与信任权重两部分构成。某决策人员的评价矩阵一致性程度越高，则其权重应越大[21]。信任权重反映决策群体中某一决策者被他人信赖的程度，即权威程度。

(1)一致性权重

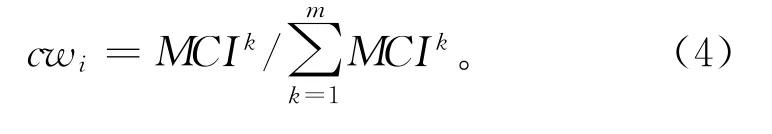
式中:m是决策人员数量，MCIk为第k个决策人员的MCI。

(2)信任权重

信任权重twi采用层次分析法[24]计算，由两两专家互相判断相对权威程度，形成判断矩阵计算信任权重。

(3)综合权重

2.2 共识过程

共识反映了决策群体意见的一致性程度，具有较高共识度的决策结果才有较高的可信度[25]。因此，需建立共识模型并依靠反馈机制对非共识决策进行调整。

2.2.1 共识度计算

则决策群体对方案i和j的意见相似性为:

则决策群体对方案集的共识度为:

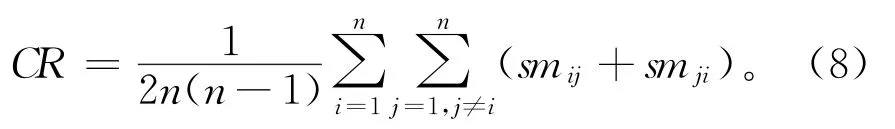
2.2.2 反馈机制

由于工业设计过程的多学科特性，决策人员间存在知识背景、社会经验等方面的差异，使得他们在面对产品设计方案时存在不同认知，共识难以达成绝对一致(CR=1)。为此，需由决策协调者或者决策群体事先设定共识阈值γ，当CR≥γ时，说明决策人员偏好达成一致，否则需引入反馈机制进行共识调整。

(1)确定待修改决策人员

将决策人员的cwi和twi分别与群体一致性权重和信任权重均值进行比较，根据相对均值的高低将其分为4种情况:

1)cwi高，twi高。说明决策者权威性和偏好一致性程度均高，应保持其偏好不变。

2)cwi高，twi低。说明决策者评价矩阵一致性高但权威性低，与其他决策人员存在差异，需对进行偏好调整。

3)cwi低，twi高。说明决策者具有较好的权威性，但评价矩阵一致性程度较低，说明该决策者自身偏好出现矛盾，需进行偏好调整。

4)cwi低，twi低。说明决策者权威性和意见一致性程度均较低，需对偏好进行调整。

据此确定待修改的偏好标识为Rk={(i，j)|cdij＜CR∪∉缺失值}，i，j=1，2，…，n。

(2)偏好调整机制

设偏好调整反馈参数为δ，调整后的偏好值为p'ij，则

式中Pj'为决策人员j调整后的偏好矩阵。

(3)偏好调整

根据共识确定待修改偏好标识为:

偏好调整采用粒子群算法[26]寻找最优解，当偏好矩阵满足共识度要求时，根据最小成本法确定最终偏好矩阵。以共识度为优化目标函数，则粒子群算法的位置与速度更新方式为:

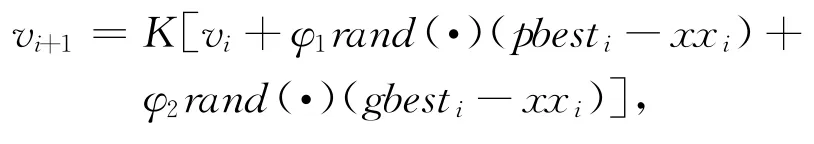
式中:xxi为某一粒子的位置;vi为该粒子的速度;pbesti为该粒子搜索到的最优位置;gbesti为粒子群搜索到的最优位置;rand(·)是随机数函数，生成(0，1)之间的随机数;K为收敛因子，且满足K=，φ=φ1+φ2，φ＞4，通常φ=4.1。

2.3 方案选择

当共识达成后，对产品工业设计方案i的整体偏好计算如下:

则方案xi的整体支配度为:

方案的支配度越大，决策群体的偏好性越强，则应选择支配度最大的方案为合适的解决方案。

3 实例验证

以某型汽车充电桩的设计方案决策为例，企业需求输入为产品造型美观、加工容易实现、充电操作与维护方便、价格成本低廉。其中:造型要求符合对称、比例、均衡等美学法则，体现科技感;加工要求主体采用钣金折弯，避免注塑成型;人机操作主要考量充电枪取放方便性、刷卡充电的易用性、充电急停按钮的使用与防误操作、维修开门的方便性;成本要求从材料选择、板材厚度、喷塑工艺、装配方式等方面进行考虑。经3名工业设计师的前期调研、分析与设计，得到4款设计方案，如图2所示。

组织资深用户(e1，e2)、产品工程师(e3，e4)、市场营销(e5，e6)与管理人员(e7，e8)各两名对4个方案从产品造型、加工难易程度、人机操作、价格成本等方面进行综合评判。若决策人员对某一方案对应指标的两个偏好数据均超出[0，1]的区间，则认为该决策者的偏好失效，将其认定为未知偏好关系(以x或1-x表示);若决策人员对某一方案对应指标的偏好数据其中之一超出[0，1]的区间，则按照另一数据计算该超出数据(若未超出的偏好为x，则计算超出数据的偏好为1-x)。得到4个方案的偏好关系(未知偏好关系以x表示)如下:

(1)不完全偏好处理与权重计算

对未知偏好关系根据式(1)～式(3)进行处理，计算缺失偏好值则可得到完整的RPR。据式(1)～式(5)计算得到各决策者的偏好一致性分别为:0.917，0.837，0.955，0.988，0.920，0.914，0.728，0.826，得到群体一致性权重为:

同时，由决策群体进行两两信任判断，得到信任矩阵为:

利用层次分析法计算，得到一致性指标为0.043，一致性比率为0.03＜0.1，信任矩阵具有良好的一致性，从而得到决策群体的信任权重为:

(2)共识过程

任务下达方为保证决策结果的有效性与决策质量，认为决策人员偏好一致性不低于90%时满足要求，因此设定共识阈值为0.9。将以上算法在MATLAB软件中开发计算程序，得各方案的共识度分别为0.835 6、0.859 4、0.899 3、0.838 8，总体共识度为0.858 3，共识未能达到预设要求，需进行共识调整。方案共识计算程序界面如图3所示。根据群体一致性权重计算结果，偏好矩阵P2、P7、P8一致性程度较低;根据信任权重计算结果，决策者e1、e2、e5、e6的信任权重值低于平均信任权重0.125，据此确定需进行偏好优化的位置。

(3)偏好调整

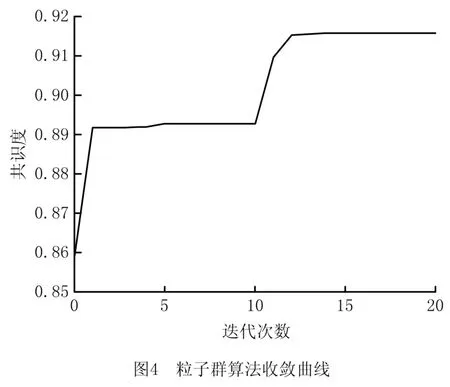
进入粒子群算法优化界面，设定粒子群数量为30，φ1=2，φ2=2.1，收敛因子K=0.729。优化时将第一次完整的RPR作为基础，经多次实验计算发现在7代左右即收敛，因此设定优化代数为10。但初次执行粒子群优化后的共识度最大值为0.893 6，仍不满足共识要求，因此选用第一次优化后的共识度最大且修改成本最小的偏好矩阵作为新的优化基础，此时偏好矩阵如下:

得到各决策者的偏好一致性分别为:0.917，0.963，0.955，0.988，0.920，0.914，0.808，0.899。可以看出，原偏好矩阵P2、P7、P8的一致性得到提升，原其他矩阵一致性保持不变。重新计算群体一致性权重为:

(4)方案支配度计算

从优化后满足共识度要求的偏好矩阵中选取修改成本最小的矩阵作为最终偏好矩阵，则得到4个方案的偏好关系如下:

最终偏好矩阵的总体共识度为0.909 5。利用式(13)和式(14)对这4个方案的偏好关系进行计算，得到其支配度分别为1.892 12、1.404 24、1.596 66、1.106 98，因此方案1为优选方案。粒子群算法寻优与产品方案支配度计算程序界面如图6所示。

4 讨论

(1)由于工业设计过程的多学科与模糊特性，产品设计方案决策中会存在决策信息的缺失或不完备，这给决策信息集结带来了困难。利用不完全的RPR关系对该问题进行描述是一种有效途径，借助乘法传递性对缺失值进行估计是对RPR关系一致性建模的合适方法[22]。但乘法传递性需要依托已知偏好数据估算未知偏好，当某一决策矩阵的偏好完全未知时，该方法即失效，需剔除完全未知偏好数据剔除。

(2)偏好矩阵一致性反映的是决策者对方案的偏好在打分上的统一程度，利用其衡量决策者的偏好一致性程度并和决策者信任权重结合，目的是从决策个体本身和其他决策者对该个体的评估两方面综合评判，使得决策者的权重并非固定不变，而是会随着决策者偏好的变化而变化。若某决策者对设计方案的认知一致性高，则偏好一致性的权重就高，反之则低。两种权重结合有助于避免决策者信任权重高但偏好矩阵一致性低带来的影响。

(3)群体决策的目的是降低单个决策者偏好偏离可能带来的决策风险，因此群体决策一般包括两个过程:共识过程与选择过程[27]。共识过程通过共识度模型测量群体对方案集合偏好意见的认同程度;选择过程是根据成员对方案的偏好，在满足共识条件下，通过集结算法获得最优方案。因此，共识达成是方案选择的基础，可通过群体讨论促进知识共享与意见交互、智能算法寻优调整偏好等方式促进共识。相对而言，群体讨论能够促进决策人员间对产品工业设计方案的总体认知，但对缺失偏好难以处理，且共识效果难以保证。而本文中的两阶段寻优能够快速实现共识达成，有助于提升产品开发效率。同时，共识阈值γ会直接影响优化轮次。在案例验证中，若将γ设定为0.85，则无需优化即可直接输出决策结果。一般根据实际情况，由决策协调者或者决策群体事先商定共识阈值[28]。

5 结束语

由于工业设计过程涉及工学、美学等多学科知识，产品方案的设计决策常呈现模糊性、感性与理性并存、多阶段性等特点，当决策人员面对多种设计方案进行优劣评判时可能出现犹豫，导致难以作出决策，从而造成偏好信息缺失。针对该问题，本文基于不完全互惠偏好关系的基本理论、运算规则与缺失偏好处理算法，融合决策人员偏好矩阵的一致性权重和信任权重，建立共识度模型判断决策群体意见的一致性程度，通过一致性权重比较确定待调整偏好位置，以共识阈值和偏好矩阵最小调整成本为目标，利用粒子群优化算法进行寻优，以促进决策者的共识达成并确定设计方案支配度，输出最优方案。基于以上研究，开发了软件原型系统，并结合实例进行了应用验证。下一步将研究产品工业设计过程的多阶段决策信息缺失问题与决策知识共享机制，进一步从产品开发全局角度提升设计决策质量。