多场环境下等截面结构性能分析及优化设计
2021-04-12柯庆镝李乾坤田亚明
柯庆镝,谢 敏+,李乾坤,田亚明
(1.合肥工业大学机械工程学院,安徽 合肥 230009;2.长虹美菱股份有限公司,安徽合肥,230601)
0 引言
为了满足当前社会不断迅速产生的多样化客户需求,在机械产品的结构设计中,其制造柔性化、高效率及低成本的要求愈来愈被重视,需要进一步针对机械产品中的传统结构及其制造工艺进行优化和升级替代。而等截面结构(例如型材、板材等)一般仅需要挤压、冷/热轧等成形工艺,具备模块化程度高、加工效率高、制备工艺成本低等特点,与传统铸造结构件相比,其制造周期与工艺成本均有一定程度的降低,因此,等截面结构件在现有机械装备中得到了大量应用。但对比传统铸造结构特性(如良好吸振性等),等截面结构零件往往需要进一步优化结构,同时伴随着轻量化和绿色化的需求,其自身的结构存在截面拓扑形态与其强度、质量等基本特性之间的冲突。针对结构截面的优化问题,国内外学者做了大量研究:吴凤和等[1]针对复杂载荷工况下横梁等大型三维结构件拓扑优化结果可读性差、无法对结构优化提供有效指导的问题,提出基于功能截面分解的拓扑优化方法。宋凯等[2]为了在概念设计阶段快速有效地实现车身梁截面的优化设计,提出一种基于P1N1(P1N-formed protein 1)植物生长算法的截面快速优化方法,通过提取出截面数据库中的截面节点坐标以及截面性能参数,将数据库中梁截面的节点坐标作为设计变量,导入PIN1植物生长优化算法中进行优化,从而控制梁截面的形状。周奇才等[3]为克服传统基结构设计方法对最优解的束缚,实现桁架结构的拓扑布局及尺寸优化,提出了将连续体与离散杆系相结合的桁架结构优化设计方法。马洪刚[4]在序列体各向同性材料惩罚模型
(Solid Isotropic Microstructures with Penalization,SIMP)插值方法基础上,提出一种从多材料拓扑优化到截面尺寸优化的两步客车骨架优化方法。Moucun等[5]针对太阳能集中器的设计介绍了一种变截面结构优化方法,这种设计主要的改进是在两端(扭矩箱结构处)保持梁的刚性和强度,同时允许结构中间相对较弱。Nguyen等[6]针对梁的长度方向上的离散化使用有限元法(Finite Element Method,FEM)对梁横截面进行屈曲拓扑优化,会增加较高的数值成本,而采用有限棱镜法(Finite Prism Method,FPM)作为线性屈曲分析的工具,借助于长度方向的谐波基函数,将FEM 的三维节点的自由度降低到二维节点的自由度。针对不同的梁长,解决了从矩形、L形和一般形状的设计域中寻找截面布局的优化问题。Grekavicius等[7]针对铝型材材料弹性模量低等固有缺陷,采用先进的结构拓扑优化技术,通过二维和三维相结合的方法,以后处理和可制造性为重点,提出了10种独特的截面轮廓。Kabanda等[8]针对加拿大目前使用的一种多边形空心结构钢截面进行数值优化。SUI等[9]为了提高框架结构的性能,对框架结构的截面形状进行了优化,使用分解技术分离两个变量,建立了框架结构截面和形状的两级优化方法。Li等[10]提出一种考虑制造约束的三维结构拓扑优化水平集方法。Liu等[11]研究了基于长度控制和几何特征的面向加工的拓扑优化设计,提出了面向注塑/铸造拓扑优化的零件顶出和肋厚度控制,指出了面向增材制造的拓扑优化方向。
通过以上研究,可以看到目前结构优化设计的研究主要是结合有限元分析方法,基于结构特性开展相应优化设计,计算过程复杂且需要相应的算法支撑,并且主要集中于结构强度优化,但结合其他类型需求(如轻量化、保温、降噪等)的综合考虑不足,缺乏面向多物理场服役的优化设计方法。而在大部分产品中,针对等截面为主的支撑结构,因结构工艺性限定,其设计范围主要是截面优化,需要一种高效且简单的优化设计判定方法,同时该结构均受到多物理场(温度、振动等)作用,需要满足多物理场内结构优化的设计需求。
针对以上问题,本文通过分析机械零件截面性能特性,提出基于惯性矩模型的机械零件结构截面优化方法:基于多场服役环境下性能需求,分析了零件等截面拓扑变化与其性能变化之间的映射关系,尤其针对其强度需求,建立了其截面结构惯性矩演化过程模型,提出了多场服役性能需求下零件等截面优化设计方法。结合某型号制冷产品门体结构零件的优化过程,验证了所提方法的有效性和适用性。
1 机械结构截面
等截面结构在工程中应用广泛,最常见的结构形式是机械装备中的支撑结构件,在航空航天、运载机械、工程机械等领域,很多结构件都可以简化为不同类型的等截面结构。这些机械零件是其机械产品的重要结构组成零件,用于连接与支撑其余重要零部件,如控制、执行、动力等,承受着机械产品使用中的绝大部分载荷及冲击,其自身结构设计不仅需要考虑产品空间尺寸需求,更需要分析其结构在产品运行载荷谱及冲击下的强度问题。并且,再进一步结合产品服役环境,也需要分析轻量化下结构质量约束,以及运行过程中的结构振动、热传导等性能,这些因素均会限制乃至损坏产品结构安全性和相关零部件功能有效性,也使得整个设计环节更为复杂。因此,在机械零件等截面结构设计中,需要详细分析其截面拓扑所体现的不同性能(包括强度、质量、热导性等),以满足产品各类工作载荷及性能需求。
1.1 零件结构截面建模
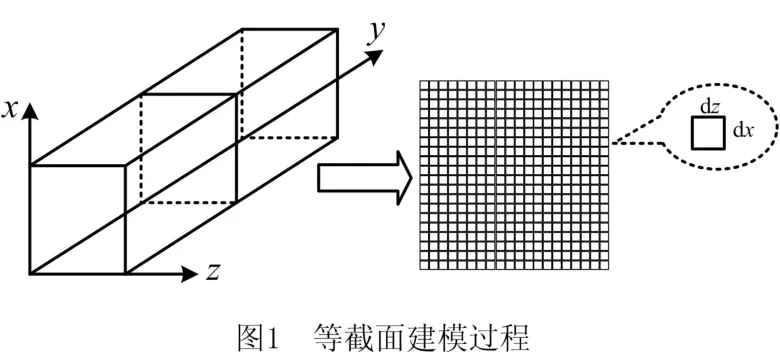
由于机械零件中等截面结构的基本尺寸源自于产品框架结构设计需求,其产品功能参数一定的情况下,其基本框架结构尺寸一定。大多数情况下,等截面零部件的支撑结构在其截面纵向上的尺寸受产品功能参数限制,优化范围较小。因此,结合等截面设计特性,将等截面结构零件中截面特征提取出来(如图1),构建其二维截面量化描述:
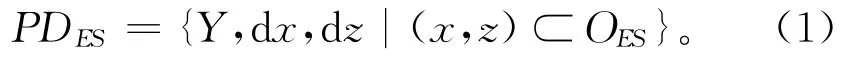
式中:PDES表示等截面结构零件的设计方案;Y表示等截面结构零件在截面垂直方向上的长度设计需求;dx表示截面在x方向的微分量;dz表示截面在z方向的微分量,OES表示截面微分单元在平面上的位置集合。
基于式(1),可将等截面零部件的结构从传统三维模型简化为二维截面,同时结合微分分析方法,构建截面微分单元的不同性能特征(如强度、质量、模态等),并结合截面设计方案,获得该等截面零部件的基本性能。例如,等截面零部件的质量可表达为:
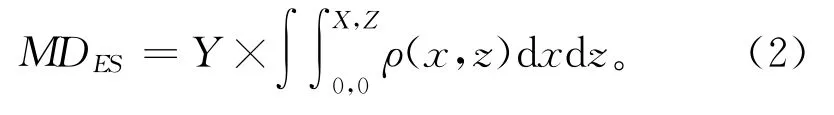
式中:MDES表示等截面结构零件的整体质量;ρ(x,z)表示随截面位置(x,z)变化的截面密度函数。
通过构建截面的不同性能函数,获得等截面零部件的各类性能描述。同时在分析零部件各类性能需求的基础上,可以进一步开展相关的优化设计。
1.2 结构性能分析
如前文所述,在等截面结构设计中,需要综合考虑并满足其各类性能需求及约束。这样一来,就需要结合等截面结构模型,分析并构建其结构性能表达函数。具体如下:
(1)强度性能
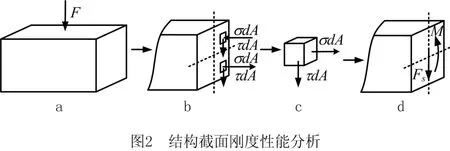
在工程实际应用中,基于零部件的不同功能,其等截面结构所受外载荷类型也有所不同,可能单纯受集中力、均布载荷、不均布载荷或力矩作用,也可能受上述载荷的综合作用,且各类载荷的作用时间段也会有区别。在外载荷的作用下,零部件结构内部会产生应力,进而发生弹性变形,直至其屈服乃至断裂。因此,外载荷作用下内力分布场是分析等截面结构强度的基础,在应力场下各个截面微分单元所产生的应变,构成了等截面结构整体变形分布(如图1),可表示为:
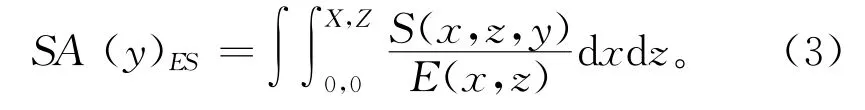
式中:SA(y)ES表示等截面结构零件的在长度y处的变形;S(x,z,y)表示在长度y处,随截面位置(x,z)变化的应力函数;E(x,z)表示随截面位置(x,z)变化的刚度函数。
图2a表示结构受力示意图,图2b表示结构任一截面微分单元受力示意图,图2c表示截面任一微分单元模型受力情况,图2d表示结构任一截面受力示意图。
(2)热传导性能
机械产品在某些温度场工作环境中,需要保障其内部零部件的有效性能和可靠性,则对起框架支撑作用的等截面结构类零件,要求其具备一定保温或散热性能,这样就需要分析零部件结构的传导性能,可以表达为:
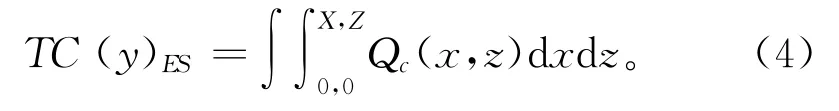
式中:TC(y)ES表示等截面结构零件在y方向的微分单元传热量分布;Qc(x,z)表示随截面位置(x,z)变化的结构传热量函数。
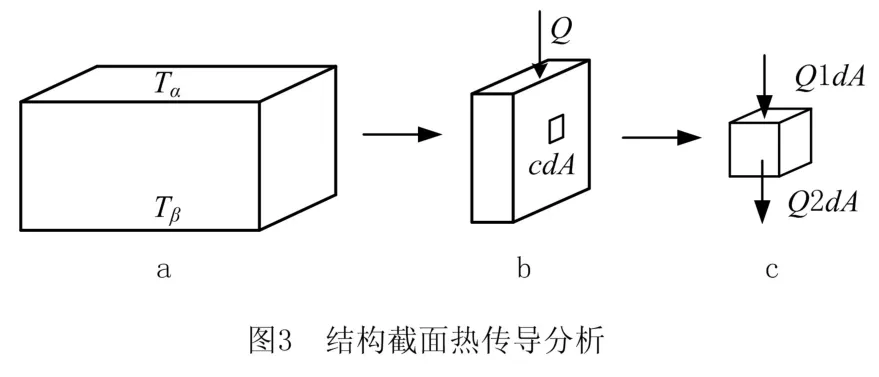
基于式(4),通过分析结构零部件所服役的温度场环境,可以获取其热分布状态,进而对照设计需求不断优化结构的热传导性能(如图3)。
图3a表示结构所处环境温差示意图,其中Tα≠Tβ;图3b表示结构任一截面微分单元示意图,其中Q表示结构传热量;图3c表示任一截面的某微分单元模型的热传导分析。
(3)其他性能需求
在产品中占主要体积构成的结构零件,其材料占比高、制造成本高,随着目前产品轻量化、低成本的需求不断加强,此类结构类零件是主要的结构设计优化对象。基于所构建结构截面模型,可以得到其质量分布:
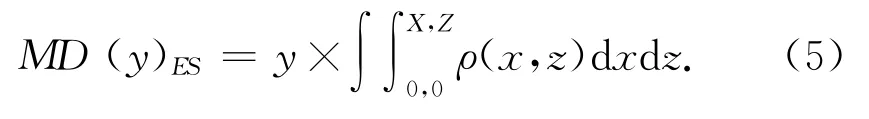
式中:MD(y)ES表示等截面结构零件在长度y处的质量分布。
同时,在获得材料分布的基础上,该零部件的制造成本分布如下:
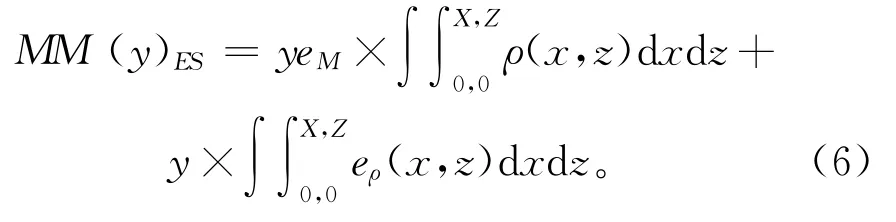
式中:MM(y)ES表示等截面结构零件在长度y处的制造成本分布;eM表示面积单元的材料成本;eρ(x,z)表示随截面位置(x,z)变化的结构工艺成本函数。
1.3 截面强度与惯性矩
如前文所述,强度性能是等截面结构设计中考虑的首要因素,而基于上述分析,结构截面刚度分布是其关键参数,大多数研究均从这一点入手,但截面刚度及其变形的计算过程较为繁琐,且随着截面几何形状变化,会产生较大的差异性,导致整个分析优化过程复杂。一般来说,需要在分析截面结构的基础上计算截面结构刚度[12],具体如下:
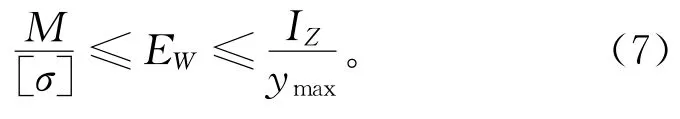
式中:[σ]表示截面材料屈服应力;M表示结构截面上弯矩载荷;EW表示截面抗弯刚度;ymax表示截面离中心轴最大变形,IZ表示截面的惯性矩。
由式7可知,在一定的工作负载(M)下,结构截面刚度需求受其零件材料特性(屈服强度[σ])的影响。同时,截面刚度(EW)与其惯性矩(IZ)成正比,与截面结构变形(ymax)成反比。因此,惯性矩可被视为结构刚度分析环节中关键物理量,可以直接反映出该截面刚度的大小,其计算[10]过程如下:先确定该截面的中性轴(或形心轴)位置(如图4),后基于所得到中性轴计算惯性矩(如式(8)~式(10))。
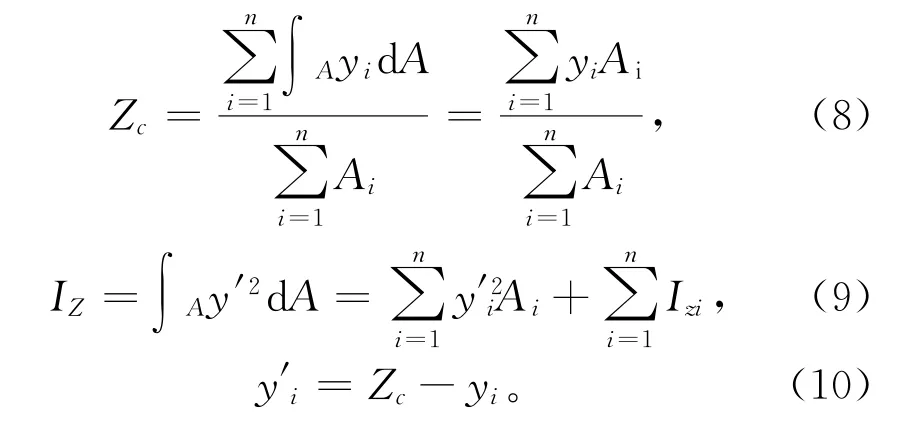
式中:Zc表示中性轴位置;yi表示微分块到坐标轴距离;Ai表示微分块面积;IZ表示截面的惯性矩;yi'表示微分块到中性轴的距离;Izi表示微分块相对于自身惯性矩。
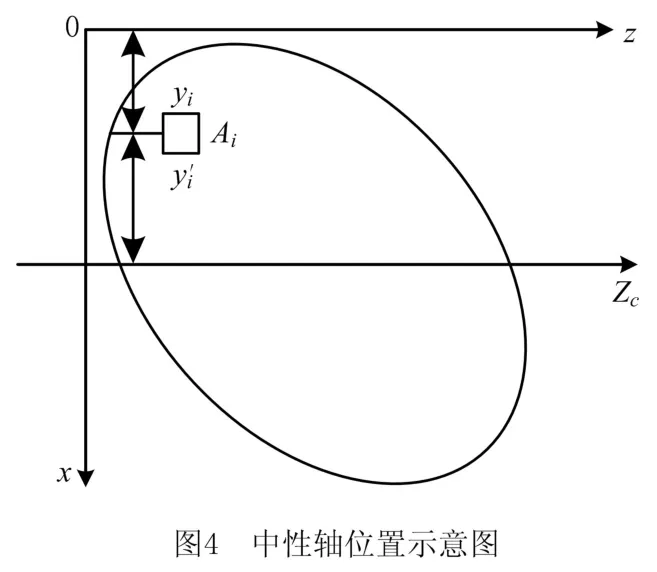
从式(7)~式(10)可以看出,在结构截面拓扑形状一定的前提下,能够进一步确定其惯性矩及结构刚度,且其计算过程较为简便。因此,在优化零部件结构刚度时,可以将截面惯性矩视为其直接优化目标,进而间接提升整体结构截面刚度。同时,针对不同方向的刚度需求(如轴向、切向等),结合前文构建的结构截面模型,可以得到其中性轴和惯性矩表达如下:
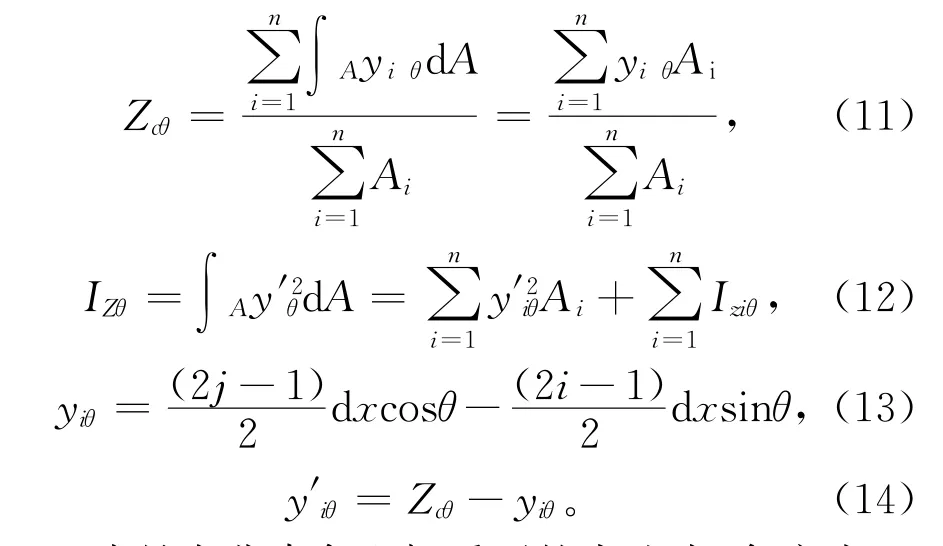
上式是在非直角坐标系下的表达式,角度为θ;i、j分别为微分单元所在行、列;dx、dz分别为微分块的在x、z方向的长度。
基于式(11)~式(14),通过分析比较在整个优化过程中的各类截面几何形状下惯性矩大小,选择具有较大惯性矩的截面拓扑形状作为截面优化的参考集合,进而可以得到具有良好截面刚度的优化结构。
2 等截面结构性能分析及优化方法
基于前文的结构截面模型及性能需求分析,可以进一步研究等截面结构的优化问题。首先应对不同结构的截面拓扑改变过程进行量化描述,同时分析在该截面拓扑演化过程中结构性能的变化规律,构建其相应的函数表达。在其各类性能设计要求基础上,构建其量化性能约束表达,并提出其相应的结构截面优化方法。
2.1 等截面结构拓扑演变过程
一般来说,结构截面演化可被视为其截面在二维平面中几何形状及轮廓的变化,结合所构建的结构截面模型,结构截面可被定义为在二维平面中有限数量的微分单元的集合,即平面中不同区域的微分单元构成了结构截面整体。基于式(15),得到不同结构的截面拓扑形状可被不同位置的微分单元集合表达,即
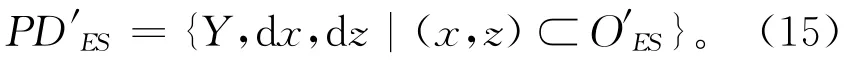
可以得到,优化后结构截面可以被视为在原始结构截面基础上的微分单元集合修正,即通过对不同区域微分单元的添加或删减,实现对整个结构截面上各类性能的优化。为便于过程描述及操作,可以设定截面拓扑变化按步进方式进行,即每次均减少或增加一个微分单元,以便分析微分单元变化所带来的等截面结构性能影响。
2.2 等截面结构性能演化函数
为了分析在结构截面拓扑演化过程中各类结构性能的变化规律,需要设定截面拓扑的变化过程。为便于计算,可以假定原始截面形状为最大量值的微分单元集合,即截面形状为最大设计范围,在后续拓扑变化中需要不断地删减在不同位置处的微分单元,而在这一去除微分单元过程中,分析其结构性能变化规律,可表示为:
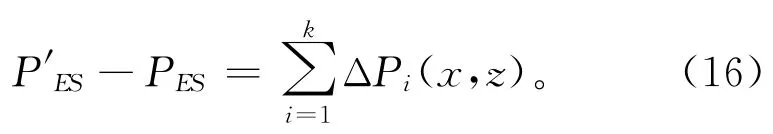
式中:P'ES、PES分别为优化后及原始截面拓扑形状下的结构性能;ΔPi为第i次去除位于(x,z)位置处的微分单元时结构性能变化。
这样一来,可以通过分析结构性能的变化量,在考虑设计需求的前提下,寻找在性能变化量极限值下的微分单元删除位置,而后依据删除位置标记,得到其相应结构截面拓扑描述,进而获得满足设计要求的最佳结构截面。
(1)强度性能
基于所构建的惯性矩模型式(11)~式(14),可以计算得到结构截面,在去除(i1,j1)处微分单元之后的中性轴位置和截面惯性矩表达式(17)和式(18):
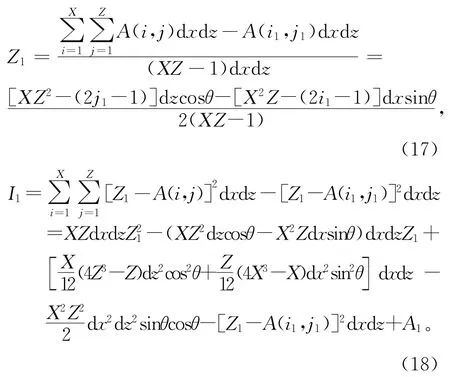
在去除(i2,j2)处微分单元之后的中性轴位置和截面惯性矩表达式为
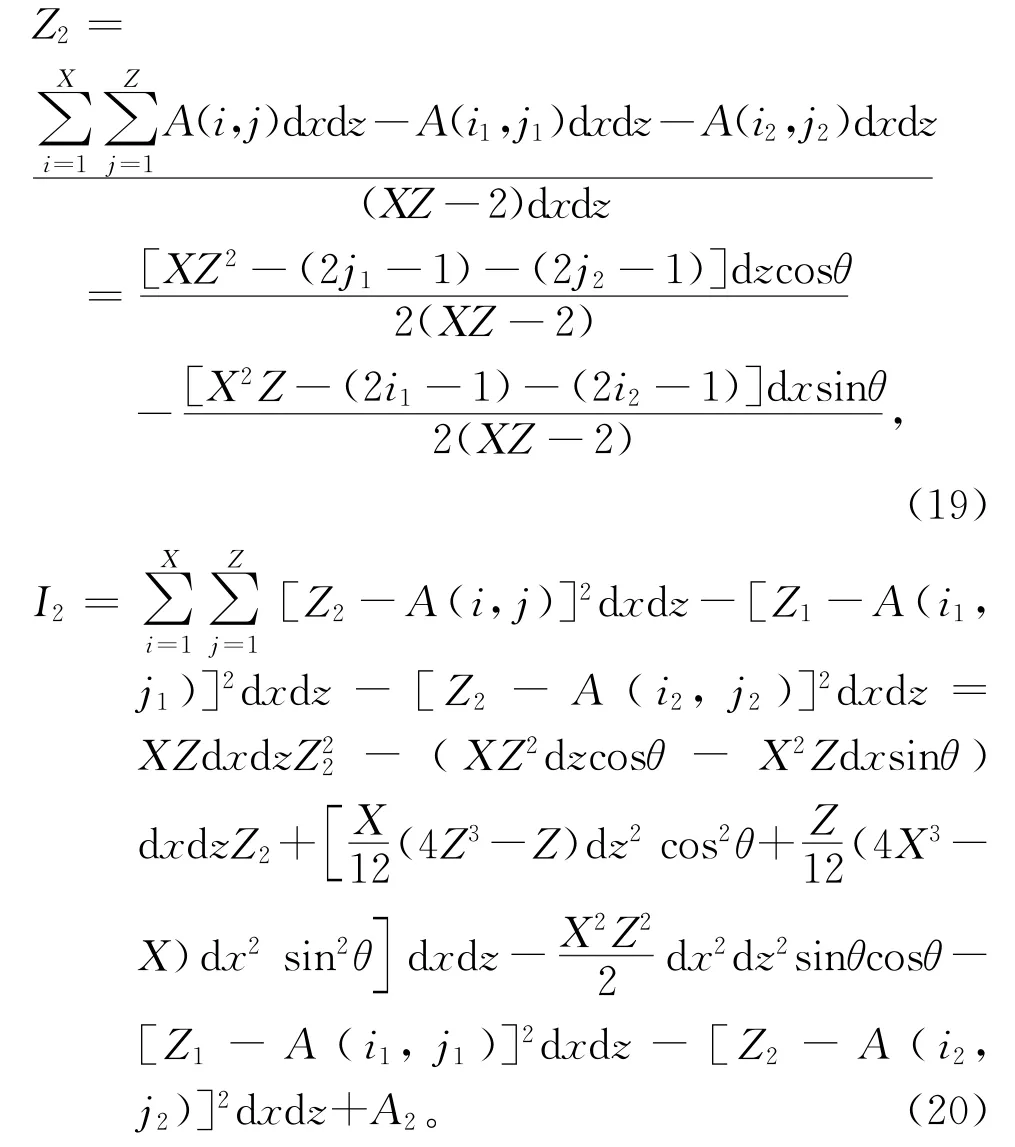
由上面规律可得去除(ik,jk)处微分单元之后的中性轴位置和截面惯性矩表达式(21)和式(22):
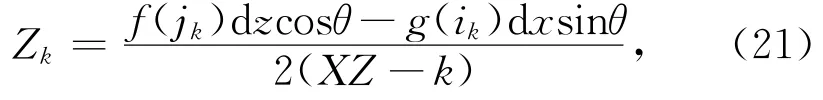
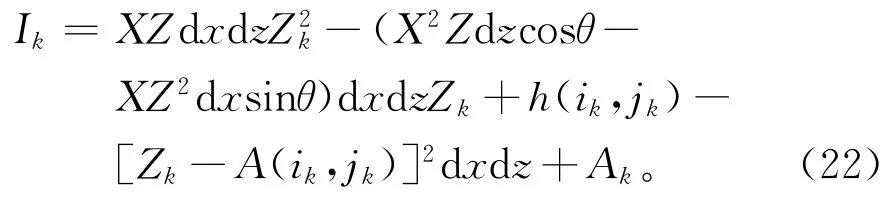
式(21)为坐标系在θ角度下,结构截面在删减(ik,jk)处微分单元之后结构截面中性轴位置表达式;式(22)为结构截面在删减(i,j)处微分单元之后结构截面的惯性矩表达式,当θ=0,即直角坐标系下,Ak=(XZ-k),是定值,在非直角坐标系下,Ak是与θ、k相关的表达式,在优化过程中,每步的θ、k是常值,所以在非直角坐标系下Ak为定值。
其中:
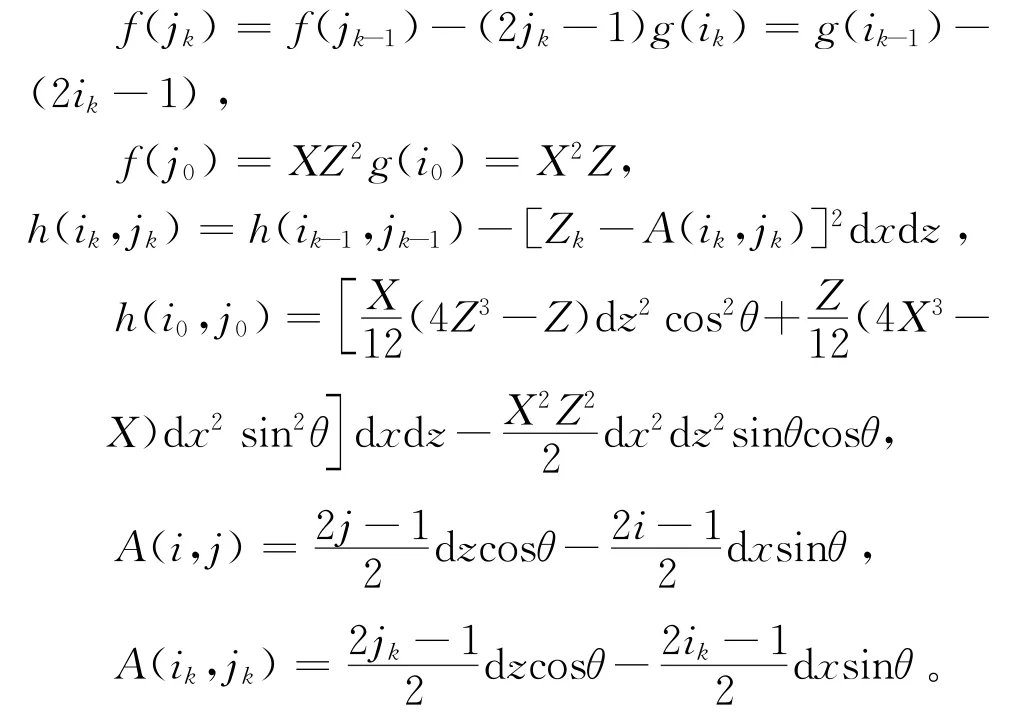
式中:X表示结构截面在x方向上微分单元的总行数;Z表示结构截面在z方向上微分单元的总行数;i表示某微分单元位置在x方向上第i行;j表示某微分单元位置在z方向上的第j行;f(jk)为j的迭代表达式,g(ik)为i的迭代表达式;h(ik,jk)表示i、j的迭代表达式。
基于以上公式,可以得到微分单元的量值与其结构截面惯性矩成正比关系,在不断删减微分单元的时候,为了降低其对截面惯性矩的影响,需要选取在惯性矩最小减少量处(k)的微分单元位置,以期获得相同条件下最好的结构截面刚度性能。删减的微分单元在下一次优化中不被恢复。
(2)热传导性能
结合所提出的热传导性能表达式(如式(23)),可以得到去除(x,z)处微分单元的结构截面传热特性变化:
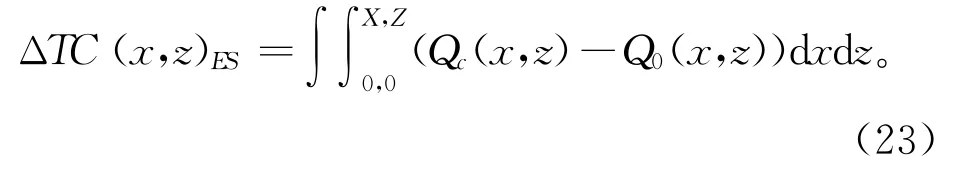
式中Q0(x,z)为在去除(x,z)处微分单元后该空间的传热量函数。
基于企业调研,大多数情况下将热传导性能视作设计约束,即设定热传导性能阈值,或者为保障其具备一定的温度特性,直接设定微分单元的位置范围阈值。比如,当需要散热性能时,可设定某些传热位置处微分单元不可去除,即
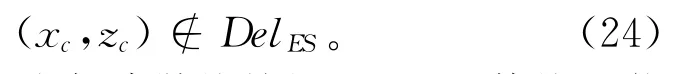
式中:(xc,zc)为在保障散热特性下,用于传热的截面微分单元位置集合;DelES为可去除的截面微分单元位置集合。
(3)轻量化性能
伴随着结构截面上微分单元的去除,其截面质量不断减少,并且每一步去除的减少量是该微分单元质量,可表示为
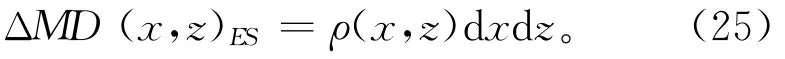
同样,在结构优化设计中,将轻量化性能转化为设计指标约束时,可表示为
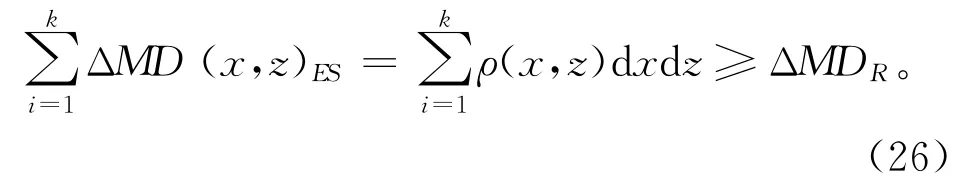
式中ΔMDR为结构设计时制定的轻量化阈值,即最少的质量减轻值。
2.3 优化模型对比
基于前期调研,现有拓扑数学优化模型可表达为[13]:
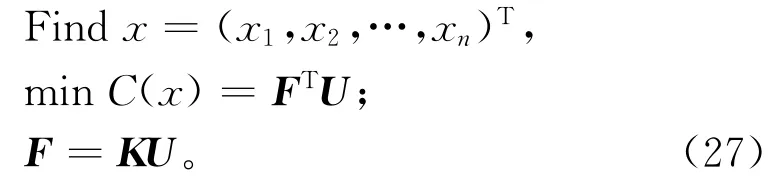
其中:xn为设计变量,n代表设计变量个数,F为结构所受的外力向量,U为结构的位移向量,K为总刚度阵。
与本文所提优化数学模型的对比如表1所示。

表1 拓扑模型和本模型对比
拓扑模型以位移最小为优化目标,本文以结构惯性矩I最大为优化目标,与位移或结构柔顺度最小相比,惯性矩最大是一个优化过程的中间量,从而可以减小优化工作量,同样能达到优化目的。
其计算次数对比图如图5所示。
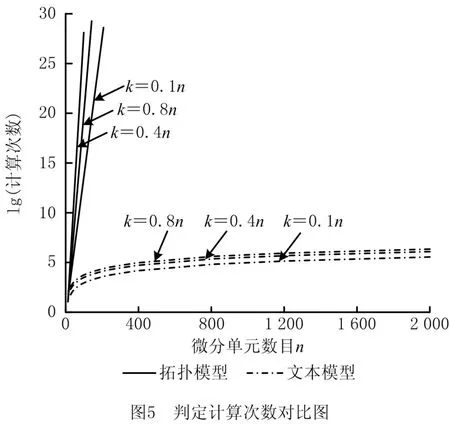
如图5所示,现有拓扑优化模型和本文所提出的优化模型的判定计算次数均随微分单元数目(n)增加而上升,对于现有拓扑优化模型,其判定计算次数增长速率较大,且在微分单元数n=100左右时就超过了1025,即“组合爆炸”,从而需要相应的算法优化。另一方面,本文所提方法的判定计算次数的增长速率是不断减小的,且在微分单元数n>103以上时,判定计算次数的增长逐渐平缓。这样,针对等截面结构优化,尤其是微分单元数量较大时,本文所提方法的判定过程优于传统的拓扑模型。
2.4 优化设计方法
基于上述的结构截面拓扑演化过程及其结构性能演化规律分析,可以结合惯性矩模型,针对当前的等截面结构优化设计问题,提出相应优化模型与设计方法,具体步骤如下:
(1)构建目标函数
分析等截面结构优化设计的多类性能需求,构建各类需求的量化表达式,将主要设计需求(如结构刚度等)设定为目标函数,如有多个主要设计需求(如结构刚度与保温性能等),则需要通过定制标准化系数[14-15](如专家法、功效系数等)将多个主要设计需求标准且统一为单一函数,设定其为目标函数。
(2)提出约束函数
在构建目标函数后,将其余性能设计需求(如轻量化需求等)设定为约束函数,结合其设计需求极限范围,设定相应设计约束函数的阈值(如最少质量降低值等),进而构建完整的设计约束函数表达。
(3)构造优化模型
优化模型包括优化目标和优化约束,构建的优化模型一般形式如式(27)所示,本文的优化模型如式(28)。
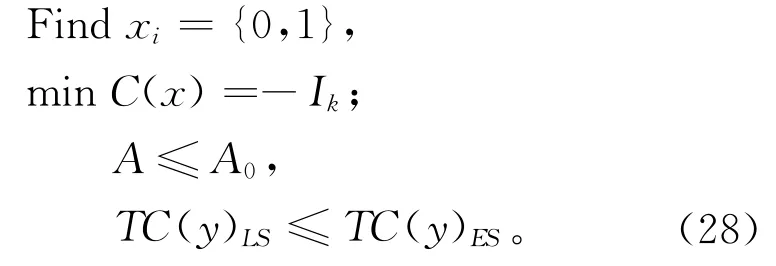
式中:xi为优化对象为微分单元(xi),取值为0(去除)或1(保留);目标函数则为拓扑结构惯性矩最大值,即minC(x)=-Ik;约束函数则设定为结构优化中其余方面设计需求,基于前文论述,轻量化需求下约束函数可用优化前后的截面横截面积之比(A)表示;同时,结构传热需求下约束函数,可用TC(y)LS≤TC(y)ES表达。
(4)优化结果验证
在获得结构优化结果后,可结合结构截面的各类性能函数,分析其各类性能是否满足相关设计需求,如满足,则可设定其为结构优化设计方案,并可借助模拟仿真或实验开展进一步分析,以验证其结构优化方案的有效性。
3 案例分析及验证
3.1 研究对象设定
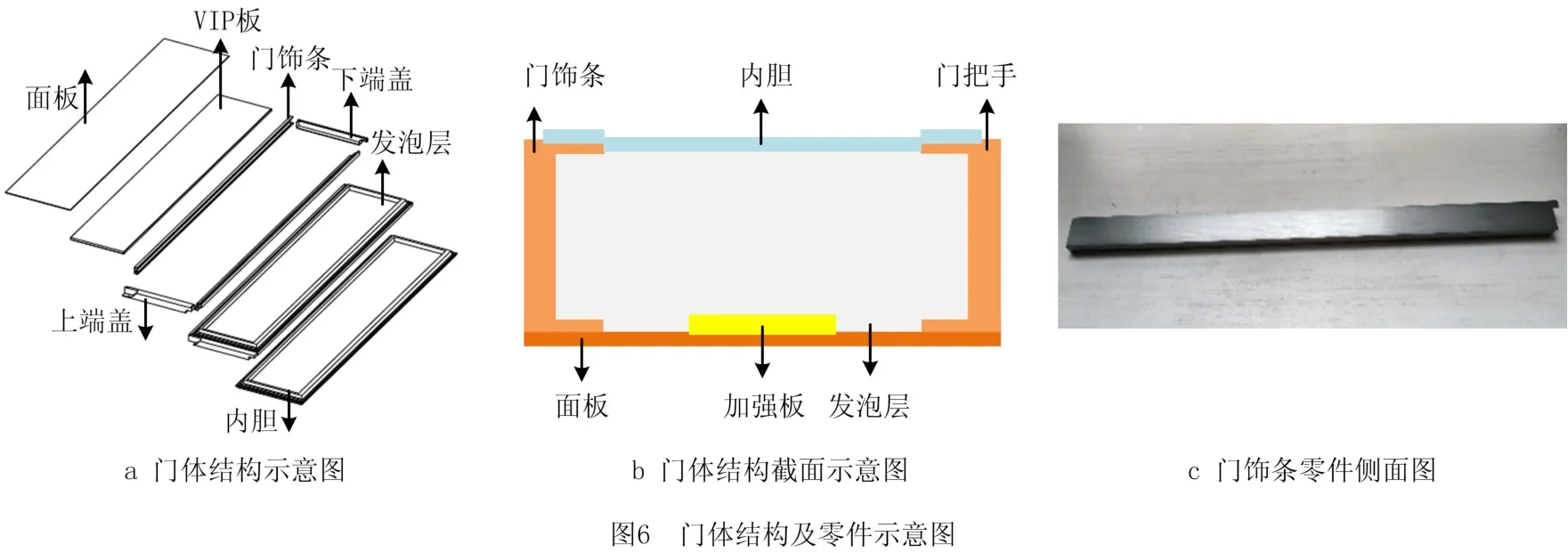
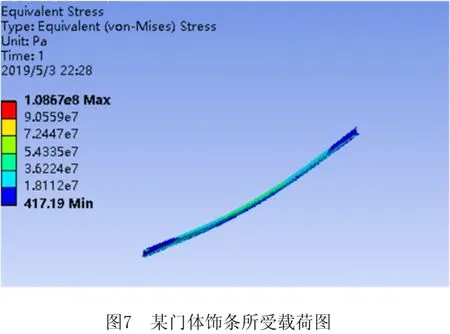
本文所用案例来源于某公司的某型号制冷产品门体饰条。该制冷产品门体结构中,门饰条分布在门体的侧边,是一个等截面的支撑结构,也是门体的重要组成部分。该制冷产品门饰条既受温度场又受力场的作用,在复合场下门饰条会产生形变。门饰条的变形过大会使门体产生翘曲,使该制冷产品密封性下降,影响其正常使用性能,一些研究均表明门饰条优化对改善门体强度有显著作用。如图6所示为某型号制冷产品门体截面装配示意图和爆炸示意图,如图7所示为某制冷产品门体饰条所受载荷。可看出其所受应力大体分布趋势,门饰条中部所受应力最大,从中部往两端逐渐变小,两端受力最小。如表2所示为门体饰条优化设计参数。
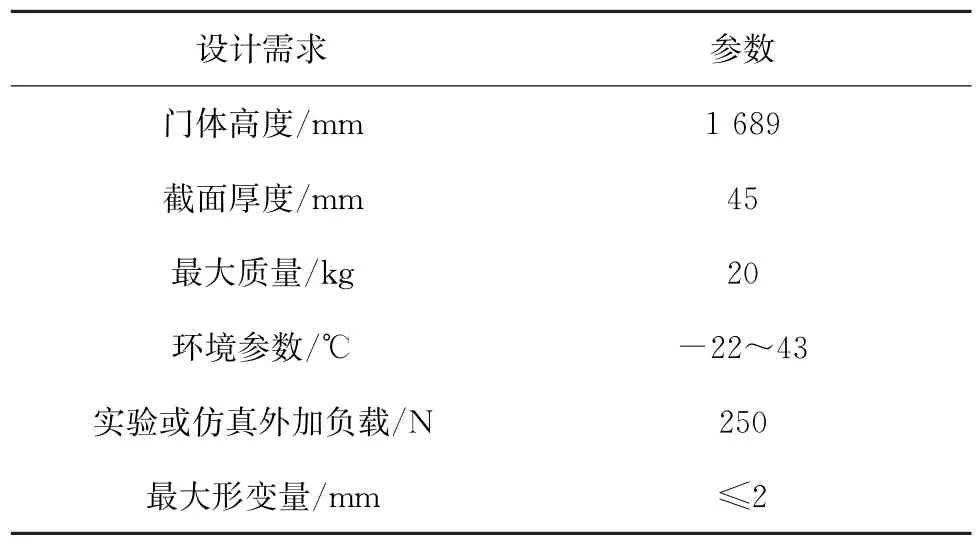
表2 结构参数和环境参数
3.2 优化分析过程
通过前文所述的优化设计方法,完成对某型号制冷产品门饰条的优化。
(1)构建目标函数
本文优化目标函数为删除惯性矩最小的微分单元,使得最终拓扑结构的惯性矩取得最大值。
(2)提出约束函数
基于轻量化需求,构建质量约束函数:
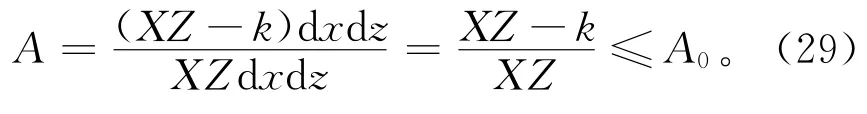
式中:A表示优化后截面面积与设计区域截面面积之比;A0表示优化前截面面积与设计区域截面面积之比;k表示去除的微分单元数量。
对门体保温性能需求,需要构建与保温特性相关的约束函数。对于等截面结构(如图1),其y方向的微分单元传递的热量为
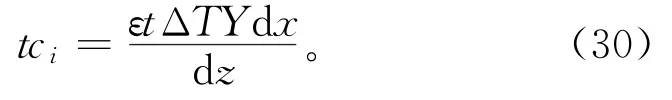
式中:tci表示微分单元i传递的热量;ε表示微分单元i部分的热传导系数;A表示传热面积;ΔT表示温差;t表示热传导时间;Y表示门饰条长度。
基于保温性能需求,且温差(ΔT),时间(t)以及门饰条长度(Y)在结构优化中为常数,则构建传热量约束函数:
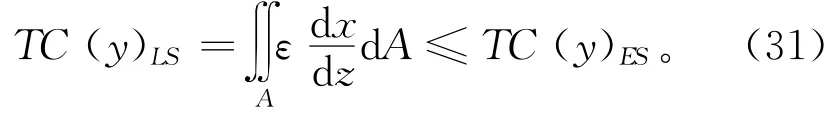
式中:TC(y)ES,TC(y)LS表示优化前/后结构传热量。门饰条结构包含两部分:铝合金材料的热导系数εl=209 W/(m·k),空气的热导系数为εk=0.024 W/(m·k)。
(3)优化过程
令dz=0.5 mm、dx=0.5 mm、X=76、Z=7、θ=0.62。将以上参数代入式(21)和式(22),按以下流程图(如图8)编程计算出满足目标函数的微分单元的位置,直至满足约束函数。优化模型求解是在编程分析软件VS2008上完成,优化模型计算耗时根据优化结构的复杂程度、微分单元精度、微分单元划分方法等因素有关,在本文所展示实例设定下,该模型计算373次。
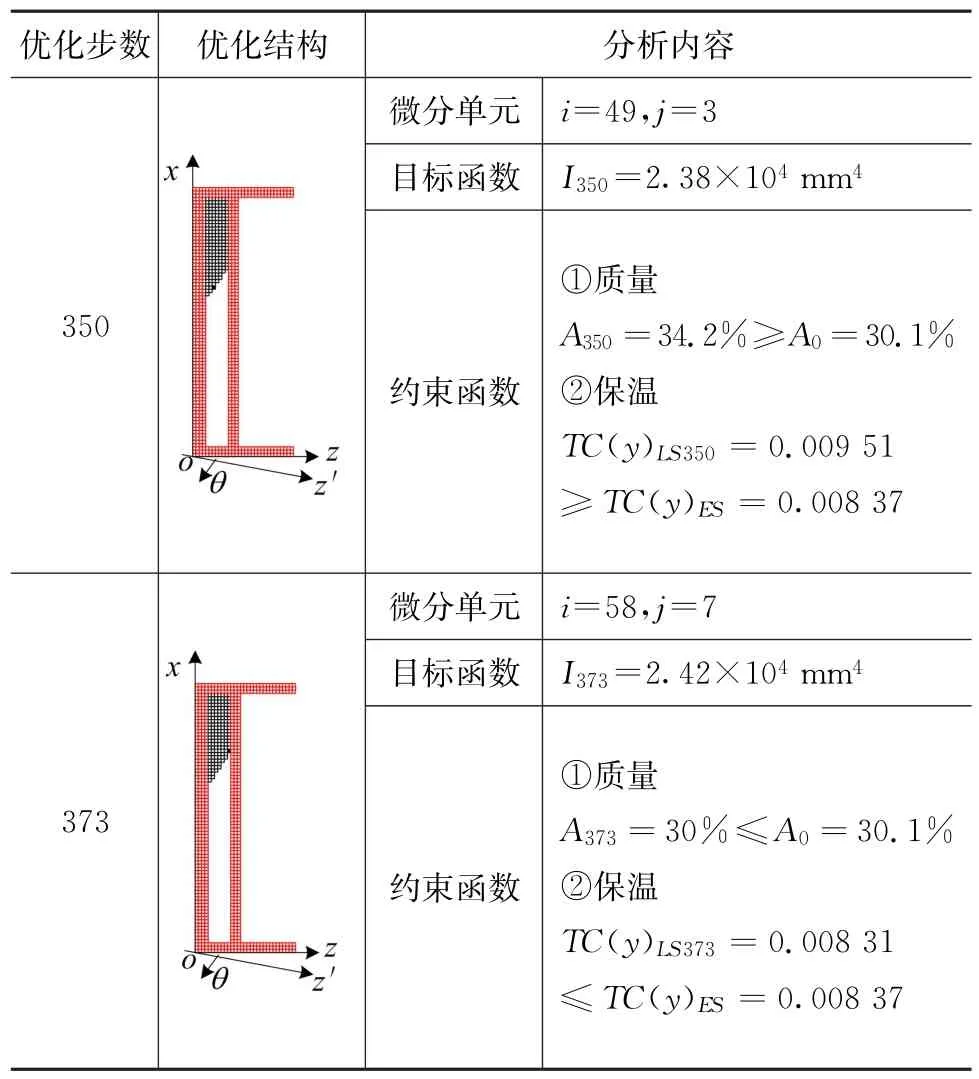
本文将上述制冷产品门体饰条作为优化原始模型,进行截面建模,浅灰色区域为非设计区域,在优化过程中保持其外部几何形状不变,中间的黑色微分单元构成的区域为设计区域,也即本文的研究对象(如图9)。最终结果如图10所示,优化过程如表3所示。
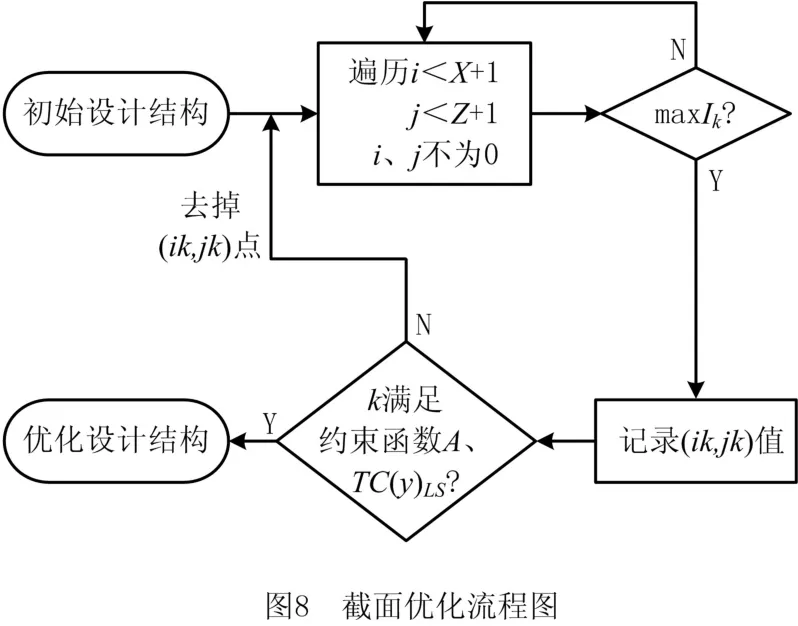
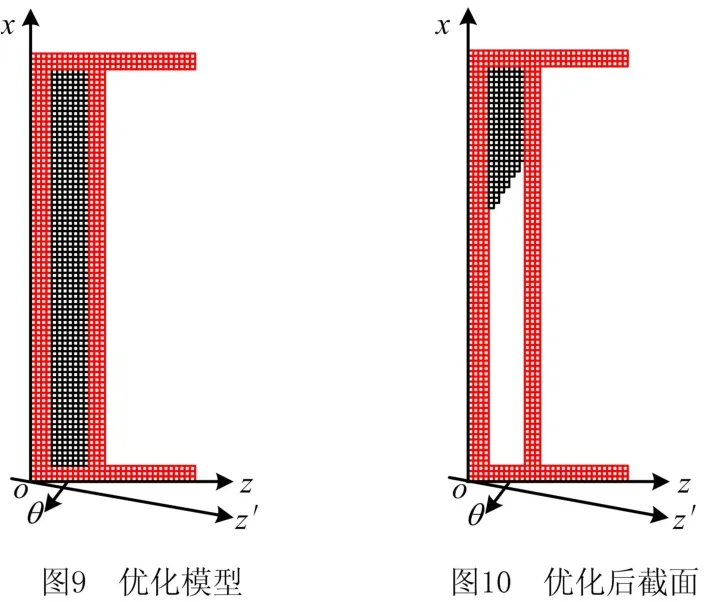
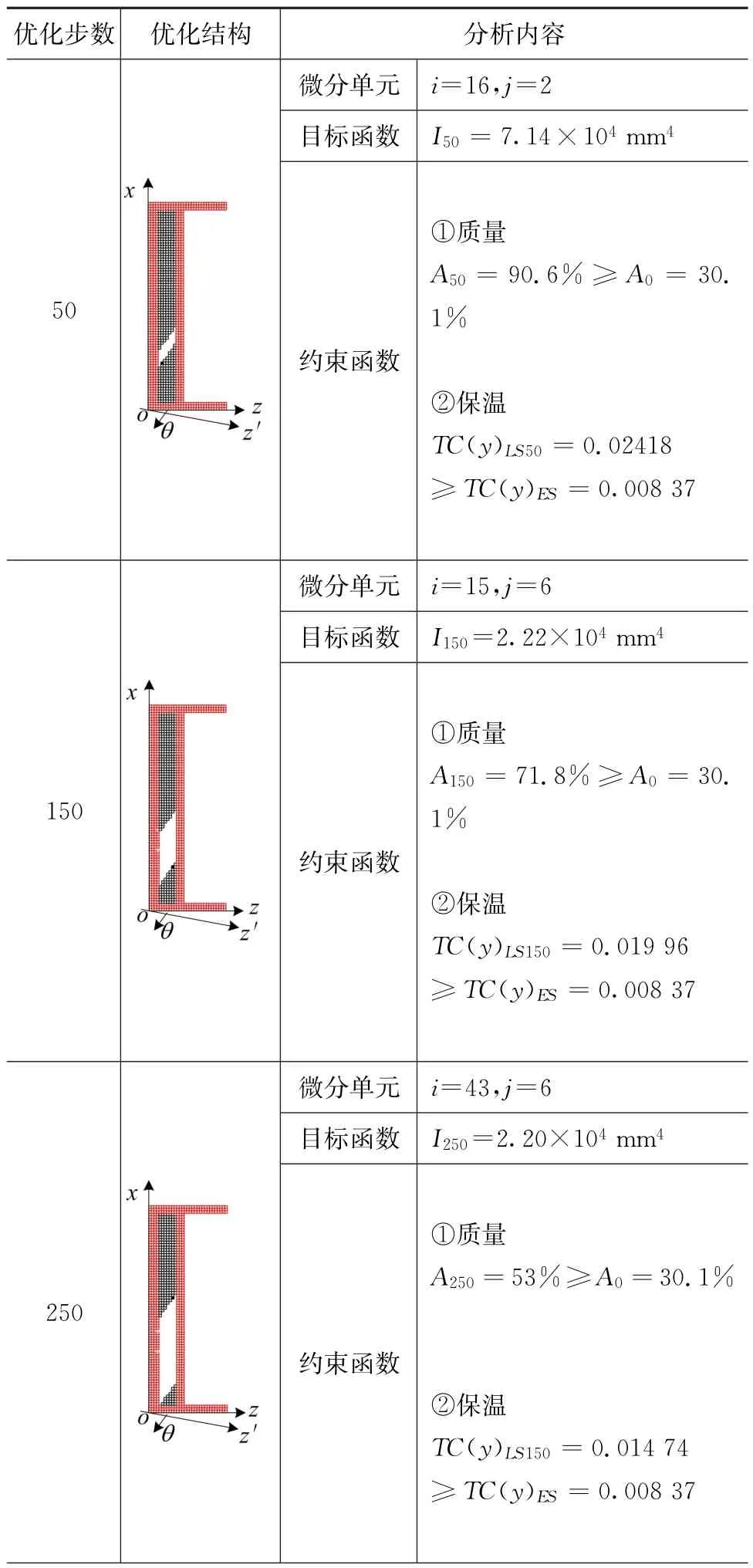
表3 优化过程
续表
3.3 结果与验证
优化后门饰条截面微分单元分布如图10所示。将优化结果三维建模如图11,优化前门饰条模型如图12所示。用优化后门饰条模型取代优化前门饰条模型新建一门体,将优化后门体与优化前门体均导入结构分析软件,模拟其真实工作情况—在温度场和力场共同作用下,得到门体整体和门饰条变形情况,如图13~图16,以上结果可总结如表4所示。



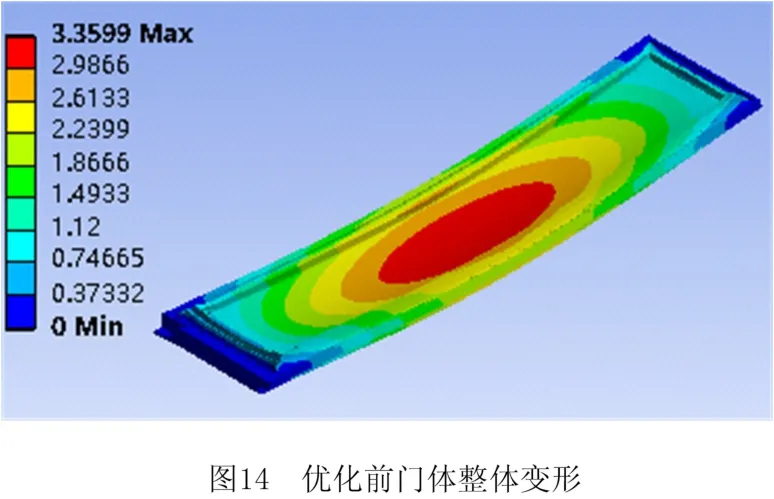


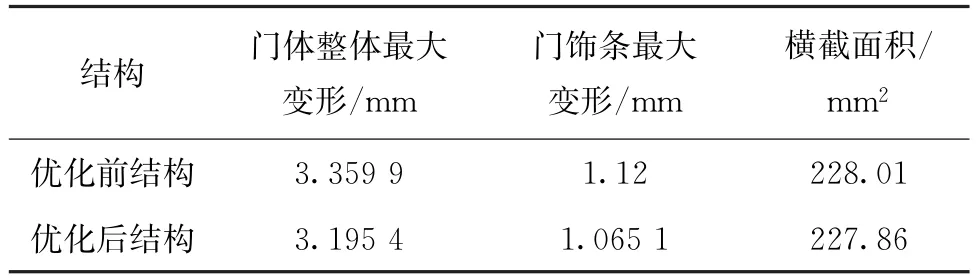
表4 结果对比
可以看出,在优化后门饰条结构横截面积比优化前门饰条结构横截面积小0.15 mm2,满足A≤A0。
对于保温性能需求,根据优化过程第373 步可得:
TC(y)LS373=0.008 31≤TC(y)ES=0.008 37,优化后结构的传热能力比优化前的结构弱,满足TC(y)LS≤TC(y)ES。
且门体整体最大变形优化后结构比优化前结构减少约4.9%,门饰条最大变形优化后结构比优化前结构减少约5%。
上述结果表明,本文所用从惯性矩角度出发解决等截面结构优化问题的方法切实可行,可以合理分布设计区域的微分单元位置、增强设计截面刚度、减小形变。从提升产品绿色性角度,每台门饰条横截面积减小0.15 mm2,且该类产品年度零售量约250万台,年节约材料约1.68 t,节约能耗约7358.4 kW·h。
4 结束语
本文面向产品多场服役下性能需求,提出一种结构优化设计方法:
(1)针对产品服役过程中各类物理场中的性能需求,结合等截面结构特性及有限元分析方法,构建了零件等截面模型及各类性能表达。
(2)面向不同服役环境下性能需求,分析了零件等截面拓扑变化与其性能变化之间的映射关系,并结合强度分析建立了截面结构惯性矩演化过程模型,提出了基于微分单元的零件等截面优化设计方法。
(3)以某制冷类产品的门体饰条零件为分析对象,分析其服役环境中的各项性能需求,并优化其截面结构,结果表明优化后截面结构刚度增加,形变减小,验证了本文所提出方法的可行性。
本文所提出基于微分单元的零件等截面优化设计方法,可应用于机电产品典型零部件中等截面结构的优化设计,具有一定的普适性,但结构不同性能属性表达、多场环境下零件结构不同性能之间耦合关系、截面优化迭代算法等问题有待后续进一步研究。
