基于激光测距的大部件对接方法及误差分析

秦 宇，黄 翔+，邓正平，陈允全，主 逵

(1.南京航空航天大学机电学院，江苏 南京 210016;2.中航工业成都飞机工业(集团)有限公司产品研制部，四川 成都 610091;3.深圳市劲拓自动化设备有限公司，广东 深圳 518000)

0 引言

大部件对接是一项技术难度大、涉及学科领域多的综合性集成技术，其很大程度上决定了飞机装配的最终质量与制造周期。随着大尺寸测量系统及自动定位技术的快速发展，大型部件的自动对接已经被广泛研究[1]。其中数控定位器用来支撑和调整组件的位姿，激光跟踪仪、激光雷达和iGPS等通过测量组件上的关键特征点来检验位姿的准确性。陈良杰等[2]针对将iGPS引入飞机部件对接环节所引起的问题，采用基于罗德里格斯矩阵的坐标系转换算法，实现iGPS测量坐标系和设计坐标系的统一，采用基于加权单位四元数的位姿比对技术，解算调姿驱动点的当前坐标值，然后采用“三点调姿法”，根据调姿驱动点的当前坐标值与理论坐标值关系规划部件调姿轨迹，解算调姿定位器各驱动轴的增量，最后以ARJ21翼身对接作为应用实例，验证了系统各关键技术解决算法的可行性[1]。屈亚伟[3]提出了基于激光跟踪仪的飞机位姿测量方案及基于共轭梯度法的飞机位姿解算方法，并对解算方法的误差进行了分析和实验验证。张奎生[4]介绍了飞机产品装配工装的生产制造、现场安装调试，并结合一定的飞机装配实例展示激光跟踪仪系统的技术应用[4]。这些对接系统以及有效的算法通常可以确保部件间的高精度的对齐，但在复杂环境下，大尺寸测量装置易受温度、气流等非稳定性因素影响，装配精度难以保证。已有大量研究将视觉测量应用于大部件检测与对接中[5-8]，但在机器视觉系统中，光源直接影响输入数据的质量，也影响了至少30%的应用效果。由于没有通用的机器视觉照明设备，所以需要针对每个特定的应用实例选择相应的照明装置。常见的数字化测量设备如iGPS、激光跟踪仪、视觉测量系统、激光测距传感器测量等，已在航空制造企业投入使用[9-10]。iGPS 系统精度可达到0.12 mm(10 m)～0.25 mm(40 m)，其测量范围广，不受温度影响，可根据需要确定测量坐标系的位置，但其精度相对较低，设备需手动标定不便于实施自动测量和布设测量站位。激光跟踪仪系统精度可达15μm+6μm/m，站位布设较为灵活，测量精度相对较高，可自动追踪测量，但是需要人工手持靶球引光，对员工技能要求高，且易断光，精度易受外界环境影响;视觉测量精度可以达到微米级别，且不易受到环境影响，智能化程度高，目前多基于靶标特征进行测量，测量准备工作繁重;激光测距传感器(西门子HG-C系列)精度可达到10μm(30 mm)～200μm(200 mm)，属于非接触式测量，其抗干扰能力强且隐蔽性好，因此应用广泛[11]。本文提出一种基于激光测距的大部件对接方法与装置，能够快速安装与拆卸，实现部件的调姿，并且能够达到较高的装配精度。

大部件对接中的关键技术包括调姿系统设计[12-16]、对接测量技术、调姿轨迹规划[17-18]、对接质量评估[19]、部件位姿估计[20]、调姿系统误差分析等。郭洪杰[16]结合某型机大部件对接的工程实际应用，对数字量协调的工艺设计、面向飞机装配的数字化测量技术、柔性工装结构设计和系统集成控制管理进行了深入研究;朱绪胜等[17]提出基于关键装配特性的大型零部件最佳装配位姿多目标优化算法，实现了大型零部件最优位姿装配;杜福洲等[21]给出了飞机大部件对接过程测量能力指数的概念，构建了位姿测量不确定度与对接质量评估指标间的映射关系，实现基于位姿测量不确定度的飞机对接质量评估。本文拟通过使用多个激光位移传感器测量两部件关键特征之间的距离，建立结合理论测距距离或前期对接实际距离的位姿估计模型，从而得到部件间的位姿关系并解算驱动量。采用蒙特卡洛仿真方法研究安装误差对调姿量的影响，结合模拟件验证算法及系统的有效性。

1 基于激光测距的对接系统

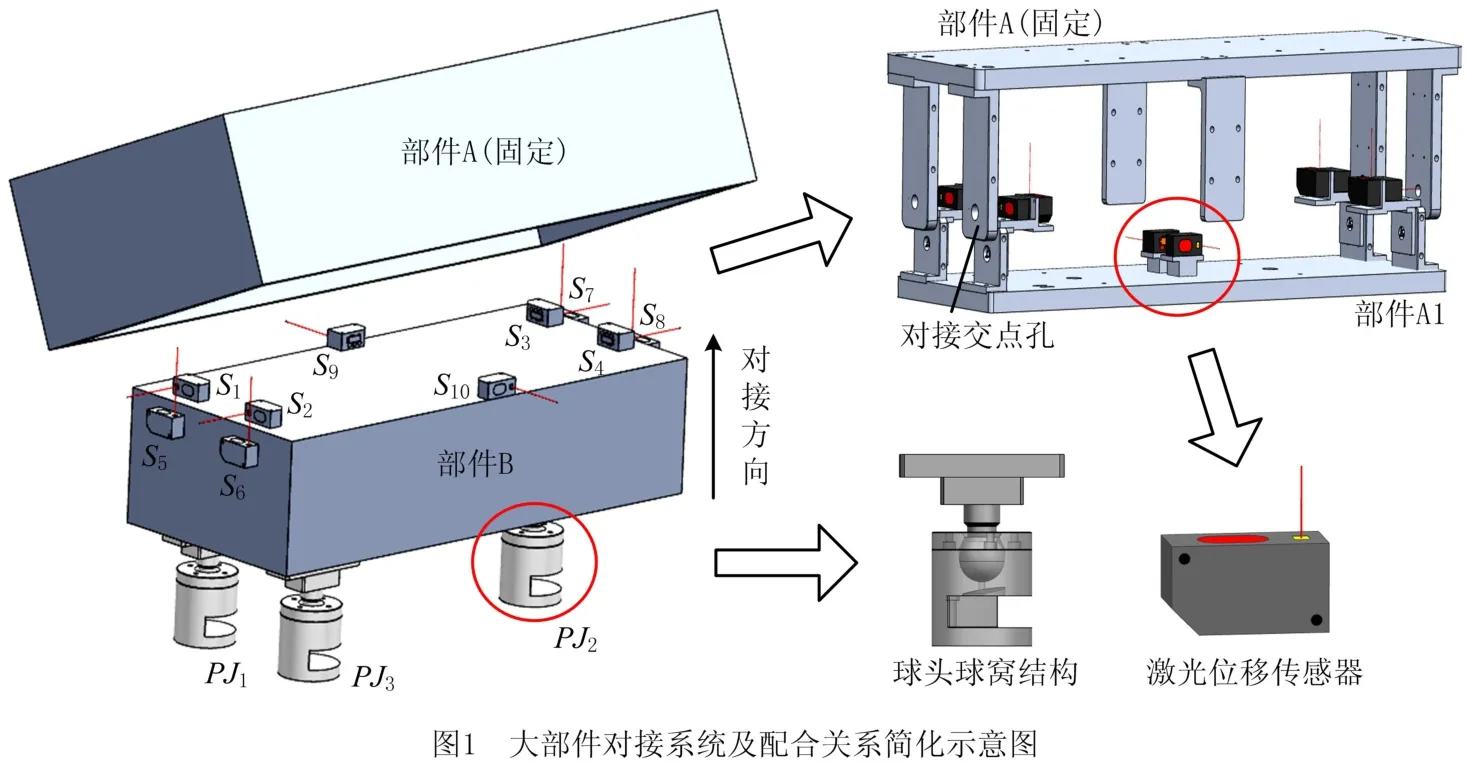
图1所示为一种典型的大部件对接方式，左侧结构为系统的配合关系简化示意图，部件A 和A1通过左右两侧凸耳中的交点孔实现对接。在对接过程中，A使用高强度的托架固定支撑。A1与托架、调姿定位结构连接。位移传感器通过可拆卸适配结构安装于A1，用于测量与A 的相对位姿，其中传感器S1～S4用于左右测距，传感器S5～S8用于上下测距，传感器S9和S10用于前后测距。数控定位器球头部件与A1固联，球窝与数控定位器连接。对接控制台可实时接收测量系统数据，调整对接过程中的位置姿态。

部件采用如图2所示的流程对接。首先，将A运至对接站位，将A1和定定调姿平台运至A下方。然后，对接控制软件以理论数模或前期对接得到的测距值为依据，与激光位移传感器的当前测距值进行比较，采用基于激光测距的对接方法解算出定位器各轴调整量并进行调姿，迭代此调姿测量过程直至满足调姿量小于设定阈值，从而复现理论数模中的对接状态或前期对接状态;A与A1对准后，在对接交点孔处插入连接螺栓，最后将调姿平台及托架等运送至停放区，完成对接。

2 基于激光测距的对接原理

2.1 定义坐标系

目前，大部件对接方法主要是利用关键特征点的测量值与理论值之间的匹配关系[22-26]，本文采用激光测距方法完成对接，根据多个位移传感器当前测距值与理论测距值之间的关系，计算运动部件A1复位所需的沿坐标轴平移旋转的运动量，然后将该运动量转换为数控定位器轴的调姿量来驱动部件运动，完成调姿。

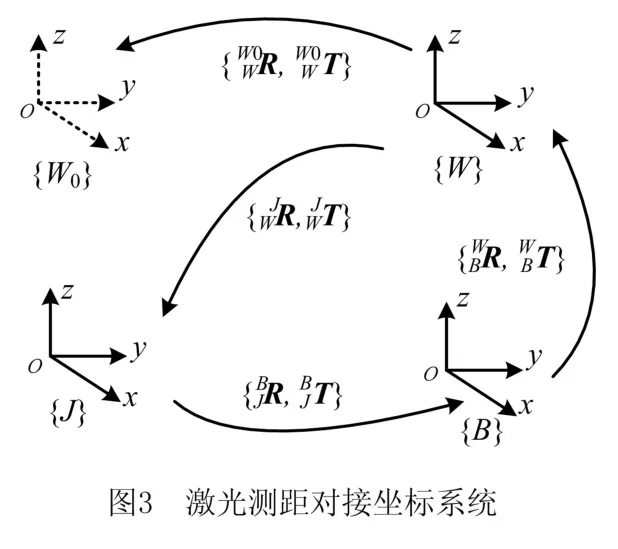
为实现上述调姿过程，首先需要利用运动学分析和姿态评估方法，构建如图3所示的坐标系，包括三轴定位器坐标{Ji}、平台坐标系{B}、部件A1当前坐标系{W}和部件A1目标坐标系{W0}。对接算法主要分为:部件A1当前坐标系与平台坐标系变换关系的构建、部件A1目标坐标系与当前坐标系变换关系的构建和数控定位器驱动量计算3部分。

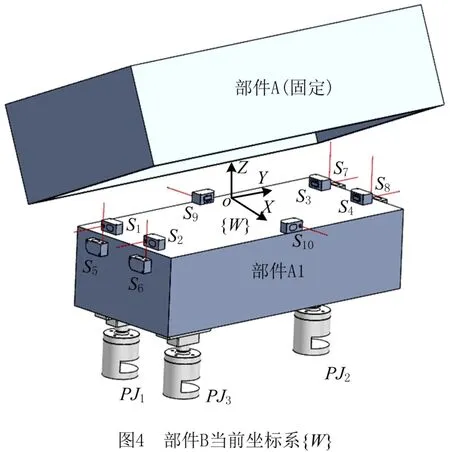
2.2 部件A1当前坐标系与平台坐标系变换关系

如图4所示，部件A1当前坐标系{W}的原点设在接头组中心，Z向垂直于平板面，X、Y为平板相互垂直的两个中轴线，平台坐标系{B}设在底座上，第i个定位器球心为PJi(i=1，2，3)，其在{W}下的坐标{WPJi}，由定位器系统反馈得到定位器球心在平台坐标系的坐标{BPJi}，计算获得部件A1 当前坐标系与平台坐标系变换关系

{W}与{B}可以通过旋转矩阵R和平移矩阵T进行转换，设当前坐标系{W}在平台坐标系{B}下的为姿态为(ωx，ωy，ωz，tx，ty，tz)T，其中，tx，ty，tz表示{W}原点在{B}的位置;ωx，ωy，ωz表示{W}相对于{B}的欧拉角，因此得到{W}和{B}的转换关系:

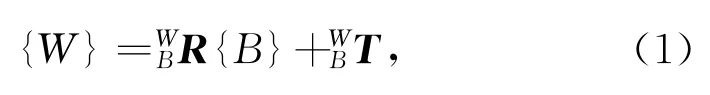
其中:

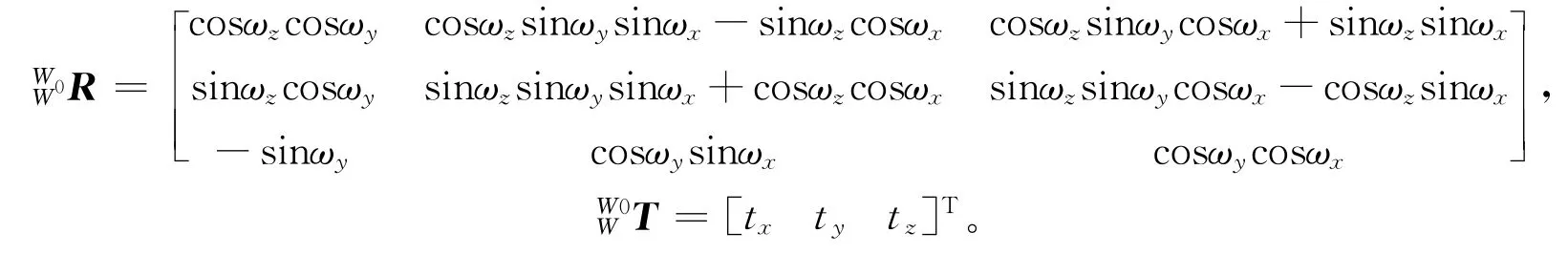
位姿参数可以通过奇异值分解(Singular Value Decomposition，SVD)进行求解[20]。SVD的实质是计算点集的质心在2个坐标系中的坐标，假设它们也存在式(1)的坐标转换关系，再实现所有的点在2个坐标系中的最小偏差拟合，具体步骤如下:

(1)分别计算球心的质心在{W}和{B}的坐标WP0和BP0:

(2)计算协方差矩阵H:

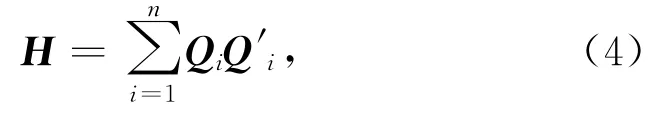
其中Qi=WPJi-WP0，Q'i=BPJi-BP0;

(3)对H进行奇异值分解:

其中D是对角矩阵，V和U是正交矩阵;

通过式(2)～式(7)，可以得到部件A1当前坐标系与平台坐标系变换矩阵

2.3 部件A1目标坐标系与当前坐标系变换关系

设当前坐标系{W}在目标坐标系{W0}下的描述为(ωx，ωy，ωz，tx，ty，tz)T，其中:tx，ty，tz表示{W}原点在{W0}的位置;ωx，ωy，ωz表示{W}相对于{W0}的欧拉角，因此得到{W}和{W0}的转换关系:

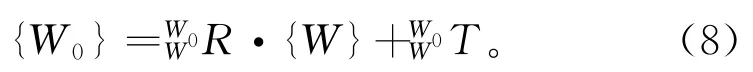
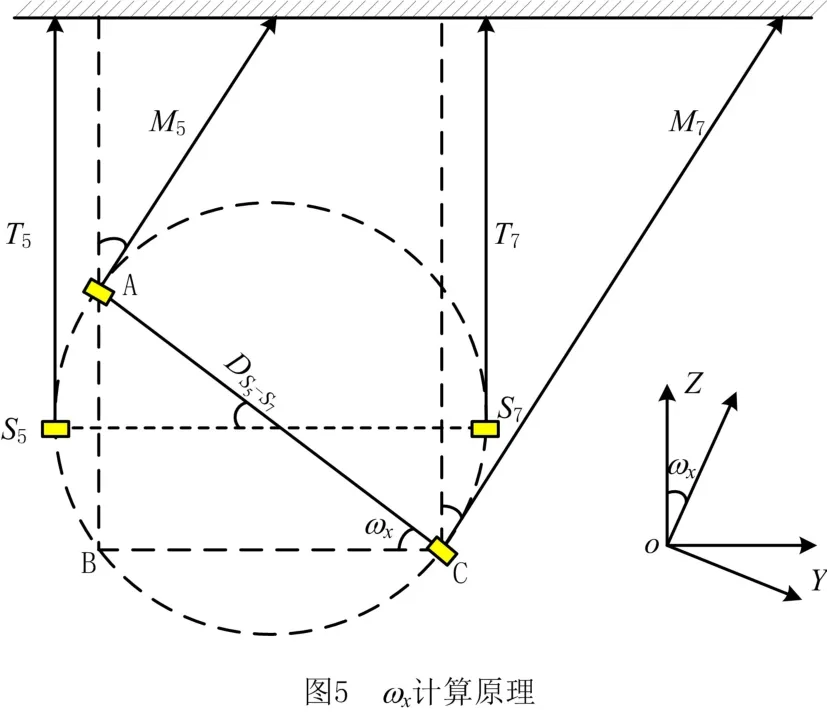
以ωx为例，计算原理如图5所示。图中:实线为当前位姿，粗虚线为目标位姿，剖面线表示机身;T5和T7表示处于目标位置时传感器S5和S7的测距值，M5和M7表示处于当前位置的传感器S5和S7的测距值，表示传感器S5和S7之间的距离;图中所标角度均为ωx;细虚线为计算辅助线。分析直角三角形ABC可得到如下公式:

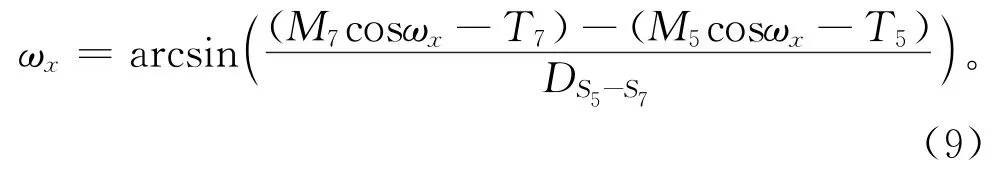
由于旋转角度较小，简化式(9):

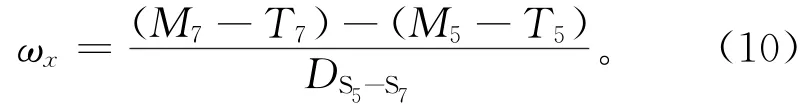
如图4所示，传感器S5，S7和S6，S8的分布相同，因此得到

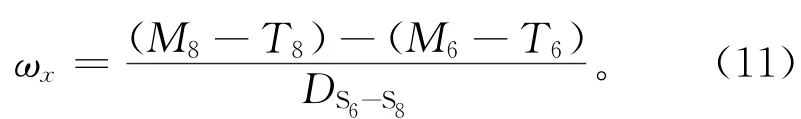
ωx的最终计算公式为:

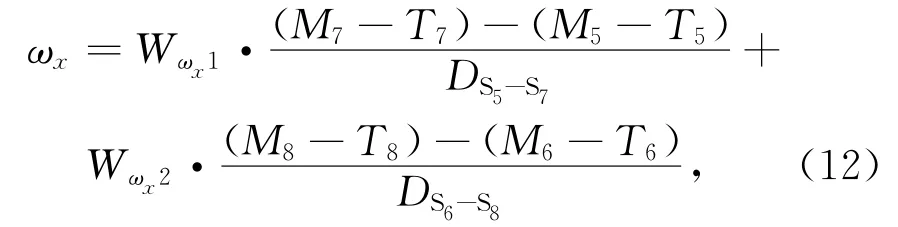
其他变量的计算方法类似，最终得到(ωx，ωy，ωz，tx，ty，tz)，

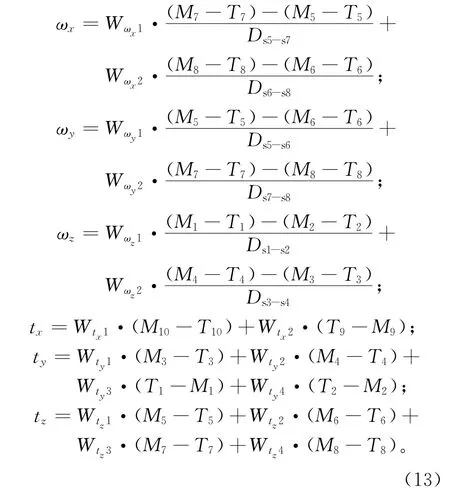
由于旋转角度很小，旋转矩阵可以简化为

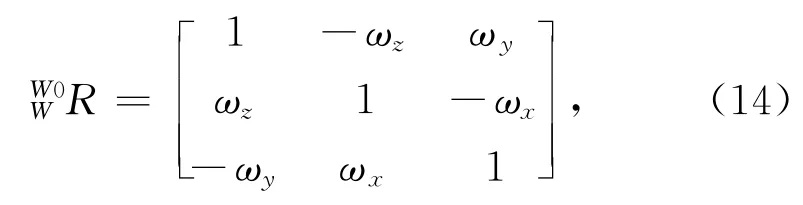
通过式(8)～式(14)，可以得到部件A1目标坐标系与当前坐标系变换矩阵

2.4 数控定位器驱动量计算

由于球头部件与部件A1 固联，因此球心在部件A1坐标系下的坐标始终不变，即W0PJi=WPJi，具体坐标系可以从理论数模中得到。设定位器球心新的位置在平台坐标系下的坐标为{BPJ'i}，则有如下关系式:

定位器系统反馈得到当前球心在平台坐标系的坐标{BPJi}，通过式(17)计算得到三个定位器最终的运动量λi，式中为第i个定位器坐标系向平台坐标系的转换矩阵。

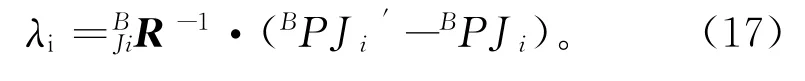
2.5 典型应用场景

飞机装配中，机身机翼常使用叉耳式连接或孔-销-孔形式连接，其基本原理类似[27]。以孔-销-孔连接为例，其接头布局形式又通常分为平行布局和垂直布局，飞机翼身对接两种接头布局形式如图6所示。设T1表示目标位置时传感器S1的测距值(理论数模或前期对接得到的测距值)，M1表示处于当前位置时传感器S1的测距值，表示传感器S1和S3之间的距离，表示传感器S5到S2和S4连线的距离(即y向距离)，其他变量命名方法相同，w表示权重。

如图6a所示，在机翼上布置6个位移传感器，其中:S6测量翼身x向的相对位置，S1和S3测量翼身y向的相对位置，S2，S4，S5测量翼身z向的相对位置。采用2.3节的计算方法可以得到机翼复位所需要的运动量:

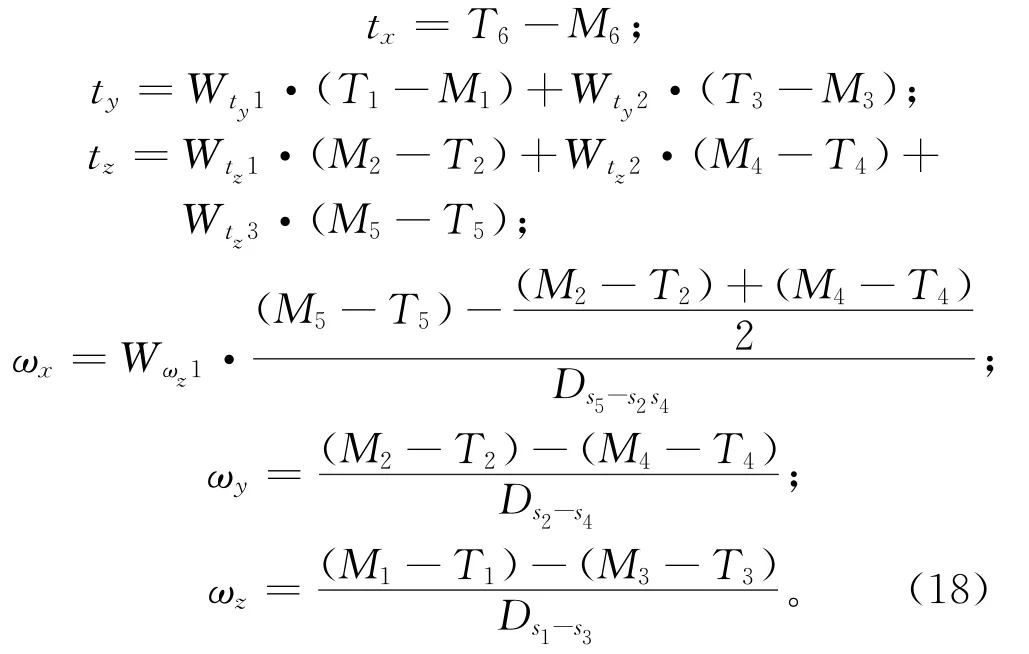
如图6b所示，在机翼和机身上共排布6个位移传感器，其中:S1和S3安装在机身上，用于测量y向相对位置;S2，S4，S5安装在机翼上，用于测量z向相对位置;S6安装在机身上，用于测量x向相对位置。同样使用2.3节方法可以计算如下运动量:

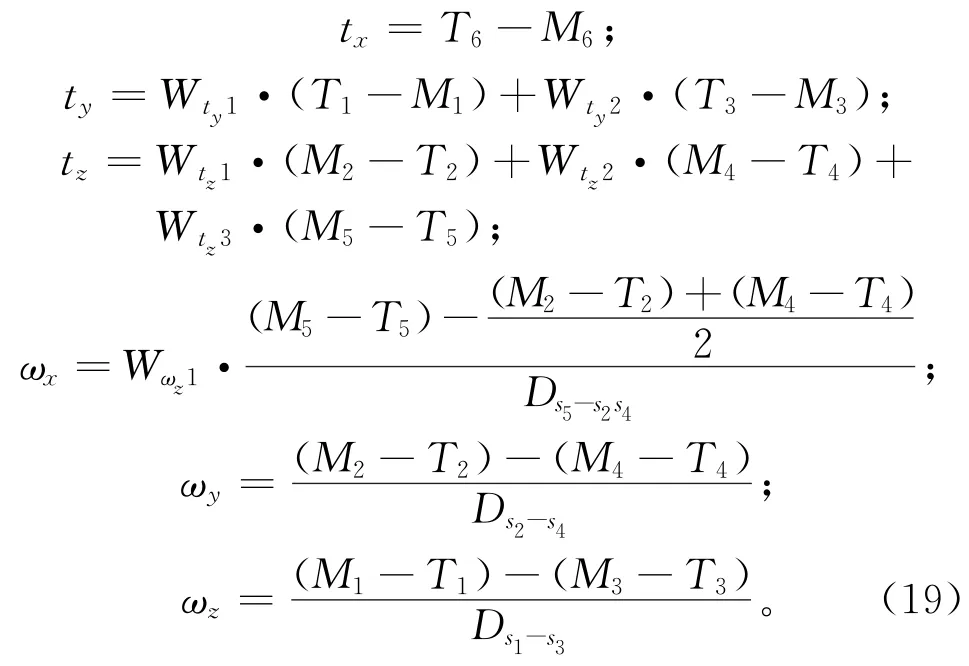
由式(18)和式(19)看出，翼身对接接头使用水平或垂直布局形式，安装6个位移传感器即可约束xyz方向的平移旋转。得到机翼复位所需的运动量后，根据机翼与定位器运动轴的坐标转换关系，可以得到各轴的调姿量，将调姿量输入调姿系统，完成调姿。通过分析典型的飞机翼身对接场景，可以看出，基于激光测距的对接方法简单且对环境要求低，使用及维护成本小，数据处理方便，可应用于非开敞性结构。需要注意的是，在实际应用中，在同一方向可布置多个传感器，用于减小误差，提高对接精度。

3 对接实验系统与对接结果

3.1 实验系统结构

本文搭建如图7所示模拟系统来验证算法，该实验系统主要包括模拟组件、全向移动平台、数控定位器、激光位移传感器和控制软件。数控定位器1、2、3均有X、Y、Z三个方向的驱动轴。模拟组件设置四对接头结构:两对直径为14 mm的孔，两对直径为16 mm的孔，对接孔的深度分别为16 mm和12 mm，精加工后的对接孔可达到小于0.02 mm 的配合公差。位移传感器型号为松下HG-C1030和HG-C1100，测距范围分别为30±5 mm和100±30 mm。

3.2 基于激光测距的对接实验流程

针对基于激光测距的对接精度测试具体步骤如下:

(1)调整模拟件运动到近似装配状态，记录各传感器测量值。

(2)将部件A1进行平移、旋转，但应保证各位移传感器激光点仍在部件A 耳片或底板上，同时耳片不产生碰撞。

(3)利用基于激光测距的调姿算法自动计算复位位姿所需运动量，驱动部件A1运动该运动量数值，使各位移传感器测量值与初始位姿下的值相同。

(4)与初始测距值进行比较，以差值作为基于激光测距的对接精度的参考指标。

3.3 实验结果及分析

通过多次实验发现，基于激光测距的对接一般需要2～3次迭代调姿，单次调姿所需时间小于1s。表1所示为对接迭代过程中的调姿量，其中第3次的调姿量达到设定阈值0.05 mm，无需运动，调姿结束。表2所示为对接过程中位移传感器的测距值。

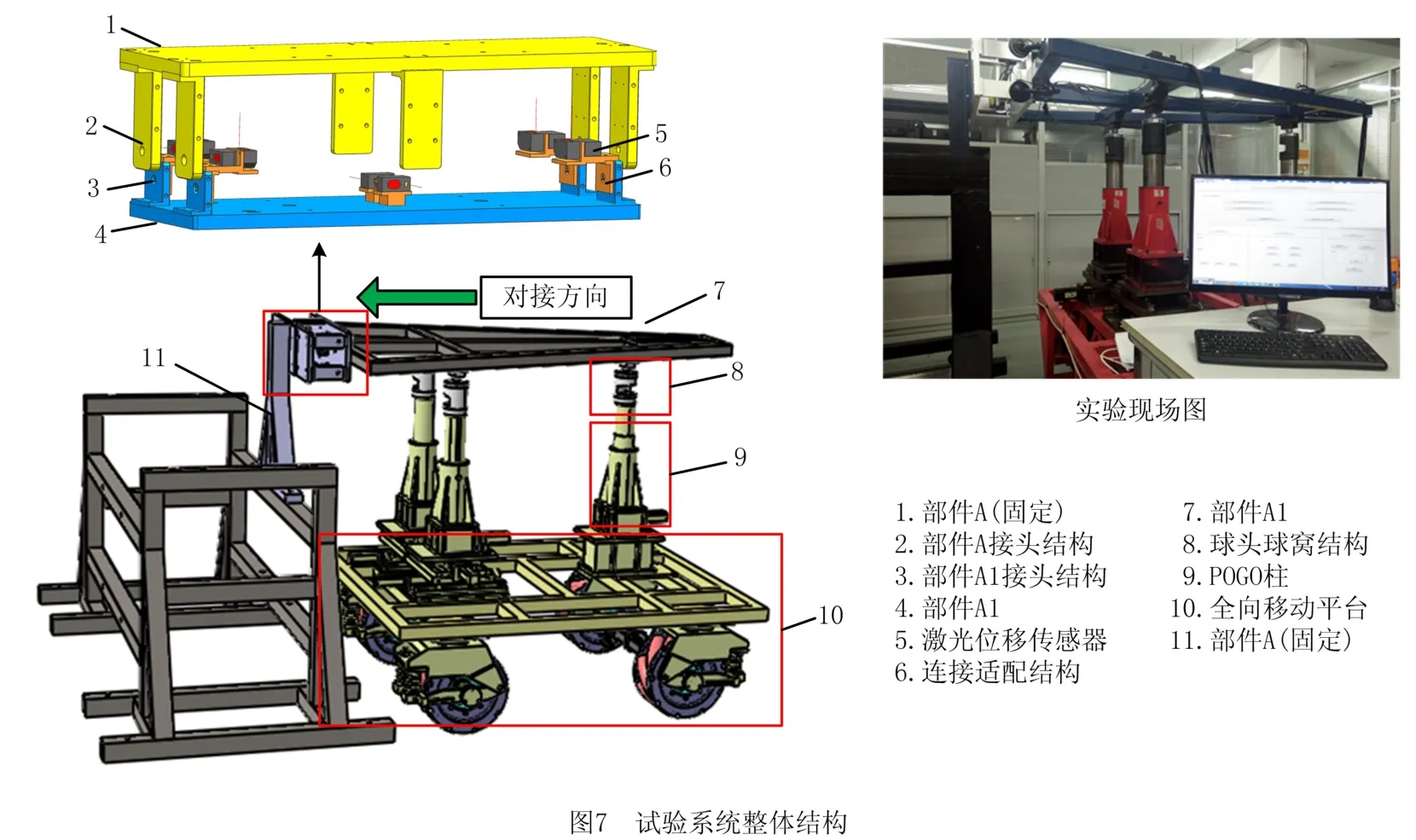
表1 对接过程中的调姿量

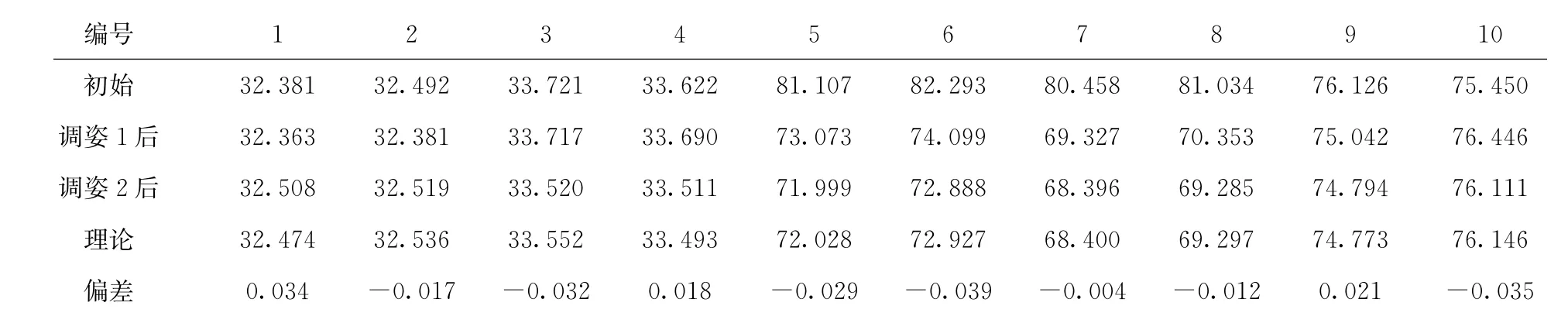
表2 对接过程中的测距值

由表1可见，第2次调姿量比第1次调姿量明显减小，迭代过程收敛;在表2中，第2次调姿后传感器测距值与理论值差值较第1次减小，表明实际位置更接近目标位置;两次迭代后，当前测距值与理论值差值小于0.05 mm，可以满足对接的精度要求。

4 误差分析

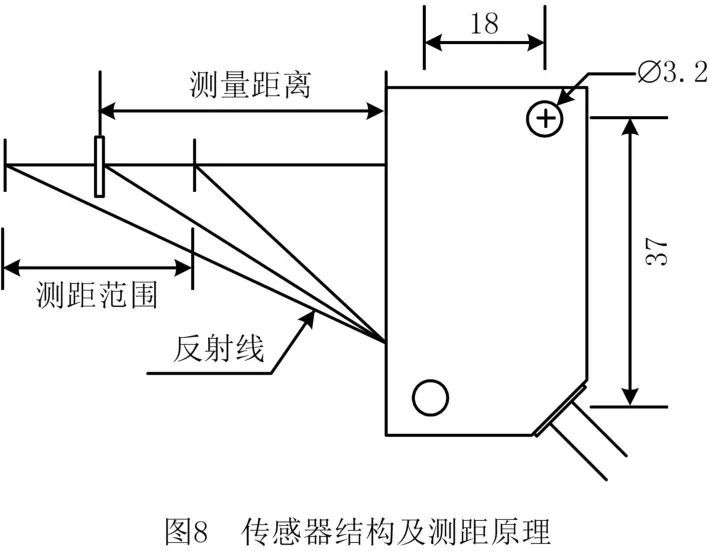
在基于激光测距的对接过程中，误差来源主要是仪器的数值波动误差及安装误差。位移传感器测距可达到的重复精度为10μm，对系统影响较小，不予以考虑。位移传感器结构及工作原理如图8所示，工程中使用φ3的螺栓连接通孔尺寸为φ3.2的位移传感器和机翼，孔轴线与螺栓轴线之间距离最大为0.1 mm。如图9所示，安装误差可分为传感器的平移和旋转误差，图中m表示测量值，s表示平移误差，α表示旋转误差。平移误差分析:沿测距方向的平移误差会影响传感器测距值;由式(9)～式(11)分析可知，垂直于测距方向的平移误差会影响传感器之间的距离。旋转误差分析:通过几何关系得到传感器可旋转的最大角度α=0.279°，对测距值影响极小。因此，本文主要考虑沿传感器测距方向和垂直测距方向的安装误差。

4.1 蒙特卡洛仿真思路

为了分析安装误差对调姿量的影响，本节拟采用蒙特卡洛方法进行仿真。假定位移传感器安装误差在两个方向(沿测距方向及垂直测距方向)均服从(-0.1，0.1)的正态分布且相互独立。选取6组初始位置及理论对接位置进行仿真计算，每种情况随机产生1 000组初始测距值，该值与实测值之间的差值服从(-0.1，0.1)的正态分布;同时产生1 000组传感器间距，该间距与理论距离之间的差值服从(-0.1，0.1)的正态分布，仿真分析已知误差存在的情况下初始测距值对调姿驱动量的影响。蒙特卡洛仿真流程如图10所示。

4.2 仿真结果及分析

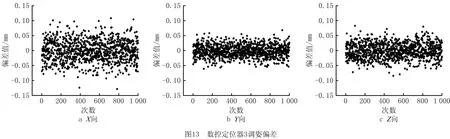
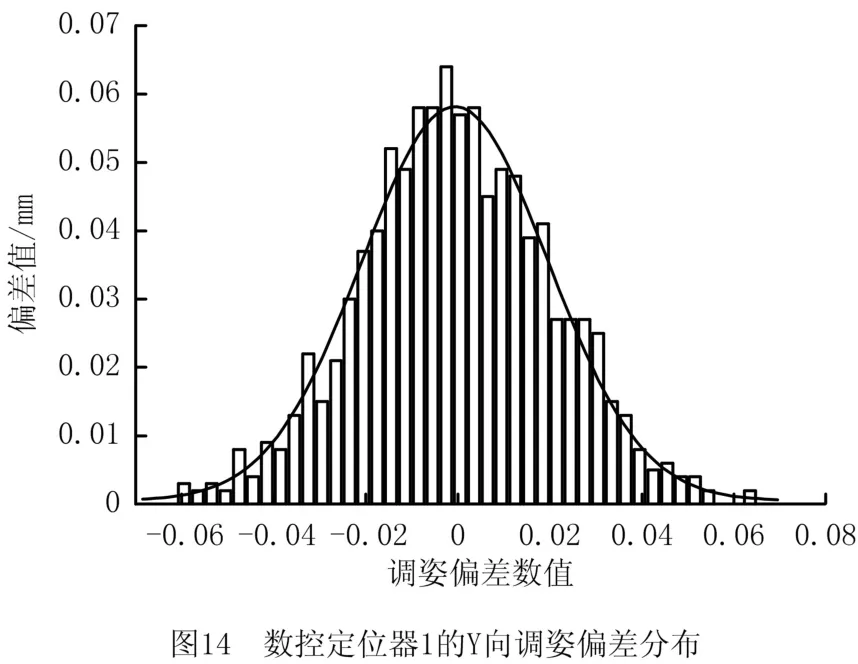
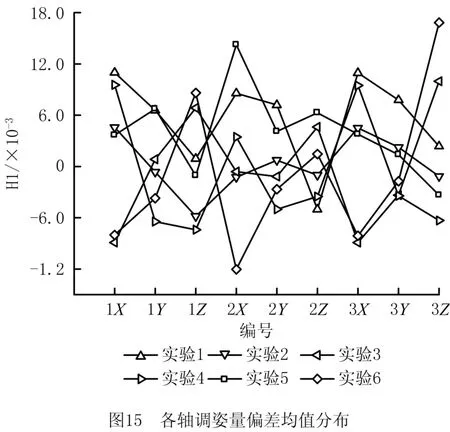
数控定位器1、2、3均有X、Y、Z三个方向的驱动轴，从6组仿真实验中选取其中某一组绘制如图11～图13所示的定位器调姿偏差分布，横坐标为仿真次数，纵坐标为驱动轴调姿量偏差。利用图11中数控定位器1的Y向调姿偏差数据绘制其频率分布直方图及拟合的概率密度，如图14所示。利用6组仿真数据计算各坐标轴调姿偏差的均值和标准差，绘制如图15和图16所示的分布图，横坐标为调姿方向(“1X”表示轴1的X方向)，纵坐标为6组姿态下的均值和标准差。

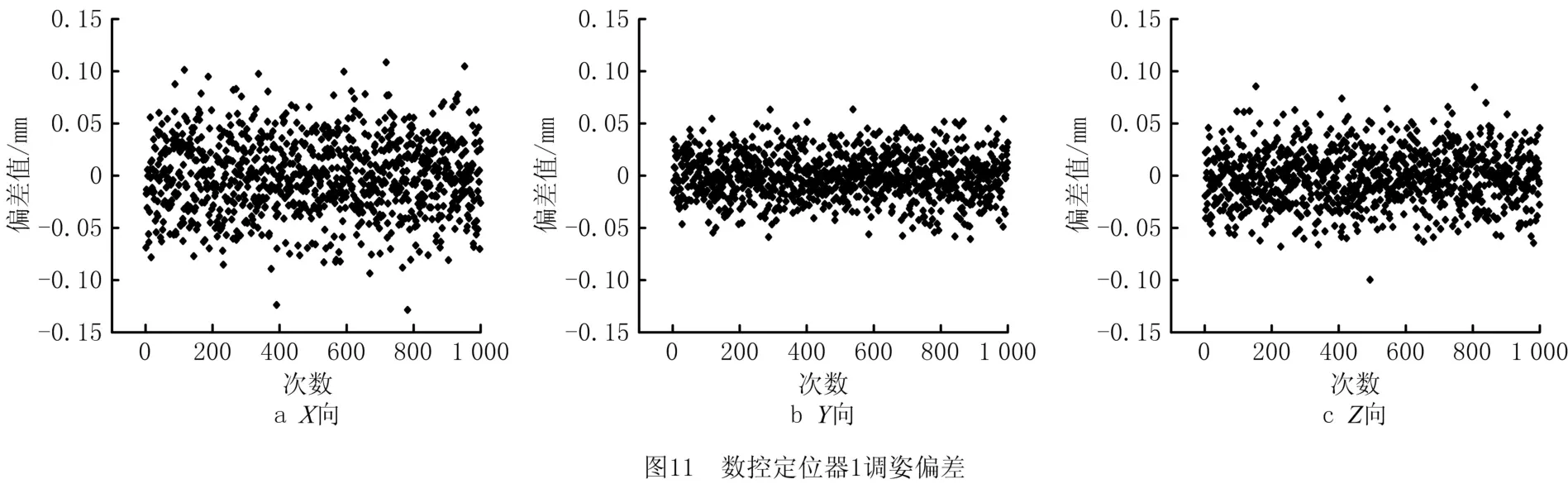
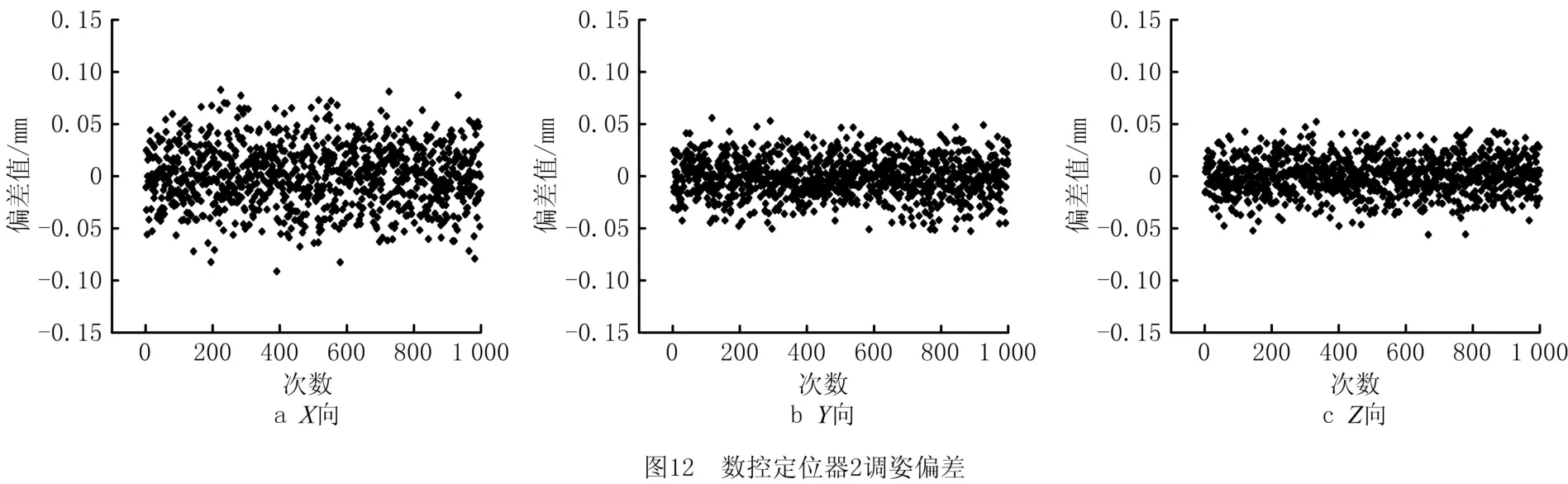
从图11～图13可以看出，X向调姿偏差波动范围较Y、Z向宽，与图16的调姿量偏差标准差分布情况一致，定位器2的3个方向偏差较定位器1和3小。结合如图4的结构(X向安装2个位移传感器，Y、Z方向分别安装4个位移传感器，定位器2附近的位移传感器数量多于定位器1和3)分析可知，位移传感器数目的增加有利于减小由安装误差导致的调姿偏差。

图15中，定位器各坐标轴偏差均值接近于零，结合图14分析，数控定位器1的Y 向调姿偏差呈对称分布，表明在传感器安装误差呈对称分布的情况下，调姿偏差近似对称分布。

图16中，6组仿真实验的定位器各坐标轴调姿偏差的标准差基本相同，说明部件不同的相对位置关系不会影响调姿偏差。除此之外，定位器1和3坐标轴调姿偏差标准差基本相等，结合定位器1和3的对称分布关系，分析得出当定位器呈对称分布时，调姿偏差分布规律基本相同。

5 结束语

本文针对大部件在复杂环境下的对接问题，研究了基于激光测距的对接方法，主要贡献如下:

(1)建立了基于SVD法的当前位姿模型、基于激光测距的目标位姿模型和调姿运动量解算模型。

(2)分析了安装误差对调姿量的影响，为后续研究提供理论依据。结论如下:在部件中安装多个激光位移传感器，可有效减小安装误差引起的调姿偏差;传感器安装误差呈对称分布时，调姿偏差近似对称分布;部件不同的相对位置关系不会影响调姿偏差;在定位器呈对称分布的情况下，调姿偏差分布规律基本相同。

(3)搭建模拟对接平台，实验验证了方法的有效性。实验结果表明:基于激光测距的对接一般需要2～3 次迭代过程，可实现的对接精度优于0.05 mm。