复杂非线性系统的子系统分解方法

2021-04-09谢苗苗张浪文谢巍

化工学报 2021年3期

谢苗苗，张浪文，2，谢巍，2

（1 华南理工大学自动化科学与工程学院，广东广州510641； 2 广东道氏技术股份有限公司，广东江门529400）

引言

信息技术和工业技术的发展推动着整体工业体系发生巨大的变化，诸多系统朝着越来越复杂的方向发展，如化工系统、灌溉系统、智能交通系统等，其典型特征为结构复杂、维数高、约束多、模型不确定、非线性。同时，对于这类系统控制的要求越来越高，要求获得更好控制效果的同时满足经济效益指标，通常传统的PID 控制难以满足系统对于工艺水平的要求，为满足安全、可持续性，先进的控制系统对于这些过程来说是必要的[1]。

模型预测控制（model predictive control, MPC）凭借其在处理多变量、状态/输入约束、非线性等问题上的优势，成为系统先进控制方法的首选[2-3]。通常，由于结构的复杂性、容错性以及计算问题，集中式MPC 通常存在控制时效性差、灵活性差等问题，因而在复杂过程中难以适用[4-5]。对于大规模过程的整体控制，分散式MPC 是解决方案之一[6]。为了实现分散式MPC，首先将一个大规模的过程分解成多个子系统，然后对每个子系统独立地设计控制，以达到减少控制器设计的复杂度[7-8]。分散式MPC的一个关键特性是子系统的控制器之间没有或很少有信息交换，由于通常化工过程单元之间的耦合是不可忽略的，使得分散控制下的全局性能受到限制[9]。在此背景下，分布式MPC 被提出，在协作分布式MPC 中，子系统通常使用全局代价函数[10]，在每个采样时刻，一个子系统MPC 都需要与其他所有子系统MPCs 通信，子系统MPCs 以迭代的方式计算它们的控制动作[11]，从而提高分布式MPC 的性能，诸多实际应用说明分布式控制框架能够提高计算效率、维护灵活性和容错性的发展的趋势。分布式控制系统的设计主要包括两个关键步骤[12]：(1)将整个过程适当地分解成更小的子系统；(2)提出一种经济有效的控制算法，在此基础上设计本地控制器并确定通信协议。

在过去的十五年里，分布式控制（特别是分布式MPC）算法的发展受到了极大的关注[13-14]。同时，同等重要的子系统分解得到的关注相对较少[15]。在文献中，有一些关于分布式控制系统分解算法的重要结果[16]。文献[17-18]针对过程网络的控制分解，采用了层次聚类的方法；文献[19]提出了一种面向系统分解的输入-输出配对方法，该方法能够同时考虑耦合结构和强度；文献[20]则基于社区发现算法，提出了一种非线性模型预测控制的分布式优化问题分解方法；文献[21]提出了一种相对时间平均增益序列的网络分解方法；文献[22-23]提出了面向分布式滚动时域估计的子系统分解方法，并在污水处理系统中进行了应用；文献[24]则将现有的社区发现算法推广到分布式状态估计和控制的共同框架内进行考虑。然而，上述基于社区发现算法的子系统划分均只考虑了系统的关联度，而忽略了不同变量之间的连接强度。先前的工作[25-26]提出了一种基于加权边的群组检测的子系统划分方法，并研究了其在分布式状态估计中的应用，而对于面向分布式控制的加权社区发现算法尚未得到解决。

因此，本文同时考虑状态、输入和输出之间的关联性，研究面向化工过程分布式状态估计和控制的子系统分解方法。具体地，首先基于化工过程形成有向网络，在构建的网络中，状态变量、输入变量和测量输出变量都被视为节点，提出基于社区结构发现算法的子系统分解方法，并在化工过程实例的分解中进行验证，设计分布式MPC 算法实现来说明方法优势。

1 预备工作

1.1 问题描述

针对复杂非线性系统的子系统问题，通常考虑如下动态模型：

其中，x ∈Rnx、u ∈Rnu、y ∈Rny分别表示状态、输入和输出向量，f 表示系统的状态方程，h 表示非线系统的输出方程。为实现分布式控制，需要将系统(1)划分成如下描述的子系统模型：

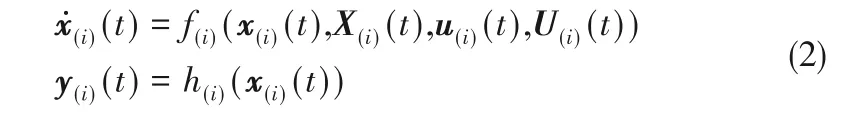
其中，i=1,…,p，p 为子系统的个数，x(i)∈Rnx(i)表示第i 个子系统的状态向量，u(i)∈Rnu(i)表示第i 个子系统的输入向量，y(i)∈Rny(i)表示第i 个子系统的测量输出，X(i)表示所有与子系统直接关联的子系统状态，U(i)表示所有与子系统直接关联的子系统对应的输入。

1.2 有向图

本文将构建加权有向图对系统(1)进行描述，有向图的构建方法可参考文献[24]，将系统的所有状态、输入和测量输出变量当作有向图的节点，这些节点通过有向边进行连接。令hj,j = 1,…,ny表示向量方程h 的第j 行；fi,i = 1,…,nx表示向量方程f 的第i 行；xi,i = 1,…,nx表示状态向量x 的第i 行；uk,k = 1,…,nu表示输出向量u 的第k 行；yj,j = 1,…,ny表示输出向量y的第j行。

根据如下规则定义有向图：

1.3 能观性与能控性

对于分解得到的子系统(2)，需要进行能观能控性检测。对于非线性系统，能观性的判断可以检验如下能观矩阵是否满秩：

类似地，对于得到的子系统(2)，能控性的判断可以检验如下能观矩阵是否满秩：

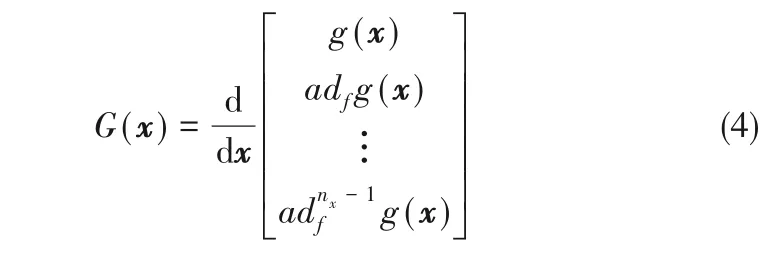
1.4 社区发现算法

社区发现算法用于将复杂网络划分成子网络，其构建方法可参考文献[27-28]，假设一个网络具有N个节点，其邻接矩阵A 的各个元素Aij可以通过如下方式构建：

同时，定义模块度进行分解结果的评价：

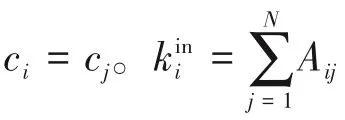
1.5 分布式Lyapunov MPC算法

在对系统进行子系统划分后，对其进行分布式模型预测控制来验证子系统划分的好坏，本文引入基于迭代子系统的分布式Lyapunov MPC[11]，即在时刻tk的实现如下步骤：

（1）控制器i接收和发送x(i)(tk)给它的下游邻居子系统。同时，它通过上游邻居的通信网络获得子系统状态x(l)(tk)；

（2）迭代控制器评估。

①在迭代c(c ≥1)中，控制器i 基于其上游邻居在迭代c-1 中评估的状态轨迹评估其未来的输入轨迹；

所采用的Lyapunov MPC i 的设计，在采样时间tk、迭代c中，被表述为以下优化问题：

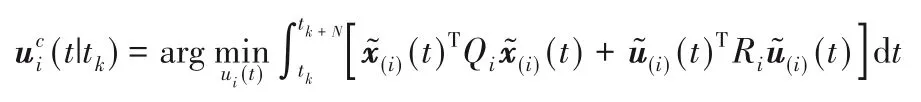
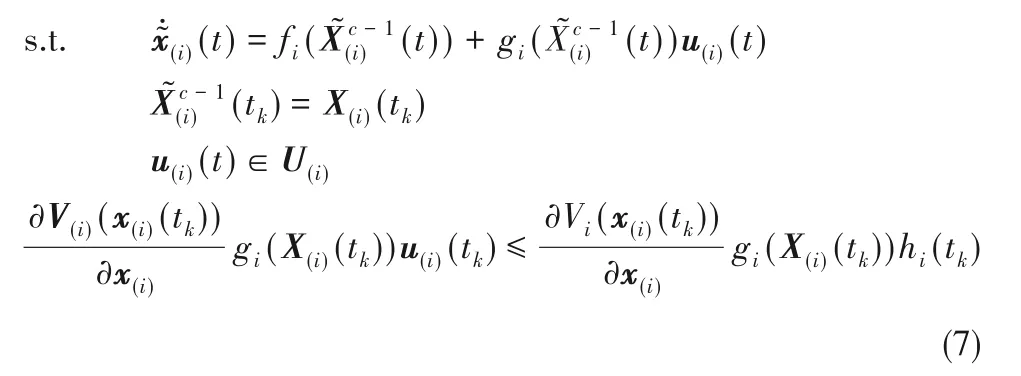
2 子系统分解方法

本文复杂非线性系统的子系统划分主要流程如图1 所示。首先，将非线性系统(1)用加权有向图进行描述；然后，构建系统的加权有向图，实施社区发现算法找到最大模块Q，得到推荐的子系统划分结果；最后，对所得到的子系统进行能观能控性判断。

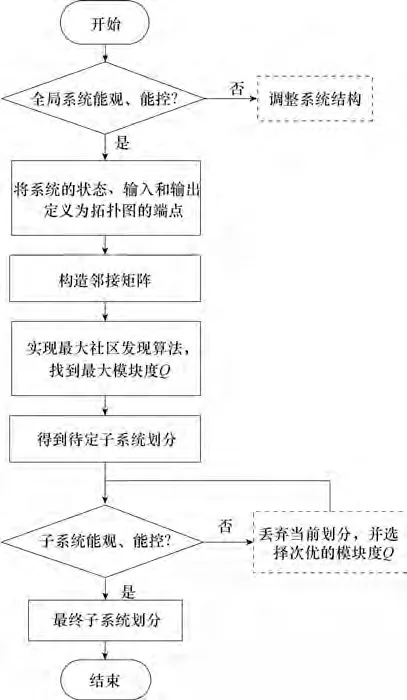
图1 复杂非线性系统的子系统的划分流程Fig.1 Flowchart of the proposed subsystem decomposition method of nonlinear systems.

2.1 加权连接边的定义

为考虑节点之间的连接强度，构建如下有向图连接边的敏感度，可以通过对非线性系统在工作点(xs,us)求一阶偏导得到：

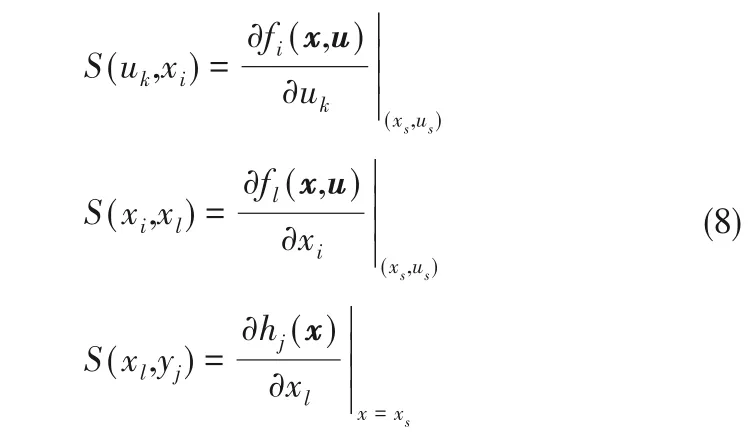
其中，S(uk,xi)表示从输入uk到状态xi的敏感度,S(xi,xl)表示从状态xi到另一个状态xl的敏感度，S(xl,yj)表示从状态xl到输出yj的敏感度。

进而，构建敏感度矩阵：

本节中，定义如下连接边的权重。

状态变量xi到另一个状态变量xl连接边的权重定义为(l,i = 1,…,nx)：

输入变量uk到状态变量xi连接边的权重定义为(k = 1,…,nu,i = 1,…,nx)：

状态变量xl到输出变量yj连接边的权重定义为：

当S(xi,xl)= 0，S(uk,xi)= 0 或S(xl,yj)= 0 时，连接边的权重为无穷，即两个节点之间没有直接连接。

2.2 最短路径

为构造加权邻接矩阵，需要找到两个节点之间的最短路径。假设P 为两个节点之间的路径，那么所有连接边表示为e ∈P，路径L(P)的长度为：

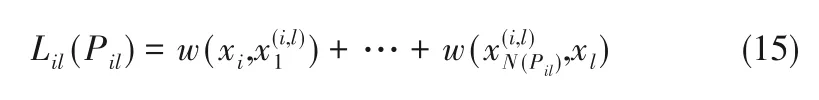
假设xi到xl的所有路径集合表示为，其最短路径为：

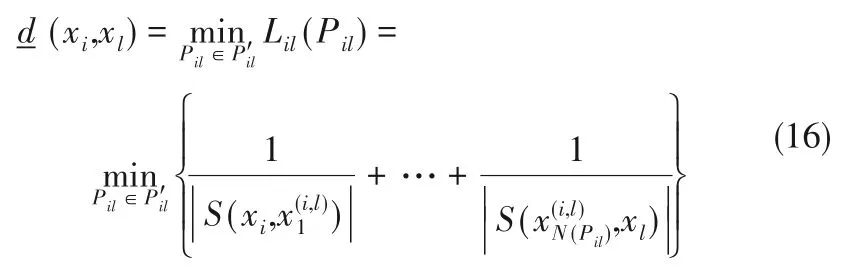
类似地，从输入变量uk到状态变量xi的路径长度Lki(Pki)为：

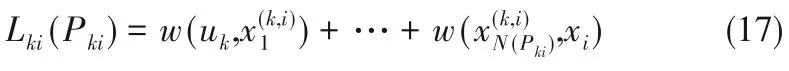
相应从输入变量uk到状态变量xi的最短路径(uk,xi)为：

其中，k = 1,…,nu,i = 1,…,nx，P′ki、Pki分别为从uk到xi的所有路径和其中一条路径。

从状态变量xl到输出变量yj的路径长度Llj(Plj)为：

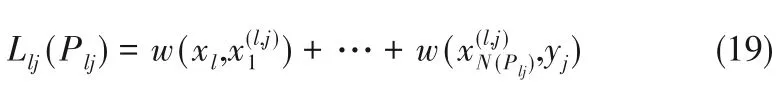
相应从状态变量xl到输出变量yj的最短路径(xl,yj)为：

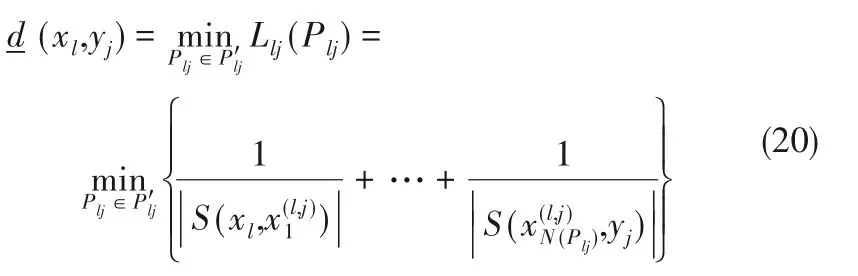
其中，l = 1,…,nx,j = 1,…,ny，、Plj表示从状态变量xl到输出变量yj的所有路径和其中一条路径。

从输入变量uk到输出变量yj的路径长度Lkj(Pkj)为：

相应从输入变量uk到输出变量yj的最短路径(uk,yj)为：

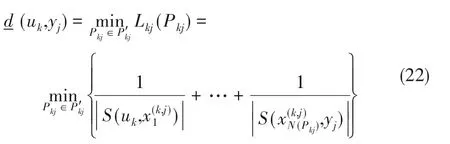
其中，k = 1,…,nu,j = 1,…,ny，P′kj、Pkj表示从输入变量uk到输出变量yj的所有路径和其中一条路径。

从输出变量yj到另一个输出变量ym的路径长度Ljm(Pjm)为：

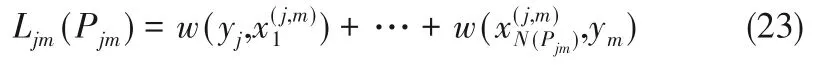
相应从输出变量yj到另一个输出变量ym的最短路径(yj,ym)为：

其中，j,m = 1,…,ny，P′jm、Pjm表示从输出变量yj到另一个输出变量ym的所有路径和其中一条路径，节点到自身的最短路径为(yj,yj)= ∞。

2.3 构建邻接矩阵

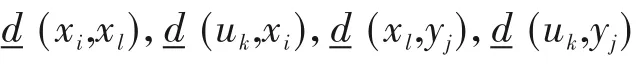
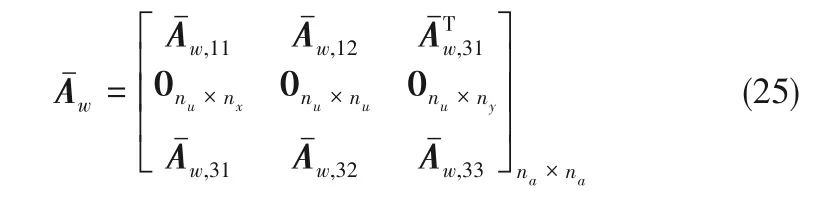
那么，所构建的加权邻接矩阵Aw将被用于社区发现算法，以对系统(1)进行划分。

那么，可以通过如下步骤构建加权邻接矩阵Aw。

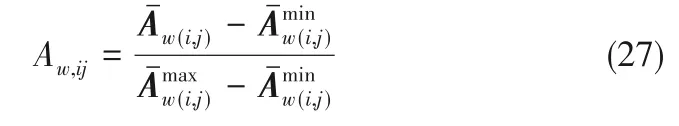
2.4 寻找最大模块度

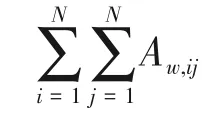
（1）对每个顶点i重复以下步骤：

①对于节点i 的每个邻居节点j，通过将节点i从当前群组移动到节点j 所在的群组，计算模块度的变化值ΔQw；

②找到上一步中最大的ΔQw＞0，将顶点i放入到相应的群组中，得到新的分组。

（2）令nc(k + 1)作为节点集结后的群组数量，如果nc(k + 1) ＜nc(k)，回到步骤（1）。否则，找到最大化的模块度Q。

那么，最大化模块度Q 对应的分组即为本文的子系统分解结果，然后，对所得到的子系统进行能观能控性判断，如果满足，则当前分解为最优分解，如果不满足，则找到第二大的模块度Q 对应的分解方案，以此类推。

图2 两个CSTR和一个分离釜的复杂反应分离器系统Fig.2 Two CSTRs and a flash tank with recycle stream

3 仿真验证

本研究考虑的过程是由两个连续搅拌反应釜(continuous stirred tank reactor, CSTR)和一个快速分离釜组成的三个容器的复杂反应分离器系统（图2）[30]。第一个CSTR 包含反应物A，转化为所需的产物B。物种A也可以反应成副产品C。溶剂不反应，标记为D。第一个CSTR 的出水和额外的新鲜饲料构成了第二个CSTR 的入口。反应A→B 和A→C（分别称为1 和2）在两个CSTR 中串联进行。假设三个容器都有静态滞留。

在标准建模假设下，通过材料和能量平衡获得的描述系统行为的动力学方程如下：

式(29)中各参数值见表1。每个储罐都有一个外部热量输入/排出。所需的工作点xs是过程的不稳定稳态点，为xs=[369.5,3.318,0.172,0.042,435.3,2.751,0.446,0.111,435.3,2.882,0.497,0.120]T。

闪蒸罐分离器模型的运行假设是：在闪蒸罐的工作温度范围内，每种物质的相对挥发度保持恒定。该假设允许根据容器液体部分的质量分数计算塔顶的质量分数。还假设分离器中发生的反应量可以忽略不计。对塔顶流的组成与闪蒸罐中持液率的组成进行建模：

式中，xD是闪蒸罐液含率中溶剂的质量分数。

对该化工过程实施本文提出的分解方法，并和文献[11,30]中的方法进行比较，得到了三个分解：文献[30]中根据物质种类划分方法的分解1；根据文献[11]的结构划分建议得到的分解2；应用本方法的分解3。这三个分解如表2 所示。实现本文子系统分解的计算时间0.068 s。

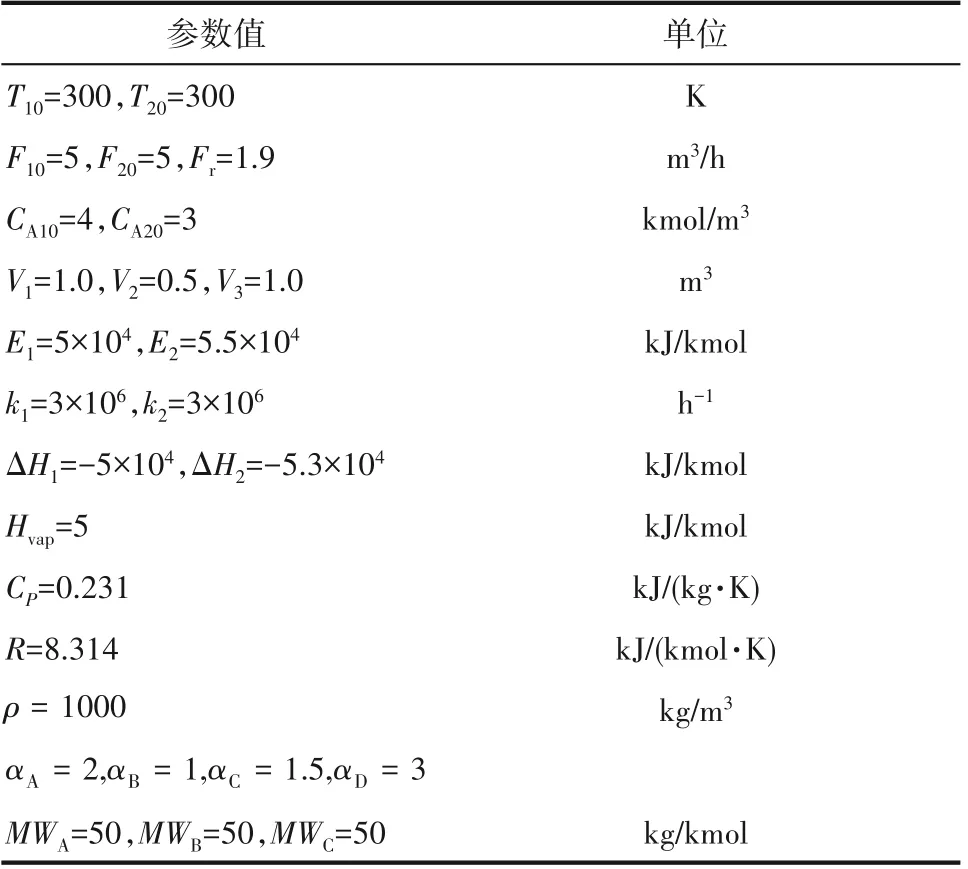
表1 式（29）、式（30）中的参数值Table 1 Parameter values in Eq.（29）and Eq.（30）

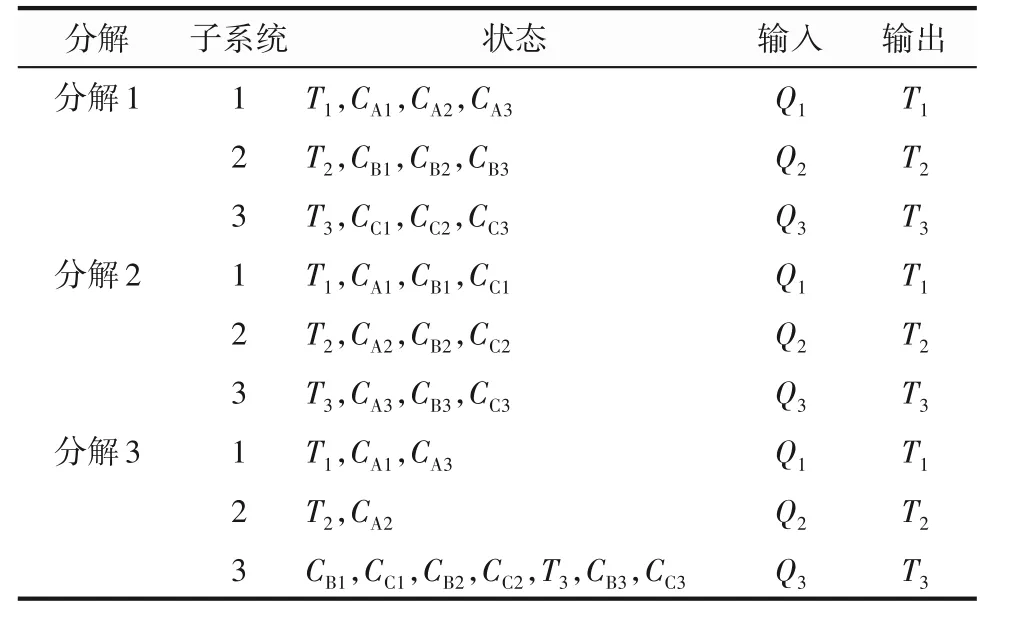
表2 系统（29）的三种分解Table 2 Three decompositions for system（29）

分别对表2 中的分解1、2、3 进行分布式Lyapunov MPC 控制实现。在不同的Lyapunov MPC实现下，每次运行将使用相同的初始条件和干扰序列。初始系统状态设定为：x0=[356.9, 3.227, 0.030,0.015, 446.5, 2.696, 0.465, 0.125, 446.5, 2.821,0.530,0.139]T。

定义性能指标如下：

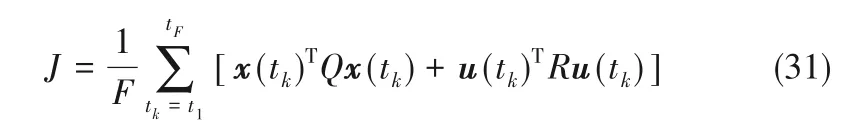
首先，比较了无干扰的情况，两个分解模型在一次评估中，分布式Lyapunov MPC 迭代次数为2 次实现时，标称闭环系统的温度和输入轨迹如图3 所示，性能指标和平均CPU 时间如表3 所示。图3 和表3 的结果表明，考虑耦合强度的分解3 在一定程度上优化了性能，且没有过多消耗时间，在同样的控制策略下，本文所提出的分解方法子系统内部耦合更为紧密，能够提升控制效果。

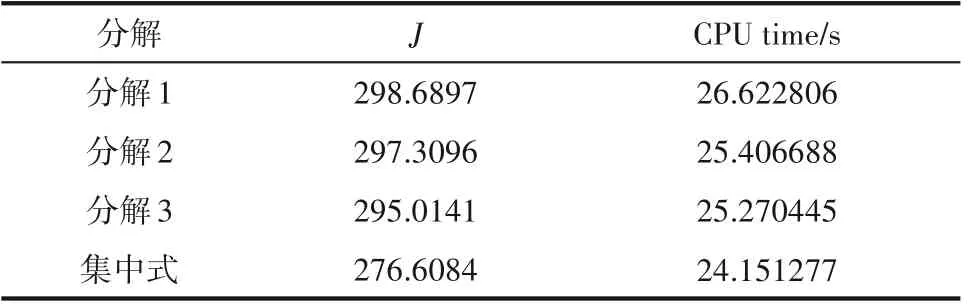
表3 不同分解模型的迭代分布式MPC和集中式MPC的性能指标（J）和CPU时间Table 3 Performance index（J）and CPU time of iterative distributed MPC with different decomposition models and centralized MPC

然后，为测试方法的抗干扰性，对三个子系统模型加入相同干扰。对每个子系统模型进行五次具有不同干扰序列的运行。性能指标和总CPU 时间如表4 所示，结果说明在相同的分布式控制器设计条件下，本文分解方法比分解1 和分解2 方法在性能上取得了更好的效果，说明考虑子系统之间的权重考虑，能够获得内部连接更强的子系统划分，提升分布式模型预测控制的性能。

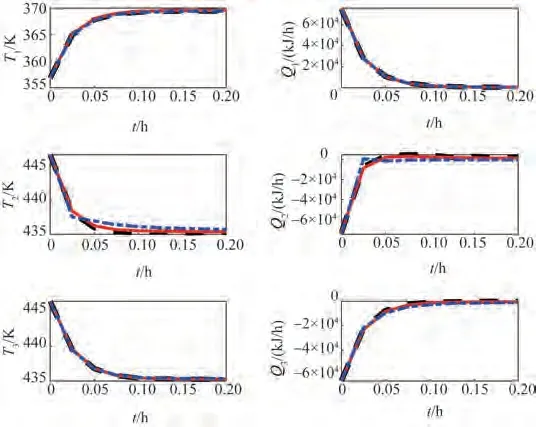
图3 分解1（蓝色点划线）、分解2（红色实线）和分解3（黑色虚线）的闭环系统的温度和输入轨迹Fig.3 Temperature and input trajectories of the nominal closed-loop system under Decomposition 1(blue dash dotted line),Decomposition 2(red solid line),and Decomposition 3(black dotted line)

最后，针对分解3 进行不同迭代次数的分布式Lyapunov MPC 实现的比较，其参数值与第一组仿真相同，分别考虑了迭代次数为1 次、2 次和3 次的情况。闭环系统的温度和输入轨迹如图4 所示，消耗的性能指标和平均CPU 时间如表5所示，结果表明，随迭代次数增加，虽然计算时间增长，但控制性能提升，在迭代2次时，性能收敛。

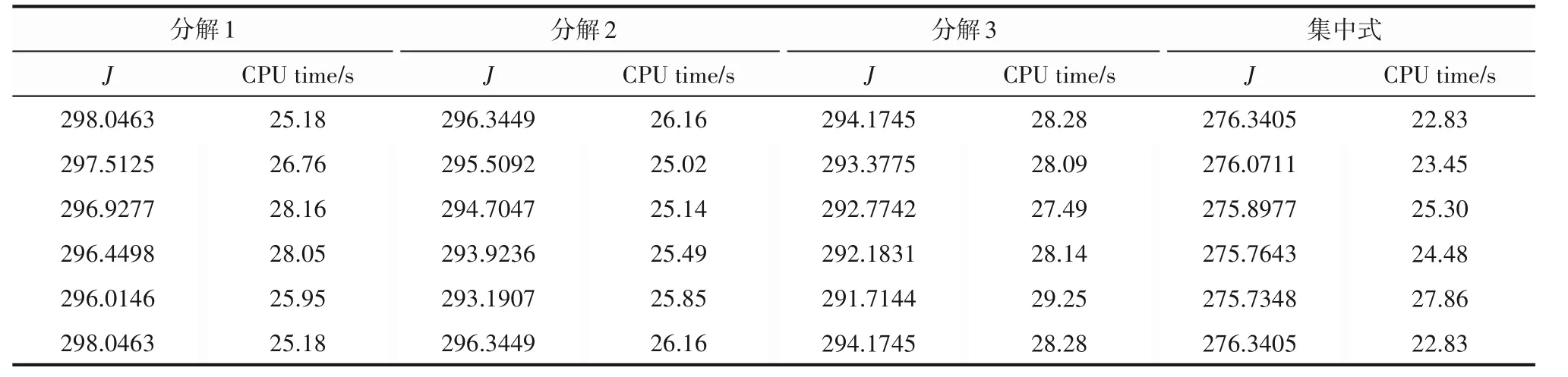
表4 不同分解模型的分布式MPC和集中式MPC在5次运行中的性能指标（J）和CPU时间Table 4 Performance index（J）and CPU time of distributed MPC with different decomposition models and centralized MPC in five runs

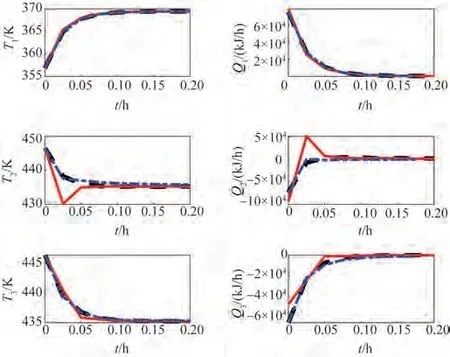
图4 分布式LMPC在迭代1次（红色实线），2次（黑色虚线），3次（蓝色点划线）时的温度和输入轨迹Fig.4 The temperature and input trajectories of distributed LMPC when iteration times is 1(red solid line),2(black dotted line)and 3(blue dash dotted line)

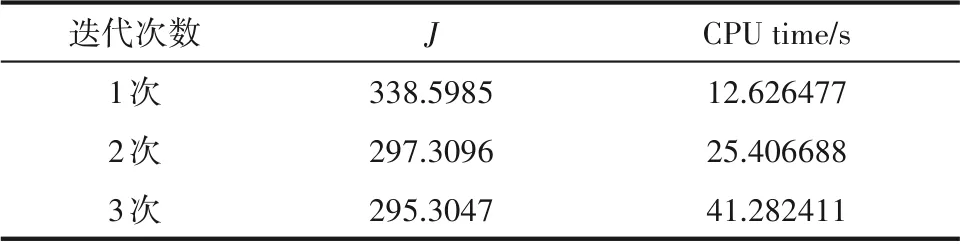
表5 不同迭代次数的分布式LMPC的性能指标和CPU时间Table 5 Performance index and CPU time of distributed LMPC with different iteration times

4 结论

提出了一种复杂化工过程的子系统分解，用于考虑耦合强度的分布式状态估计和控制，在连续搅拌反应釜过程的实例仿真表明，在不改变控制策略的前提下，本文提出的分解方法提升了过程控制性能。相对比只考虑系统连接度的子系统划分方法，本文分解方法得到的子系统内部之间连接度更强，而子系统之间的连接弱，因而更适合用于分布式控制设计。未来可以考虑改进连接边权重的定义，使之能够更好地反映系统的连接强度，应用于更为复杂的系统分解，并通过设计分布式状态估计进行综合验证。

符号说明

CA1,CA2,CA3——分别为A在容器1、2、3中的浓度，kmol/m3

CB1,CB2,CB3——分别为B在容器1、2、3中的浓度，kmol/m3

CC1,CC2,CC3——分别为C在容器1、2、3中的浓度，kmol/m3

CAr,CBr,CCr——分别为A、B、C在循环中的浓度，kmol/m3

CA10,CA20——分别为容器1、2进料流中A的浓度，kmol/m3

CP——比热容，kJ/（kg·K）

E1,E2——分别为反应1、2的活化能，kJ/kmol Fr——循环流量，m3/h

F1,F2,F3——分别为容器1、2、3的出水流量，m3/h

F10,F20——分别为进料流至容器1、2的流量，m3/h

Hvap——汽化热，kJ/kmol

ΔH1,ΔH2——分别为反应1、2的反应热，kJ/kmol