正反馈式流体振荡器内部流动特性的数值模拟

别海燕，黄晨，安维中，李玉龙，林子昕

（中国海洋大学化学化工学院，山东青岛266100）

引 言

振荡器是一种以流体为工作介质，能在入口提供定常流动，出口产生非定常流动的流体器件[1]。由于振荡器具有结构简单、无运动部件、体积小、操作方便、运行可靠、免维修等优点，特别适用于强辐射、强振动、强腐蚀等极端复杂的环境[1-5],被广泛应用于膨胀制冷[6-7]、航空航天[8-10]、环境治理[11-14]和石油化工[15-17]等领域。

通过喷嘴的一股射流，由于射流扩散和卷吸作用，其将偏转并逐渐沿着其中一个扩张壁面流动，形成柯恩达效应。振荡器中的射流振荡正是由柯恩达效应产生的，流体经入口流入喷嘴形成的主射流会发生偏转，并逐渐沿其中一扩张壁面流向同侧出口，同时在控制流的作用下，主射流发生偏转并流向另一个出口，如此周而复始引起射流的周期性振荡[18]。

振荡器的理论与数值方面，国内外学者进行了广泛的研究[19-24]。Bobusch 等[25]以水为工质进行了PIV 研究，发现捕获涡的几个区域是振荡过程的关键驱动因素。雷晗等[26]通过对不同结构的超音速附壁式振荡器进行数值计算和分析，揭示超声速流体振荡器的起振机制以及振荡器的部分结构参数对性能的影响规律。Pandey 等[27]对单出口射流振荡器进行了非定常RANS 模拟，研究了关键几何参数入口宽度、喉部宽度变化对振荡器内部流动结构和性能的影响。Wen 等[28]采用立体和二维粒子图像测速仪(PIV)测量方法，对扫描射流振荡器向开放空间发射的扫描射流产生的三维流动结构进行了实验研究，提出了一种基于适当正交分解的相平均流场计算方法。振荡器已被证明是一种有效的分离控制工具，但对其内部流动特性尚不完全了解。

本文采用三维数值模拟方法对具有正反馈通道的流体振荡器进行了模拟，利用三维雷诺平均模型（RANS）对其内部流场进行描述，阐明了正反馈流体振荡器的内部流动特性，定量地描述振荡器内部的压力变化和质量流率变化。

1 计算模型

1.1 物理模型

正反馈流体振荡器的主要结构包括振荡器入口、喷嘴、反馈回路、振荡腔、分流劈、射流出口[29]，其结构如图1 所示。根据杨军[30]设计的射流振荡器模型，建立喷嘴宽度W 为4 mm，位差S 为1.2 mm，劈距H 为34 mm 的正反馈式流体振荡器模型，其中喷嘴宽度W 是确定整个振荡器尺寸的参考值。操作条件确定后，射流能否附壁、切换及振荡的稳定性就决定于振荡器的几何尺寸。

1.2 网格建立及无关性检验

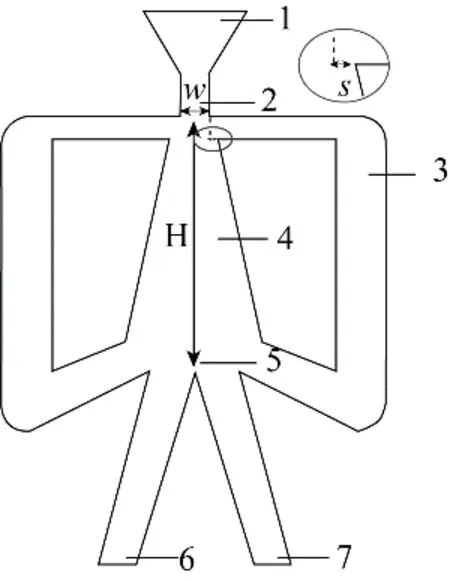
图1 正反馈式流体振荡器结构示意图Fig.1 Schematic diagram of feedback fluidic oscillator

图2 正反馈式流体振荡器的网格示意图Fig.2 Grid mesh of feedback fluidic oscillator

网格质量对计算精度、效率及模拟结果的可靠性具有一定影响。本模型采用边界层加密及分区的方式进行网格划分，在保证计算准确度的同时又提高了网格质量。其中流体振荡器由于反馈回路的反馈作用，主流从振荡器喷嘴射出后在腔体的两个支路来回切换，流动过程比较复杂，因此需对腔体和反馈回路区域进行网格加密；振荡器出、入口区域流体流动相对稳定，流体之间无激烈碰撞，在这一区域可使用较大的网格。图2为流体振荡喷射器的网格划分情况。

对同一流体振荡喷射器模型进行了三种不同尺度网格划分以检验网格无关性，划分后的网格数量分别为110674、445610 和2460245。通过比较不同网格尺度下各模型的振荡频率，发现模拟结果与网格数量基本无关。因此在保证计算精度的同时，为提高计算效率并节省计算周期，最终采用网格数量为445610的模型进行后续的模拟研究。

2 计算方法

2.1 湍流模型

由于流体振荡器中的射流流场具有流动方向的改变以及流线的弯曲等复杂特性，流动具有强烈的各向异性。在湍流模型的选择中。由于重整化群（RNG）k-ε 模型相比于最常用的标准（Standard）k-ε 模型，其在大部分流动问题的应用中都具有较高的精度，可以很好地模拟强旋流及流线弯曲的流动，能更好地运用于流体振荡器的流场中，所以本文模拟的湍流模型选择RNG k-ε 模型。

控制方程：

质量守恒方程（即连续性方程）

式中，ρ为流体密度，kg/m3；t为时间，s；ui为坐标三个方向的速度分量，m/s；xi为坐标轴三个方向的长度，m。

动量方程组：

式中，τij为亚格子紊动应力；μ 为流体黏度，Pa·s。

其湍动能k和湍流耗散率ε的方程如下：

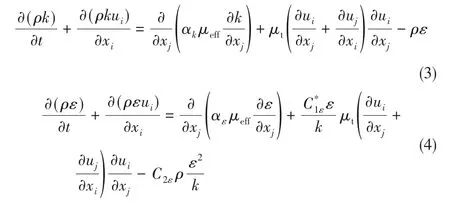
式中，

式 中，C1ε=1.42，C2ε=1.68，Cμ=0.0845，αk=αε=1.39，η0=4.377，β=0.012。

由于RNG k-ε 模型引入了时均应变率Eij，加入了旋流和旋转的影响，从而很好地改善了计算精度。

2.2 边界条件

振荡器的工作流体选用水作为流体介质，工作流体入口采用速度入口边界，设为1 m/s。振荡器的两个出口为压力出口边界，设为0.1 MPa。壁面均采用无滑移壁面边界条件。

2.3 求解设置

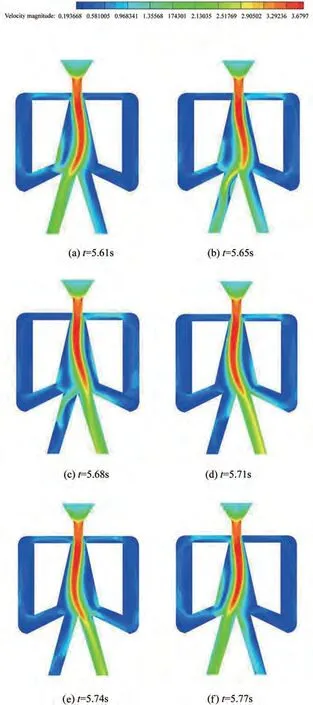
图3 一个周期内的正反馈式流体振荡器中间平面速度云图Fig.3 Mid-plane velocity contours of feedback fluidic oscillator in a cycle

求解设置采用有限体积法对瞬态控制方程进行离散，非耦合隐式方案进行求解。进行数值模拟时，对控制方程在空间上进行离散，在每个时间步上进行离散方程的求解。在时间域上采用二阶隐式格式。利用SIMPLE 算法求解实现压力与速度的耦合，速度修正方程中压力项采用Standard 方法，为保证收敛精度，动量方程、湍动能、湍流耗散率方程均采用二阶迎风格式。

3 结果与讨论

3.1 内部流动特性

图4 一个周期反馈流体振荡器的中间平面压力分布图Fig.4 Mid-plan pressure contours of feedback fluidic oscillator in a cycle

图3 为流体振荡器在z=4 中间平面上一个周期振荡的速度云图，该振荡模型的周期T=0.16 s，振荡频率f=6.08 Hz。在t=5.61 s 到t=5.65 s 阶段内，振荡腔内主射流偏向右侧壁面，同时有部分流体流入右侧反馈回路并在其中部聚集；在t=5.68 s 到t=5.71 s阶段内，主射流在喷嘴出口处受到反馈回路中流体的作用，使射流稳定附壁的力的平衡被打破，射流主流体向左侧偏移，并最终主射流附壁在左侧壁面，随着主射流的偏移，流体逐渐切换至右侧出口流出，同时有部分流体流入右侧反馈回路，完成了一次射流切换；在t=5.74 s到t=5.77 s阶段内，喷嘴出口处的主射流受左侧反馈回路流体的作用，逐渐向右侧壁面偏移，随着主射流的偏移，流体逐渐切换至左侧出口流出，形成了稳定的周期性振荡射流。

图4是正反馈振荡器中一个振荡周期内部压力变化过程。t=5.61 s 到t=5.65 s 阶段内，左侧壁出现作用范围较大的低压区，主射流向右偏移，右侧壁逐渐出现低压区，右侧壁处的低压区随时间不断增大下移，部分流体从右侧下游的反馈回路入口进入，并在其中部聚集，到一定程度时，右侧反馈回路中的总压上升，由于主射流的卷吸作用，将反馈管中的流体卷吸走，左侧反馈回路没有流体补足进而出现低压区；在t=5.68 s到t=5.71 s阶段内，左侧壁低压区域随时间逐渐变小，右侧壁低压区不断增长，增长到最大，主射流向左侧偏移，完成一次射流切换；t=5.74 s到t=5.77 s阶段内，右侧壁低压区渐渐消失，左侧壁低压涡流区逐渐增长达最大，左侧反馈回路中因部分流体流入总压上升，主射流偏向右侧壁，完成一次射流切换，形成了稳定的周期性振荡射流。结合图4 可知，低压涡流区分布在壁面和主射流之间，振荡腔内左右两侧的压差驱动主射流偏转。

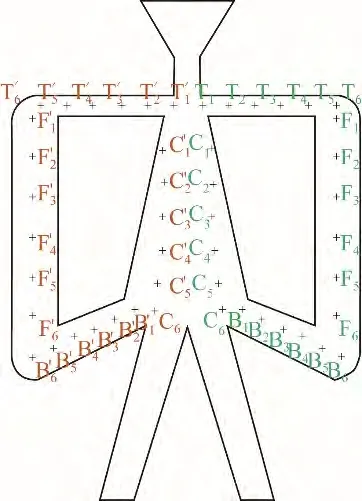
图5 振荡器模型及压力监测点分布Fig.5 Fluidic geometry and pressure measurement locations

图6 ΔP随时间变化的情况Fig.6 ΔP varied with time at various locations

3.2 内部压差变化规律

通过振荡器中间平面的速度云图和压力云图可以定性地看出振荡器内部的振荡过程，但是无法定量化描述振荡过程。为定量化描述振荡器内部流场的流动过程，在数值模拟计算过程中，通过监测振荡器内部特征点和特征面上的流动特性，进而定量化描述振荡器内部的流动过程。

在振荡器内部设置若干对称点，通过监测各对称点的压力变化定量描述振荡器内部的压力变化。在振荡器振荡腔的z=4 中间平面设置了T1～T6和T′1～T′6、F1～F6和F′1～F′6、C1～C6和C′1～C′6、B1～B6和B′1～B′6四组对称点，具体位置如图5所示。

通过fluent 三维模拟计算得到了各对称点处的压力变化，C1～C6和C′1～C′6、T1～T6和T′1～T′6、F1～F6和F′1～F′6、B1～B6和B′1～B′6对称点之间的压差变化如图6所示。图6（a）为振荡器振荡腔内对称监测点的压差随时间变化的情况，振荡腔内部流动过程较为复杂，对称点压差呈现周期性变化，振荡频率与振荡器频率一致。结合图4 压力云图可知，振荡腔入口处的压力变化范围较小，顶部区域的最大压差约为1.4 kPa，而底部区域的最大压差约为2.5 kPa，随着振荡腔内壁侧低压区范围的不断增大和下移，相应监测点的压差不断增大，印证了低压涡流区的存在和迁移，反映出振荡腔内部的流体附壁切换过程是由柯恩达效应和低压涡流区共同作用的结果。图6（b）、（c）、（d）为反馈回路对称监测点的压差变化，最大压差均约为2.1 kPa，由图可知，对称点的压力呈周期变化，且同时达到最大值和最小值，两点的振荡性质相同，其变化规律和振荡器的振荡频率一致。图6（b）为反馈回路出口段对称点的压差，图6（c）为反馈回路中段对称点的压差，图6（d）为反馈回路入口段对称点的压差，随部分流体流入反馈回路，三组对称点压差依次达到峰值，反映出振荡器反馈回路中存在流体的回流过程。

3.3 内部质量流率变化规律

为定量描述振荡器内部的流动情况，在三维振荡器模型里监测了通过面1 和面4、面2 和面5、面3和面6 三组对称平面的质量流率情况，具体位置如图7所示。

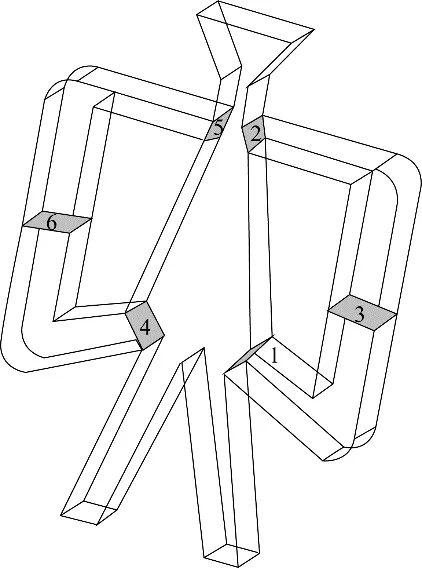
图7 振荡模型及质量流率监测面分布Fig.7 Fluidic geometry and mass flow rate measurement locations

如图8 所示，通过振荡器内部监测面1、2、3（4、5、6）流体的质量流率是守恒的（±仅代表流向），且通过各截面的质量流率呈现周期性变化，其频率与振荡器振荡频率一致。结合图3流场的速度云图和图4 的压力云图可知，在t=5.61 s由于主射流向右侧偏转，不断有流体流入右反馈回路中，使得通过面1和面3 的质量流率达到峰值，流体通过反馈管全部回流至振荡腔，面2的质量流率也随后达到峰值，流入低压涡流区，使得主射流的附壁平衡被打破，主射流向左侧偏移。随着低压区的不断增大下移，卷吸了大量流体，使得流入右侧反馈回路中的流体减少，在t=5.71 s 射流附壁至左侧壁面时，通过面1 和面3 的质量流率达到最小值，面2 随后达到最小值，完成一次射流的附壁切换。左侧反馈回路的流动过程与右侧反馈回路相反，由于柯恩达效应和低压涡流区的共同作用使得振荡器产生了稳定的周期性振荡。

4 结 论

数值模拟采用三维计算模型，得到了振荡器内部流场的速度分布、压力分布和质量流率变化。在计算模型中所监测的四组对称点压差和三组对称面质量流率变化具有良好的周期性和稳定性，有效地反映了振荡器内部的流动特性。射流附于一侧壁时，非附壁侧出现低压涡流区，低压涡流区分布在壁面和主射流之间，振荡腔内左右两侧的压差会驱动主射流偏转，同反馈回路的流体共同作用使得振荡器产生稳定的周期性振荡，得出射流周期性振荡是柯恩达效应和低压涡流共同作用的结果。