基于因果分析的烧结生产状态预测模型
2021-04-09李浩然邱彤
李浩然,邱彤
(1 清华大学化学工程系,北京100084; 2 工业大数据系统与应用北京市重点实验室,北京100084)
引 言
烧结单元是高炉炼铁系统的重要一环,其生产水平的高低直接决定了供给后续高炉生产的烧结矿的质量[1-2]。经验表明,生产的烧结矿中铁含量(TFe)降低1%,高炉燃料比率增加2%,而高炉产量下降增加3%[3],因此烧结单元生产的烧结矿质量与炼铁过程的生产效益紧密相关,维护烧结机的健康工作状态至关重要。通过在某钢铁企业调研过程发现,在实际生产过程中的烧结机状态维护主要是通过手动调节来完成的,具有随意性和滞后性的缺陷。为了改善这一问题,需要针对烧结过程建立模型,对生产状态进行提前判断,从而为现场操作工的操作提供可靠指导。
典型的烧结过程由配料、混合、进料、点火、卸料、破碎和筛选等步骤组成。首先各种铁矿石、烧结返矿、焦炭和熔剂等根据设计方案配比混合,然后进料在移动小车上形成均匀烧结床层。接下来点火器点燃床的表面,在此期间移动小车下方的鼓风机通过抽风的方式在床层下方的风箱内产生负压,由于床层内部含有焦粉和煤粉,点火之后床层在燃料、空气和合适的温度下继续发生自燃,随着台车逐渐向烧结机尾端移动,燃烧不断向下发展[4]。最终使得原料矿粉逐步形成具有一定粒度的烧结矿,作为铁料进入到后续的高炉炼铁生产过程中。
烧结过程具有以下两个特点。
(1)时滞性。一方面,烧结系统中过程变量的变化与其对其下游变量产生影响之间存在时间间隔,称为机制时滞。机制时滞随着传播路径的不同而会有所差异,体现出多时间尺度特征。另一方面,对于生产过程中的同一批原料,由于不同变量测量的时间不同,因此会产生技术时滞。在针对同一批料的变量测量中,传感器分别在t0、t1、t2和t3时刻测量了焦粉比例、一混加水量、点火温度和终点温度这四个变量,这四个时刻之间的不同时间间隔即为不同的技术时滞。这两类时滞的存在使得烧结系统变量之间的影响呈现明显的滞后。
(2)非线性。在烧结过程中涉及的化学反应和物理变化通常处于动态平衡中。在这种状态下,烧结床内部发生一系列化学和物理变化的过程中能量和质量保持平衡,系统处于稳态[5]。烧结过程中除了发生焦炭燃烧、石灰石分解、白云石分解、铁氧体系变化和含硫成分脱除等一系列化学变化外,还存在二维三相复杂传热传质关系,因此烧结系统变量之间呈现明显的非线性关系特征。
由于烧结过程时滞性和非线性这两大特点,虽然现有一些利用机理模型对于烧结过程进行模拟的方法,如姜丽娟[6]建立了基于烧结过程的传热、传质关系的二维模型,以此来获得量热法中漏风前的气体温度值准确率达91.3%。Zhou 等[7]提出了预测气体浓度的方法,Cheng 等[8]提出了预测烧结矿的物理质量指标的能力的方法。但是由于烧结过程来料不稳定,生产模式也经常随之变化,因此建立详细的机理模型不仅工作量大,而且往往难以适应生产状态变化。与此对应的是,近年来数据驱动方法得到了学界的关注和研究,如陈伟等[9]使用BP 神经网络预测烧结矿化学组成,尹学等[10]使用GA-PSOBP 神经网络预测烧结终点等,刘加达等[11]分别使用BPNN 和RNN 预测了烧结矿质量,易正明等[12]使用RBF-BP 混合神经网络预测了烧结烟气氮氧化物含量。数据驱动的方法将系统看作黑箱模型,在一些机理难以详尽模拟的系统建模中取得了良好的效果。
因此本文采用结合机理分析和黑箱建模优点的方法,首先利用因果性分析的方法获得烧结过程中的部分机理知识,即烧结变量之间影响的因果关系和作用时间窗口,然后将此知识应用到黑箱模型建模中,建立烧结系统生产状态预测模型。
1 烧结过程因果性分析
1.1 建模变量选取
在烧结过程中,风箱负压能够维持空气从料层表面向下穿过料层到达主风道的压力差,使得料层内部发生充分燃烧,因此风箱负压与穿过料层的气流量、燃烧的程度、烧结的质量紧密相关。风箱废气温度是空气经过燃烧完全穿过料层后的温度,由于在烧结过程中无法直接测量料层的温度,因此风箱内的废气温度作为能够间接反映料层温度的变量显得尤为重要。烧结终点控制是烧结现场操作工调节设备参数的重要目标[13-15],烧结终点是指燃烧深度刚好完全穿透料层时的位置,若烧结终点过于靠后,则会导致料层没有烧透,影响烧结矿的质量,而若烧结终点过于提前,则会导致从烧结终点到烧结机机尾的这段距离内台车篦条温度持续过高,损坏设备,同时导致烧结矿在到达机尾时温度偏低,不利于维持较好的烧结矿质量。由于以上状态变量对烧结机生产状态的重要指示意义,本文选取第14 号风箱(对应于烧结机中部)和第22号风箱(对应于烧结机尾部)的负压和废气温度以及烧结终点的位置和温度共6 个状态变量作为研究目标。
为了准确预测以上6 个关键状态变量(state variables,SVs)的变化趋势,需要分析这6 个变量变化背后的机理。通常来说状态变量的变化与操作变量(operating variables,OVs)和状态变量历史值有关。本文中采用因果分析的手段来分析这种机理,具体来说,一方面通过自相关函数来分析状态变量的自相关性窗口,另一方面通过收敛交叉映射方法来分析操作变量对于状态变量的因果影响及其时间窗口。
1.2 状态变量自相关性分析
烧结生产状态具有一定的自相关性,即前一段时间的系统状态变量会对之后的状态变量产生明显的因果作用,因此有必要对这种自相关性进行分析。自相关函数[16-17](autocorrelation function, ACF)是用来衡量同一序列中不同时间间隔数据间的相关性随时间间隔的变化的指标,其计算方法如式(1)所示:
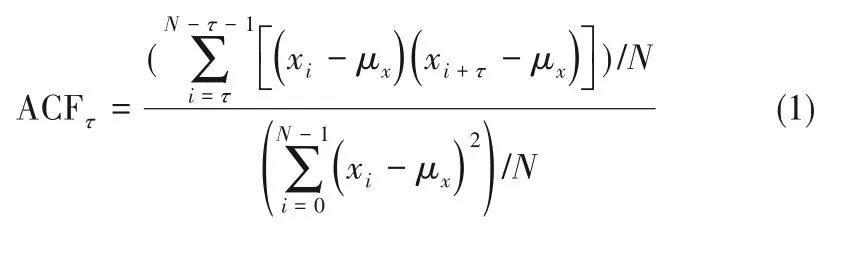
其中,τ是滞后期,μx是序列均值。
选取六个系统状态变量:14 号风箱负压(OV1)、22 号风箱负压(OV2)、14 号风箱废气温度(OV3)、22 号风箱废气温度(OV4)、燃烧终点位置(OV5)、燃烧终点温度(OV6)进行自相关函数分析。结果如图1 所示。可以发现随着时滞期延长,所有六个变量的ACF 值均从1 开始逐步下降,取阈值水平为0.6,对应的平均自相关窗口长度为27 min。
1.3 操作变量对状态变量的因果性分析
变量间因果关系能够揭示系统中各因素之间的因果性,从而能够帮助明确系统中某些变量发生变化背后的机理。变量因果性分析已有许多方法研究,如Bauer 等[18]提出了互相关分析(crosscorrelation analysis, CCA),Granger[19]提出了格兰杰因果关系(granger causality, GC)检验,Schreiber[20]基于信息熵的概念提出了传递熵(transfer entropy,TE),但这些方法存在计算量大[21-22]或只适用于线性或弱非线性系统[23-27]等缺点,不能确保对强非线性系统中的耦合变量进行因果关系的正确识别,而Sugihara 等[28]提出的收敛交叉映射(convergent cross-mapping, CCM)可以克服此问题。McCracken等[29]证明了CCM 算法可用于双向因果性推断,Mønster 等[30]验证了其在噪声数据中的适应性,Luo等[31]进一步发展了CCM 算法以适应化工过程的需要。因此本文采用CCM 方法对于操作变量对状态变量的因果性进行研究。
本文中所使用的CCM方法主要步骤如下:
(1)读取数据并归一化 从数据集中读取两个时间序列变量X =[x1,x2,…,xt]和Y =[y1,y2,…,yt],并按照以下规则进行归一化:

(2)重构流形 按照延时嵌入原则分别重构X和Y的吸引子流形:
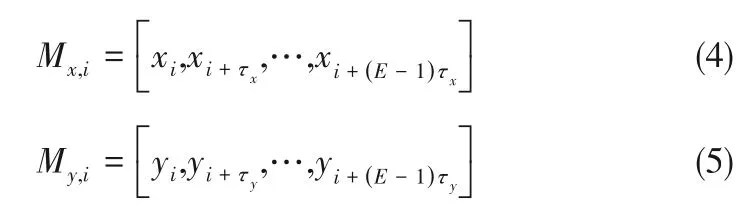
其中i = 1,2,…,N -(E - 1)τ。E 是嵌入维度,τ是时间滞后。
(3)流形预测 在Mx上寻找Mx,i的E + 1 个由近 到 远 近 邻 点 Mx,i1,Mx,i2,…,Mx,iE+1,计 算Mx,i1,Mx,i2,…,Mx,iE+1离Mx,i的欧式距离,得到权重u:
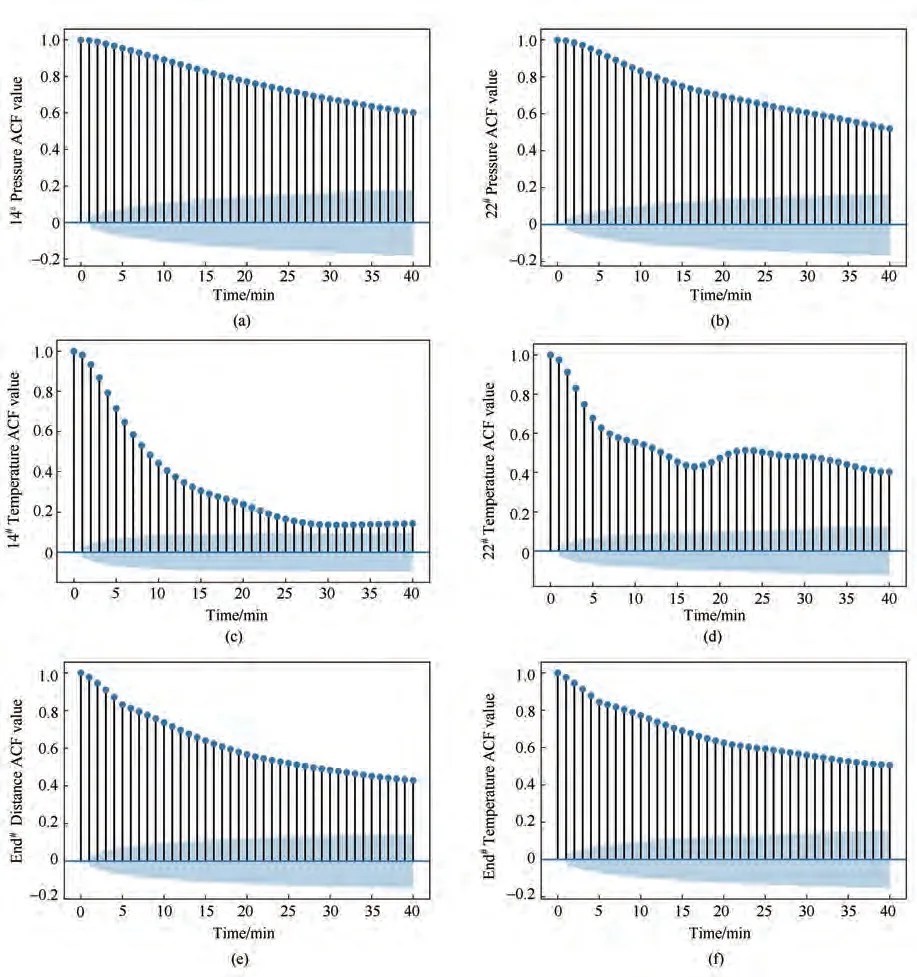
图1 6个状态变量的自相关函数值Fig.1 Autocorrelation values of six state variables
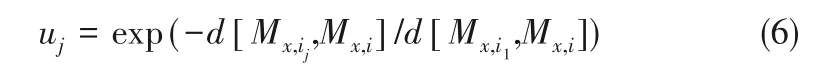
在My上寻找对应的E + 1个点My,i1,My,i2,…,My,iE+1,计算使用Mx,i预测My,i的预测值:
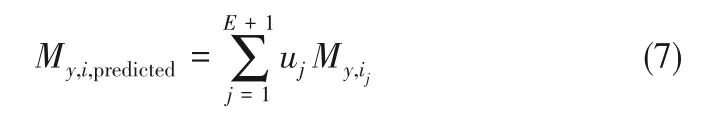
(4)计算收敛交叉映射能力值
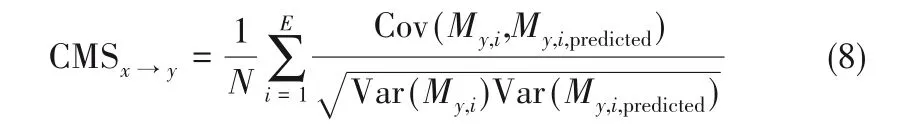
当考虑时滞时,CCM 可以通过数据平移的方法实现[32],即在计算收敛交叉映射能力值时将真实值平移一个滞后期(lag),然后与预测值计算相关系数。
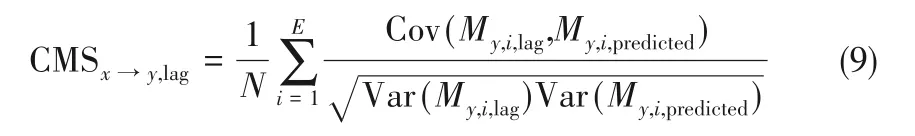
按照时滞算法取CMS 值的最大值作为有时滞情况下的操作变量对状态变量的CMS 值,总结如表1所示。
分析表1 中的数据可以发现1 号主风机频率和2 号主风机频率对于14 号风箱和22 号风箱负压的CMS 值均在0.6 左右,明显高于系统中其他变量的CMS 值,说明风机频率与风箱负压具有强因果关系。这一点也能够从机理上得到解释,即主抽风机抽风的频率决定了风箱负压。

表1 操作变量对状态变量的CMS值Table 1 CMS values of OVs towards SVs
除上述数据之外,表1 中的其他数据均位于0~0.4的范围之内,说明在烧结系统中的数据因果性并不强。这是因为对于实际的工业系统,一方面各过程变量相互之间具有强耦合特征,另一方面由于变量之间的关系复杂,往往变量之间的关系不是直接相关,所以CMS 值会随着传播路径的变长而减小。基于以上两点,将烧结系统中变量因果性的阈值取为0.1,即认为在CMS>0.1时变量之间存在明显的因果关系。
在此阈值水平下,可以认为对于OV1~OV 3构成其原因的变量个数为9 个,对于OV6 构成其原因的变量个数为8 个,对于OV4~OV 5 构成其原因的变量个数为5 个。对于14 号风箱负压和废气温度、22 号风箱负压这三个状态变量,表1 中所选择的9个操作变量均对其构成显著因果关系,而对于22号风箱废气温度,除点火温度、台车速度、圆辊速度、七辊速度CMS 值略低于0.1,其余操作变量均显著。同理对于烧结终点位置,除了料层厚度、B 排点火强度、台车速度、圆辊速度略低,其余也均构成显著因果关系。对于烧结终点温度,除七辊速度外,其余因果关系均显著。从冶金实践来看,料层厚度、圆辊速度和七辊速度与烧结床层的性质相关,点火强度和点火温度与初始燃烧状态相关,台车速度、主风机频率分别对应燃烧时间和风箱负压,均与燃烧相关。综上结合因果分析和机理分析,可认为本文中所选择的9 个操作变量,对于6 个状态变量均构成较好的因果解释性,可以用于后续的预测。
设定样本量为5000,取滞后期为-40~40,嵌入维度E=3,嵌入时滞τ=1,选取9 个操作变量对于状态变量进行CCM 分析。图2 是A 排点火强度(SV2)、点火温度(SV4)、圆辊速度(SV6)和1号主风机频率(SV8)对14 号风箱负压和废气温度的CMS值时滞曲线,可以发现CMS 值在20~40 min 的时滞期内均较高,此后逐渐降低。这一现象说明大部分的操作变量对状态变量的因果关系存在明显的滞后,滞后期为20~40 min,因此可将20~40 min 作为本文选取的操作变量对状态变量影响的因果窗口。结合本数据集对应的冶炼生产实际情况来看,从进料到烧结完成的时间大致为40 min,与此处的因果性窗口较好对应。
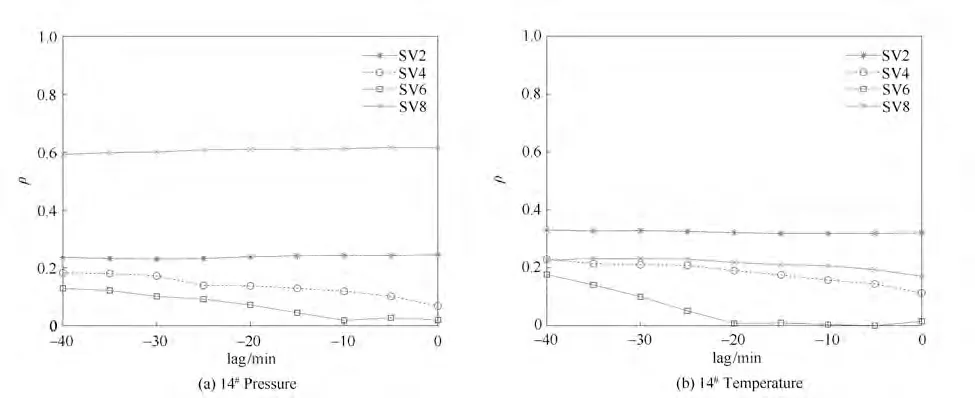
图2 CCM算法时滞分析结果Fig.2 CCM time lag analysis result
2 烧结生产状态预测模型
2.1 模型结构
烧结状态预测模型如图3所示,共分为两层:因果分析层和神经网络层。因果分析层是通过数据因果性分析的方法获得关键操作变量集、自相关窗口和因果影响窗口。具体来说,通过收敛交叉映射的方法从过程操作变量中选取与状态变量有显著因果关系的操作变量构成关键操作变量集,如图3中OV1~OV9 所示,这些操作变量中蕴含了未来状态变量的变化趋势,可以作为后续神经网络的输入。除此之外,收敛交叉映射还可以得到操作变量集对状态变量影响的时间窗口,如图3中OV对应的黑色和深灰色色块所示,这一窗口包含了变量间作用的时滞信息。自相关函数分析能够对状态变量的自相关性进行分析,从而获得状态变量的自相关窗口,如图3 中SV 对应的黑色和深灰色色块所示,这一窗口包含了变量自身作用的时滞。
神经网络层中接收这些信息作为学习到的知识作为输入,然后进一步学习输出关键状态变量的预测值。神经网络层采取具有全连接层的人工神经网络作为基本模型,采用开源的pytorch 库构建神经网络。优化器选择torch.optim.Adam(),学习率是10-3。损失函数选择torch.nn. L1Loss(),该损失函数对应的是平均绝对误差(mean absolute error,MAE),数学表达如式(10)所示:
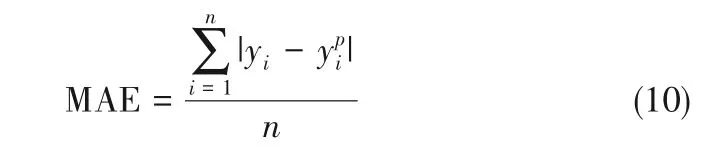
对于隐藏层,采用的激活函数是线性整流函数(ReLU 函数),该函数在x<0 时的取值为0,在x>0 时的取值为x,其数学表达如式(11)所示:

2.2 模型预测结果及精度分析
使用此模型对6 个状态变量预测结果如图4 所示,可以发现对于6个状态变量,使用具有因果分析层和神经网络层的生产状态预测模型均能较准确地预测其变化趋势。
将模型的预测精度总结见表2,可以发现对于状态变量的预测平均相对误差介于0.5%~3.1%之间,其中对于第14号风箱负压的预测平均相对误差是0.51%,而对于第14 号风箱废气温度的预测平均相对误差是3.07%,较精准地预测了状态变量的变化趋势,从而为现场操作工提前预知烧结机生产状态变化,及时调整操作变量提供了参考。
3 结 论
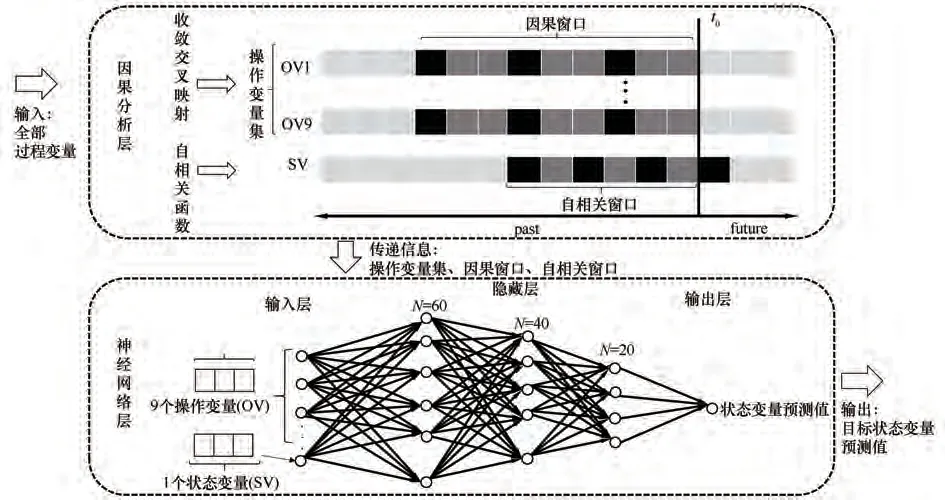
图3 烧结生产状态预测模型框架Fig.3 Scheme of sintering production state prediction model
本文融合因果性机理和神经网络黑箱模型,建立了烧结生产状态预测模型。因果分析层使用自相关函数分析和收敛交叉映射的方法分别获得了烧结状态变量的自相关窗口、关键操作变量集及其对状态变量的因果性影响窗口。神经网络层采用误差反向传播神经网络,接受因果分析层的输入并对6 个关键状态变量进行预测。经过工业数据测试,该模型能够在3.1%的误差范围内对烧结生产状态实现较精准的预测,从而能够根据过程数据初步预判烧结机生产状态的变化趋势。为后续进一步研究烧结机生产状态调整策略,实现对现场操作工的指导提供了基础。
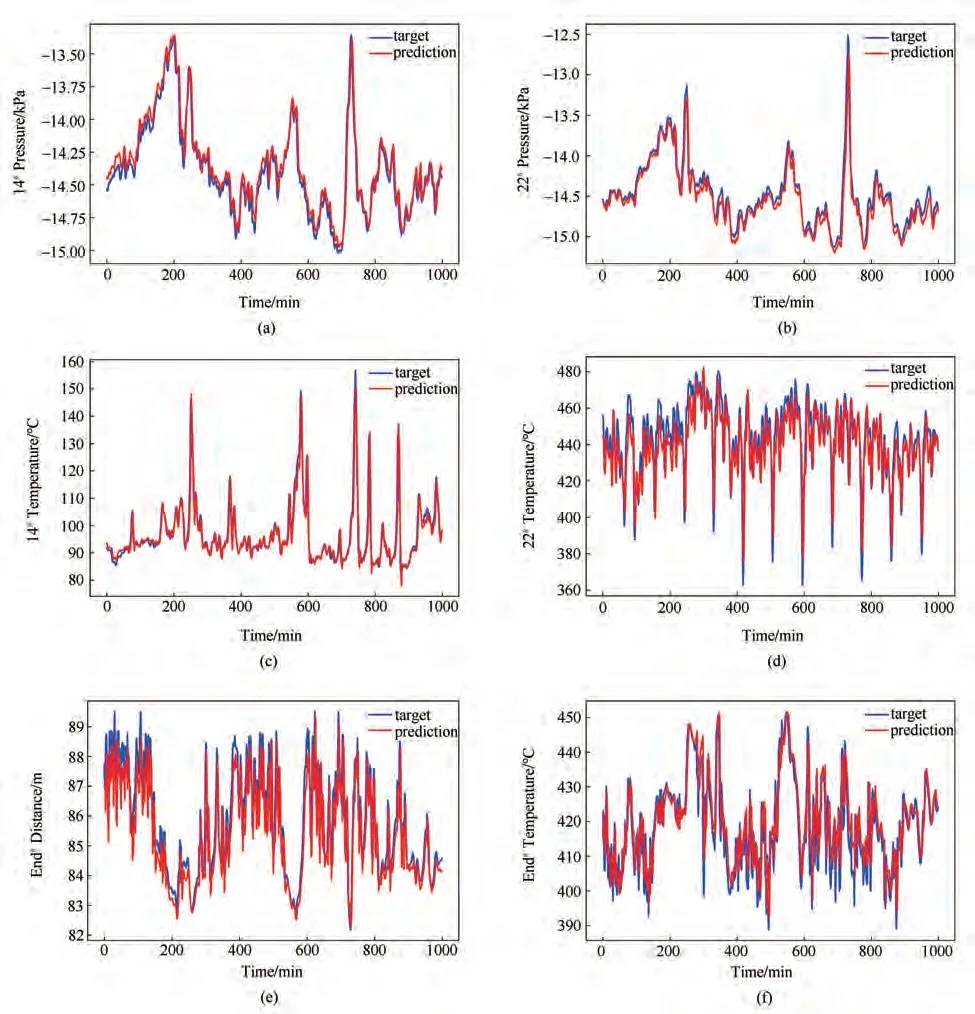
图4 烧结生产状态预测结果Fig.4 Prediction results of sintering production state
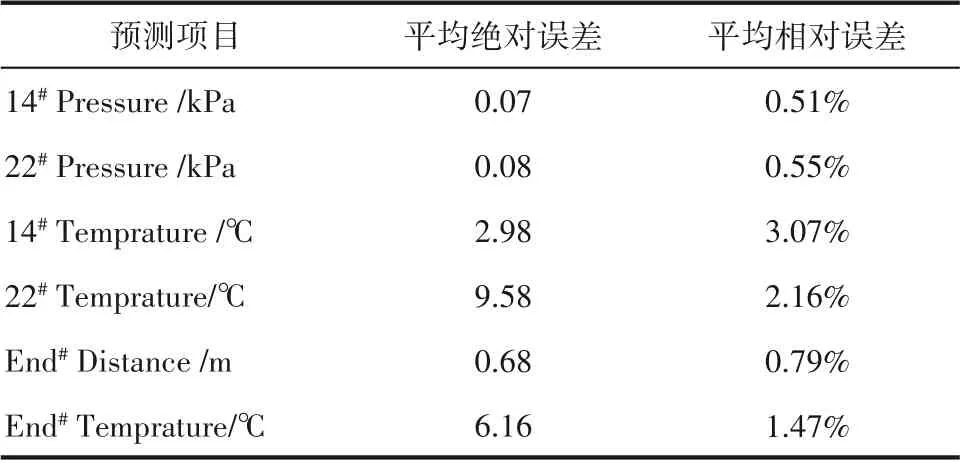
表2 烧结生产状态预测模型预测误差Table 2 Prediction errors of sintering production state prediction model
符 号 说 明
CMS——收敛交叉映射能力值
MAE——平均绝对误差
OV——操作变量
SV——状态变量
