Deformation response of roof in solid backfilling coal mining based on viscoelastic properties of waste gangue

Peng Hung,Jixiong Zhng,*,Xingjie Yn,Anthony John Spener Spering,Meng Li,Shiwei Liu

a School of Mines,China University of Mining and Technology,Xuzhou 221116,China

b State Key Laboratory of Coal Resources and Safe Mining,China University of Mining and Technology,Xuzhou 221116,China

c School of Mathematics,China University of Mining and Technology,Xuzhou 221116,China

d National Engineering Laboratory For Surface Transportation Weather Impacts Prevention,Broadvision Engineering Consultants,Kunming 650041,China

Keywords:SBM Fractional order Thin plate Time factor Viscoelastic foundation Roof deflection and bending moment

ABSTRACT Solid backfill mining (SBM) is a form of green mining,the core of which is to control and minimize the deformation and movement of strata above longwall coal mines.Establishing a mechanical model that can reliably describe roof deformation by considering the viscoelastic properties of waste gangue is important as it assists in improving mine designs and reducing the environmental impact on the surface.In this paper,the time-dependent deformation characteristics of gangue under different stress levels were obtained by using lateral confinement compression,that reliably represents the compaction of goaf.The viscoelastic foundation model for gangue mechanical response is different from the traditionally used elastic foundation model,as it considers the time factor and viscoelasticity.A mechanical model using a thin plate on a fractional viscoelastic foundation was established,and the roof deflection,bending moment,time-dependent,viscous and other characteristics of SBM were included and analyzed.Compared with the existing elastic foundation model,the proposed fractional order viscoelastic foundation model has higher accuracy with laboratory data.The plate deflection increases by 50.9% and the bending moment increases by 37.9% after 100 days,which the elastic model would not have been able to predict.

1.Introduction

Solid backfill mining (SBM) has received much attention in recent years due to its environmental benefits[1-3].SBM can solve a series of environmental problems caused by caving mining,such as strong ground pressure,intense overburden movement,serious groundwater loss,surface deformation,and ecological deterioration as shown in Fig.1 [4,5].This method places solid backfilling materials (gangue,fly ash,aeolian sand,loess,mineral waste residue,etc.) into the goaf behind the working face by using the surface solid backfilling feeding system and underground backfilling material transportation system.The movement of the overburden rock strata and the surface deformation are highly related to the mechanical response of the backfilling material in the process of rock stratum bending[6,7].In the whole process of SBM,however,the final backfilling effect depends on the compaction characteristics of backfilling materials and the movement characteristics of overlying rock stratum.

The mechanical properties of backfilling materials have been studied in recent years.Meng et al.[8]used WAW-1000D electro-hydraulic servo universal machine to conduct compaction testing of crushed sandstones,which was heated to different temperatures.They analysed the influence of temperature on the stress-strain relationship,porosity changes,and deformation mechanisms during the compaction of crushed sandstones.Zhou et al.[9]studied the mechanical and microstructural properties of refuse mudstone-slag-red mud.The tests of unconfined compressive strength,Brazil tensile strength,and microstructure were carried out and analyzed.Qi and Fourie [10]reviewed the cemented paste backfill experimental techniques and progress design.Li[11]investigated the compaction properties of five common materials used in the SBM,obtaining stress-strain,bulk-ratio-stress,and strain-time relationships for each of them.Deng et al.[12]studied the time-dependent rheological behavior of cemented backfill mixture and proposed that samples with finer particle sizes have a lower apparent maximum packing density compared to those with larger particle sizes.Zhao et al.[13]investigated the effects of binder type,content,water chemical properties and content,and temperature,on the rheological properties of cemented paste backfill.Li [14]studied the damage evolution of the backfill material and its host rock behaviour under three-dimensional dynamic loading.The mechanical properties of the abovementioned backfilling materials mainly focus on strength,compaction characteristics,and deformation characteristics.Due to the fact that gangue is a loose material and experimental equipment limitation of pressure,there are few researches on the rheological properties of gangue materials.However,the rheological properties of gangue also need to be studied in depth because of the ground control and ecological protection superiority of SBM that can be disclosed.

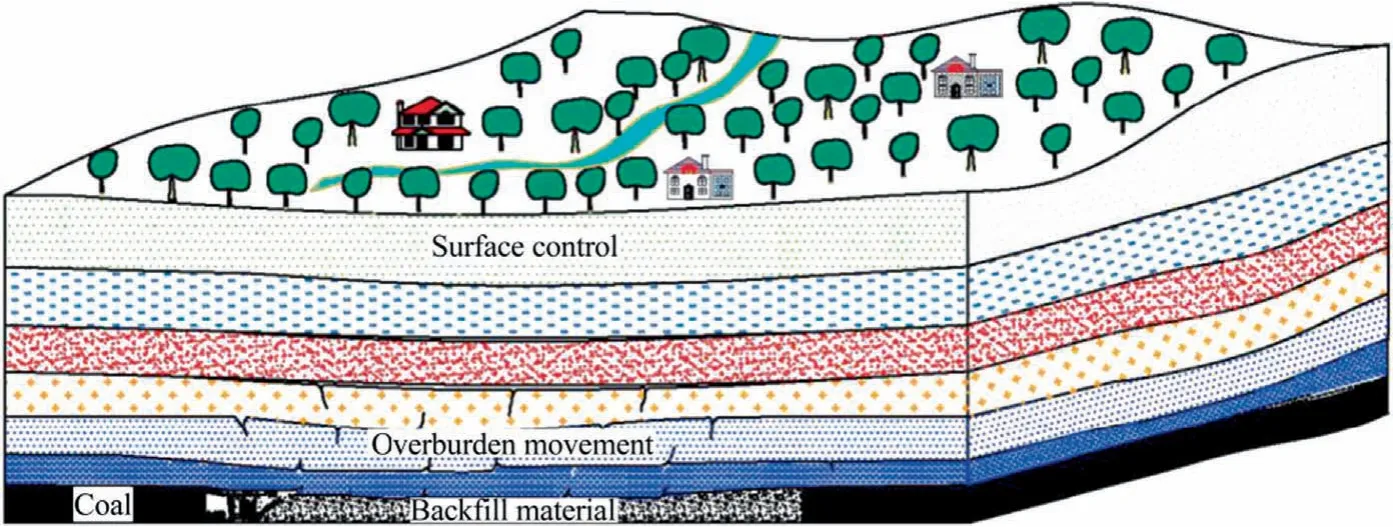
Fig.1.Ground control in SBM.

The mechanical roof models using SBM have been based on the properties of backfilling materials and developed in recent years.The SBM model of the thin plate was established by using the Ritz method in backfill mining.The result shows that the maximum roof subsidence and maximum tensile stress appear at the center of the roof [15].A mechanical model to determine the roof filling control mechanism was established and the stability of the lower roadway in a small pit goaf was analysed[16].Dong et al.[17]proposed an analytical model based on energy conservation to investigate the stability of the surrounding rock mass due to excavation by using a complex variable method.The triaxial creep experiments have been conducted on Gachsaran salt samples under various temperatures and differential stresses [18].Li et al.[19]established a mechanical model of the SBM roof by using the theory of thin plate on an elastic foundation.Zhang et al.[20]established a mechanical model for recovering retained room coal pillars through solid backfilling by using the elastic foundation beam and analyzed the stability of the coal pillars.However,the compaction characteristics of backfilling materials cannot be accurately reflected in the above elastic mechanical roof models.This is because elastoplasticity and/or viscoelasticity response should be taken into account in the constitutive model of solid backfilling materials.In addition,the rheologic properties of backfilling materials have also been ignored in those models.Therefore,a new mechanics model that can accurately reflect the compaction process and time dependence of backfilling materials need to be established to better predict rock stratum movement after SBM.

2.Research status on the fractional viscoelastic foundation

Fractional calculus has been widely applied to structural dynamics problems both in discrete and continuous equations.Rossikhin [21]analyzed the new trends and recent results carried out in the field of fractional calculus application to dynamic problems of solid mechanics,dealing with the study of the dynamic behavior of linear and nonlinear 1DOF systems.Hedrih [22]researched the models and dynamics of coupled systems composed of a number of deformable bodies (plates,beams,or belts)with different properties of materials and discrete layer properties by using three basic models.The above research focuses on the application of fractional calculus for the dynamics of coupled systems,and the solution of quasi-static deflection of the plate on the fractional viscoelastic foundation is not mainly analyzed.

Recent fractional theory innovations have caused considerable interest in the study of fractional viscoelastic foundation [23].Zhu et al.[24]studied the response of the loaded rectangular plate on the fractional viscoelastic foundation.The fractional Kelvin model(FKM)was adopted as the fractional viscoelastic foundation.The viscoelastic solution of this problem was obtained by using the elastic and viscoelastic correspondence principle and Laplace transform.The results of calculation examples show that the fractional viscoelastic model is more adaptive than the classical viscoelastic model.Zhang et al.[25,26]proposed a fractional generalized Kelvin model (FGKM) to investigate the timedependent behavior of a simply supported rectangular plate on the viscoelastic foundation.The solutions of plate response under uniformly distributed load were derived by involving Laplace transforms and correspondence principle.The long-term performance of the plate can be accurately simulated by varying the values of the fractional differential order and the viscosity coefficient.The plate deflection,bending moment,and foundation reaction can be captured even over many decades of time.The fractional derivative of the deflection equation of the rectangular plate on the viscoelastic foundation under load was established by using the above two methods in the literature [27].Kou and Bai [28]investigated the dynamic response of rectangular plates on the twoparameter viscoelastic foundation with fractional derivatives and FKM also was selected as the viscoelastic foundation.The dynamic equations of elastic and viscoelastic rectangular plates with fouredges that are simply supported were solved with the Galerkin method and the segmented numerical method.The attenuation speed of the displacement response increases with increase in viscosity coefficient,horizontal shear coefficient and modulus.Cai et al.[29]proposed a fractional Pasternak-type foundation model to characterize the time-dependent properties of the viscoelastic foundation.The viscoelastic foundation actually was the Abel dashpot (AD).The influence of fractional order on the deflection and bending moment and the difference between fractional Pasternak and fractional Winkler model were discussed in this paper.According to the above literature research results,the fractional AD has certain viscoelastic characteristics in the fractional viscoelastic foundation model.Compared with the integer-order model,fractional foundation model has higher accuracy and certain advantages in local data fitting and unsmooth data fitting.However,the previous model parameters have not been verified by laboratory or field tests.The static or dynamic response of viscoelastic foundation plate cannot be very accurate.Moreover,these models are focused on the solution of the loaded plate on the viscoelastic foundation,whereas in the plate model of SBM,there are few studies on response analysis of the viscoelastic foundation.

In this paper,a fractional creep model of backfilling material is established and verified based on the experimental data of lateral confinement compression of gangue.This can describe the relationship between strain and time more accurately than the other four previously discussed fractional viscoelastic foundations.A new mechanical model of the thin roof in SBM based on the fractional viscoelastic foundation is established.The deflection and bending moment equations of the thin plate model on the fractional viscoelastic foundation are derived.The time-dependent,viscous,and order characteristics of the fractional foundation are also analyzed.

3.Creep characteristics of solid backfilling materials

Five sets of short duration,constant load with lateral confinement compression of the waste rock under different stress states were designed and tested in the laboratory.The deformation characteristics and time-dependent characteristics of backfilling materials during compaction were obtained.This is well described by the relationship between strain and time in the laboratory,which provides a theoretical basis for the selection of basic components of the creep model.

3.1.Sample characterization and experimental equipment

The main lithology of gangue materials is mudstone with a particle size range of 0-30 mm,an average density of 1420 kg/m3and a moisture content of 0.4% from Pingdingshan Coal Mine.The gangue size distribution is shown in Table 1 by using the standard size griddle.The X-ray diffraction (XRD) results show that mudstone mainly consists of 37.31% quartz,34.62% kaolinite,11.63%illite,2.01% chlorite,1.25% feldspar,and other minerals.

The porosity content of gangue in a steel barrel (φ) can be calculated using Eq.(1) [12].

where mbis the total weight of the gangue in kg;d the steel barrel’s inner diameter in m;hbthe stack height in m;and ρsthe density of gangue in kg/m3.

Fixing the weight of gangue (10 kg) and measuring the filling material height 5 times in compaction cylinder,using Eq.(1) the porosity of gangue grain averaged 41.35%.

The YAS-5000 electro-hydraulic servo-controlled rock mechanic test system,manufactured by Changchun Kexin Test Instrument Company,was used to test the lateral confinement compression experiment of gangue [16].The maximum test force of the testing machine is 5000 kN,the maximum stroke is 200 mm,and the oil source is controlled by the MOOG servo valve,which can determine the long-term constant load application.The compacted steel barrel is a cylindrical compacted steel barrel designed by the authors.The steel barrel’s inner diameter is 250 mm,height is340 mm,yield limit is 235 MPa,and safety factor is 1.47,all of which meet the requirements of the experiment.

Table 1 Gangue size distribution.

3.2.Compaction and time-related characteristics of gangue

The relationships between strain and time,deformation rate and time of gangue under five different axial pressure are shown in Fig.2.

As shown in Fig.2,the deformation of gangue is not linear with time in lateral confined compression tests of gangue.With the increase of axial pressure,the deformation of gangue increases gradually;in the process of lateral confined compaction of gangue,the deformation of gangue can be divided into two stages i.e.deceleration deformation and stable deformation.The deformation rate tends to be stable after 30 min.

4.Mechanical roof model of the thin plate in SBM based on fractional order viscoelastic foundation

The existing mechanic roof model of SBM mainly uses the elastic foundation beam and elastic foundation thin plate,that represents gangue backfilling material as an elastic material.It can be seen from Fig.2,however,the relationship between gangue deformation and time is not linear.A new roof model was established based on the deformation path of gangue in long-term compaction.

4.1.Abel dashpot (AD)

AD is a component derived from the integer-order creep element,as shown in Fig.3a.

AD’s stress and strain can be expressed as

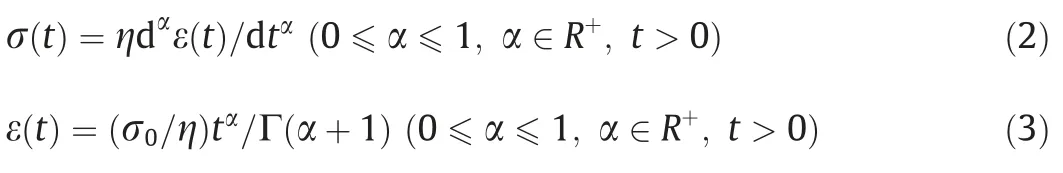
where α is the fractional order;t the time in h;η the coefficient of viscosity;σ the stress in MPa;σ0the constant stress in MPa;ε the strain;and Γ the Gamma function.

When α=1,Eq.(2)becomes σ(t)=ηdε(t)/dt,then AD is an integer element,describing the viscous fluid characteristics of rock;when α=0,Eq.(2) becomes σ(t)=ηε(t),then AD is an elastic element,reflecting the elastic characteristics of the rock.

4.2.Fractional viscoelastic foundation model (FVFM)

4.2.1.Fractional Maxwell model (FMM)

The FMM is composed of an elastic element and a fractional AD with a series relationship,as shown in Fig.3b.

The constitutive relation of each element in FMM is as follows.

where ε1and ε2is the elastic element and AD strain,respectively;E the elasticity modulus of elastic element in MPa;and Dα the fractional differential operator.

The series relationship is shown as Eq.(5).

Substituting Eq.(4) into Eq.(5) and applying Laplace transformation,Eq.(6) can be obtained as follows.

where s is the transform variable;andthe Laplace transform.

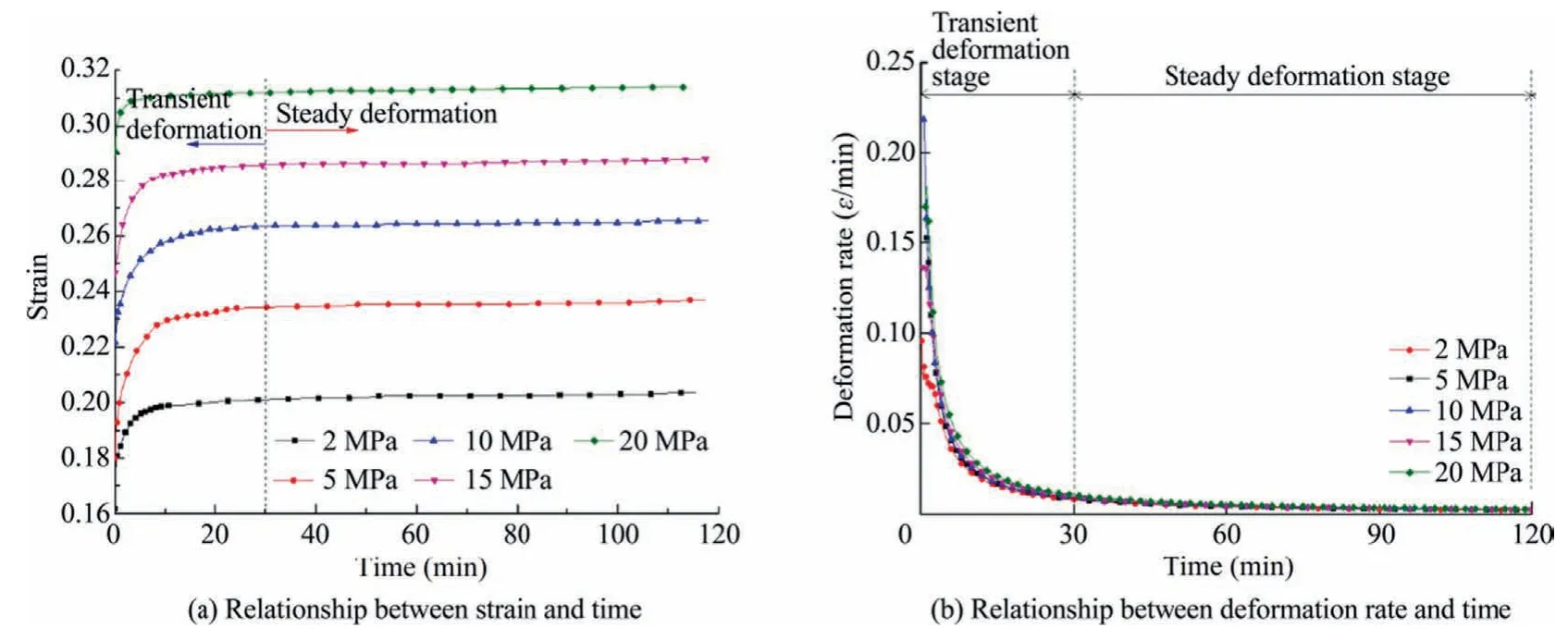
Fig.2.Time-related characteristics of gangue.

Fig.3.Five basic fractional models.

The constitutive relation of the Maxwell model is obtained by inverse Laplace transform of Eq.(6).

When σ(t)=σ0,the creep relation of the Maxwell model can be obtained by Laplace transform and inverse transform of Eq.(7).

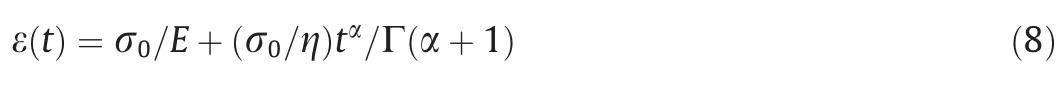
4.2.2.Fractional Kelvin Model (FKM)

The FKM is composed of an elastic element and a fractional AD with a parallel relationship,as shown in Fig.3c.According to the Laplace transformation and parallel relation of which the FKM follows,the FKM equation can be written as follows:

where E2is the elasticity modulus of elastic element in MPa.

The constitutive equation of FKM can be obtained by Laplace inverse transformation on both sides of Eq.(9).

When the stress is constant,Laplace transformation and inverse transformation are performed on both sides of Eq.(10),and then according to the Mittag-Leffler equation,the creep relation of FKM can be obtained as follow.

where Ea,a+1is the Mittag-Leffler function.

4.2.3.Fractional generalized Kelvin model (FGKM)

The FGKM is composed of an elastic element and an FKM,as shown in Fig.3d.According to Eqs.(4)and(11),the creep relation of FGKM can be obtained as follow.

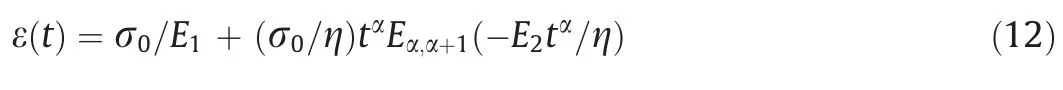
4.2.4.Fractional Poynting-Thomson model (FPM)

The FPM consists of FMM with elastic components in parallel connection,as shown in Fig.3e.According to the Eqs.(1),(7),and (8),by using the parallel connection and Laplace transformation,the following result can be obtained.

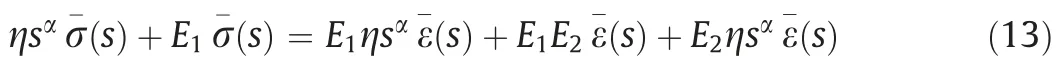
The constitutive relation of FPM is obtained by inverse Laplace transform of Eq.(13) [30].

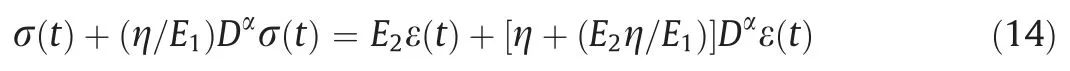
When σ(t)=σ0,Eq.(15) can be obtained by the Laplace transform of Eq.(14).

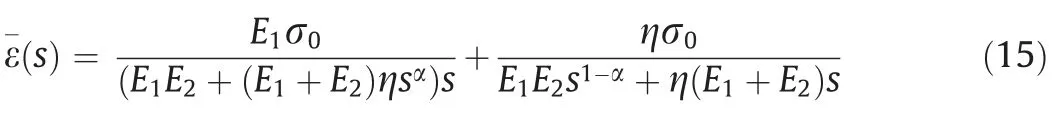
Eq.(15)can be changed into the form of Mittag-Leffler function.

By performing inverse Laplace transform of Eq.(16) and introducing the Mittag-Leffler function,the creep relation of FPM can be obtained as follows.

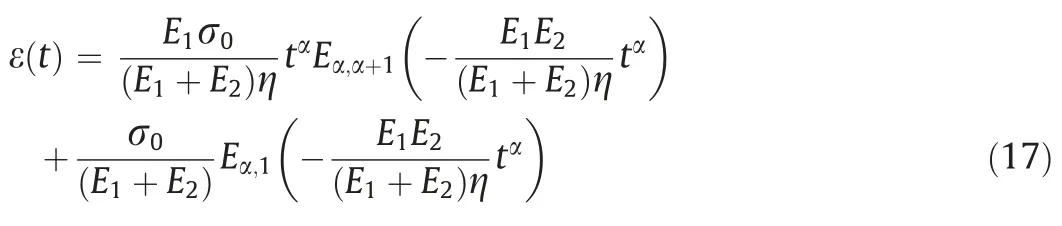
4.3.Three-dimensional model of FVFM and comparison

4.3.1.Three-dimensional model of FVFM

The expression of generalized Hookes law in three-dimensional form is as follows.

where σmis the first invariant of the stress tensor in MPa;Sijthe deviatoric stress tensor in MPa;eijthe deviatoric strain tensor;K the bulk modulus in GPa;and G the shear modulus in GPa.

Usually,rock is in the three-dimensional stress state,the spherical stress tensor will cause the volume deformation of the element without changing its shape,and the deviatoric stress tensor causes element shape change without volume change.The expressions of stress state (σij) and strain state (εij) are as follows.

where εmis the first invariant of strain tensor;σmδijthe spherical stress tensor in MPa;and εmδijthe spherical strain tensor.

Therefore,the strain expression of elastomeris

In elastic state,assuming that spherical strain tensor εmδijand deviatoric strain tensor eijare respectively related to the deviatoric stress tensor Sij,therefore,the strain expression of fractional viscoelastic bodyis given by

Base on Eqs.(20)and (21),referring to[31],the creep equation of AD,FMM,FKM,FGKM,and FPM in the three-dimensional state can be obtained as follows respectively.

where εA(t),εM(t),εK(t),εKG(t),and εT(t) is the three-dimensional strain of the AD,FMM,FKM,FGKM and FPM,respectively;and G1and G2the shear modulus of the FPM respectively in GPa.

The relationship between confining pressure and axial pressure is as follows.

where λ is the coefficient of horizontal pressure;and σ1,σ2,and σ3the principal stress in MPa.

The three-dimensional creep equation of FVFM is as follows.

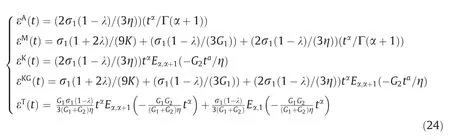
4.3.2.Parameter identification and model comparison

Eq.(24) can be approximated by the series expansion,in order to obtain a reasonable solution without losing accuracy,taking the first ten classes to fit the test data of gangue under different loads.The fitting comparison of AD,FMM,FKM,FGKM,and FPM under different loads are shown in Fig.4,the parameters and R square of these models are shown in Table 2.

From Fig.4 and Table 2,it can be seen that the FPM is more consistent with the test data and has a higher accuracy because of its R2of consistently over 0.94 compared to AD,FKM,FMM,and FGKM of which average R2values are 0.58,0.58,0.83,and 0.83,respectively,showing a low correlation in both decelerating stage and steady stage.Therefore,the FPM model should be,with its higher accuracy with the gangue creep property,selected as the most accurate viscoelastic foundation model.

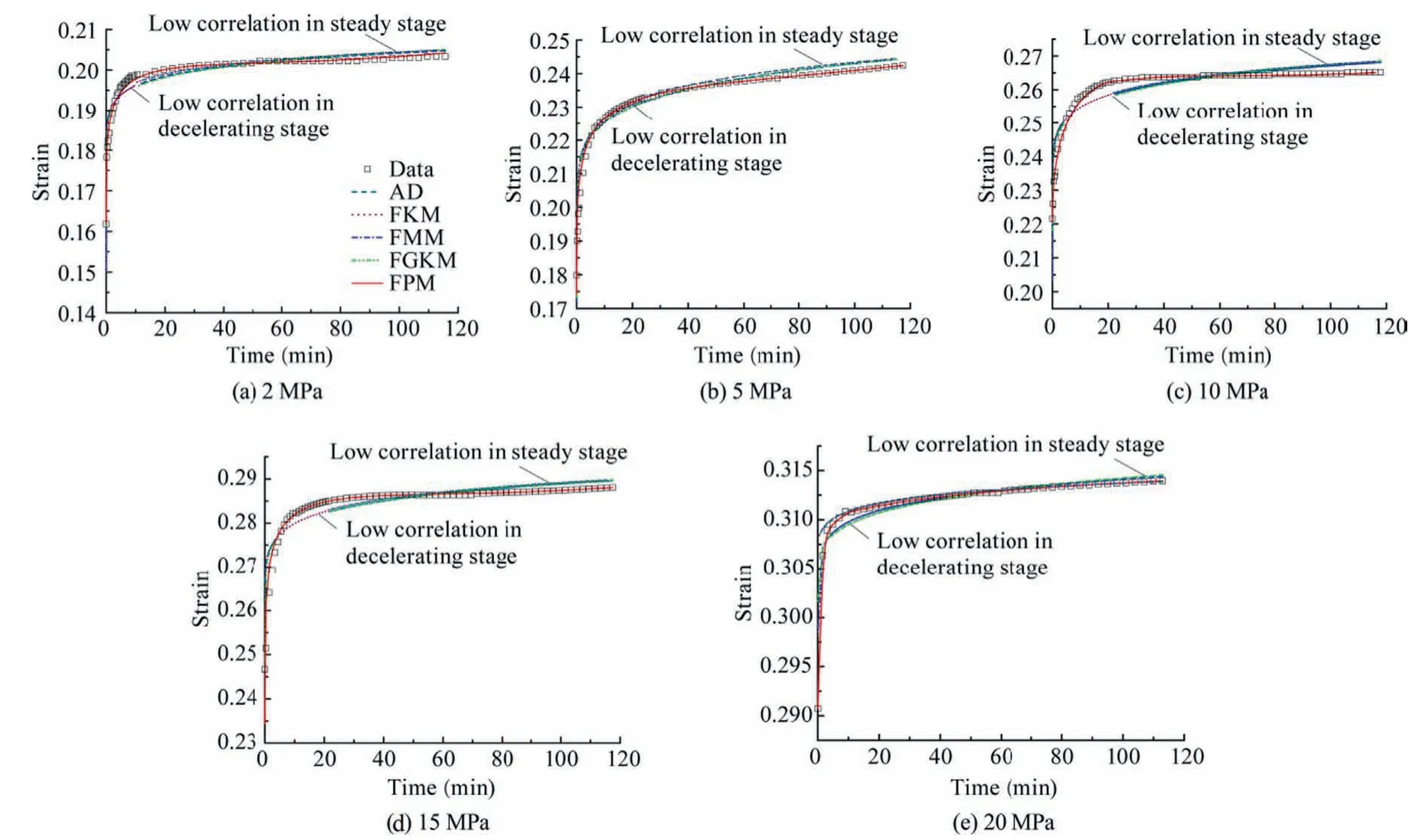
Fig.4.Fitting curve of gangue creep data with five creep models.

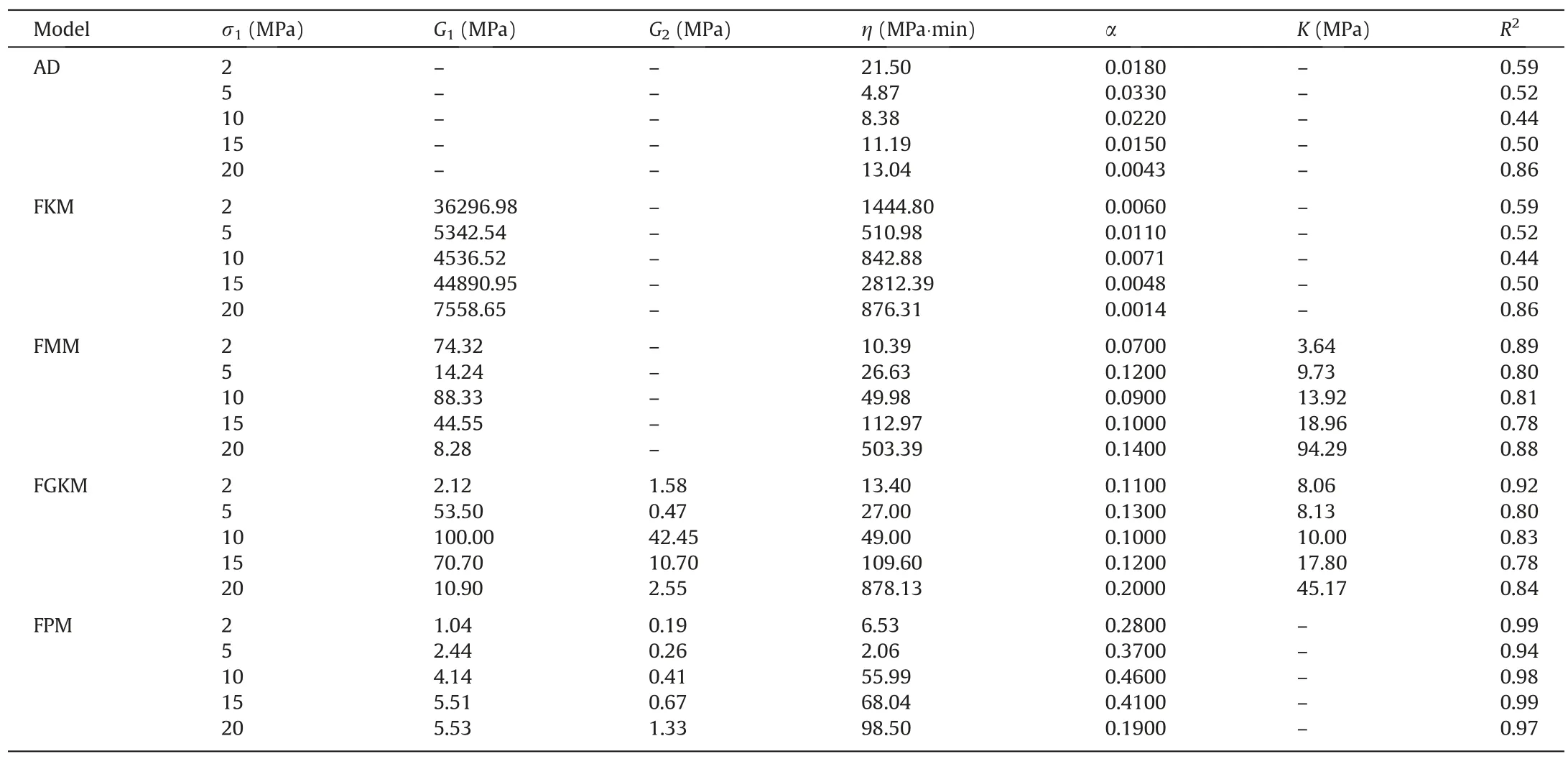
Table 2 Parameters and R square of the five creep model.

4.4.Mechanic model of the thin plate on the fractional viscoelastic foundation

In SBM,the main roof,the thickness h in m can be regarded as a clamped thin plate supported by the upper strata,q(x,y),and the lower elastic foundation,p(x,y).Since the overlying rock stratum will not form a caving zone after SBM,the boundary conditions of the roof can be simplified as four-sided fixed support [16,32].The working face advance direction is set up as positive x-direction,length of a in m,the dip direction set up as positive y-direction,length of b in m,and the vertical direction set up as positive z-direction,as shown in Fig.5.

4.5.Solution of the thin plate on fractional viscoelastic foundation

4.5.1.Solving thin plate on elastic foundation

The differential equation of the bending surface of the elastic thin plate is proposed as shown in Eq.(25).

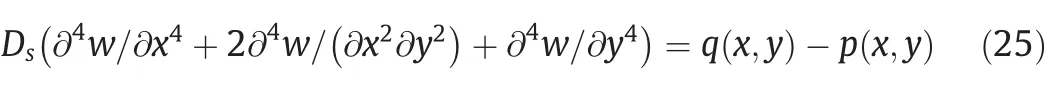
where w is the deflection of plate in m;Dsthe flexural rigidity of the plate,Ds=E0h3/(12(1 -μ2));E0the elasticity modulus of elastic element in MPa;h the height of plate in m;and μ the Poisson’s ratio.

The definition of foundation reaction force can be written as Eq.(26) [33].

where k is the coefficient of elastic foundation.

According to the thin plate theory,the internal force of bending moment is as follows [32].

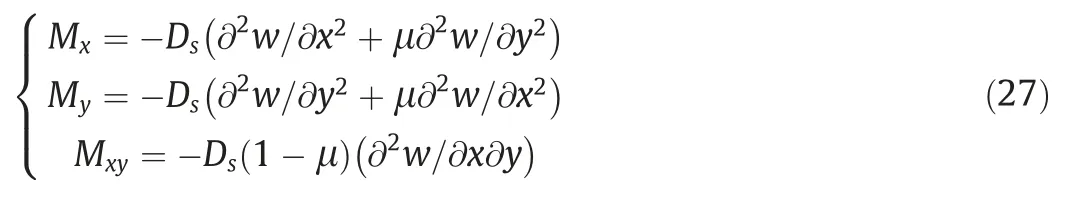
where Mxand Myare the bending moments in MPa;and Mxythe torque in MPa.

When gangue backfilling material is regarded as the elastic material,the deflection equation of thin plate bending is as follows[34].

where m,n=1,2,3,···;and B=π2(2 m -1)2/a2+π2(2n -1)2/b2.

4.5.2.Solving fractional order of thin plate on viscoelastic foundation

Eq.(29) can be obtained by substituting Eq.(26) into Eq.(14).

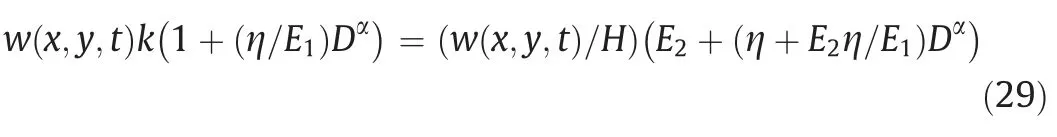
where H is the mining height in m.

Eq.(30) can be obtained by Laplace transform of Eq.(29).

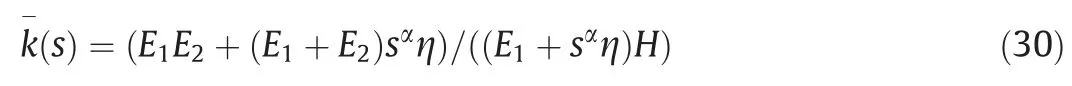
Eq.(31) can be obtained by Laplace transform of Eq.(25).

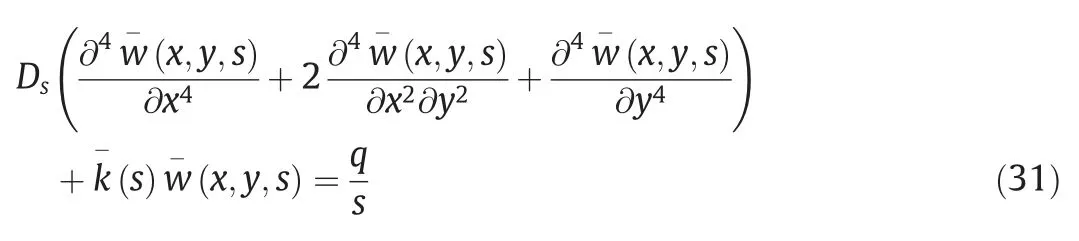
From Eq.(28),when the foundation is elastic,the Laplace expression of the bending deflection of the thin plate is as follows.

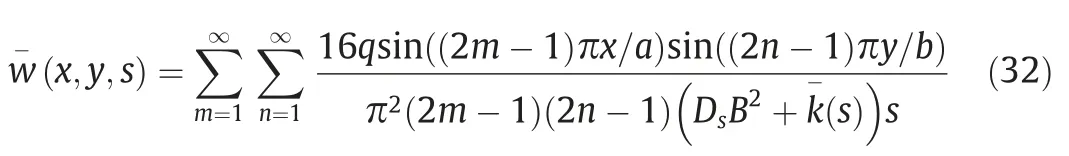
The Laplace deflection equation of thin plate on the viscoelastic foundation can be obtained by substituting Eq.(30)into Eq.(32)as follows.

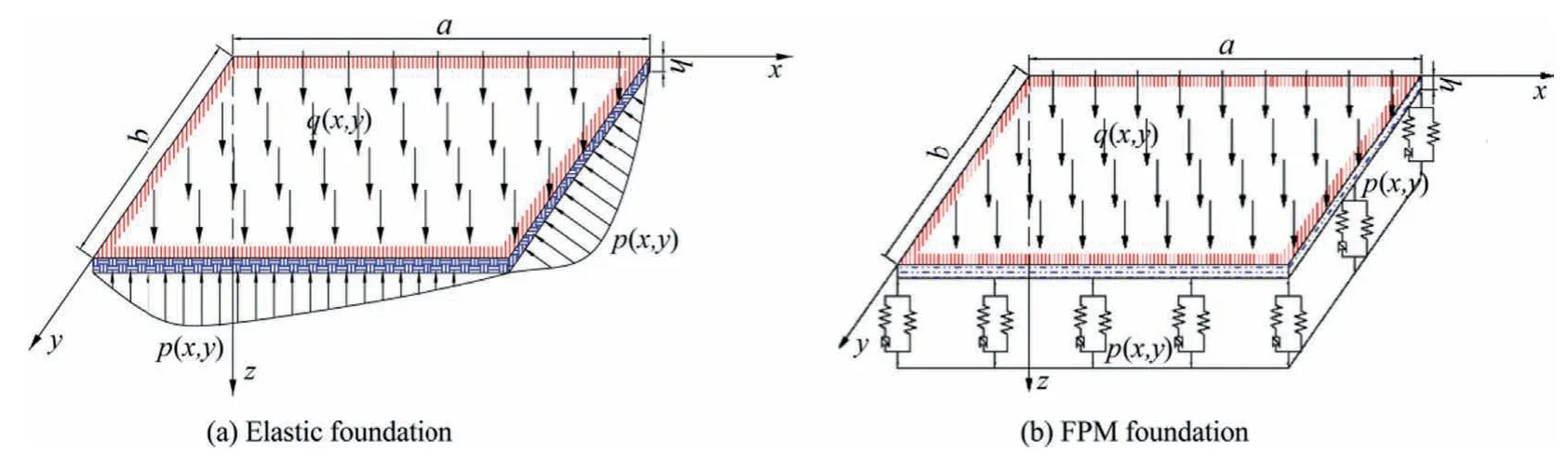
Fig.5.Thin plate on the fractional viscoelastic foundation and elastic foundation.

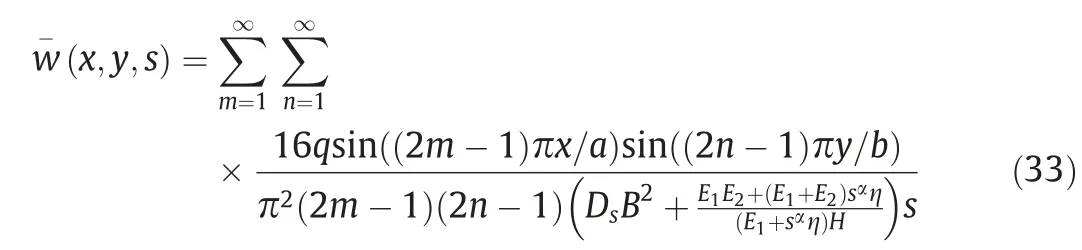
By sorting out Eq.(33),Eq.(34) can be obtained as follow.

Extraction of a common factor after separation of variables from Eq.(34),Eq.(35) can be obtained as follow.

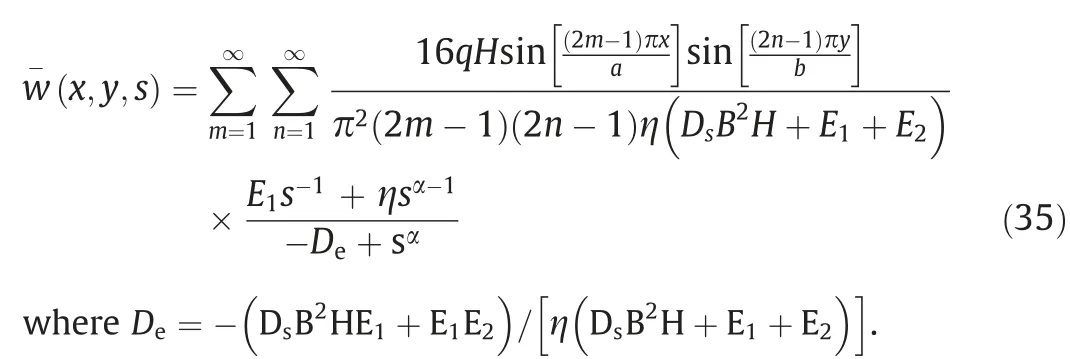
The inverse Laplace transform was applied to Eq.(35) and a double-parameter Mittag-Leffler function was introduced.The deflection equation of thin plate on the viscoelastic foundation was obtained as follows.

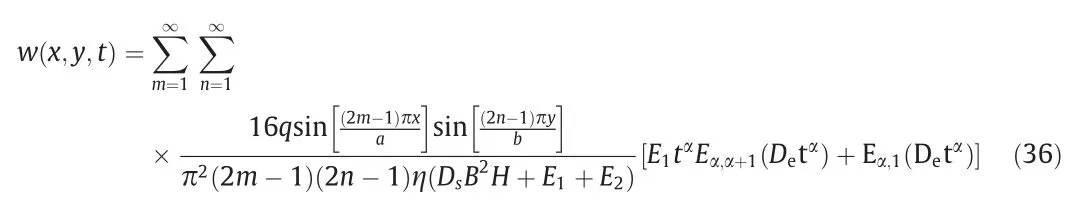
4.5.3.Example calculation

The example coal mine panel has a length of 280 m and a width of 80 m.The average thickness and mining height of the coal seam is 6.8 and 3 m,respectively.The remaining 3.8-m top coal is reserved as the immediate roof.The working face uses gangue backfilling material to backfill the goaf.The roof of the coal seam is limestone with 9.7 m thick;the false roof is locally developed mudstone with a thickness of 0.5 m,and the floor is sandy mudstone.

According to the geological conditions of the panel and the research of Jiang et al.[35],when the advancing distance of the working face is twice the width,the roof fracture height reaches the maximum,the stratum enters the stage of full subsidence,and the roof deformation tends to stabilize.In order to facilitate the calculation,take a=200 m,b=80 m,h=3.8 m,and H=3.0 m.In laboratory tests,the elastic modulus of coal is 5.8 GPa,and the Poisson’s ratio is 0.27.The load q above the roof mainly comes from the weight of potential caving strata,q=1.525 MPa.The creep time of FPM is 2 h.Considering the calculation time and accuracy,the first three terms of infinite series m and n in Eq.(36) and the first ten terms of infinite series k0in double-parameter Mittag-Leffler function are calculated.By substituting the above parameters and creep parameters (Table 2) into Eqs.(26),(27),and(36),the roof surface subsidence and stress distribution of elastic foundation and fractional foundation can be obtained as shown in Fig.6.

Fig.6a and b shows that the roof subsidence forms of elastic foundation and fractional foundation are concave because the four sides are fixed boundary conditions.The displacement of the roof is 0,and the maximum roof subsidence can be observed in the center.When the solid backfilling material was calculated with the elastic foundation element,the maximum roof subsidence is 245.23 mm;and when it is calculated with the FPM,the maximum roof subsidence is 249.16 mm (Fig.7).Compared with the maximum roof subsidence of the elastic foundation,the maximum roof subsidence of the fractional viscoelastic foundation increased by 1.60%.It can be seen that the roof subsidence of the thin plate model on fractional viscoelastic foundation basically coincides with the elastic foundation.

Fig.6c-f show that the roof bending moment forms of elastic foundation and fractional foundation are concave,and the maximum bending moment in x-direction Mxand maximum bending moment in y-direction Myare found in the goaf center.When calculating solid backfilling materials with elastic foundation elements,Mxand Myare 4.65 and 11.27 MPa;when calculated with the FPM,Mxand Myare 5.23 and 13.05 MPa,respectively(as shown in Fig.7).Comparing the maximum bending moment in x-direction Mxand maximum bending memoment in y-direction Myfor both elastic foundation roof and fractional viscoelastic foundation roof,the increments of Mxand Myin the FPM are 12.5% and 15.8%,respectively.

5.Discussion

5.1.Time-dependent properties of roof deflection

SBM is mainly applicable where surface subsidence must be controlled and minimized.Typical applications are therefore when undermining buildings,water bodies,and railways.The threedimensional surface of the deflection of fractional viscoelastic foundation thin plate with the face’s advancing distance and time is shown in Fig.8.

Fig.8 shows that the roof deflection curves of elastic foundation and fractional foundation are parabolic with opening upward.When the elastic foundation element is used to calculate the solid backfilling material,the deflection curve of the roof will not change with time,and the roof subsidence is constant.When the FPM is used to calculate the solid backfilling material,the roof deflection curve at 2 h is close to that of the elastic foundation.With the increase of time,the deflection of the roof increases,and when t=100 day,the deflection reaches 376.42 mm,increased by 50.9%.

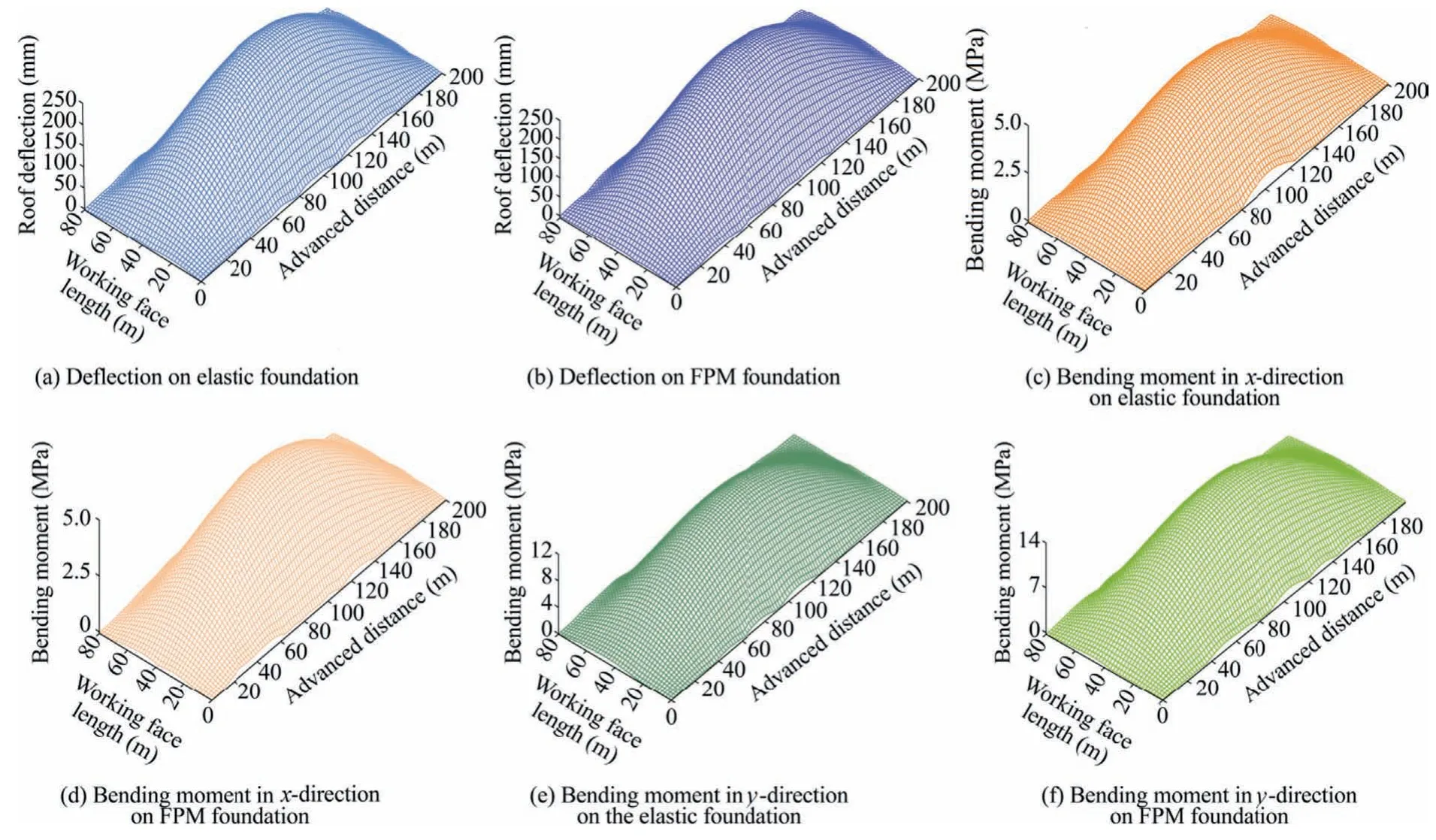
Fig.6.Roof response on elastic foundation and viscoelastic foundation.

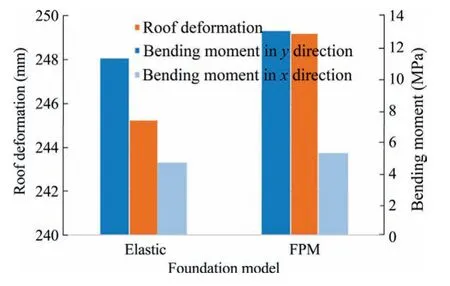
Fig.7.Comparison of elastic foundation and viscoelastic foundation.

During the advancing process of the backfill panel,a monitoring point was laid in the central gob to dynamically monitor the roof convergence.The results of roof dynamic convergence along with panel advancing was shown in Fig.9.

It can be seen from Fig.9 that the initial deformation rate of the roof is relatively high.When the backfilling body is gradually compacted by the overlying strata and the deformation becomes stable,the subsidence of the roof becomes stable.According to the test results,the maximum value of the roof is 366.68 mm,which is consistent with the established model value (376.42 mm).

Similarly,the three-dimensional surface bending moment of fractional viscoelastic foundation thin plate with advancing distance and time of the panel is shown in Fig.10.

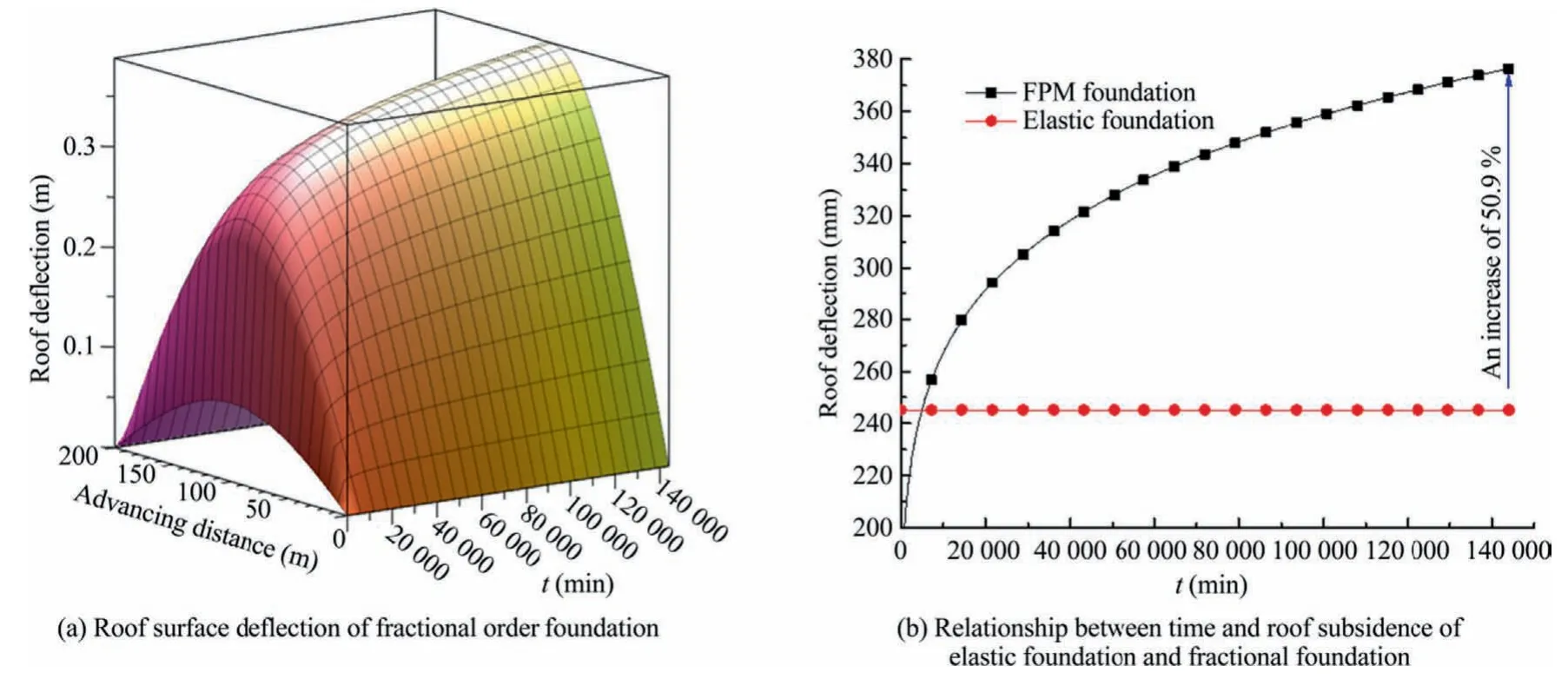
Fig.8.Time-dependent properties of roof surface deflection.

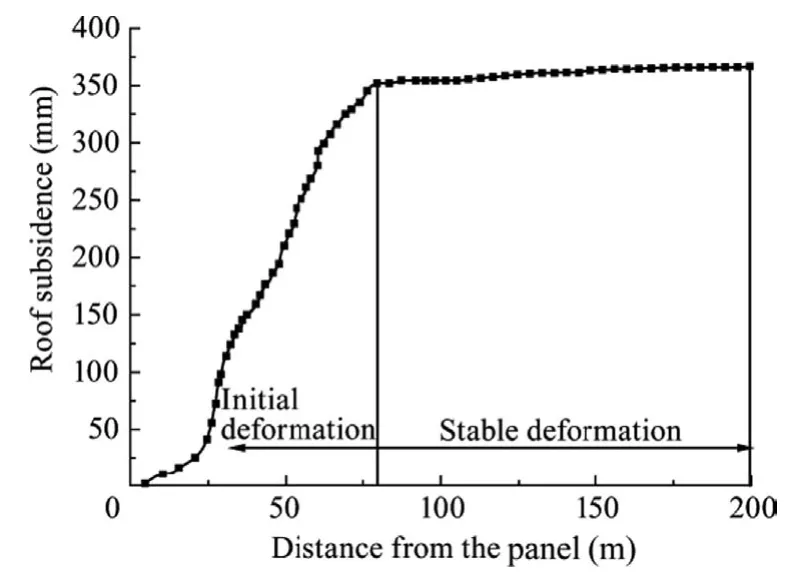
Fig.9.Roof dynamic subsidence monitoring.

Fig.10 shows that when the panel is advancing,the bending moment of the roof with fractional foundation increases first and then decreases,with the maximum bending moment occurring in the center position and gradually increasing with time.When the solid backfilling material is calculated by elastic foundation element,the roof deflection curve will not change with time,and the roof subsidence is constant.When the solid backfilling material is calculated by FPM,the roof bending moment at 2 h is close to that of the elastic foundation.When t=100 day,the bending moment reaches 7.21 MPa,increased by 37.9%.It can be seen that the advantage of the fractional model is that the long-term deformation characteristics and bending moment of working face roof can be predicted by the short-term creep test of gangue in the laboratory.The long-term deformation characteristics of the roof are very important for strata movement and surface deformation and are one of the important indexes for evaluating the effect of solid backfilling mining.

Another important point is that,as the backfilling material is gradually compacted,the deflection and bending moment of roof gradually increase with time.In the field,improving the compactness of backfilling materials can be achieved by increasing the compaction times of backfilling materials,changing the particle size ratio of gangue and increasing other mixtures.

5.2.Viscous properties of fractional viscoelastic foundation thin plates

By changing the compressive properties of materials,when t=2 h,the roof subsidence and Mxof backfilling materials with different viscous coefficients are analyzed.Taking x and y axes as advancing distance of the panel and viscous coefficient of backfilling material respectively,the three-dimensional surface of roof deflection and bending moment Mxin solid backfilling mining are shown in Fig.11.

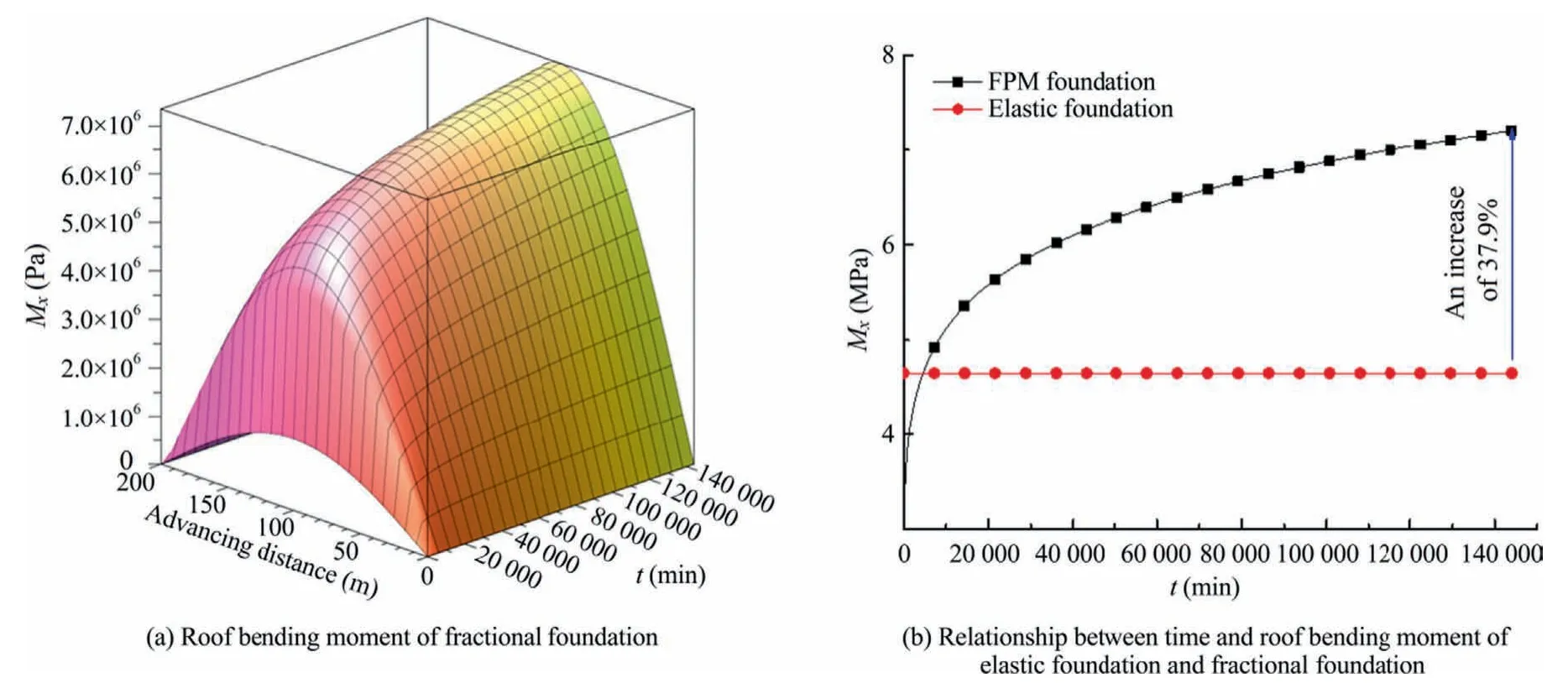
Fig.10.Time-dependent properties of roof bending moment in the x-direction.

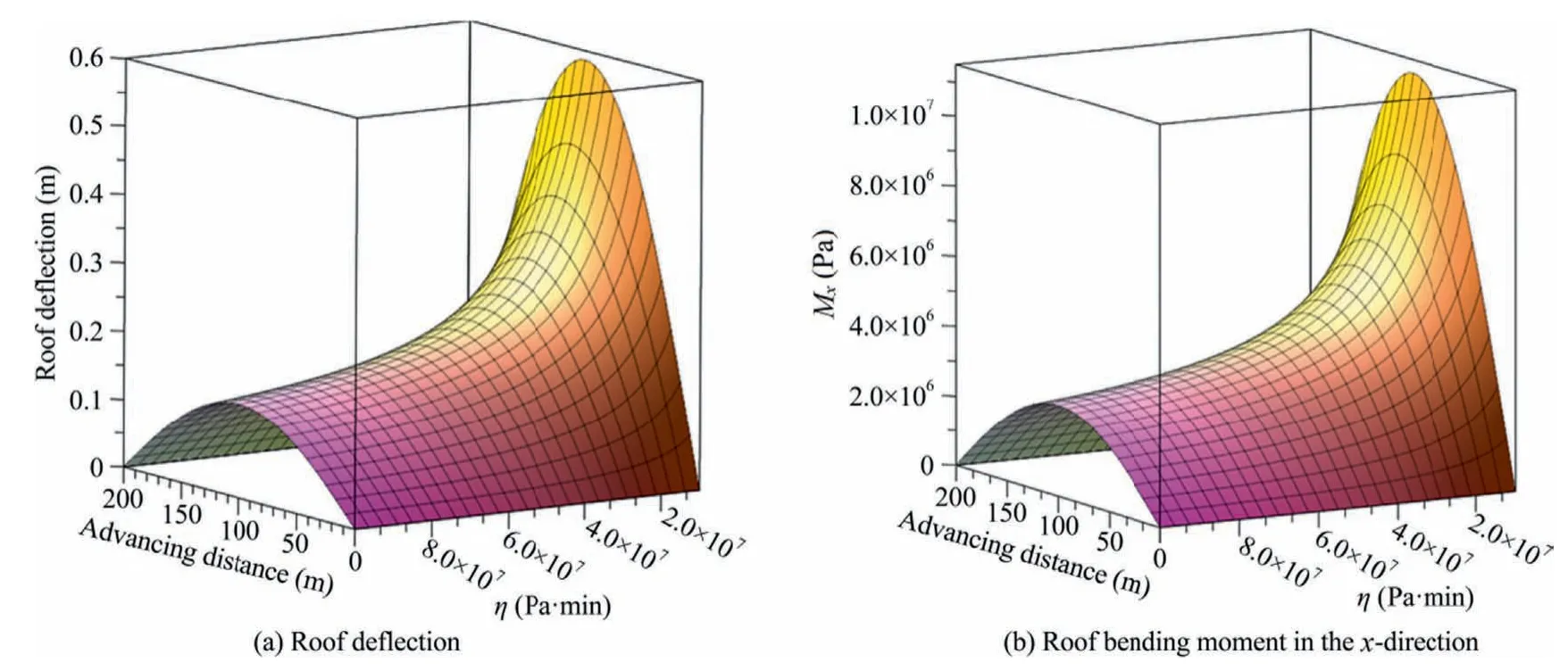
Fig.11.Viscous properties of the three-dimensional surface of roof subsidence and Mx .

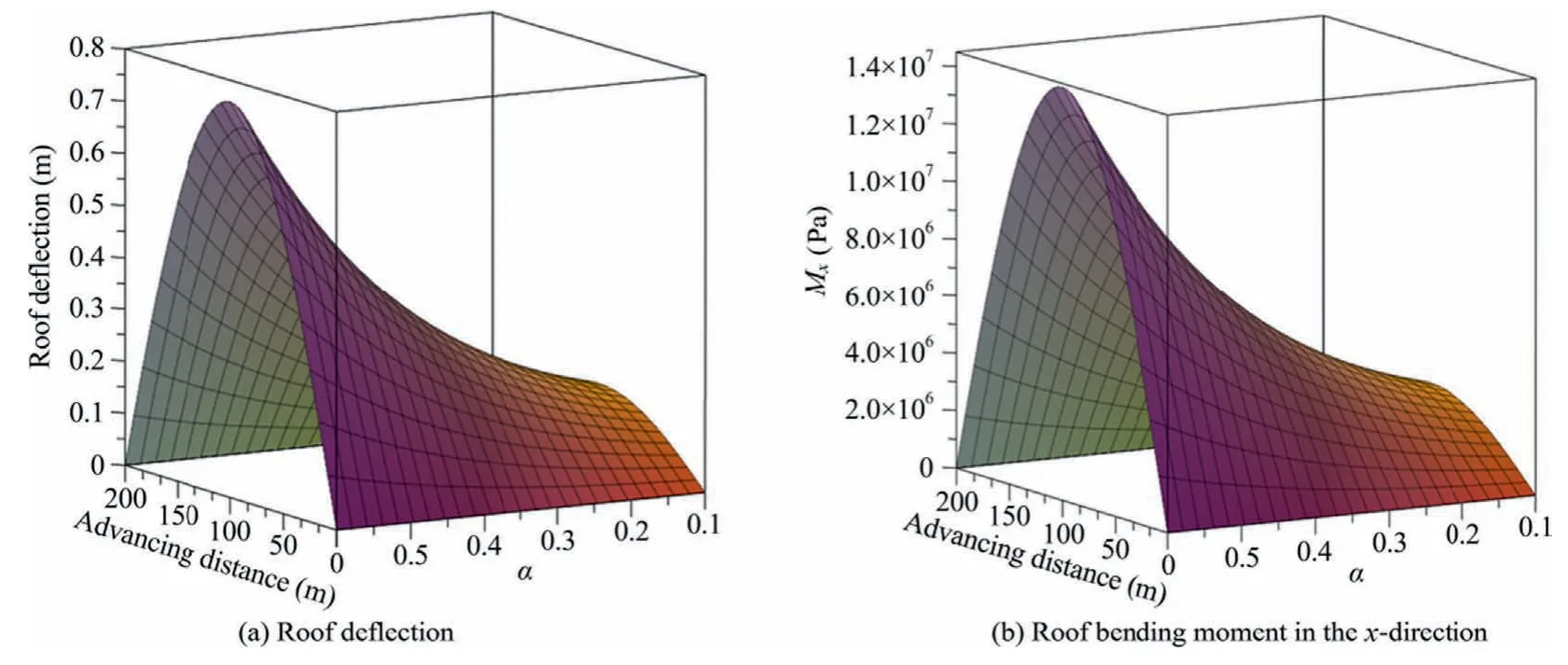
Fig.12.Order properties of the three-dimensional surface of roof subsidence and Mx .

Fig.11 shows that the roof subsidence and the maximum bending moment in x-direction Mxincrease first and then decrease with the advancing distance,while the maximum deformation occurs in the goaf center,showing a symmetrical distribution.The roof subsidence and Mxdecrease rapidly with the increase of the viscous coefficient.When ηα≥50 MPa·min,the values of roof subsidence and Mxare stable basically,which indicates that when the viscosity of solid backfilling material is in a certain range,the effect of controlling roof subsidence is better.

5.3.Order characteristics of fractional viscoelastic foundation thin plates

By analyzing the order of fractional foundation,the deflection and bending moment of the roof in solid backfilling mining under different order and advancing distance are shown in Fig.12.

Fig.12 shows that the roof subsidence and Mxalso increase first and then decrease with the advancing distance,and the deformation in the central position of the goaf reaches the maximum,showing a symmetrical distribution.The roof subsidence and Mxincrease gradually with the order.Compared with the elastic foundation model,the fractional order foundation model can accurately describe the roof subsidence and bending moment by changing the order.Therefore,the fractional foundation model can be fitted by the laboratory data and the accuracy of the model can be improved by changing the order,which solution of the plate on the foundation is also higher precision.

6.Conclusion

Based on fractional calculus theory,this paper establishes the usefulness of the SBM thin plate model with a fractional viscoelastic foundation.The expressions of deflection and bending moment of a thin plate are obtained.The time,viscous and order characteristics of the fractional viscoelastic foundation are discussed.The conclusions are as follows.

(1) The study of gangue backfilling materials in this research was conducted under five groups of lateral confinement compression tests,taking the axial stresses of 2,5,10,15,and 20 MPa,respectively,as test conditions.The compaction characteristics and time-related characteristics of gangue were analyzed in detail.The deformation of gangue can be divided into two stages:deceleration deformation and stable deformation.After 30 min,the deformation rate is basically stable.

(2) The FPM model was established and the parameters of the FPM were identified.Compared with AD,FMM,FKM,and FGKM,the FPM is more consistent with the experimental data and the accuracy is higher,which prove that the FPM is reliable and calibrated to the real mining situation.

(3) The thin plate roof model of SBM based on the fractional viscoelastic foundation was established.The deflection and bending moment equations of the thin plate were derived.The difference between the thin plate model of solid backfilling mining on the fractional viscoelastic foundation and the elastic foundation model was discussed.When t=2 h,the deflection and bending moment values of the two models are basically consistent.

(4) The time characteristics,viscous properties and order characteristics of the roof model with fractional viscoelastic foundation were discussed.When t=100 days,the deflection and bending moment are 388.027 mm and 7.35 MPa,which increased by 65.5% and 58.06%,respectively.When ηα-≥50 MPa·min,the values of roof subsidence and bending moment in x-direction Mxbecome stable,which indicates that when the viscosity of solid backfilling material is within a certain range,the effect of controlling roof subsidence is better.

Acknowledgements

This research was funded by the National Science Fund for Distinguished Young Scholars (No.51725403),the National Natural Science Foundation of China (No.52004271),the China Postdoctoral Science Foundation(Nos.2019M661990and 2018M632410),the Fundamental Research Funds for the Central Universities (No.2020QN05).