An updated empirical model for ground control in U.S.multiseam coal mines

Mine Safety and Health Administration,Pittsburgh,PA 15217,USA

Keywords:Underground Coal Multiseam Ground control Pillar design Empirical

ABSTRACT Multiple seam interactions are a major source of ground instability in several U.S.coalfields.Empirical methods are well suited for this problem,because while the mechanics multiple seam interactions are very complex and poorly understood,many mining case histories are available for analysis.This study makes use of an updated database that includes 356 multiseam case histories,including 67 unsuccessful designs.The paper describes in detail the process used to design the study,collect the data,conduct the statistical analysis,and develop the quantitative model.The model can be used for mine planning in multiple seam situations,and has been made available as a module within the Analysis of Coal Pillar Stability(ACPS) computer program.

1.Introduction

In mature coalfields around the world,today’s mines are often affected by older workings in coal seams above or below the current operations.In the U.S.,the most heavily impacted coalfields are in the Central Appalachian (CAPP) region of southern WV,western VA,and eastern KY(see Fig.1).A 2010 survey of 40 active deep-cover room and pillar mines in the CAPP found that 80% of them were subject to multiple seam interactions[1].In the Northern Appalachia (NAP) coalfields,as many as 50% of the room and pillar mines may be affected,though the impact tends to be reduced because these mines operate under lighter cover[2].Many Western coal mining operations also work in multiple seam configurations,particularly in central UT and western CO[3].Even in the Illinois Basin(ILB),where mines have generally been able to avoid the most severe types of interactions,several operations have recently unexpectedly encountered unusual multiple seam interactions [4].

2.Hazards associated with multiple seam mining

Ground instability is the most common effect of a multiple seam interaction.A severe interaction can result in roof deformation,severe rib sloughing,and/or floor heave (Fig.2).A survey of 36 U.S.multiple seam coal mines conducted in the mid-2000′s identified 77 individual cases of instability that were attributed to interactions [5].In 29 of these cases,development had to stop or panels had to be abandoned because of the difficult conditions that were encountered.Large roof falls occurred in 20 other cases,often resulting in the loss of individual mine headings.Most of the remaining cases involved pillars that were abandoned during retreat mining operations.Pillar squeezes (widespread propagating pillar failures) occurred in at least three cases,and four cases reportedly involved coal bursts.

Since 2010 at least two miners have been killed by rib falls that were triggered by interactions.In a PA operation,miners were developing a set of entries located approximately 25 m above underlying abandoned room and pillar works.High stresses above unextracted remnant pillars in the lower mine,where surrounded by pillar recovery,caused significant roof deterioration in the overlying active mine.When the continuous miner extracted the stressdamaged roof rock with the coal,it created a 0.6 m thick rock rib brow at the top of the excavation.A large slab of this brow rolled off,killing the continuous miner operator[6].A similar incident occurred in eastern KY in 2012.In that case,the active workings were located 13 m above an abandoned underlying mine.As the section advanced over a remnant barrier pillar,the ribs were damaged by the additional stress.The victim was setting timbers for rib control when an 8 m long section of the rib rolled off,killing him [7].

Fig.1.Underground coalfields of the U.S.

Fig.2.A multiple seam interaction.An overlying remnant structure has caused roof failure and rib sloughing in an active seam.

Fortunately,no recent roof fall fatalities have been attributed to multiple seam interactions.Many instances of roof instability have been reported in literature,however.Zhang et al.documented a shallow-cover case from NAP in which the active,overlying seam encountered serious roof cracking near the edges of an area underlain by small pillars that were assumed to have failed[8].Tulu et al.[9,10]and Klemetti et al.[11]showed how multiple seam mining interacted with in situ horizontal stress to damage the roof at a CAPP mine.Two examples of severe interactions resulting from mining above previously extracted longwall and pillar retreat panels are discussed by Grimm et al.[12]and Morsy et al.[13].Zhang et al.documented severe floor heave and rib spalling that developed in bleeder entries located beneath barrier pillars in an extracted seam 20 m above [14].

Multiple seam interactions also contribute significantly to risk of coal bursts [4,15].In the North Fork Valley of CO,for example,10 of the 36 reported bursts have occurred in association with multiple seam mining [16].Multiple seam interactions contributed to two recent fatal coal bursts in the eastern U.S.The 2014 burst that killed two miners during pillar recovery operations in WV was located beneath remnant barrier pillars surrounded by retreat mining in two overlying seams (Fig.3) [17].The previous year a KY burst killed a continuous miner operator and injured two other miners.In that incident,retreat mining had just emerged from beneath the protective‘‘stress shadow”of a worked-out(gob)area[18].Several non-injury coal bursts have also occurred during development advance mining in association with multiple seam interactions [19-22].

Another multiple seam hazard is the potential for inundation from an overlying,flooded mine [23,24].A review of MSHA data indicates that of the 166 inundation incidents that were reported between 2000 and 2015,five resulted when caving associated with full extraction in a lower seam intersected water-filled overlying workings.No injuries were associated with any of these incidents.The investigation of the Upper Big Branch mine disaster disclosed that an unreported inundation occurred some months prior to the explosion.Longwall panel extraction in the active lower seam caused water impounded in an overlying abandoned mine to flood the headgate entries,restricting ventilation flow until it was pumped out [25].

Fig.3.Coal burst in a multiple seam pillar recovery operation in WV.The two overlying seams (marked in blue and orange) had already been extracted.Pillar recovery in the lowest seam (marked in black) concentrated the load on the two pillars that burst (marked in red).

Interestingly,development above gob areas has been frequently associated with large,but temporary,groundwater inflows [26-29].In these cases,the fractures in the subsided overburden above the abandoned mine become filled with groundwater.The groundwater later drains into the overlying mine when its development intercepts the water filled fractures.Fractures in subsided zones can also fill with methane or oxygen-deficient air,resulting in inflows of methane or blackdamp as apparently occurred in one UT longwall [30].

Since 2007,mine planners and regulators in the U.S.have used the Analysis of Multiple Seam Stability(AMSS)to evaluate the hazards associated with potential multiseam interactions [5,31,32].The current study builds upon AMSS,and on the original case history database that was employed in its development[33].The multiple seam model developed from this study was incorporated into the recently developed ACPS pillar design program.

3.Empirical methods in mining ground control

Multiple seam mining is an excellent candidate for an empirical method.The value of numerical modeling for multiple seam analysis is limited,because multiseam mechanics are extremely complex and poorly understood,and because all the necessary rock mass material properties are unlikely to be available for the inherently complicated mining scenarios.Empirical methods,on the other hand,can make use of the wealth of real world mining experience that can be collected.Every pillar that is mined,entry that is developed,or multiple seam interaction that occurs represents a full-scale test of a rock engineering design.By harvesting such data,and then using the appropriate statistical techniques to interpret them,mining engineers have developed powerful design techniques that are widely used around the world for many applications.Successful empirical methods are readily accepted because they are simple,transparent,practical,and firmly tethered to reality [34].

The empirical approach requires that the researcher begins with a clear hypothesis,in the form of a simplified model of the real world that abstracts and isolates the factors that are deemed to be important to the problem at hand [35].The conceptual model must be based on a thorough understanding of the fundamental mechanics,and it in turn guides the data collection,the statistical analysis,and ultimately the final product.

Mark[34]described a six-stage process for the development of a successful empirical design method.These stages are:(1)identification of the problem,and of the end users of the final product,(2) development of a conceptual rock mechanics model,and identification of the key parameters in that model,(3) identification of measures for each of the key parameters,and the development of new measures where necessary,(4) data sources,data collection,and development of a case history data base,(5)statistical analysis,and selection of the appropriate statistical methods,and (6) packaging the final product for the end users.

The next sections of this paper will discuss how this approach was used to develop an empirical technique for multiple seam mine design.

4.Problem identification

As discussed above,multiple seam interactions can affect safety in a number of ways.The focus for this project was on roof,rib,and pillar instability,because of the abundance of available case history data.Inundations were not addressed because their mechanics are quite different.Coal bursts were initially included,but since multiple seam interactions are only one factor contributing to the complex mechanics of a burst occurrence,ultimately they were excluded as well [36].

Some older design methods proposed for multiple seam mining have not been clear about whether they are applied to the whole mine,or just some specific locations[3].Such schemes are of little use to mine planners,who face the challenge of determining which remnant structures may cause interactions,and then what to do about them.Possible interventions include design changes such as larger pillars,more roof or rib support,or a new layout that avoids the structure entirely.Mine planners must make these decisions on a case-by-case basis,since the nature of the potential interactions can vary substantially from location to location even within a single mine.

The goal of this project was therefore to develop a design methodology that could evaluate the risk associated with each individual multiple seam interaction,and to suggest appropriate control strategies.However,it was also critical to clearly identify the failure modes that are being addressed.This requires a thorough understanding of the mechanics of multiple seam mining.

5.Conceptual model:The mechanics of multiple seam interactions

Multiple seam interactions come in many guises,and historically have caused significant confusion among researchers.For example,one study found that ‘‘stresses from superincumbent workings are not transferred through shale strata for distances of over 33 m”[37],while another observed that‘‘a stress transfer distance of 225 m has been recorded between longwalls”[38].Mark showed that there are four distinct types of multiple seam interactions,each with its own characteristics and effects [3].Significant new findings during the past decade have further refined the understanding of the mechanics of multiple seam mining.

5.1.Undermining

Undermining is the most common type of interaction.It occurs when the upper seam has been mined first and the lower seam is the active seam (Fig.4).In an undermining situation,highly stressed remnant structures in an overlying mine can cause vertical stress concentrations in the underlying seam.Remnant structures are typically created when unmined coal is left adjacent to worked-out (gob) areas where the coal has been fully extracted.

Fig.4.Undermining.

Many different types of remnant structures can be encountered,including barrier pillars,longwall chain pillars,un-extracted or partially-extracted production pillars,unmined coal,or even sandstone washouts.A UK National Coal Board study found one case where an isolated remnant pillar (in this instance a remnant surrounded on all sides by gob) caused a disturbance 135 m below,while nearby a boundary between a gob area and solid coal had no noticeable effect just 27 m below.Clearly the isolated remnant pillar resulted in a significantly greater stress concentration in the underlying seam than the gob-solid boundary.The study concluded that it is ‘‘extremely dangerous to dismiss interaction effects purely on the basis of the thickness of the interval between the seams”[39].

During the past 10 years there has been an increasing recognition of the role of ‘‘pseudo-gobs”in creating remnant structures[4].Pseudo-gobs occur when areas containing smaller,unmined pillars‘‘behave”like a gob by transferring load to a larger,adjacent pillar.This phenomenon is most likely to occur when the small pillars have failed or punched into the floor,but there have been several instances where the small pillars were likely intact yet still transferred load to the larger pillar.It appears that whenever there is a significant ‘‘stiffness contrast”between the small pillars and the large one,a pseudo-gob effect may develop.Pseudo-gob interactions have been associated with rib instability in western KY and WV,roof failure in PA and eastern KY,and coal bursts in eastern KY and southern WV [4,40].

The type of interburden geology can play an important role in determining the extent of load transfer.Haycocks et al.used photoelastic modeling to show that a softer interburden,either due to a large number of rock layers or a low modulus of the individual layers,results in an elongated pressure bulb that reaches deeper seams below [37].Strong and massive interburden,on the other hand,would be expected to distribute the load more widely.Also,the immediate roof geology and the compatibility of the installed support with the geology and stress interaction are essential factors for entry stability.The same multiple seam stress transfer that causes great damage to weak roof,requiring heavy supplemental support,might not even be evident where the roof is strong.

Theory also suggests that the angle of approach to remnant structure could be significant.Retreat mining beneath (or above)solid coal that proceeds towards a worked-out gob area would be expected to create a highly stressed‘‘window”(Fig.5)that the vertical load passes through [41].

A recent study demonstrated that steep topography can effect multiple seam interaction.At this KY mine,panels are developed in the‘‘stress shadow”beneath previously extracted overlying panels.In one instance,however,the outside entry of one panel was unexpectedly subjected to large deformations.Underground mapping combined with two-dimensional FLAC modeling showed that the principle stresses were inclined from the vertical due to the influence of the mountainside which offset the location of the stress shadow.When the outside entry was relocated a further 10 m beneath the gob away from the ridge,conditions improved dramatically [9].

Fig.5.Effect of retreat mining direction when approaching a gob-solid boundary(after [41]).

5.2.Overmining

The second type of interaction,overmining,occurs when the upper seam is extracted after mining is complete in the lower seam(Fig.6).Load transfer occurs during overmining just as it does with undermining,because remnant pillar structures will cause stress concentrations both above and below.In addition,however,overmining conditions may be affected by subsidence resulting from full extraction of the underlying seam.

Fig.7 is a conceptual model that illustrates the type of damage that can be expected within the overburden due to subsidence above a full extraction panel.Five broad zones of overburden behavior can be identified [42-44],with the degree of damage decreasing as the distance to the extracted seam increases.Any overlying coalbed located within a height of approximately 6-10 times the lower seam thickness is likely to be entirely caved and difficult to mine.Coalbeds located between 10 and 30-60 times the lower seam height are likely to be largely continuous,but their roof strata may be fractured or otherwise damaged.Open cracks can be encountered in the subsidence tensile zones which are normally located over the gob,10-30 m laterally from the underlying edge of the remnant structure.The roof in these zones may also lack horizontal confinement,creating conditions where large roof falls may occur with little warning.The subsided ground may also have been fractured and damaged by the subsidence process,even if it is not currently within a tensile zone.

Fig.6.Overmining.

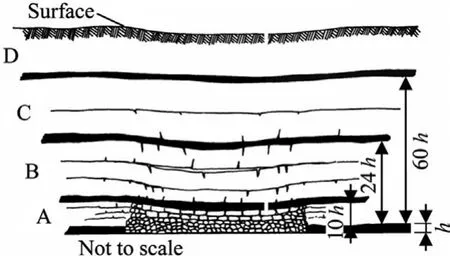
Fig.7.Five zones of overburden behavior in response to full-extraction mining(after [43,44]).

Early studies of multiple seam interactions generally concluded that overmining could be successful with interburden distances of 6 m or even less[45-47].It seems that these studies described conditions over extensive,fully extracted gob areas,however,and did not address the effects of isolated remnant structures left within the gob.In contrast,Stemple observed that some evidence of subsidence-induced damage could be observed in nearly every overmining case he examined [48].In one recent case history,Zhang et al.observed significant roof cracking in a tensile zone above an area of failed pillars,even though the depth of cover was only 60 m and there was 36 m of interburden [8].

5.3.Dynamic interactions

In the overmining and undermining interactions described thus far the previous mining is complete before the active mining begins.Dynamic interactions can occur whenever active mining is conducted above or beneath previously developed workings in a mine that is still operating.The most severe dynamic interactions occur when a lower seam is longwalled or pillared beneath overlying entries,causing the open overlying workings to subside.At least three modern cases have been reported in literature,and the overlying entries were lost or severely damaged in every case even though the interburden was as great at 150 m[3,49,50].Less intense dynamic interactions can also be associated with full extraction in an overlying seam,or even,in extreme cases,by development mining above or below.

Because dynamic interactions are generally far more severe than static ones,experts have been warning for nearly a century that retreat mining should never be conducted beneath active workings [28,45,48,51].

Less predictable are instances in which delayed subsidence of underlying works has the same destructive effect on overlying entries.Delayed subsidence refers to a situation where the mining has been completed in the lower seam,but because the extracted panel is relatively narrow,the subsidence takes some time to work its way upward.If mine workings have been developed in an overlying coal seam during the interim,they will subside and underlying subsidence as a dynamic interaction will occur.

Mark and Barker described another type of dynamic interaction whose effects can be so severe that the entire mine is abandoned[52].In this instance,the active mine had been developed over an extensive area of intact pillars.When retreat mining commenced in the upper seam,however,the abutment load was transferred to the underlying pillars,triggering a squeeze.The failure of the underlying pillars was experienced in the overlying mine as a dynamic multiple seam interaction that caused widespread extreme roof and rib deformation and destroyed numerous ventilation controls.

5.4.Ultra-close mining

The ultra-close type of interaction is the one in which the stress redistribution resulting from development mining alone is significant,that is,an ultra-close interaction can occur without full extraction or a pseudo-gob.Ultra-close scenarios are most likely to occur near where a thick seam splits and mining is conducted both above and beneath the rock parting,or where a rider coalbed is of mineable thickness.

The primary concern is failure of the interburden between the two seams,and a key factor is the relative vertical positioning of the pillars in the two seams[53].The beam of interburden can fail either through shear caused by pillar punching,or by tension caused by the self-weight of the rock plus that of any machinery working on the interburden beam (Fig.8).

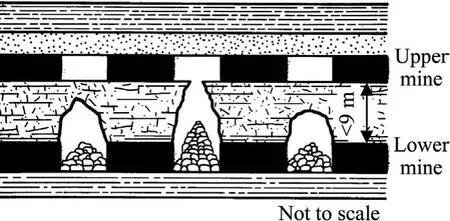
Fig.8.Ultra-close mining (after [41]).

Ultra-close interactions are unlikely when the two seams are more than 6-10 m apart,unless the interburden is unusually weak or the depth of cover unusually great [53,54].Zhou and Haycocks determined that the minimum safe working thickness for a massive,unstratified sandstone was just 3 m,while for shale it was 6 m [55].Columnization of the pillars is considered the standard design practice when ultra-close interactions are a concern[54,56].Ultra-close mining is commonly encountered by multiple seam highwall mining operations [57].

5.5.The multiple seam model

Of the four mechanisms discussed above,many case histories of undermining and overmining are available.The mechanics of these two interactions also have much in common,the primary difference being that subsidence effects are not present in undermining.On the other hand,ultra-close and dynamic interactions are very unusual in the U.S.,and their mechanics are also very different from the other two types of interaction.The proposed model therefore focused exclusively on undermining and overmining.

As the preceding discussion has shown,the mining conditions associated with any particular multiple seam interaction are the product of a highly complex and interrelated set of parameters.The geologic and mining factors that could be incorporated into a model are shown in Table 1.

It is essential that no important parameter be left out of the data simply because it is hard to obtain or measure.This leads to the next step in the modeling process.

6.Parameter development

The measurement of many of the parameters listed in Table 1 is relatively straightforward.Some parameters are categorical,for example the‘‘type of mining”can be either ‘‘development”or‘‘retreat”.Others,like the depth of cover,are readily determined from maps displaying overburden contours.Pillar dimensions and interburden thicknesses are available on mine maps and core logs,and the ratios of overburden-to-interburden and interburden-to-under lying-seam-thickness can be calculated.

Rating scales make it possible to include other critical variables that are difficult to measure directly.Rock mass classifications,such as the coal mine roof rating (CMRR),are the best-known examples of rating scales used in empirical techniques.Rating scales take advantage of the fact that empirical modeling essentially involves comparing case histories to one another,so it only requires accuracy in a relative sense,not an absolute one [34].A successful rating scale must also be simple enough that future users of the design method will be able to understand it and to collect the necessary data.

‘‘Type of remnant structure”was a key candidate for a new rating scale.A complicated rating scale that tried to separate the varieties of remnants into too many classes might have proved unworkable,and might not have improved the reliability of the model in any case.Ultimately,the remnant pillar variable was designed with just two levels:(1) gob-solid boundary,or (2) isolated remnant pillar.A gob-solid boundary can distribute its load over a larger area,so its stress levels are lower and its effects are less noticeable.An isolated remnant,on the other hand,is subjected to at least two overlapping abutment loads,so the impact of the resulting stress concentration on the underlying or overlying active seams is significantly greater (Fig.9).

Three geologic rating scales were used in this study.The CMRR was used to rate the competence of the immediate roof in the active seam [58].The percentage of competent rock in the interburden was calculated at each borehole by summing the total thickness of sandstone,sandy shale,and limestone,and then dividing by the total interburden thickness.The number of beds in the interburden was also estimated from the core logs.

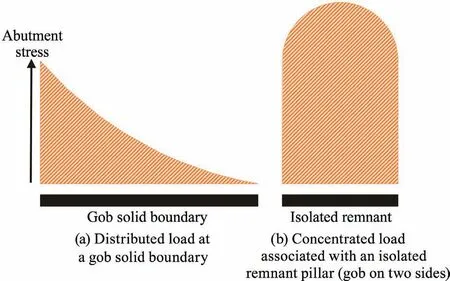
Fig.9.Load distributions associated with two types of remnant structures.

Table 1 Geologic and mining factors affecting multiple seam interactions.

Originally,the plan was to use the NIOSH Analysis of Roof Bolt Stability (ARBS) method to measure the amount of support installed [59,65].However,it was found that in almost every instance the primary support consisted of 1.2 or 1.5 m fullygrouted resin bolts.With so little variation,it did not make sense to include primary support as an independent variable.Supplemental support was installed in some cases,but not in others.The amount of supplemental support did not vary much,and where it was installed almost always consisted of a pattern of 2.4 to 3.6 m long cable bolts or resin-assisted mechanical bolts.Therefore,extra supplemental support was included as a ‘‘yes/no”variable.

Estimating the multiple seam stress for each case histories presented a significant challenge.Because of the large number of case histories,this study employed the two-dimensional Lam2D version of LaModel [60].Some simplifications were necessary in order to create consistent 2D grids to represent each of the case histories:

(1) Gob widths in the previously mined seam were defined by the least dimension of the gob (in plan view).

(2) Coal elements in the previous seam are modeled as yielding to more accurately simulate the load distribution prior to mining the second seam.

(3) Coal elements in the active seam were modeled as elastic(non-yielding) to better estimate the loads that the ground initially applied to the critical pillars.

(4) An out of plane extraction ratio multiplier was applied to the active seam to account for the crosscuts that could not be modeled in 2D.

Otherwise the standard Lam2D defaults for the rock and coal moduli,lamination thickness,gob stiffness,and yielding properties of the previously mined seam were employed.The key stress output from Lam2D was the average multiple seam stress(MSS)on the critical (most highly stressed) pillar.

The results from the Lam2D analyses were then used to determine the total vertical stress (TVS) and the multiple seam pillar system stability factor for the active seam (SFMS),using Eq.(1):

where SFSSis the single seam pillar system stability factor,calculated using ACPS [33];SSS the single seam stress,calculated by dividing the ACPS single seam load by the load-bearing area of the pillar system;and TVS=SSS+MSS.

The calculated multiple seam SF values were also compared with ACPS recommended SF values [33].

The single most important parameter in the statistical analysis is the outcome of each case history.It is essential that the outcomes be clearly defined,to ensure that all the case histories are properly categorized.Every success must clearly have been successful,and every failure the result of the mechanism(s) being modeled and not something else.Miscategorizing even a few successes as failures,or vice versa,can entirely confuse the statistical trends in the data[34].Relying entirely on the subjective opinions of different observers is not appropriate,because a‘‘success”at one mine might be considered a ‘‘failure”at another depending on the past experience and safety culture at each operation.This study used a combination of reported conditions and evidence from the mine map to rate the outcome:

(1) Successful cases were those where undermining or overmining had occurred,but no effect was reported in the seam actively being mined.Successful cases also included those where the presence of past mining was noticed underground(for example,there was slightly more rib spall or an occasional roof crack),but the interaction was so minor that it did not have any effect on mining operations.

(2) Unsuccessful cases(failures)were those where mining operations were abandoned,or in which mining was completed with significant difficulties as shown by evidence on the mine map (roof falls,entry segments or crosscuts that were not developed,or pillars that were left unmined during retreat operations.)

Some cases were considered‘‘borderline”and were not used in the statistical analysis.For example,where a roof fall occurred above or beneath a remnant structure,but the map showed that nearby non-interaction areas encountered a similar density of roof falls,the case would be considered neither a failure nor a success.

7.Data collection

The largest data base of multiple seam case histories ever collected was the key to the success of the study.Mark et al.described the process that was employed in the original data collection effort[5].First,discussions with mining company personnel and MSHA Roof Control Specialists identified those mines that had experienced the most difficulties with multiple seam interactions.A total of 44 mines were originally identified and visited between 2003 and 2006,nearly all located in the Central Appalachian and Western coalfields.Three mines from the Northern Appalachians were added when the data base was updated in 2017.

At each mine care was taken to collect successful case histories as well as unsuccessful ones.Overlay mine maps,showing both the active mine and past workings above and/or below,were reviewed with experienced mine officials who had first-hand experience of the conditions encountered.Every instance where the active mine had crossed a gob-solid boundary or a remnant pillar was discussed.The officials also provided their best recollection of the support used and other relevant information.These discussions resulted in a preliminary list of case histories for the operation.In general,only those case histories where problems might reasonably have been expected were documented.The study ignored the many cases where the seams were clearly too far apart for interaction to occur.

Underground investigations were also conducted at nearly every mine.It was seldom possible to access more than a few of the historic interaction sites,because many were in sealed or otherwise inaccessible areas.However,underground observations provided a sample of the ground conditions associated with interactions at that mine.Mapping of the conditions was conducted only in rare instances.The underground visits also provided raw data on roof geology and strength for determination of CMRR.The mine officials were also asked to provide AutoCAD files with mine maps for all the seams on the property,together with exploratory drill logs.

The original data base included 344 case histories from 36 different coal mines.The updated database added 53 cases from the three new NAP mines that helped fill several gaps in the original database:

(1) While all original case histories were from the Central Appalachian and Western coalfields,the new ones are all from Northern Appalachia.

(2) The lowest CMRR in the original database was 45,while 16 of the new cases had a CMRR of 40.

(3) The new data includes a number of overmining cases where the depth of cover was less than 150 m.

Two of the new mines were described by Castner [2],and the third was described by Grimm et al.[12].

Another change was that longwall tailgate cases were removed from the data base because they were considered too few to justify a separate class of multiple seam evaluations.Several coal burstcases were also removed from the database.The final database includes 289 successful cases and 67 unsuccessful cases.

Table 2 Characteristics of the 356 case histories in the multiple seam database.

Table 2 shows that about three-quarters of the cases involved undermining,and that 87% of these were successful.In contrast,only 65% of the overmining cases were successes.Retreat mining was attempted in about 20% of cases,and was successful about 70% of the time.The database includes about twice as many gobsolid boundary cases as isolated remnants.The gob-solid boundaries were judged successful 86%of the time,while the success rate for the isolated remnants was 72%.

Fig.10 shows the depth of cover and interburden thickness.For most of the cases,the depth of cover is between 100 and 400 m,and the interburden is less than 70 m.As expected,unsuccessful cases are more prevalent when the interburden is thin.

8.Statistical analysis

Statistics are the tools that science has developed to deal with uncertainty and probability.In other fields,where extremely large databases are available,statistical methods are highly developed.In ground control,with smaller data sets,statistical analysis can only assist engineering judgment;it cannot substitute for it.

The most common multivariate technique is multiple regression,which takes the form

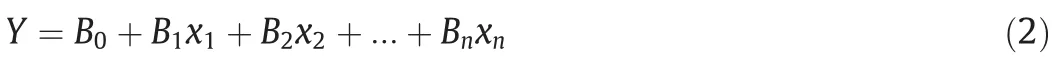
where Y is the predicted value of the outcome variable;x the value of an explanatory variable;and B a coefficient (slope) that is estimated by the regression analysis.The method of least squares is used to estimate the values of the coefficients.

Traditional multiple regression requires that the outcome variable be linear and continuous (like ‘‘stability factor”or ‘‘stress”).When the outcome variable is binary (i.e.there are two possible outcomes,like‘‘successful”or‘‘unsuccessful”as in this study),then logistic regression is the appropriate multivariate statistical technique.

Logistic regression has much in common with linear regression.In both cases,the goal is to predict the outcome as a linear combination of the predictive variables.But in place of solving for Y,logistic regression solves for the likelihood (Z) of a particular case having one of the two possible outcomes.

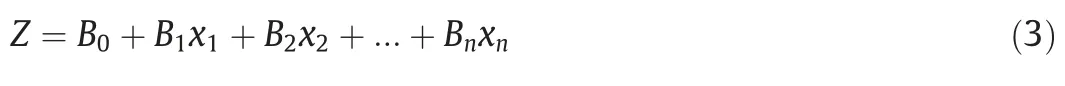
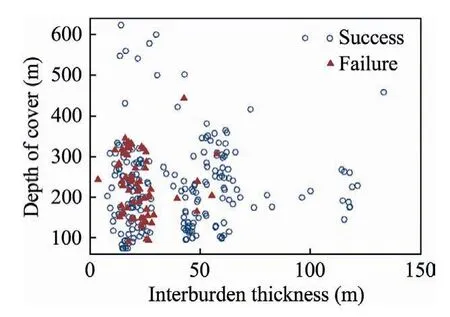
Fig.10.Plot showing overburden depth versus the interburden thickness for the case histories.

where B is a coefficient(multiplier);and x the value of a parameter in the model.The more positive a value of Z is for an individual case,the greater is the likelihood of a positive (successful) outcome,and the more negative,the greater the likelihood of a negative (unsuccessful) outcome.When Z=0,the probability of either success or failure equals 50%.The method of maximum likelihood is used to estimate the values of the coefficients.The statistical package STATA was employed in this study [61].

8.1.Building the model

The process of model-building with logistic regression is also similar to that with linear regression.In general,the goal is to obtain the model that best explains the data with the fewest variables.Logistic regression software provides standard deviations and significance levels for each individual coefficient,which allows their contribution to the overall outcome to be assessed.Variables with little significance can be eliminated from the model.

It is important that any continuous variables used in the model have a linear effect on the outcome.However,this is not a serious restriction,because it is possible to ‘‘transform”a variable so that its effect is linear.For instance,a 10-point decrease in the CMRR from 40 to 30 has a much greater effect on entry stability than a 10-point decrease from 80 to 70.For this reason,the CMRR values in the multiple seam data set were transformed to a new variable called ‘‘lnCMRR20”using the following formula.

Various other transformations of different variables were tested during the model building process,but none resulted in significant improvements.

Another step in the analysis was to weight the cases.Weighting was necessary because some mines provided a large number of case histories,while others provided only a few.To fairly represent all these cases,without allowing the data base to be overwhelmed by a few mines that contributed many cases,the following weighting equation was used.

where Nmis the total number of cases from this mine.This weighting means that the more cases there were from an individual mine,the smaller the weight of each individual case,but the greater the weight of the mine’s total experience.To accommodate the noninteger weights that result from Eq.(5),the‘‘iweight”(‘‘importance weight”) function in STATA was employed.

In the model development,a key issue was whether the undermining cases,overmining cases,development cases,and retreat cases should be analyzed separately or together.There are good scientific arguments for separating them,since the mechanics of the interactions may be different in the different groups.The disadvantage is that the four data bases would each be much smaller.Preliminary analyses showed that all four groups could be combined and analyzed together [5].

Preliminary analysis of the data also indicated that three unsuccessful cases stood out as occurring with much greater interburden depths than otherwise similar cases.Some unique mechanism may have been involved in these cases,or they may simply have been misclassified.Diagnostic tools available within STATA also indicated that these ‘‘outliers”had an inordinate effect on the regression equations.Rather than let them mask the stronger general trends in the data they were therefore excluded.

Correlations between variables within the database are also important to the model building process.In general,when two variables are highly correlated with one another,both cannot be used in the model.For example,in the multiple seam data set,the depth of cover,the single seam stress,and the multiple seam stress were all highly correlated with the total vertical stress.Various combinations of these variables were used in preliminary modeling,before settling on the total vertical stress in the final model [5].The effect of the pressure arch was also tested,and the best results were achieved when the total vertical stress was adjusted by the pressure arch factor [62].

Table 3 shows the correlations between the key variables in the database.Overall,the correlations are not high enough to cause concern,but they do indicate that the data is biased (i.e.nonrandom) in some ways.The most significant correlations occur with the CMRR and Extra Support.Lower CMRR values occur more frequently in association with undermining and gob-solid boundaries,so the model may not accurately reflect the effect of the CMRR in all situations.Similarly,Extra Support occurs in association with more difficult conditions,including weak roof,thinner interburden,and isolated remnant pillars,indicating that it is often installed pro-actively where the conditions are known or expected to be poor.Since Extra Support is preferentially installed where failure is inherently more likely,the final model may not accurately estimate its beneficial effects.

The original analysis found that the pillar SFMSwas a strong predictor of multiple seam stability [5].While it was still significant,the association was less strong in the new expanded data set.Fig.11 shows the multiple seam pillar stability factor plotted against the depth of cover.Of the failed cases,about 30% had an SFMSthat was below the ACPS recommended value of SF=1.5.These included nearly one-half of the retreat cases.In contrast,more than 87%of the successful cases(including two-thirds of the retreat successes) had ACPS SFMSthat exceeded the recommended values.It appears that many multiple seam interactions could be avoided by adjusting the pillar design to account for the additional multiple seam stresses.On the other hand,two-thirds of the cases whose multiple seam pillar SFMSdid not meet the ACPS criteria were successful,and 70% of the unsuccessful cases in the data base cannot be explained by improper pillar design.

The final,best model is given below.

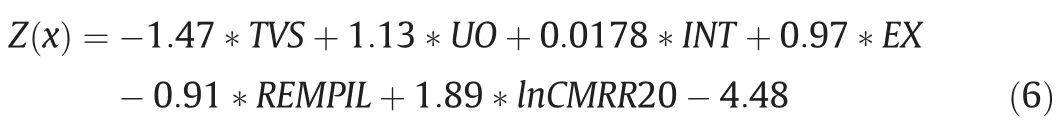
where TVS is the total vertical stress on the critical pillar in MPa;INT the interburden in m;UO=1 for undermining and 0 for overmining;EX=1 for extra support and 0 for none;and REMPIL=1 for isolated remnant pillar and 0 for gob-solid boundary.

Fig.11.Plot showing calculated ACPS multiple seam pillar stability factors versus the overburden depth for the case histories.

All of the parameters in this model are statistically significant at levels above the 98% confidence level (see Table 4).The ROC (a logistic regression analog to the r-squared used to measure goodness-of-fit in multiple regression [63]) is 0.89 for this model.The pseudo r-squared,another goodness-of-fit measure for logistic regression,is 0.32.

For use in mine design,the‘‘probability cutoff”value separating predicted successes from failures was adjusted to from 0.5 to 0.83.This is done by adjusting the constant in Eq.(6) from -4.48 to -6.06.Table 5 and Fig.12 indicate that with this cutoff,the model correctly classifies approximately 76% of the cases overall((216+56)/356),including 84% of the failures.The probability cut-off was adjusted in order optimize the design method by reducing the likelihood of failure to an acceptable level without being unnecessarily restrictive.

8.2.Variables not included in the multiple seam model

The final model does not include a number of variables that past studies had identified as being important to multiple seam analysis.This does not mean that these variables are not important,only that their influence was not identified in this study.There are several possible explanations for this:

(1) The excluded variable is less important in explaining the likelihood of success than the variables that were included in the model.

(2) The measure of the excluded variable was imperfect,or the data itself was imperfect.

(3) The range of values of the excluded parameter did not vary enough in this data set for its effect to be observed.

For example,the interburden competence was not found to be significant.This may have been because the geologic descriptions included with the core logs were not adequate to distinguish‘‘strong”from ‘‘weak”rock.In the Central Appalachian coalfields,some siltstones and even shales can be very strong[64].Moreover,since most of the case histories are all from CAP and the West,two coalfields where the rocks tend to be strong,there may not be suf-ficient variability in the data base to capture the effect of interburden competence.

Table 3 Pearson correlations between the parameters in the multiple seam database.

Table 4 Logistic regression results for the final model.

Table 5 Contingency table showing the performance of the multiple seam empirical model against the case histories (with probability cutoff=0.83).Green boxes are correct predictions,red boxes are misclassifications (incorrect predictions).

Fig.12.The effect of chosen probability cutoff on the performance of the multiple seam model.Sensitivity is the percent of successful cases that are correctly predicted;and specificity is the percentage of the failures that are correctly predicted.

The time lag since mining the previous seam was another variable that was not statistically significant.The data base contained a total of 12 overmining cases in which the time lag was less than 10 years.Of these,all but two were successes,indicating that time lag by itself is unlikely to be a major factor.However,one of the two failures proved to be one of the three outliers discussed earlier.It is possible in that case that the subsidence was delayed until after the active mine was developed,which would have resulted in a dynamic interaction.

The lack of influence of the interburden thickness to lower coal bed thickness ratio may also be due to the small number of relevant cases in the data base.There were 30 cases (21 development and 9 retreat)in which the interburden thickness was 7.5-10 times the lower coal bed thickness.Of these,13,or 44%,are failures,which is a relatively high failure rate.However,the failure likelihood may be predicted by other variables,particularly the interburden thickness,which was less than 15 m in all but one of these cases.It appears that the upper seam mining in these 30 cases probably took place in the fracture zone,above the top of the caving zone which is normally 6-10 seam heights above the lower bed (see Fig.7).It seems likely that once the upper seam is above the caving zone,the interburden thickness to lower coal bed thickness ratio may not be significant.However,since all of these cases (but one) came from just two mines in Virginia,it is possible that more failures could be encountered in other geologic environments.

Type of mining,development versus retreat,was another factor that was not significant in the final analysis.The effect of retreat mining is indirectly included in the total vertical stress variable,however.On average,the total vertical stress was only 20%greater in the retreat cases than in the development cases.

The model also does not include variables that simulate the interaction between parameters.For example,it seems likely that extra support might be more effective where the roof is weak.A variable that modeled the interaction between those two variables might be appropriate.However,the data base was just too small to support the inclusion of such variables.

9.Packaging the final design method

The first,essential attribute of an empirical method is that it provide reasonable,reliable,and useful guidance for engineering design.Table 5 and Fig.12 show that the final best multiple seam model can predict the severity of a multiple seam interaction with a high rate of accuracy.However,it would be difficult to employ Eq.(6),with the constant adjusted,directly in design.

The solution was to solve Eq.(6) for the interburden thickness.The resulting equation provides the critical interburden thickness(INTcrit) that the model predicts is required for the design to be a success (Eq.(7)).

One disadvantage of Eq.(7) is that,because it is a linear function,it can predict a negative value for the interburden thickness.Therefore,a second logistic regression model was determined using the natural log of the interburden (LnINT) rather than the interburden by itself.The resulting new logistic regression equation using LnINT was very similar to Eq.(6),but its ROC was slightly less at 0.88.This LnINT model was used to derive a second equation for the critical interburden thickness (Eq.(8)).

Fig.13 compares the Eqs.(7) and(8),and shows that the LnINT(Eq.(8))predicts more conservative values of the critical interburden when the predicted interburden is less than 18 m or so.The natural log equation also avoids negative critical interburden values.Since the linear interburden model fits the data slightly better,Eq.(7)is preferred when the predicted critical interburden exceeds 18 m.The final model therefore calculates the critical interburden using both equations,and then reports the value from Eq.(7) if it exceeds 18 m,otherwise it reports the value from Eq.(8).

Fig.14 shows the model’s predictions for the case history database.Where the actual interburden thickness exceeds the predicted interburden (INTcrit),the model predicts that the case should be a success.Failure is predicted when the actual interburden thickness is less than INTcrit.Fig.14 shows that just 11 of the failure case histories were misclassified as predicted successes,but that even those cases were close to the borderline.

Fig.13.Comparison between the linear and log predictive equations for a range of total vertical stress values,with all other variables fixed.

Fig.14.Performance of the multiple seam empirical model against the case history data base.

To apply the model in mine planning,it is useful to focus on the effect of supplemental support.Fig.15 again plots the model’s predictions of the critical interburden for the case history database,but this time cases having supplemental support are plotted as if no extra support was installed (the EX=0 condition).Those cases were extra support actually was installed are identified with different markers,however.

Three colored regions are defined in Fig.15.The uppermost green region is where success is predicted even when no extra support is installed.Within this‘‘Green region”,97%of the case histories were successful.In the middle,‘‘Yellow region”,success is predicted only if a pattern of supplemental support is installed.The lower boundary of this zone is established by adjusting the zone by applying the extra support component in the predictive Eqs.(7) and (8).Within the ‘‘Yellow zone”,85% of the cases that did install supplemental support were successful,while just 65%of those who did not install extra support succeeded.In the remaining bottom zone,or ‘‘Red region”of the diagram only 57%of the cases were successful.Therefore this zone should be considered one with a high probability of failure.Note,however,that even in the ‘‘Red region”,successful cases outnumber failures by 1.3-to-1.

Fig.16.The example multiple seam interaction problem described in the text.

The multiple seam model has been implemented in the Analysis of Coal Pillar Stability (ACPS) computer program [33].

Fig.16 shows a projected seven entry system that is being developed on 24 m by 24 m entry centers in a 1.8 m thick coal seam at a depth of 300 m.The entries are 6 m wide,and the CMRR of the immediate roof is 50.A coal seam located 30 m above the active seam was mined previously.A 25 m wide isolated remnant pillar,flanked by two 150 m wide fully extracted gob areas,lies directly above the projected entries.

ACPS shows that the single seam development stress for this case is 10.7 MPa,while the Lam2D model indicates that the multiple seam stress is 7.9 MPa.The total vertical stress is therefore 18.6 MPa.Using Eq.(7),the predicted critical interburden with Extra Support is

If no additional support is installed,the critical interburden is increased by 16.6 m,to 59.4 m.Since both of these values exceed the actual interburden of 30 m,the design falls into the‘‘Red zone”where the likelihood of failure is high.In addition,the pillar system SF is 1.42,which is less than the ACPS suggested value of 1.50.

One alternative is to modify the design by increasing the crosscut centers to 48 m and reducing the entry width to 5.2 m.This reduces the total vertical stress to 13.1 MPa,and the INTcrit (with Extra Support) to 23.6 m.The design is now in the ‘‘Yellow zone”where success is predicted if supplemental support is installed.The pillar system SF is also increased to 2.59.It should be noted that this modified design only needs to be implemented in the vicinity of the overlying isolated remnant pillar.

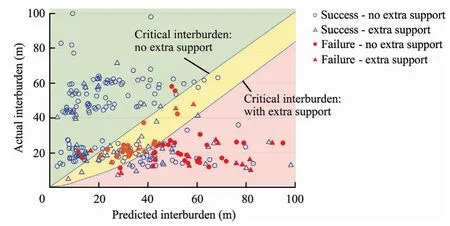
Fig.15.Effect of extra support in the multiple seam empirical model with the case histories.Green zone:predicted success even without extra support.Yellow zone:predicted success if extra support is installed.Red zone:predicted high probability of failure.

10.Conclusions

This paper has described in detail the process that was used to develop an empirical model of multiseam interactions.The mechanics of multiple seam mining were investigated,and four types of interactions were identified.Two of these,undermining and overmining,were selected for the model.

A large number of parameters were identified as being important to determining the intensity of multiple seam interactions.Some of these were easily measured,while new measures were developed for others.A two-level rating scale was developed for remnant structures,three geologic rating scales were employed,and the Lam2D numerical model was used to estimate multiple seam stresses.

The largest database of multiple seam case histories ever collected was central to the study.The original 2006 database was updated with the addition of cases from three new mines,which expanded its geographic diversity and extended it to lower CMRR roof.The statistical analysis found that overmining was found to be much more difficult than undermining,and that isolated remnant pillars caused more problems than gob-solid boundaries.Weaker roof was also found to significantly increase the likelihood of multiple seam interactions,while extra support reduced the risk.Many of the failed cases involved pillars whose SF appeared inadequate when the multiple seam stresses were accounted for in the evaluation.With statistical analysis it was possible to quantify these effects.Some factors that were not found to be statistically significant included the interburden competence,the time lag between mining the two seams,and the interburden thickness to lower coal bed thickness ratio.

The statistical model is embodied in regression equations that predict the likelihood of a severe multiple seam interaction.The model predicts the outcome in terms of three levels of risk:GREEN(where a major multiple seam interaction is considered unlikely),YELLOW(where adding a pattern of cable bolts or other equivalent supplemental support could greatly reduce the probability of a major interaction),or RED (a major interaction should be considered likely).The model has been implemented as a module in the Analysis of Coal Pillar Stability (ACPS) computer program.