单通道控制旋转弹角运动的复分析方法

陈成， 赵良玉， 谢浩怡， 郝晓兵

(1.北京理工大学 宇航学院, 北京 100081; 2.河南北方红阳机电有限公司, 河南 南阳 473000)

0 引言

由于绕自身纵轴的连续滚转，旋转弹在简化控制系统结构及组成、减小制造公差影响、避免单面烧蚀、降低成本等方面具有明显优势[1]，现已广泛应用于火箭弹、反坦克导弹、防空导弹、战略导弹等领域。考虑弹体的低通滤波特性，部分旋转弹仅使用一对鸭舵来完成俯仰和偏航两个方向的运动控制，进一步简化了弹体结构并降低了成本，如美国“拉姆”舰空导弹和我国FL-3000N近防系统就是这类单通道控制旋转弹的典型代表。

同样考虑连续滚转的特点，旋转弹飞行过程中会受到陀螺效应、马格努斯效应的影响，导致弹体纵轴绕速度矢量旋转并形成以速度矢量为中心的圆锥面运动，通常称为锥形运动或圆锥运动[2]。锥形运动将显著影响旋转弹飞行的动态稳定性，不收敛的锥形运动会导致射程降低甚至出现飞行中“掉弹”的情况[3]。因此，旋转弹的动态稳定性即锥形运动及其稳定条件，一直是国内外在旋转弹领域的研究重点和难点[4]。

目前，对旋转弹动态稳定性的研究主要围绕具有两对鸭舵的双通道控制旋转弹进行开展。由Murphy创造性提出的，在准弹体坐标系下建立复攻角运动模型对旋转弹角运动进行分析的方法至今仍被广泛采用，该方法能够给出弹体角运动稳定的解析式充要条件[5]。徐明友采用李雅普诺夫直接法得到旋转弹角运动的稳定边界条件，进一步证明了Murphy复攻角分析方法的正确性和有效性[6]。在此基础上，闫晓勇等[7]、杨树兴等[8]针对带有控制系统的制导火箭弹开展了深入研究，推导了不同自动驾驶仪结构下的旋转弹角运动稳定条件。与双通道控制旋转弹的解析研究方法不同，单通道控制旋转弹的研究更多是通过数值仿真来判断各因素对锥形运动稳定性的影响，这主要是因为其一对鸭舵引起的气动不对称性无法忽略[9]。任天荣等[10]通过对导弹纵向静稳定力矩及侧向力矩的研究，判断线性气动阻尼会对单通道控制旋转弹的锥形运动稳定产生不利影响。Cooper等[11]、石忠佼等[12]通过引入鸭舵坐标系，建立了具有一对鸭舵的单通道控制旋转弹线性化角运动模型，并利用数值计算得到了其锥形运动的稳定转速区间，揭示了气动不对称对单通道控制旋转弹角运动特性的影响规律。Xu等[13]建立了忽略二倍弹旋频率分量的单通道控制旋转弹非线性角运动模型，并通过李雅普诺夫指数谱分析和庞加莱截面分析，指出单通道控制旋转弹的规则锥形运动可以随参数变化过渡到混沌运动。

双通道控制旋转弹的研究成果证明了通过复攻角运动方程对弹体动态稳定性进行复分析是切实有效的，可得到旋转弹角运动的解析解并能够揭示弹体出现不收敛锥形运动的原因。但对于单通道控制旋转弹来说，受一对鸭舵引入的不对称气动力影响，导致无法直接建立其复攻角运动模型，也就无法采用复分析方法对其锥形运动稳定性进行研究，尽管Xu等[13]通过建立忽略二倍弹旋频率分量的单通道控制旋转弹角运动模型，消除了不对称因素的影响，推导得到了对应的复攻角运动模型，但其并未对该模型的准确性进行验证，且没有确定不同的舵面偏转方式对角运动的影响规律。

本文针对单通道控制旋转弹角运动分析方法的不足，在对比分析多个角运动近似模型的基础上，构建了适用于单通道控制旋转弹动态稳定性研究的复攻角运动模型，采用复分析方法得到了旋转弹无舵偏、固定舵偏及正弦式舵偏条件下的角运动解析解，并对角运动的收敛过程、稳态情况及可能出现的共振现象进行了分析，为研究同类旋转弹的锥形运动稳定性问题提供了参考。

1 角运动模型及稳定性分析

1.1 角运动模型

参考文献[11-12]，定义如图1所示的弹体坐标系Obxbybzb、鸭舵1坐标系Oc1xc1yc1zc1、鸭舵2坐标系Oc2xc2yc2zc2. 其中：δ为舵偏角。弹体坐标系原点Ob位于弹体质心，Obxb轴与弹体纵向对称轴重合；Obzb轴位于弹体纵向对称面内与Obxb轴垂直，指向下为正；Obyb轴垂直于Obxbzb平面，指向弹体右侧为正。鸭舵1坐标系原点Oc1位于鸭舵1的质心，Oc1xc1轴与鸭舵1纵向对称轴重合；Oc1zc1轴位于鸭舵1纵向对称平面内与Oc1xc1轴垂直，指向下为正；Oc1yc1轴垂直于Oc1xc1zc1平面，指向弹体右侧为正。鸭舵2坐标系原点Oc2位于鸭舵2的质心，Oc2xc2轴与鸭舵2纵向对称轴重合；Oc2zc2轴位于鸭舵2纵向对称平面内与Oc2xc2轴垂直，指向下为正；Oc2yc2轴垂直于Oc2xc2zc2平面，指向弹体右侧为正。

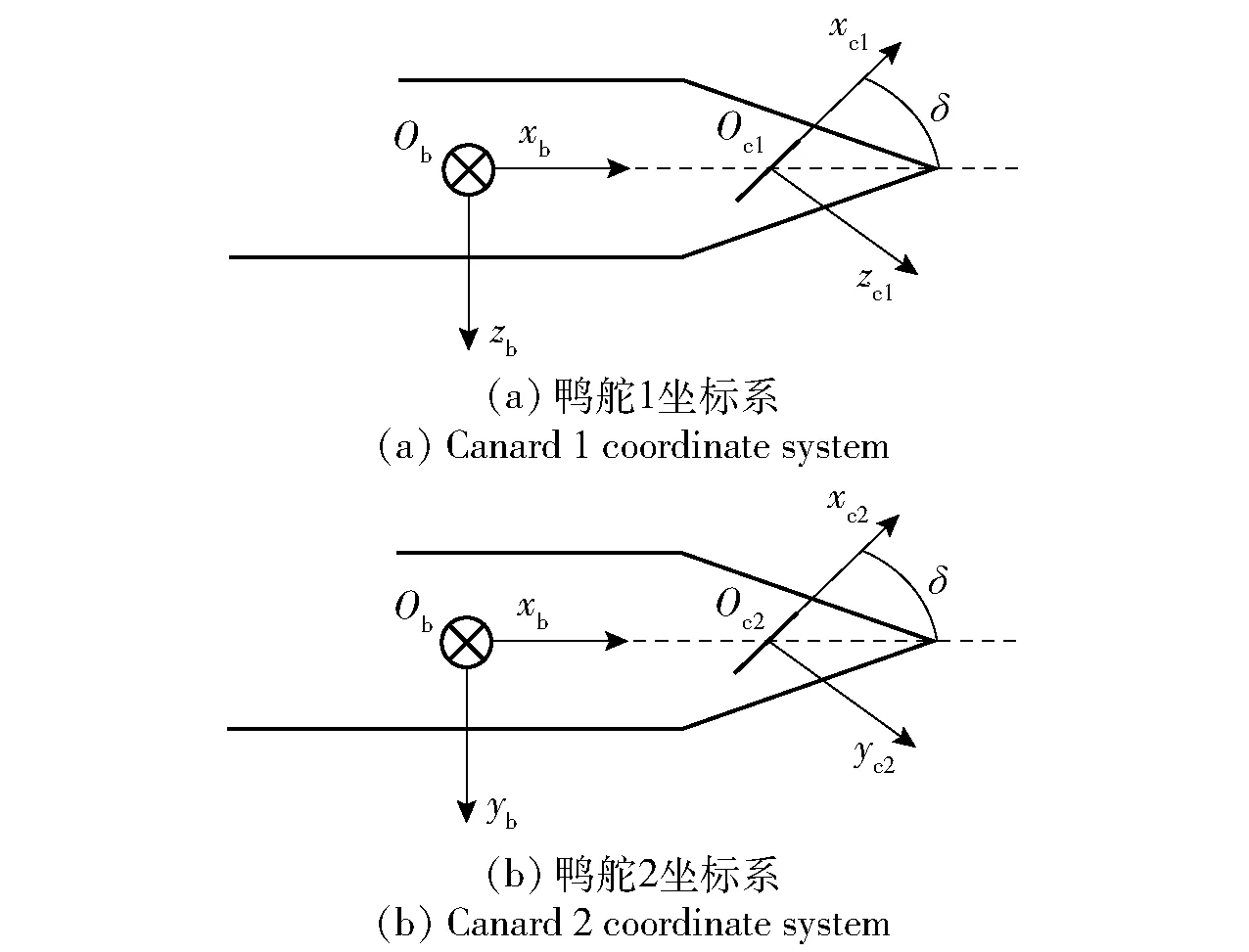
图1 鸭舵坐标系Fig.1 Canard coordinate system

假设弹体速度、转速、质量及气动力系数在短时间内保持不变，且满足sinα=α、cosα=1的小角度假设(α为攻角)，通过建立单通道控制旋转弹的动力学方程，可得其线性化角运动模型(下文称为单通道模型)：

(1)

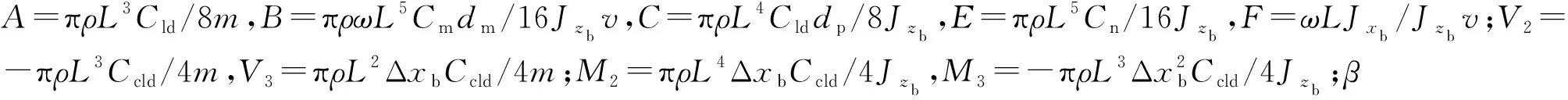
由(1)式的系统矩阵可以看出，仅具有一对鸭舵的单通道控制旋转弹，在飞行过程中会引入气动力不对称项，即vV2/L、V3、M2v2/L2、M3v/L，导致无法建立其复攻角形式的角运动方程。针对此问题，仿照双通道控制旋转弹的鸭舵布局引入另外一对虚拟鸭舵，并在该对鸭舵上建立如图(1)b所示的鸭舵2坐标系，令两对鸭舵的舵面偏转规律相同，如此可得到双通道控制形式的旋转弹角运动模型(下文称为双通道模型)：

(2)

由(2)式系统矩阵可知其具有气动对称性，若直接忽略(1)式中的气动力不对称项，同样可得满足气动对称性的角运动模型(下文称为单对称模型)：

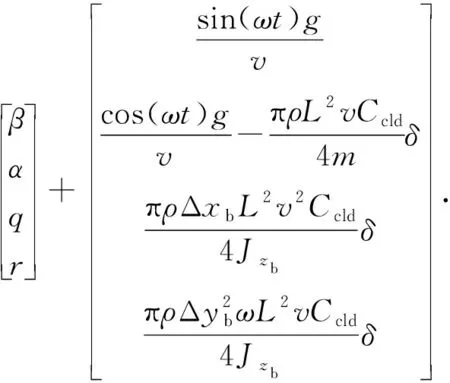
(3)

接下来利用(2)式和(3)式分析其角运动情况，以判断它们是否能够作为单通道控制旋转弹的角运动近似模型。

1.2 稳定性分析

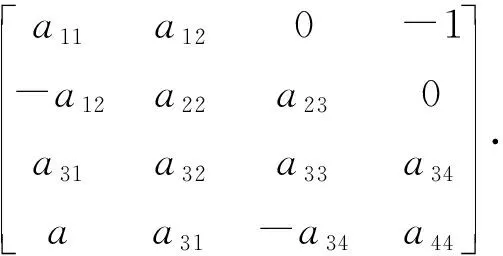
(4)

用(4)式表示单通道模型的系统矩阵，则系统的特征方程为

Δ(λ)=b4λ4+b3λ3+b2λ2+b1λ+b0，

(5)

式中：λ为特征方程的特征值；b4、b3、b2、b1、b0为系数，各项系数定义为

(6)

由劳斯判据可知其稳定的充要条件为

(7)

对于指定的单通道控制旋转弹，可将(6)式中的旋转弹锥形运动稳定条件等价为锥形运动稳定情况下的转速取值范围，将表1所示的相关参数代入(6)式，经转换求解得到单通道模型的稳定转速区间为

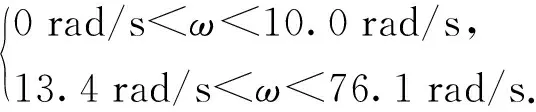
(8)

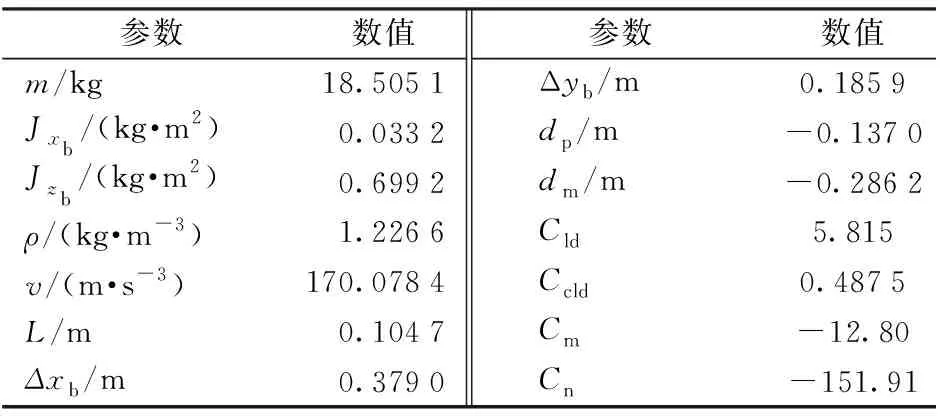
表1 弹体参数

同理可得单对称模型的稳定转速区间为

0 rad/s<ω<79.2 rad/s，

(9)

双通道模型的稳定转速区间为

0 rad/s<ω<69.0 rad/s.

(10)

为更好地比较上述3种模型，分别对不同转速条件下的角运动情况进行数值仿真。建立如图2所示的准弹体坐标系[12]：Onxn轴与弹体坐标系Obxb轴重合；Onzn轴位于包含弹体纵轴的铅垂面内，指向下为正；Onyn轴垂直于Onxnzn平面，指向弹体右侧为正。在准弹体坐标系下有准攻角α*和准侧滑角β*的表达式为

(11)

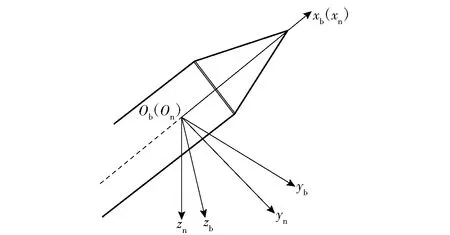
图2 坐标系示意图Fig.2 Schematic diagram of coordinate system

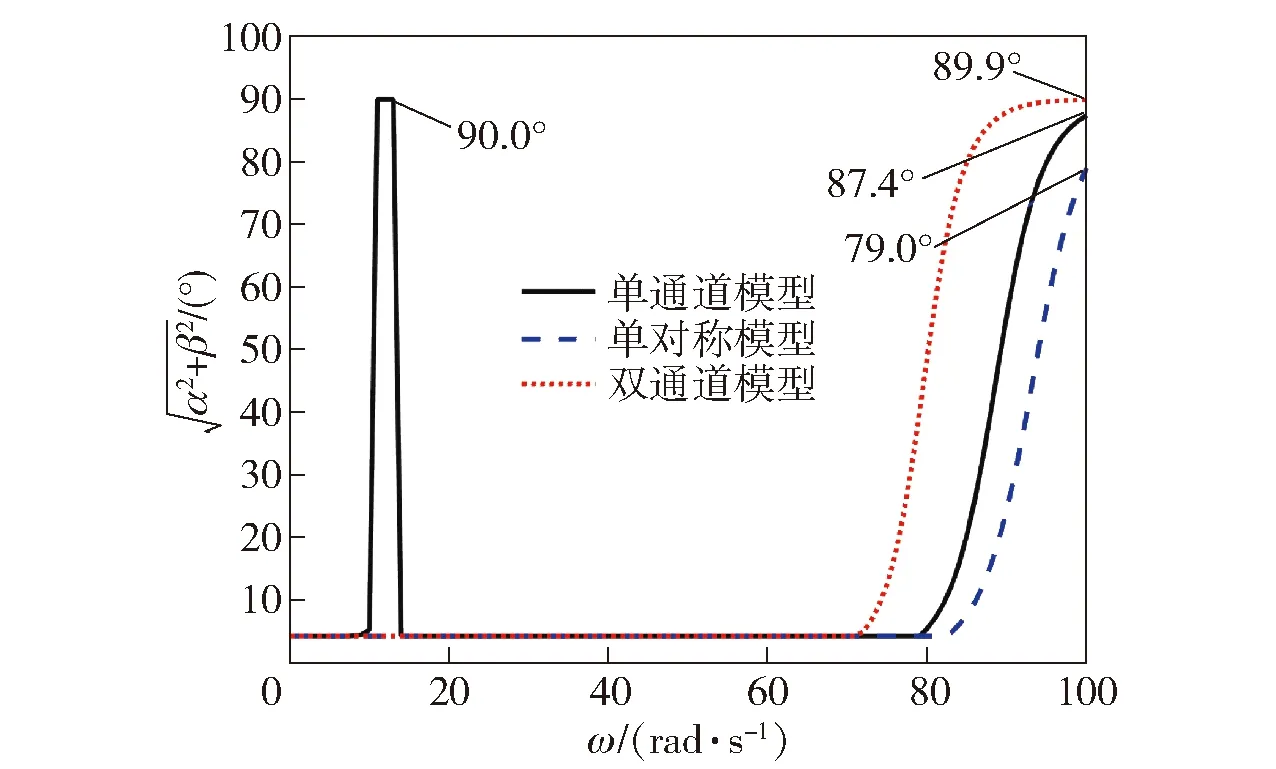
图3 0～100 rad/s转速条件下最大全攻角变化情况Fig.3 Full angle of attack at 0-100 rad/s

由(8)式的求解结果及图3的仿真结果可知，单通道模型的稳定转速区间不连续，在低频段存在10～13.4 rad/s的不稳定转速区间，且在该区间内角运动发散速度极快。除此之外，3种模型在临界转速以内的最大全攻角均相差不大，但超出临界转速后，最大全攻角的数值会出现明显差别。

分别对3种模型处于各自高频临界转速条件下的角运动情况进行仿真，结果见图4.

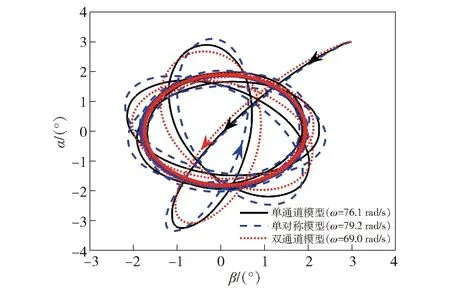
图4 稳定转速边界条件下的角运动曲线Fig.4 Angular motion curves at critical stable rotational speed

由图4及上述分析结果可知，舵偏角为0°时，3种模型在各自高频临界转速条件下的角运动曲线有一定相似，但近似度较差，且3种模型的高频临界转速相差较大，故单对称模型和双通道模型作为近似模型均存在不足，有必要构造更准确的角运动近似模型。

2 改进的角运动模型

2.1 单对称倍频模型

考虑旋转弹的低通滤波特性，在准弹体坐标系下建立忽略二倍弹旋频率分量的单通道控制旋转弹角运动模型[13](下文称为单对称倍频模型)：

(12)

同样利用劳斯判据可求得其稳定转速区间为

0 rad/s<ω<75.9 rad/s.

(13)

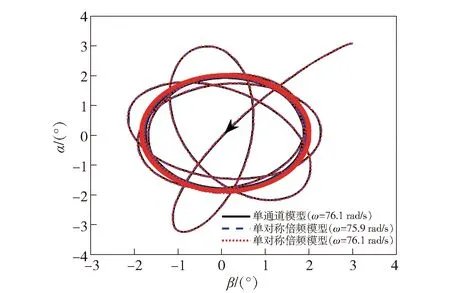
图5 稳定转速边界条件下的角运动曲线Fig.5 Angular motion curves at critical stable rotational speed

设攻角和侧滑角的仿真初值均为3°，舵偏角为0°，仿真时长30 s，单对称倍频模型的角运动情况如图5～图8所示。

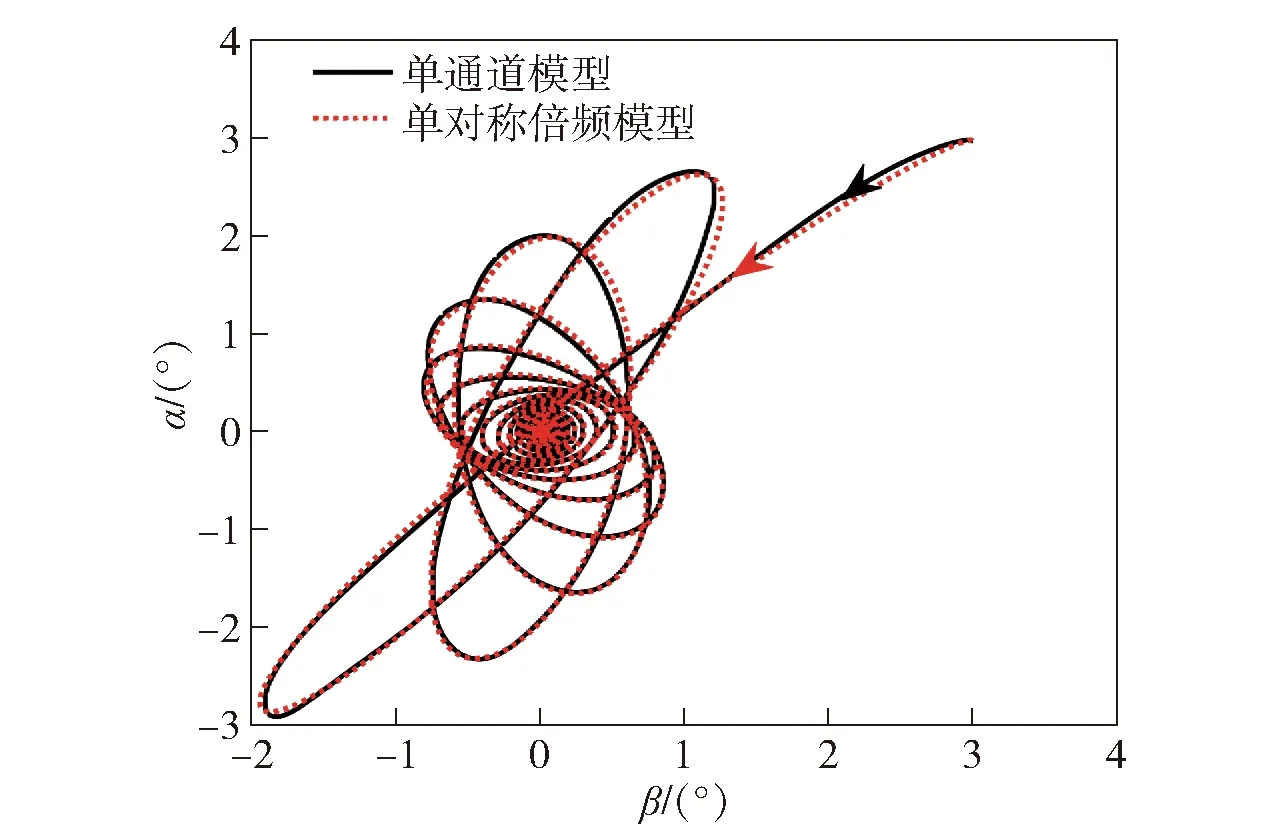
图6 30 rad/s转速条件下的角运动曲线Fig.6 Angular motion curves at 30 rad/s

图7 80 rad/s转速条件下的角运动曲线Fig.7 Angular motion curves at 80 rad/s

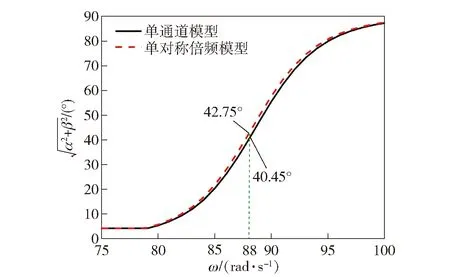
图8 75～100 rad/s转速条件下的最大全攻角Fig.8 Full angle of attack curves at 75-100 rad/s

根据图5和图6可知，单对称倍频模型的转速边界与单通道模型较为接近，且其在稳定转速区间内(除较低频段转速外)的角运动曲线与单通道模型也比较匹配。但文献[8]指出，若增加自动驾驶仪会减小旋转弹的动态稳定区域，因此有必要对其稳定转速区间外的角运动情况进行分析。由图7和图8可知，当弹体转速超出稳定转速时，单对称模型的角运动曲线与单通道模型相差较大，80 rad/s转速条件下前者的锥形运动频率明显快于后者，88 rad/s转速条件下的最大全攻角数值相差最大，为2.3°. 不同转速条件下的最大全攻角见表2.

表2 不同转速条件下的最大全攻角

2.2 单对称μ系数模型

对比上述4种模型的系统矩阵可以发现，其差异主要是由vV2/L、V3、M2v2/L2、M3v/L及其系数决定的，这些项均与鸭舵的升力/侧向力系数导数有关，构造具有气动对称性角运动近似模型的过程，实质上是对上述各气动不对称项系数进行调整的过程。参考前文所述各模型，对vV2/L、V3、M2v2/L2、M3v/L各项引入比例因子μ，在准弹体坐标系下构造更准确的单通道控制旋转弹角运动近似模型(下文称为单对称μ系数模型)，其形式如下：

(14)

为提高近似度，将单通道模型的临界转速ω=76.1 rad/s作为已知条件代入(14)式，可解得

μ=2.07.

(15)

对单对称μ系数模型的角运动情况进行仿真，结果如图9～图12所示。

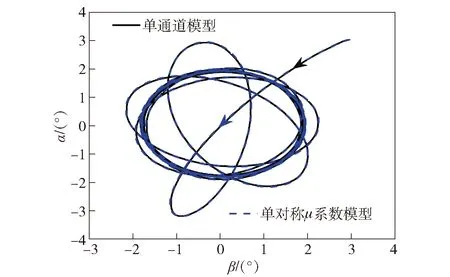
图9 76.1 rad/s临界转速条件下的角运动曲线Fig.9 Angular motion curves at 76.1 rad/s

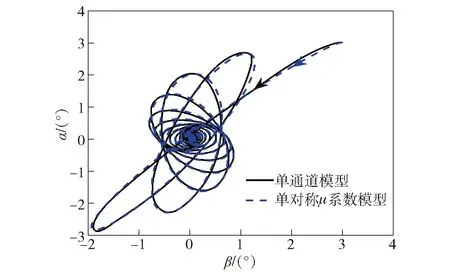
图10 30 rad/s转速条件下的角运动曲线Fig.10 Angular motion curves at 30 rad/s

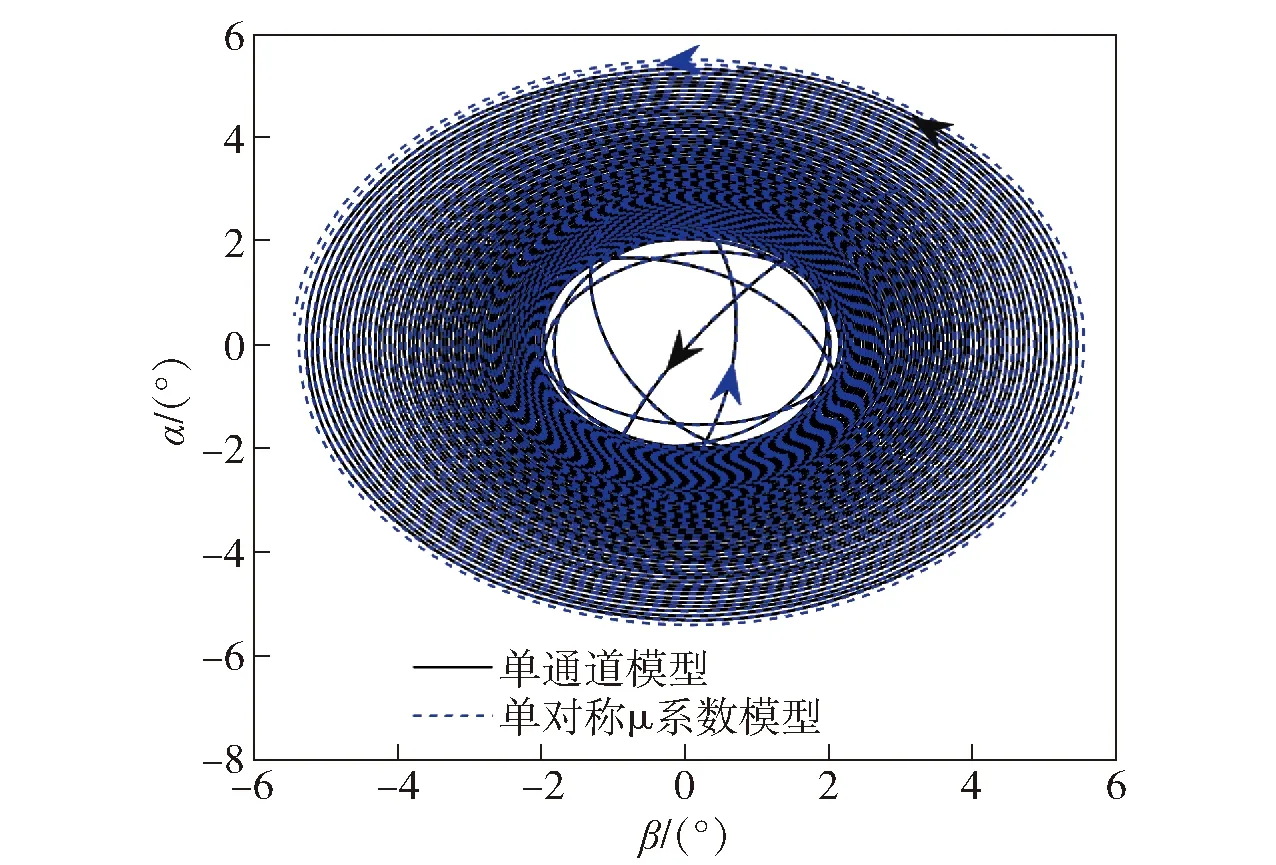
图11 80 rad/s转速条件下的角运动曲线Fig.11 Angular motion curves at 80 rad/s

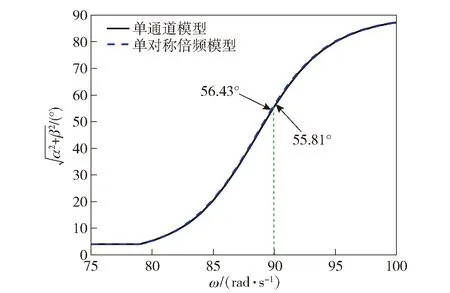
图12 75～100 rad/s转速条件下的最大全攻角Fig.12 Full angle of attack curves at 75-100 rad/s

由图9～图12仿真结果可知：当弹体转速在稳定转速区间内时(除较低频段转速外)，单对称μ系数模型的角运动情况同样十分接近单通道模型，且弹体转速超出稳定转速时，单对称μ系数模型的角运动情况要优于单对称倍频模型；80 rad/s转速条件下与单通道模型的锥形运动频率十分接近；90 rad/s转速条件下的最大全攻角数值相差最大，但仅为0.62°；不同转速条件下的最大全攻角数值均更接近于单通道模型，即单对称μ系数模型作为单通道控制旋转弹角运动近似模型更为准确。具体见表3.

表3 不同转速条件下的最大全攻角

3 复攻角运动模型及解析解

单通道控制旋转弹的执行机构常采用气动舵机和电动舵机，气动舵机一般作两位置或三位置的Bang-Bang式偏转运动，电动舵机一般作正弦式偏转运动。为验证单对称μ系数模型的有效性，通过推导其对应的复攻角运动方程，对无舵偏、固定舵偏及正弦式舵偏3种典型舵面偏转情况进行解析求解[14-16]，得到不同条件下的角运动稳态值，并对共振情况进行分析。

定义复攻角ξ为

ξ=β*+iα*.

(16)

参考(14)式中单对称μ系数模型的矩阵表达式，对于与其形式相似的如(17)式所示模型为

(17)

式中：a、d、e、f、j、h、u1、u2、u3、u4为用于简化形式的中间量。

比较(14)式，令(17)式中

(18)

式中：

(19)

有复攻角运动方程：

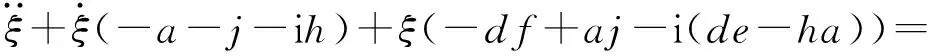
(20)

则(20)式可表示为

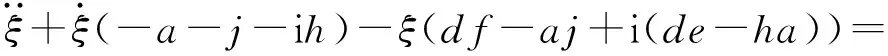
(21)

3.1 无舵面偏转

为了对(21)式中的复攻角运动方程进行解析求解，需要先确定其齐次方程的通解，再求取不同舵面偏转条件下的非齐次方程特解，二者相加即可得到复攻角运动方程的解析解。当考虑重力影响且无舵面偏转时，有

(22)

(22)式的特解为

(23)

则其通解表达式为

ξ=C1eφ1t+C2eφ2t+C3，

(24)

式中：

(25)

λ1、λ2为弹体角运动的圆运动阻尼指数，ω1、ω2为圆运动频率，并有

(26)

3.2 舵面偏转角度固定

当舵面偏转角度为某一固定值δ时，有复攻角运动方程：

(27)

(27)式的特解为

ξ*=C3eiωt+C4，

(28)

式中：

(29)

则其通解表达式为

ξ=C1eφ1t+C2eφ2t+C3eiωt+C4，

(30)

式中：

(31)

3.3 舵面正弦式偏转

当舵面作正弦式偏转时，可将舵偏角表示为

δ(t)=δmaxsin(kt+φ)，

(32)

式中：δmax为最大舵偏角；k为舵机控制频率；φ为初始相位。令k等于转速ω，则有复攻角运动方程：

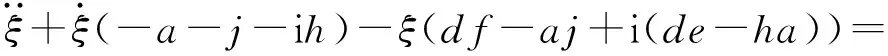
(33)

对(33)式进行化简，可得

(34)

(34)式的特解为

ξ*=C3e2iωt+C4，

(35)

式中：

(36)

则其通解表达式为

ξ=C1eφ1t+C2eφ2t+C3e2iωt+C4，

(37)

式中：

(38)

4 仿真分析

4.1 舵面偏转角度固定

根据(30)式的解析结果，当偏转角度固定时，由舵面偏转施加的控制可以视为周期性的强迫扰动，旋转弹角运动在无舵偏状态二圆运动的基础上增加了以转速为圆频率(幅值与舵偏角相关)的简谐运动，变成三圆运动，且在转速ω接近ω1或ω2时产生共振。将弹体参数及单对称μ系数模型中的各项代入(26)式，令ω=ω1或ω=ω2，可得

ω=11.90 rad/s.

(39)

尽管11.90 rad/s的低频段转速属于单对称μ系数模型匹配度较差的范围，但由解析结果可知在该转速下单对称μ系数模型会因共振出现不收敛的锥形运动，且由于处于非稳定转速区间，单通道模型同样会出现不收敛的锥形运动。

将参数及模型中的各项代入(27)式～(31)式，可得角运动的解析解。设攻角和侧滑角的仿真初值均为3°，仿真时长30 s，对不同固定舵偏及转速下的角运动情况进行仿真，仿真结果如图13～图16所示。

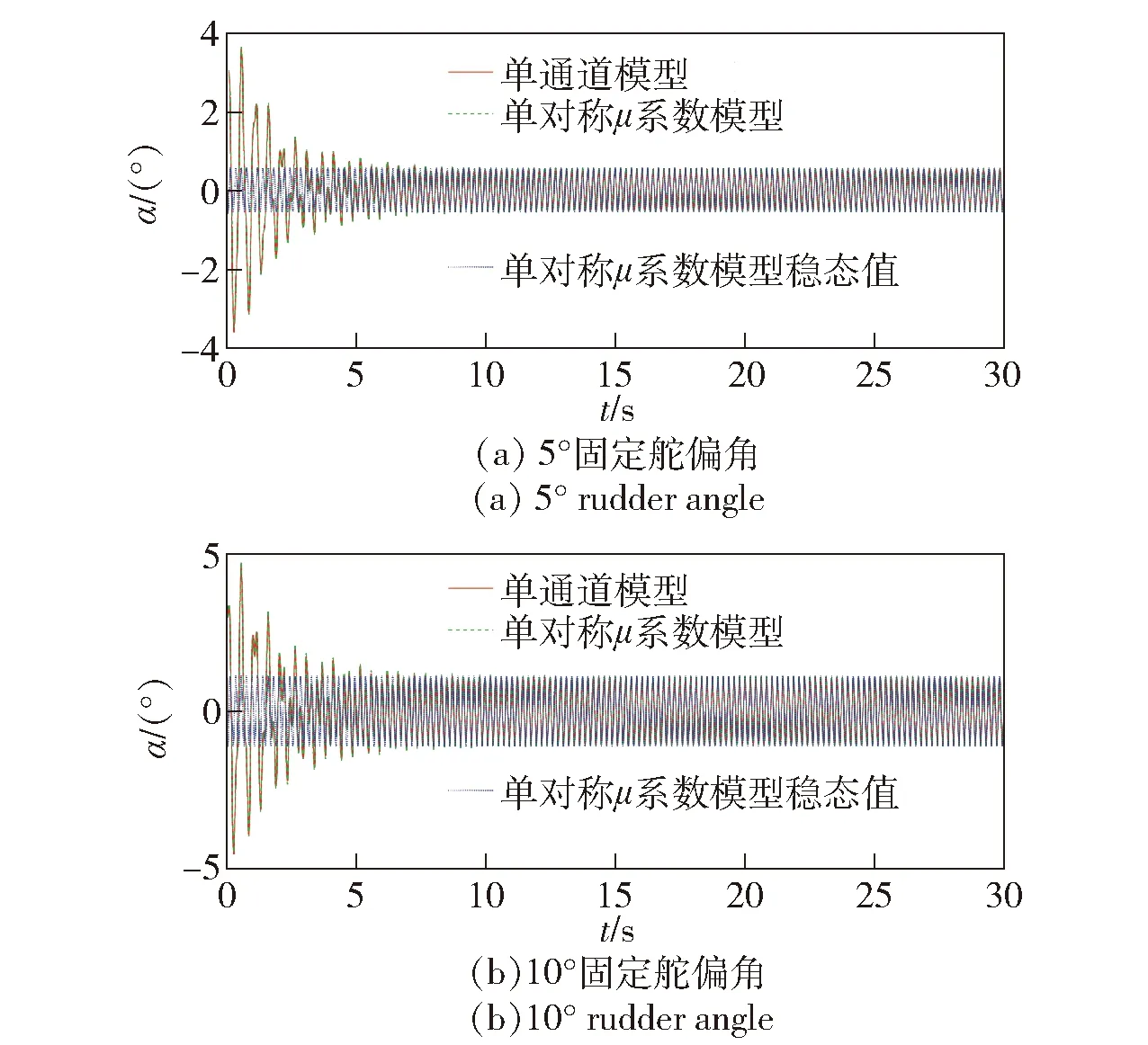
图13 30 rad/s转速条件下的攻角变化曲线Fig.13 Angle-of-attack curve at 30 rad/s

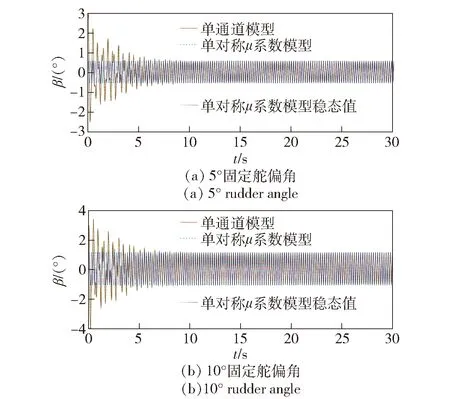
图14 30 rad/s转速条件下的侧滑角变化曲线Fig.14 Sideslip angle curve at 30 rad/s

图15 60 rad/s转速条件下的攻角变化曲线Fig.15 Angle-of-attack curve at 60 rad/s

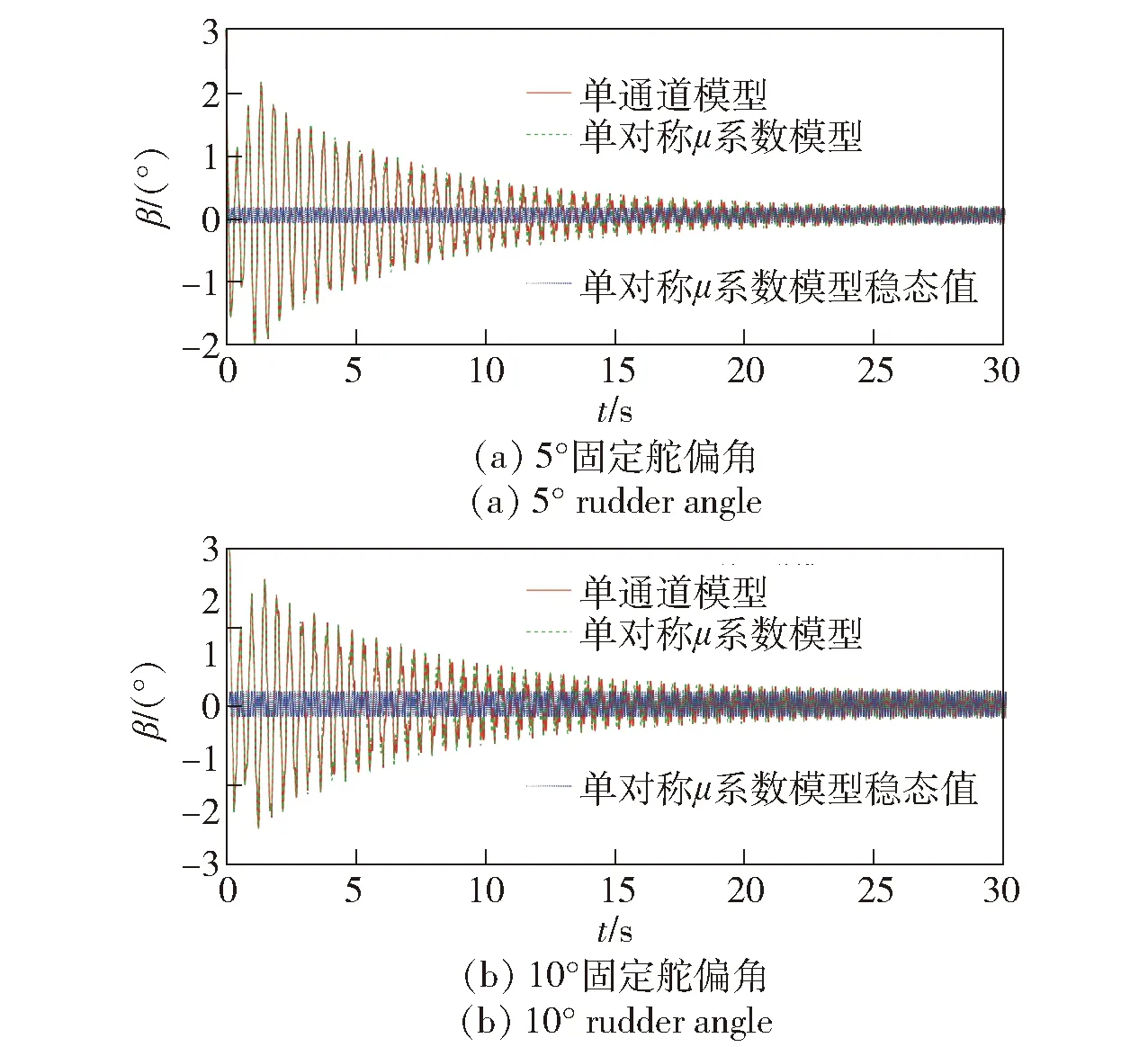
图16 60 rad/s转速条件下的侧滑角变化曲线Fig.16 Sideslip angle curve at 60 rad/s

由图13～图16仿真结果可以看出，不同固定舵偏及转速条件下，单对称μ系数模型的角运动曲线与单通道模型均匹配较好，且收敛趋势相同。对比图13(a)与图13(b)、图16(a)与图16(b)在相同转速、不同舵偏下的仿真结果可知，角运动的振幅随舵偏值的增大而增大；对比图13与图15、图14与图16在相同舵偏、不同转速下的仿真结果可知，转速较低时，角运动收敛速度更快。根据旋转弹旋转一周受等效控制力作用的原理，当舵偏角固定时，弹体旋转一周受到的等效控制力为0 N，角运动稳定后会做绕原点的强迫运动，与图13～图16中的仿真结果一致。

4.2 舵面正弦式偏转

根据(37)式，单对称μ系数模型在二倍转速接近ω1或ω2时会产生共振。将弹体参数及模型中的各项代入(26)式，令2ω=ω1或2ω=ω2，可得

ω=5.88 rad/s.

(40)

设最大舵偏角为10°，初始相位为60°，对转速为5.88 rad/s时的角运动情况及0～10 rad/s转速条件下的最大全攻角情况进行仿真，结果如图17和图18所示。

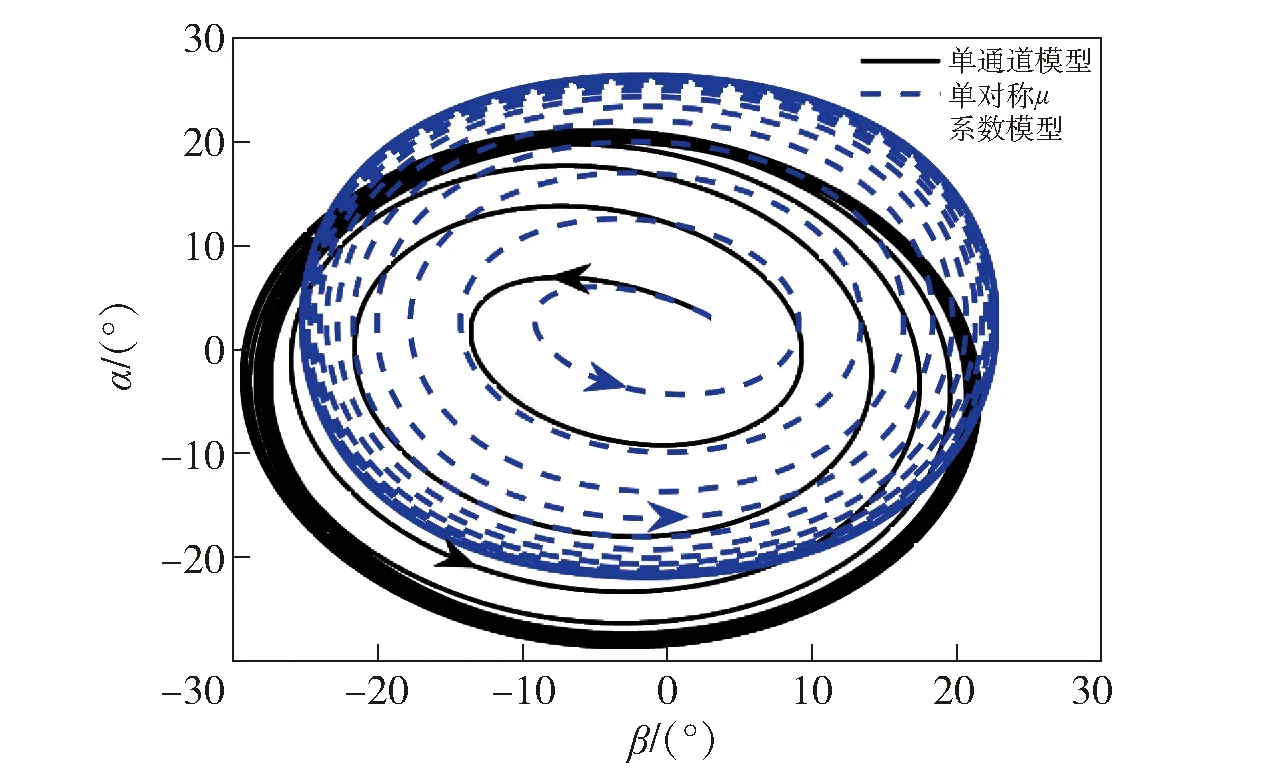
图17 5.88 rad/s转速条件下的角运动曲线Fig.17 Angular motion curves at 5.88 rad/s

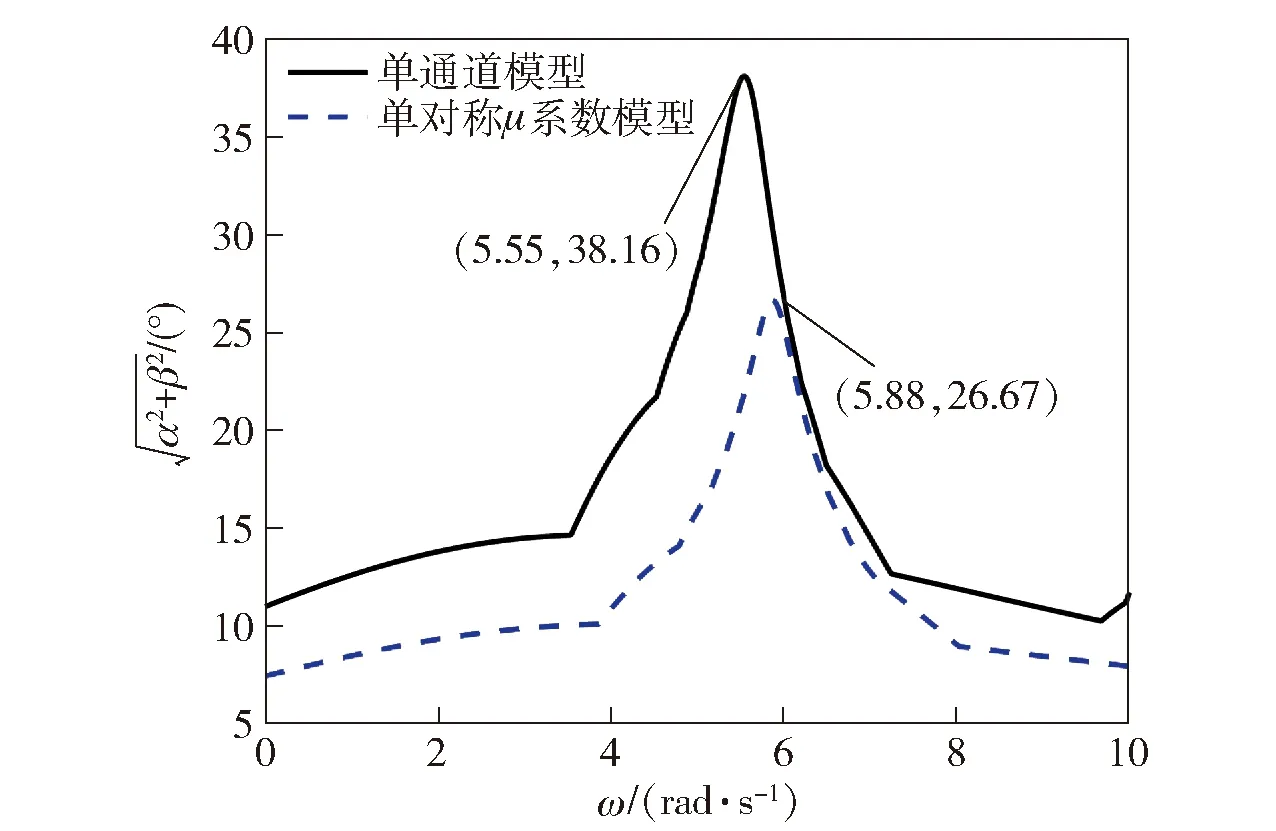
图18 0～10 rad/s转速条件下的最大全攻角Fig.18 Full angle-of-attack curves at 0-10 rad/s

由图17、图18的仿真结果可知，尽管在5.88 rad/s低频转速条件下，单对称μ系数模型的匹配度与高频段转速相比稍差一些，但两种模型均出现了共振(单通道模型具体共振转速为5.55 rad/s)，可见在舵面作正弦式偏转时，单对称μ系数模型的共振分析结果能够准确反映单通道控制旋转弹角运动的共振情况。

对不同最大舵偏角、初相位及转速条件下的角运动情况进行仿真，结果如图19～图22所示。

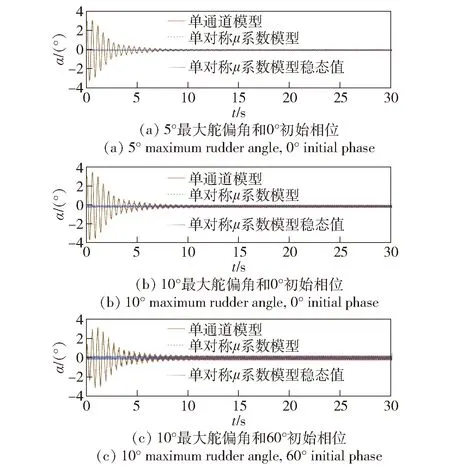
图19 30 rad/s转速条件下的攻角变化曲线Fig.19 Angle-of-attack curve at 30 rad/s

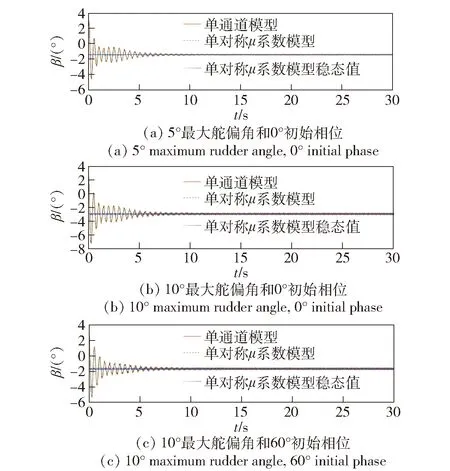
图20 30 rad/s转速条件下的侧滑角变化曲线Fig.20 Sideslip angle curve at 30 rad/s

图21 60 rad/s转速条件下的攻角变化曲线对比Fig.21 Angle-of-attack curve at 60 rad/s

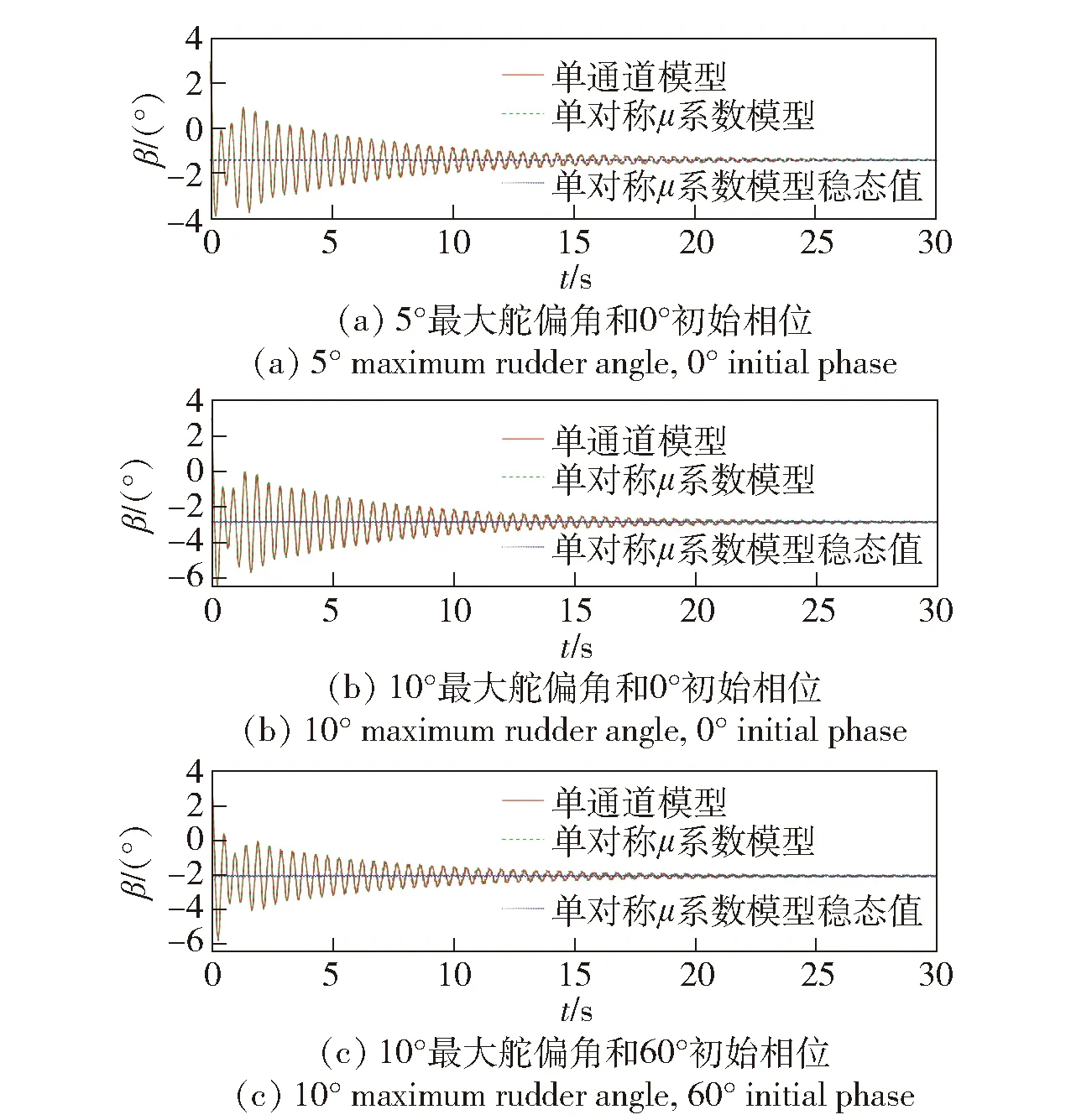
图22 60 rad/s转速条件下的侧滑角变化曲线Fig.22 Sideslip angle curve at 60 rad/s

由图19～图12的仿真结果可以看出，舵面作正弦式偏转时，在不同最大舵偏角及转速条件下，单对称μ系数模型的角运动曲线与单通道模型均匹配较好。对比图19(a)与图19(b)、图22(a)与图22(b)可知，角运动的振幅随最大舵偏角的增大而增大，角运动在转速较低时收敛速度更快。弹体旋转一周受到等效控制力的大小和方向与舵偏角幅值及初相位有关：初始相位为0°时，等效控制力的方向为Onyn轴负向；初始相位不为0°时，等效控制力在Onyn轴及Onzn轴上均有分量，控制力的分析结果与图19～图22中角运动的仿真收敛结果一致。

5 结论

本文针对单通道控制旋转弹角运动现有分析方法的不足，通过引入一个比例因子构建了具有气动对称形式的单对称μ系数模型，推导得到其复攻角运动方程。利用复分析方法得到了无舵偏、固定舵偏及正弦式舵偏情况下角运动的解析解，并对角运动的收敛过程、稳态情况及共振情况进行了分析。得到主要结论如下：

1) 在单通道控制旋转弹的稳定转速区间内(除较低频段转速外)，单对称倍频模型及单对称μ系数模型与单通道模型的近似度都很高，但超出高频段的稳定转速后，后者的准确性要明显优于前者。

2) 通过求解复攻角运动方程，可以得到单对称μ系数模型在不同舵面偏转情况下的角运动解析解，在固定舵偏及正弦式舵偏情况下，单对称μ系数模型与单通道模型的角运动曲线均匹配较好。

3) 无论是固定舵偏还是正弦式舵偏，均存在低频段共振转速，且单通道模型与单对称μ系数模型的共振转速在正弦式舵偏情况下基本吻合。

参考文献(References)

[1] 高庆丰. 旋转导弹飞行动力学与控制[M]. 北京: 中国宇航出版社, 2016.

GAO Q F. Flight dynamics and control of spinning missiles [M]. Beijing: China Astronautic Publishing House, 2016. (in Chinese)

[2] 任天荣, 马建敏. 旋转弹锥形运动发生区间及频率特性研究[J]. 固体火箭技术, 2014, 37(3): 295-300.

REN T R, MA J M. Research on activating region and frequency characteristics of coning motion for spinning missiles [J]. Journal of Solid Rocket Technology, 2014, 37(3): 295-300. (in Chinese)

[3] 段笑菊, 孙瑞胜, 白宏阳, 等. 锥形运动控制的导弹姿态稳定性分析[J]. 国防科技大学学报, 2015, 37(3): 97-103.

DUAN X J, SUN R S, BAI H Y, et al. Analysis on the altitude stability of missile with coning motion-based control [J]. Journal of National University of Defense Technology, 2015, 37(3): 97-103. (in Chinese)

[4] 陈亮, 刘荣忠, 郭锐, 等. 旋转尾翼弹箭极限圆锥运动稳定判据[J]. 兵工学报, 2019, 40(7): 1329-1339.

CHEN L, LIU R Z, GUO R, et al. Stability criteria for limiting conical motion of rotary fin-stablized projectiles [J]. Acta Armamentarii, 2019, 40(7): 1329-1339. (in Chinese)

[5] MURPHY C H. Free flight motion of symmetric missiles: R1216[R]. Aberdeen Proving Ground, MD, US: The Ballistic Research Laboratory, 1963.

[6] 徐明友. 用李雅普诺夫直接法建立弹箭飞行动稳定条件[J]. 南京理工大学学报, 2001, 25(1): 10-12.

XU M Y. Derivation of dynamical stability conditions of projectiles in flight by Lyapunov’s direct method [J]. Journal of Nanjing University of Science and Technology, 2001, 25(1): 10-12. (in Chinese)

[7] 闫晓勇, 杨树兴, 张成. 基于章动运动理论的火箭弹锥形运动稳定性分析[J]. 兵工学报, 2009, 30(10): 1291-1296.

YAN X Y, YANG S X, ZHANG C. Analysis of stability for coning motion of rockets based on theory of nutation movement [J]. Acta Armamentarii, 2009, 30(10): 1291-1296. (in Chinese)

[8] 杨树兴, 赵良玉, 闫晓勇. 旋转弹动态稳定性理论[M]. 北京: 国防工业出版社, 2014.

YANG S X, ZHAO L Y, YAN X Y. Dynamic stability of spinning missiles [M]. Beijing: National Defense Industry Press, 2014. (in Chinese)

[9] MURPHY C H. Angular motion of spinning almost-symmetric missiles [J]. Journal of Guidance, Control, and Dynamics, 1979, 2(6): 504-510.

[10] 任天荣, 马建敏. 基于陀螺力学的旋转导弹锥形运动分析[J]. 宇航学报, 2010, 31(9): 2082-2087.

REN T R, MA J M. Coning motion analysis of spinning missile based on gyrodynamics [J]. Journal of Astronautics, 2010, 31(9): 2082-2087. (in Chinese)

[11] COOPER G, FRESCONI F, COSTELLO M. Flight stability of an asymmetric projectile with activating canards [J]. Journal of Spacecraft and Rockets, 2012, 49(1): 130-135．

[12] 石忠佼, 谢浩怡, 林蔚, 等. 单通道控制的旋转弹锥形运动稳定性研究[J]. 固体火箭技术, 2015, 38(2): 156-159.

SHI Z J, XIE H Y, LIN W, et al. Research on coning motion stability of a spinning missile with one pair of canards [J]. Journal of Solid Rocket Technology, 2015, 38(2): 156-159. (in Chinese)

[13] XU Y L, YUE B Z, YANG Z M. Study on the chaotic dynamics in yaw-pitch-roll coupling of asymmetric rolling projectiles with nonlinear aerodynamics [J]. Nonlinear Dynamics, 2019, 97: 2739-2756.

[14] 吴映锋, 钟扬威, 王良明. 旋转稳定二维弹道修正弹在固定舵作用下的角运动特性研究[J]. 兵工学报, 2017, 38(7): 18-27.

WU Y F, ZHONG Y W, WANG L M. Study on angular motion characteristics of spin-stabilized 2D trajectory correction projectile under the effect of fixed canards [J]. Acta Armamentarii, 2017, 38(7): 18-27. (in Chinese)

[15] 常思江, 王中原, 刘铁铮. 鸭式布局双旋稳定弹强迫运动理论研究[J]. 兵工学报, 2016, 37(5): 829-839.

CHANG S J, WANG Z Y, LIU T Z. A theoretical study of forced motion for dual-spin-stabilized projectiles with canards [J]. Acta Armamentarii, 2016, 37(5): 829-839.(in Chinese)

[16] 杨杰, 谢飞, 常思江, 等. 小口径旋转稳定弹在控制作用下的弹道特性[J]. 兵器装备工程学报, 2020, 41(11):40-45.

YANG J, XIE F, CHANG S J, et al. Trajectory characteristics of small caliber spin-stabilized projectile under control [J]. Journal of Ordnance Equipment Engineering, 2020,41(11):40-45. (in Chinese)