面向弹丸炮口状态的自行火炮结构参数全局灵敏度

2021-04-08罗中峰管小荣徐诚

兵工学报 2021年2期

罗中峰，管小荣，徐诚

(南京理工大学机械工程学院，江苏南京 210094)

0 引言

研究自行火炮结构参数在给定分布条件下对弹丸炮口状态的敏感程度，有助于进一步精确降低弹丸炮口状态波动，提高自行火炮射击精度。进行自行火炮结构参数对弹丸炮口状态的敏感程度分析，首先需要建立自行火炮发射动力学模型。陈光宋[1]基于刚柔耦合和弹炮耦合约束方程建立了某自行火炮弹丸和身管耦合动力学理论模型。罗中峰等[2]基于有限段法建立了某自行火炮弹丸/身管相互作用模型。王晓锋等[3]通过凯恩方程和Huston方法建立了某自行火炮多体动力学模型。刘飞飞等[4]基于多体系统传递矩阵法和总传递方程自动推导定理，建立了某自行火炮行进间射击动力学方程。景鹏渊等[5]基于有限元法建立了某火炮发射动力学模型。上述建模方式存在以下问题：只进行弹丸/身管相互作用过程的建模，不能考虑自行火炮车体振动对弹丸膛内运动的影响；完全根据多刚体动力学理论建模，不能考虑弹丸的膛内运动；完全利用有限元理论建立自行火炮发射动力学模型，计算效率太低。

为了在面向弹丸炮口状态的自行火炮结构参数敏感程度分析过程中，充分考虑自行火炮参数的实际分布情况，需要使用全局灵敏度分析方法进行相关分析。Saltelli[6]经过研究发现:当相关变量按不同顺序产生时，该相关变量对目标函数方差的贡献是不同的。Saltelli等[[7]利用双层蒙特卡洛技术对单个相关变量的1阶和全敏感系数进行了估计。Kucherenko等[8]通过扩展敏感系数定义，推导了单个相关变量的1阶和全敏感系数的估计方法。Xu等[9]建议将相关变量的1阶敏感系数分解为相关和不相关两部分；同时还提供了一种当目标函数与输入变量为线性关系时，相关变量1阶敏感系数相关和不相关部分的计算方法。Li等[10]提供了一种当目标函数与输入变量为非线性关系时，相关变量1阶敏感系数相关和不相关部分的计算方法。Mara等[11]利用条件样本对相关变量组的敏感系数进行了估计。Tarantola等[12]利用傅里叶振幅敏度测试，对单个相关变量的敏感系数进行了估计。Decarlo等[13]根据贝叶斯校准数据，对单个相关变量的敏感系数进行了估计。Zhou等[14]基于样本间距离，对单个相关变量的敏感系数进行了估计。综上所述，当前全局灵敏度分析方法存在估计效率低和处理复杂等问题。

为了克服上述问题，本文首先建立能够同时考虑弹丸膛内运动和车体振动的某自行火炮整体发射动力学模型；然后给出一种基于Rosenblatt转换理论的全局灵敏度估计方法；最后基于上述模型和方法，进行面向弹丸炮口状态的某自行火炮结构参数全局灵敏度分析。

1 自行火炮整体发射动力学模型

1.1 弹丸炮口状态定义

为了获得完整的弹丸炮口位置和姿态，参照6自由度弹丸外弹道方程[15]的输入要求，构建弹丸炮口位置和姿态表征方法，如图1所示。

图1 弹丸炮口位置和姿态Fig.1 Position and attitude of projectile at muzzle

由于身管和弹丸间相互作用的结束，所以弹丸在炮口时(弹丸尾部到达炮口)可以认为是刚体。为了便于区别，作如下定义：图1所涉及的弹丸质心称为炮口质心，其为刚体弹丸质心；对应的弹轴称为炮口弹轴，其为刚体弹丸弹轴；弹丸在炮口时，炮口质心速度和水平面的夹角与火炮高低射角之差为弹丸炮口高低偏角，炮口质心速度与射击面的夹角为弹丸炮口方向偏角，炮口弹轴和水平面的夹角与火炮高低射角之差为弹丸炮口高低摆角, 炮口弹轴与射击面的夹角为弹丸炮口方向摆角，绕炮口弹轴的弹丸自转角为弹丸炮口自转角。

1.2 自行火炮整体发射动力学模型

建模前，作如下假设：不考虑供输弹动作对车体的激励作用；自行火炮在水平和静止状态下进行射击；在射击过程中，所有车轮处于制动状态，悬架处于开锁状态；地面为松软土壤地面。

为了获得较准确的弹丸炮口状态，建立了某自行火炮整体发射动力学模型。该模型由弹丸/身管相互作用模型和自行火炮发射动力学模型组成。弹丸/身管相互作用模型用于考虑弹丸膛内运动；自行火炮发射动力学模型用于考虑发射过程中的车体振动。弹丸/身管相互作用模型首先计算一个积分步，并在结果收敛条件下将获得的身管与高低机和摇架与耳轴连接处的受力、位移、速度和加速度输入到自行火炮发射动力学模型；其次自行火炮发射动力学模型以上述输入为基础计算一个积分步，并在结果收敛条件下将获得的身管与高低机和摇架与耳轴连接处的受力和位移、速度，加速度传递给弹丸/身管相互作用模型；最后弹丸/身管相互作用模型再次计算。如此循环，直到弹丸膛内运动结束。弹丸膛内运动结束，只运行自行火炮发射动力学模型。弹丸炮口状态由弹丸/身管相互作用模型计算得到。

1.2.1 弹丸/身管相互作用模型

1.2.1.1 弹丸膛内状态定义

为了获得弹丸炮口位置和姿态，参照图1构建弹丸膛内位置和姿态的表征方法，如图2所示。

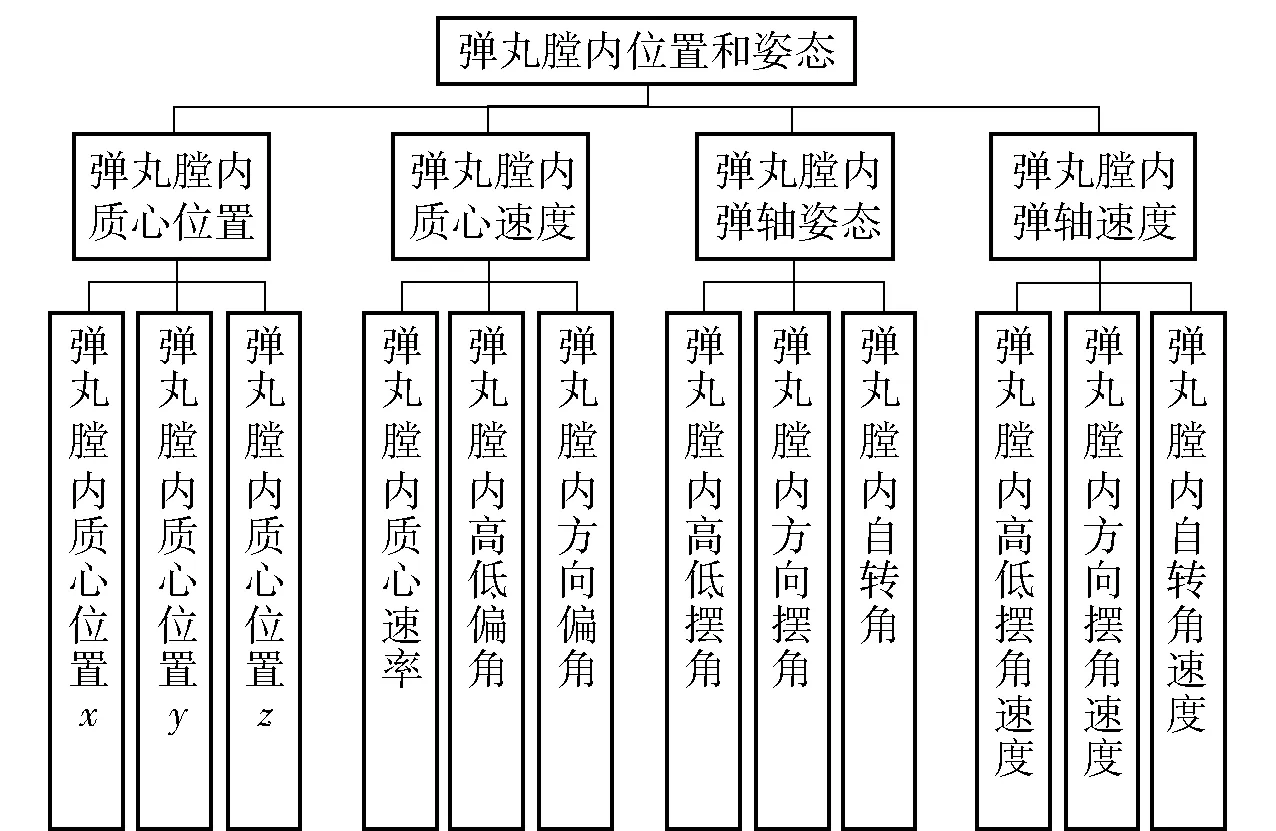
图2 弹丸膛内位置和姿态Fig.2 Position and attitude of projectile in bore

由于身管和弹丸间的相互作用，弹丸在身管中运动时存在弹性变形，其质心和弹轴是不确定的。为了计算需要，作如下定义：图2所涉及的弹丸质心称为膛内质心，它是弹丸为刚体时其质心所在点(该点随着弹丸的变形会发生位置变化)；相应的弹轴称为膛内弹轴，其经过膛内质心，垂直于该质心所在弹丸横截面；弹丸在身管中运动时，膛内质心速度和水平面的夹角与火炮高低射角之差为弹丸膛内高低偏角，膛内质心速度与射击面的夹角为弹丸膛内方向偏角，膛内弹轴和水平面的夹角与火炮高低射角之差为弹丸膛内高低摆角，膛内弹轴与射击面的夹角为弹丸膛内方向摆角，绕膛内弹轴的弹丸自转角为弹丸膛内自转角。

当弹丸到达炮口时，图2所示的弹丸膛内位置和姿态就会和图1所示的弹丸炮口位置和姿态对应相等。原因是：当弹丸到达炮口时，由于身管和弹丸间相互作用的结束，弹丸由柔性体变成刚体，弹丸膛内质心和膛内弹轴就分别会与弹丸炮口质心和炮口弹轴重合。基于上述原因，在计算过程中通过持续记录膛内质心和膛内弹轴位置变化情况，就可以计算出弹丸炮口的位置和姿态。

1.2.1.2 弹丸/身管相互作用模型

为了考虑弹丸的膛内运动，根据有限段思想建立了如图3[2]和图4[2]所示弹丸/身管相互作用模型。弹丸/身管相互作用模型的建模详情见文献[2]。

图3 身管半剖有限段模型Fig.3 Half sectional mesh model of barrel

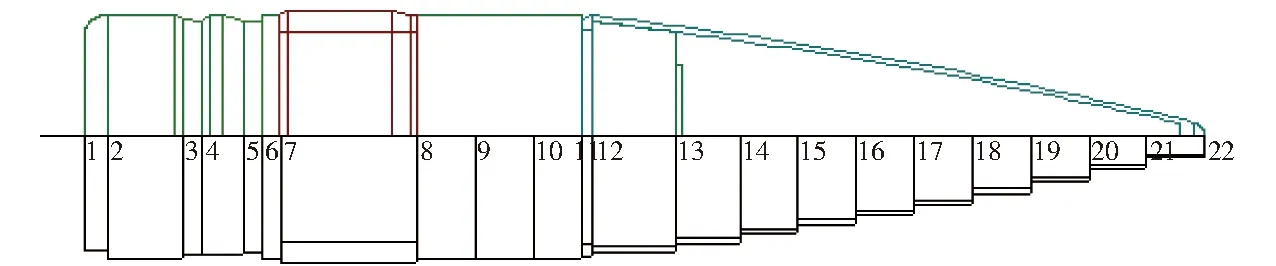
图4 弹丸半剖有限段模型Fig.4 Half sectional mesh model of projectile

1.2.2 自行火炮发射动力学模型

为了考虑发射过程中自行火炮车体振动，基于Adams软件建立了如图5所示某自行火炮发射动力学模型。

图5 某自行火炮发射动力学模型Fig.5 Launch dynamics model of a self-propelled gun

1.2.2.1 模型拓扑结构

图5所示自行火炮发射动力学模型的拓扑关系如图6所示。在图6中，hl(l=1,2,…,15)表示部件与部件之间的连接方式和载荷作用关系。其中：轮胎与地面间通过摩擦副进行连接，二者之间的载荷包括水平摩擦力和垂直压力；车轮与车身间通过弹簧和阻尼进行连接，二者之间的载荷包括弹簧力和阻尼力；炮塔与车身间通过衬套进行连接，二者之间的载荷包括旋转扭矩和接触压力；摇架与炮塔间通过旋转副进行连接，二者之间的载荷包括旋转扭矩和后坐力；反后坐装置中后坐部分与摇架间通过滑动副进行连接，反后坐装置中制退机和复进机部分与摇架固联；身管与反后坐装置中制退机和复进机固联在一起；身管与炮口制退器固联在一起；身管和高低机通过套箍连接在一起，身管和套箍固联在一起，套箍和高低机通过旋转副连接；高低机与炮塔间直接通过旋转副连接。

图6 某自行火炮发射动力学模型拓扑图Fig.6 Launch dynamics model topography of a self-propelled gun

1.2.2.2 碰撞力计算

为了考虑身管与高低机连接处因间隙产生的碰撞，上述自行火炮发射动力学模型根据(1)式所示Lankarani-Nikravesh模型[16]进行相关碰撞力的计算。

(1)

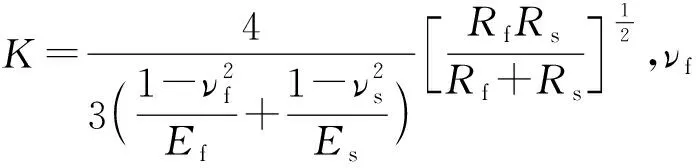
1.2.2.3 地面与轮胎间的接触力计算

为了准确计算地面与轮胎间的接触力，上述自行火炮发射动力学模型根据(2)式所示Wong-Reece模型[17]进行相关接触力的计算。

(2)

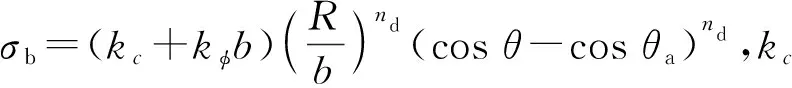
1.3 模型验证

在公开文献中尚没有某自行火炮弹丸炮口状态的测量数据。根据现有数据，通过特定条件下某自行火炮底盘和炮口垂直振动位移的测量值和计算值的对比，实现对上述自行火炮整体发射动力学模型的验证。在表1所示条件下，某自行火炮底盘和炮口垂直振动位移的测量值和计算值分别如图7和图8所示(图7所示测量值源于文献[18])。由图7和图8可知，在表1所示条件下，某自行火炮底盘和炮口垂直振动位移的测量值与其对应的计算值相对误差较小。所以上述某自行火炮整体发射动力学模型是可信的。

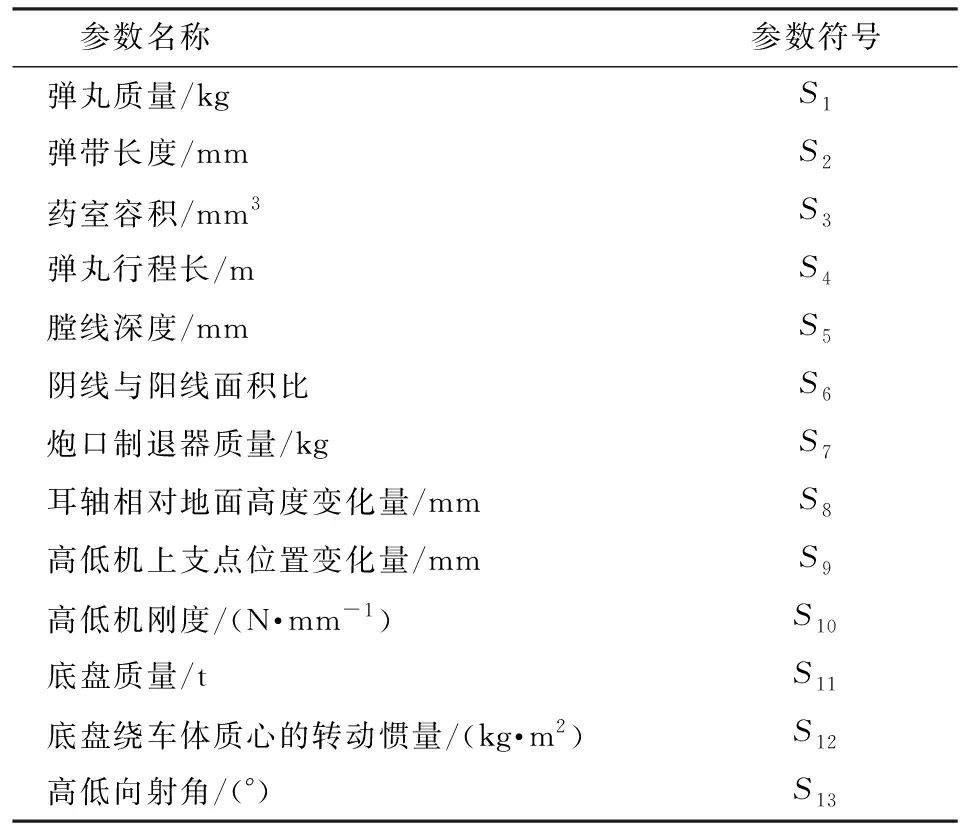
表1 参数列表

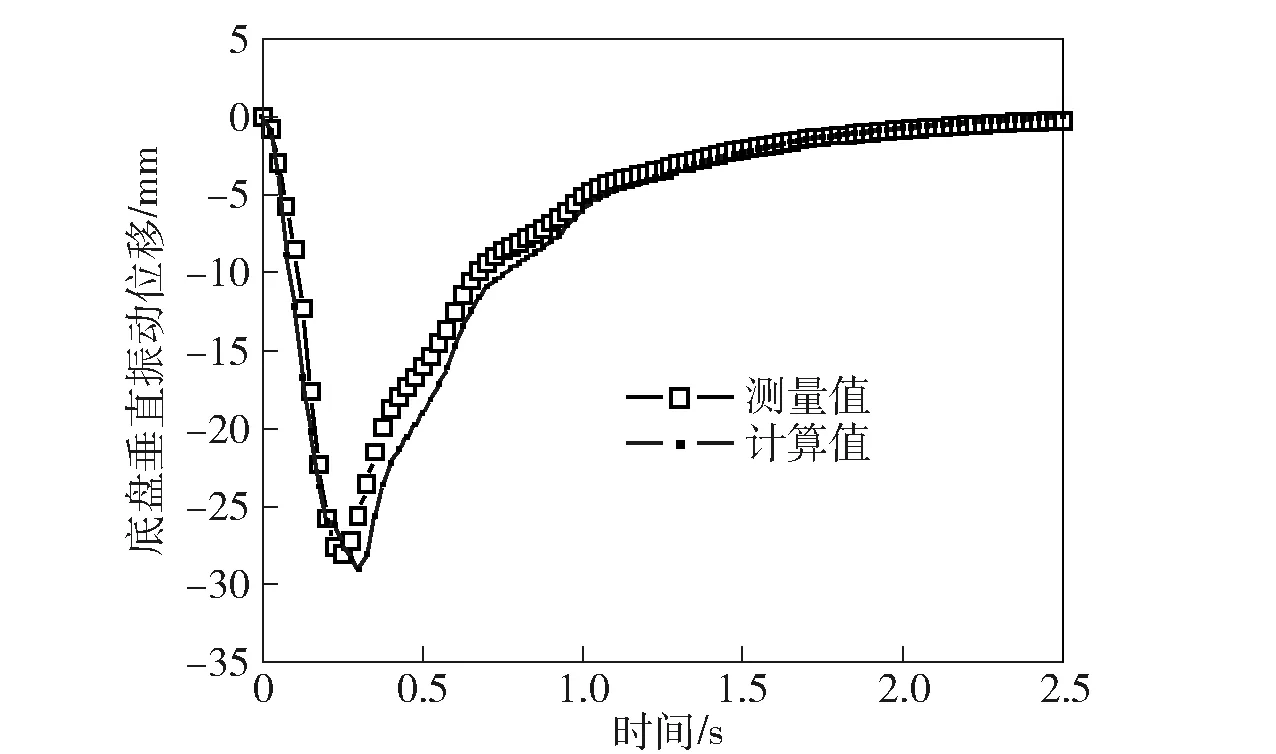
图7 底盘垂直振动位移对比图Fig.7 Measured and calculated vertical vibration displacements of chassis

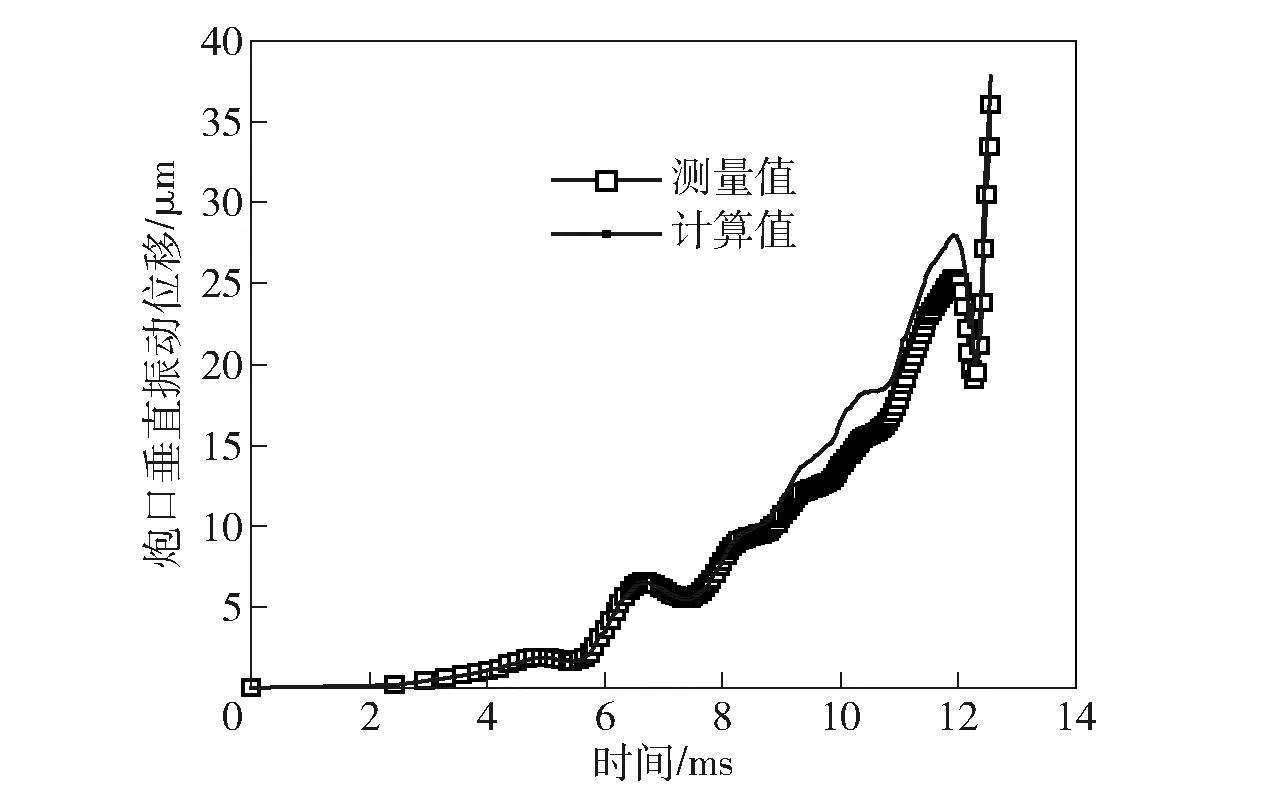
图8 炮口垂直振动位移对比图Fig.8 Measured and calculated vertical vibration displacements of muzzle

2 基于Rosenblatt转换理论的全局灵敏度分析方法

为了在自行火炮结构参数对弹丸炮口状态的敏感程度分析过程中，充分考虑自行火炮参数的实际分布情况，并克服当前全局灵敏度分析方法估计效率低和处理复杂等问题，本节以Sobol敏感系数定义为基础发展一种全局灵敏度分析方法。

2.1 敏感系数定义

本节所考虑的目标函数如(3)式所示。

Z=F(x1,…,xi-1,xi,xi+1,…,xn),

(3)

式中：x=[x1,…,xi-1,xi,xi+1,…,xn]是一个连续实随机向量，i=1,2,…,n，其联合概率密度函数为h(x).w是包含前i个输入变量的变量组，w=[x1,x2,…,xi]；w-是包含除前i个输出变量以外所有输入变量的变量组，w-=[xi+1,xi+2,…,xn]。

假设(3)式所示目标函数拥有有限方差。当(3)式所示目标函数拥有有限方差时，其方差V(Z)可以按(4)式[11]进行分解。

V(Z)=V[E[F(x)|w]]+

E[V[F(x)|(w|w-)]]=

V[E[F(x)|w-]]+

E[V[F(x)|(w-|w)]]，

(4)

式中：E(·)为函数期望；F(x)|w为在给定变量组w条件下F(x)的取值；w|w-为在给定变量组w-的条件下变量组w的取值。

为了衡量变量组w对目标函数方差的影响，有(5)式[11]和(6)式[11]所示定义。(5)式所示比率为变量组w的1阶敏感系数。

(5)

式中：hw-|w(w-)是变量组w-在给定w条件下的概率密度函数;hw(w)是变量组w的概率密度函数；R为实数集，R(i)表示本次积分对i个实变量进行积分，R(n-i)表示本次积分对n-i个实变量进行积分。该敏感系数用于记录由变量组w引发，变量组w和变量xi+1,xi+2,…,xn单独，对目标函数方差V(Z)的贡献率。

(6)式所示比率为变量组w的全敏感系数。

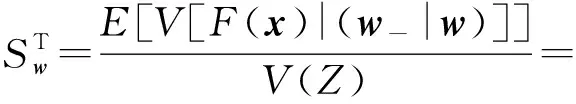
(6)

该敏感系数用于记录由w引发，变量组w和变量xi+1,xi+2,…,xn的单独项和它们的交叉项，对目标函数方差V(Z)的贡献率。

当x1,x2,…,xn都是独立变量时，(4)式可以转换成(7)式[6]，(5)式可以转换成(8)式[6]，(6)式可以转换成(9)式[6]。

V(Z)=V[E[F(x)|w]]+E[V[F(x)|w]]=
V[E[F(x)|w-]]+E[V[F(x)|w-]]，

(7)

(8)

式中：hxk(xk)为变量xk的边缘概率密度函数，k=1，2，…，n.

(9)

在后续段落中，视x1,x2,…,xn为相关变量。

2.2 相关变量的产生

2.2.1 相关变量的产生

根据Rosenblatt转换[19]，有(10)式成立。

(10)

式中：ui是均匀分布于[0,1]的独立实随机变量；Hxi|u(xi)是在给定变量集u⊆[x1,…,xi-1,xi+1,…,xn]的条件下，随机变量xi的分布函数；Hxi|u是单调增函数。

对(10)式所含各式进行求反，有(11)式成立。

(11)

同样根据Rosenblatt转换规则[19]，有(12)式成立。

(12)

式中：Gyi(yi)是连续独立实随机变量yi的分布函数。

(12)式代入到(11)式，有(13)式成立。

(13)

由(13)式可知：连续实向量x=[x1,…,xi-1,xi,xi+1,…,xn]可以用任意连续独立实向量y=[y1,…,yi-1,yi,yi+1,…,yn]表示。当向量x中变量的顺序发生变化时，变量xi的条件分布函数会发生变化，(13)式所示对应关系也会发生变化。

调整向量x中各个随机变量的顺序，得到x=[xi,x1,…,xi-1,xi+1,…,xn]。参照(13)式，有(14)式成立。

(14)

2.2.2 相关变量产生性质分析

当参照(14)式产生相关变量时，根据概率密度函数的性质[11]，相关变量(组)的分布情况如(15)式所示。

在条件概率密度函数的条件[11]下，向量x的联合概率密度函数有(16)式所示形式。

参照(16)式所示联合概率密度函数的任意一种形式产生w和w-时，均有x～h(x)、w～hw(w)和w-～hw-|w(w-)成立。参照(16)式所示联合概率密度函数的任意一种形式产生w和w-，根据(5)式和(6)式计算w的1阶敏感系数和全敏感系数时，h(x)、hw(w)、hw-|w(w-)、目标函数和积分域都是一致的。所以有如下结论：不管参照(16)式所示联合概率密度函数的何种形式产生w和w-，并以此为基础根据(5)式和(6)式计算w的1阶敏感系数和全敏感系数，获得w的1阶敏感系数和全敏感系数是唯一的，都是w的1阶敏感系数和全敏感系数。

综上所述，可以参照(16)式所示x联合概率密度函数的一种形式获得w和w-，并以此为基础根据(5)式和(6)式计算w的1阶敏感系数和全敏感系数。下面将以(14)式基础，进行w的1阶敏感系数和全敏感系数的估计研究。

(15)

式中：hxi|u(xi)为在给定u⊆[x1,…,xi-1,xi+1,…,xn]的条件下，相关变量xi的概率密度函数。

h(x)=hw(w)hw-|w(w-),

(16)

其中

式中：相关变量组w包含i个变量，hw(w)有i!种表达形式；相关变量组w-包含n-i个变量，hw-|w(w-)有(n-i)!种表达形式；h(x)有i!(n-i)!种表达形式。

(17)

2.3 敏感系数转化

(14)式代入(3)式，有(18)式成立。

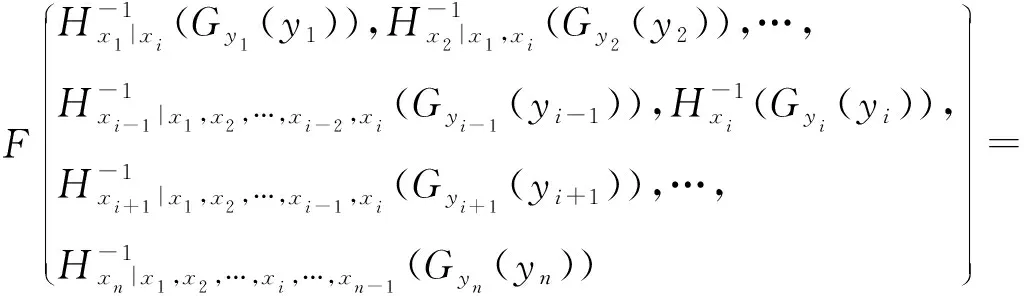
(18)

式中：y为包含独立随机变量y1，y2，…，yn的变量集，y=[y1,y2,…,yn];v为包含独立随机变量y1，y2，…，yi的变量集，v=[y1,y2,…,yi];v-为包含独立随机变量y′i+1，yi+2，…，yn的变量集，v-=[yi+1,yi+2,…,yn]。

由(14)式取反，可得(19)式。

(19)

对(19)式所含各式两边同时微分，根据概率密度函数的性质[20]，有(20)式成立。

(20)

式中：gyi(yi)为连续独立实随机变量yi的概率密度函数。

(20)式中前i个等式相乘，有(21)式成立。

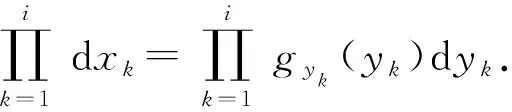
(21)

根据条件概率密度函数的性质[11]，有(22)式成立。

hx1,x2,…,xi(x1,x2,…,xi)=hxi(xi)hx1|xi(x1)·
hx2|x1,xi(x2)…hxi-1|x1,x2,…,xi-2,xi(xi-1)，

(22)

式中：hx1,x2,…,xi(x1,x2,…,xi)为相关变量x1,x2,…,xi的联合概率概率函数。

w=[x1,x2,…,xi]代入(22)式，有(23)式成立。

hw(w)=hxi(xi)hx1|xi(x1)hx2|x1,xi(x2)…·
hxi-1|x1,x2,…,xi-2,xi(xi-1).

(23)

因为w=[x1,x2,…,xi]，有(24)式成立。

(24)

(23)式和(24)式代入(21)式，有(25)式成立。

(25)

(20)式中第i+1个到第n个等式相乘，有(26)式成立。

(26)

根据条件概率密度函数的性质[11]，有(27)式成立。

hxi+1,xi+2,…,xn|x1,x2,…,xi(xi+1,xi+2,…,xn)=
hxi+1|x1,x2,…,xi-1,xi(xi+1)…hxn|x1,x2,…,xi,…,xn-1(xn)，

(27)

式中：hxi+1,xi+2,…,xn|x1,x2,…,xi(xi+1,xi+2,…,xn)是给定变量x1,x2,…,xi条件下，变量xi+1,xi+2,…,xn的联合概率密度函数。

w=[x1,x2,…,xi]和w-=[xi+1,xi+2,…,xn]代入(27)式，有(28)式成立。

hw-w(w-)=hxi+1|x1,x2,…,xi-1,xi(xi+1)…·
hxn|x1,x2,…,xi,…,xn-1(xn).

(28)

因为w-=[xi+1,xi+2,…,xn]，有(29)式成立。

(29)

(28)式、(29)式代入(26)式，可得(30)式。

(30)

2.3.1 相关变量组1阶敏感系数转化

(18)式、(25)式和(30)式代入(5)式，相关变量组w的1阶敏感系数定义式可由(5)式转换成(31)式。

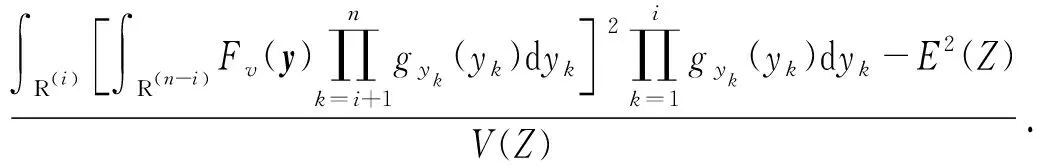
(31)

参考(8)式，目标函数由F变成Fv时，独立变量组v的1阶敏感系数定义式如(32)式所示。

Sv|F=Fv=

(32)

式中：Sv|F=Fv为目标函数由F变成Fv时，独立变量组v的1阶敏感系数。

比较(31)式和(32)式，有(33)式成立。

Sw=Sv|F=Fv.

(33)

(33)式表明：相关变量组w的1阶敏感系数可以转化成，目标函数由F变成Fv条件下，独立变量组v的1阶敏感系数。

2.3.2 相关变量组全敏感系数转化

(18)式、(25)式和(30)式代入(6)式，相关变量组w全敏感系数的定义式可由(6)式变成(34)式。

(34)

参考(9)式，目标函数由F变成Fv时，独立变量组v全敏感系数定义式如(35)式所示。

(35)

比较(34)式和(35)式，有(36)式成立。

(36)

(36)式表明：相关变量组w的全敏感系数可以转化成，目标函数由F变成Fv条件下，独立变量组v的全敏感系数。

2.3.3 敏感系数性质分析

1) 当w包含任意相关变量时，可以先参照

(10)式～(13)式进行变量转换(要求w包含的变量要先于其他变量被产生)，并将目标函数依照上述关系进行转换；转换后，w所包含相关变量对应独立变量组的敏感系数就是w的敏感系数(在(10)式～(13)式中，xi和yi是一一对应的)。

2) 当w只包含一个相关变量时，w-包含其余相关变量时，就可以参照上述方法进行单个相关变量的1阶敏感系数和全敏感系数的转化。因此：单个相关变量的1阶敏感系数是相关变量组1阶敏感系数的一种特殊情况；单个相关变量的全敏感系数是相关变量组全敏感系数的一种特殊情况。

2.4 估计样本的产生

为了实现对(5)式和(6)式所示敏感参数的估计，只需先产生两组独立变量yi的样本。具体步骤如下：1)根据独立变量yi的分布，利用蒙特卡洛法[21]，产生独立变量yi的样本；2)重复上述步骤，再次产生变量yi的样本。详细的取样结果如2.5节中矩阵A和B所示。

2.5 敏感系数估计

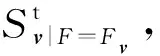
(37)

式中：yri为变量yi第1次取样的第r个样本;m为样本总数;y′ri为变量yi第2次取样的第r个样本。

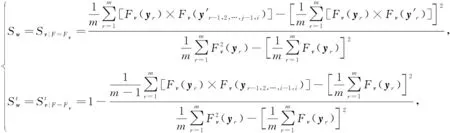
(38)

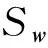
3 面向弹丸炮口状态的自行火炮结构参数全局灵敏度分析

为了降低面向弹丸炮口状态的自行火炮结构参数全局灵敏度分析的计算量，首先进行面向射击精度的弹丸炮口状态全局灵敏度分析，找出对射击精度影响较大的弹丸炮口状态特征量；然后以上述影响较大的特征量表征弹丸炮口状态，进行面向弹丸炮口状态的自行火炮结构参数全局灵敏度分析。

3.1 面向射击精度的弹丸炮口状态全局灵敏度分析

面向射击精度的弹丸炮口状态全局灵敏度分析过程如下：首先基于表2所示对弹丸炮口状态影响相对较大参数的分布情况，在第1节所示自行火炮整体发射动力学模型的帮助下，利用蒙特卡洛法统计出最大射程条件下弹丸炮口状态的分布情况(结果如表3所示)；然后基于6自由度弹丸外弹道方程[15]和表3所示弹丸炮口状态分布，在第2节所示全局灵敏度分析方法的帮助下，分别进行最大射程条件下面向弹丸落点纵向位移和横向位移的弹丸炮口状态全局灵敏度分析(结果见图9和图10)。

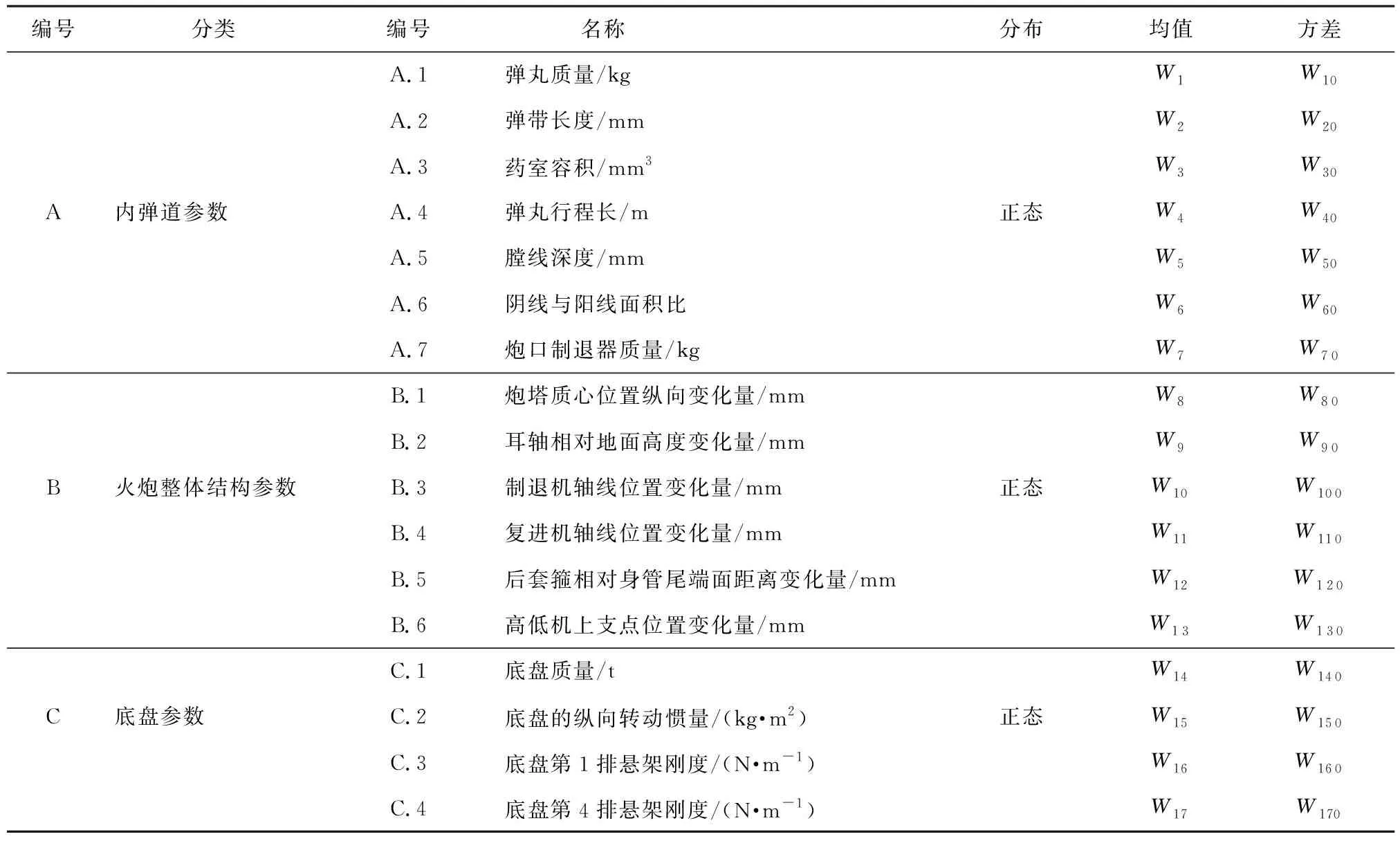
表2 参数分布

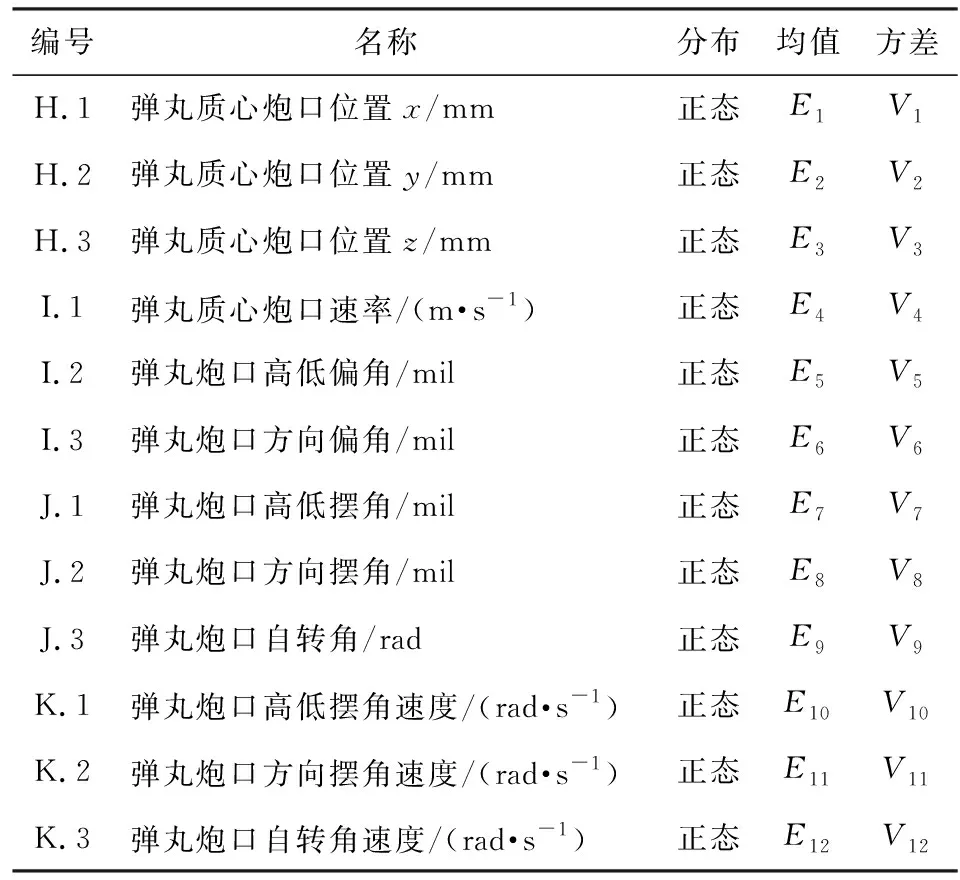
表3 弹丸炮口状态分布

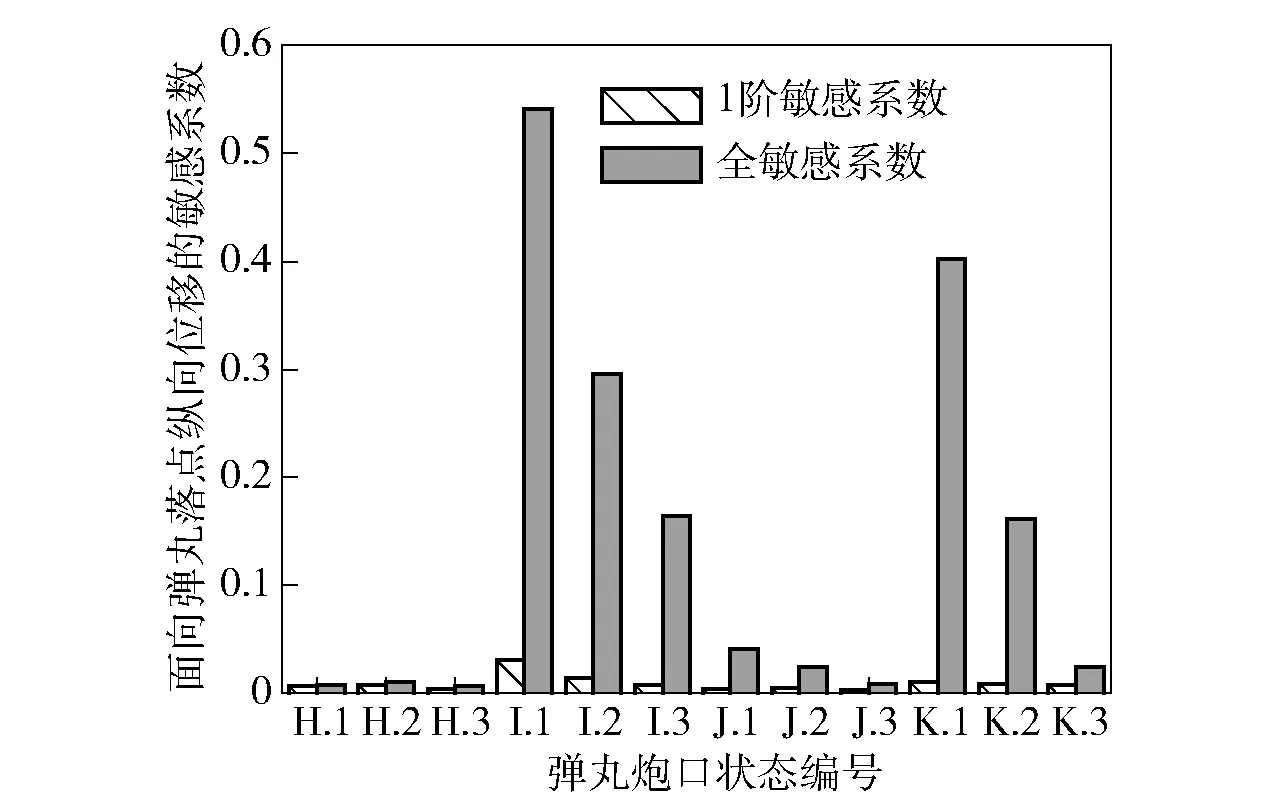
图9 弹丸炮口状态的敏感系数Fig.9 Sensitivity coefficients of projectile muzzle state

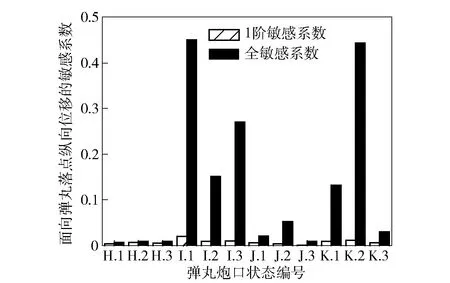
图10 弹丸炮口状态的敏感系数Fig.10 Sensitivity coefficients of position and attitude of projectile at nmuzzle

由图9和图10可知：弹丸炮口状态所包含各特征量的1阶敏感系数都比较小，同时它们的全敏感系数相对较大。造成这种现象的原因是，弹丸炮口状态各个特征量主要通过它们之间的交叉项作用于最大射程条件下弹丸落点纵向和横向位移。鉴于上述现象，可以通过图9和图10所示弹丸炮口状态各特征量的全敏感系数，比较它们对最大射程条件下弹丸落点纵向(横向)位移的敏感程度。根据上述分析，有如下结论：在表2所示条件下，弹丸质心炮口速率、弹丸炮口高低偏角、弹丸炮口方向偏角、弹丸炮口高低摆角速度和弹丸炮口方向摆角速度是影响某自行火炮最大射程条件下射击精度的主要弹丸炮口状态特征量。

3.2 面向弹丸炮口状态的自行火炮结构参数全局灵敏度分析

根据3.1节的分析结果，为了减少计算量，本节将以对自行火炮射击精度影响较大的弹丸炮口状态特征量(弹丸质心炮口速率、弹丸炮口高低偏角、弹丸炮口方向偏角、弹丸炮口高低摆角速度和弹丸炮口方向摆角速度)作为弹丸炮口状态的表征量，并以此为基础进行面向弹丸炮口状态的自行火炮结构参数全局灵敏度分析。

鉴于弹丸炮口状态服从多元正态分布的情况(如表3所示)，根据(39)式计算弹丸炮口状态的波动情况。

(39)

式中:Fj是对射击精度影响较大的弹丸炮口状态特征量；αj是Fj的权重系数；E(Fj)是Fj的均值；V(Fj)是Fj的方差。F越大，弹丸炮口状态波动越大；F越小，弹丸炮口状态波动越小。在本例中，计算所需的均值和方差如表3所示。因为最大射程条件下，弹丸落点纵向位移波动相对其横向位移波动较大，相关弹丸炮口状态特征量的权重系数直接取其最大射程条件下面向弹丸落点纵向位移的全敏感系数。

以弹丸炮口状态波动为分析目标，表2所示参数为分析变量，某自行火炮最大射程条件下面向弹丸炮口状态的全局灵敏度分析结果如图11和图12所示。在图11和图12中：自行火炮结构参数的1阶敏感系数也都比较小，同时它们的全敏感系数也相对较大；相对内弹道参数，火炮整体结构参数和底盘参数的全敏感系数要大一些。造成火炮整体结构结构参数和底盘参数的全敏感系数较大的原因是：内弹道参数加工精度高，公差范围小；火炮结构和底盘参数不易控制，波动范围大。

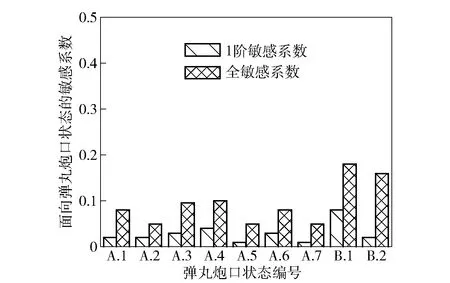
图11 结构参数敏感系数Fig.11 Sensitivity coefficients of structural parameters

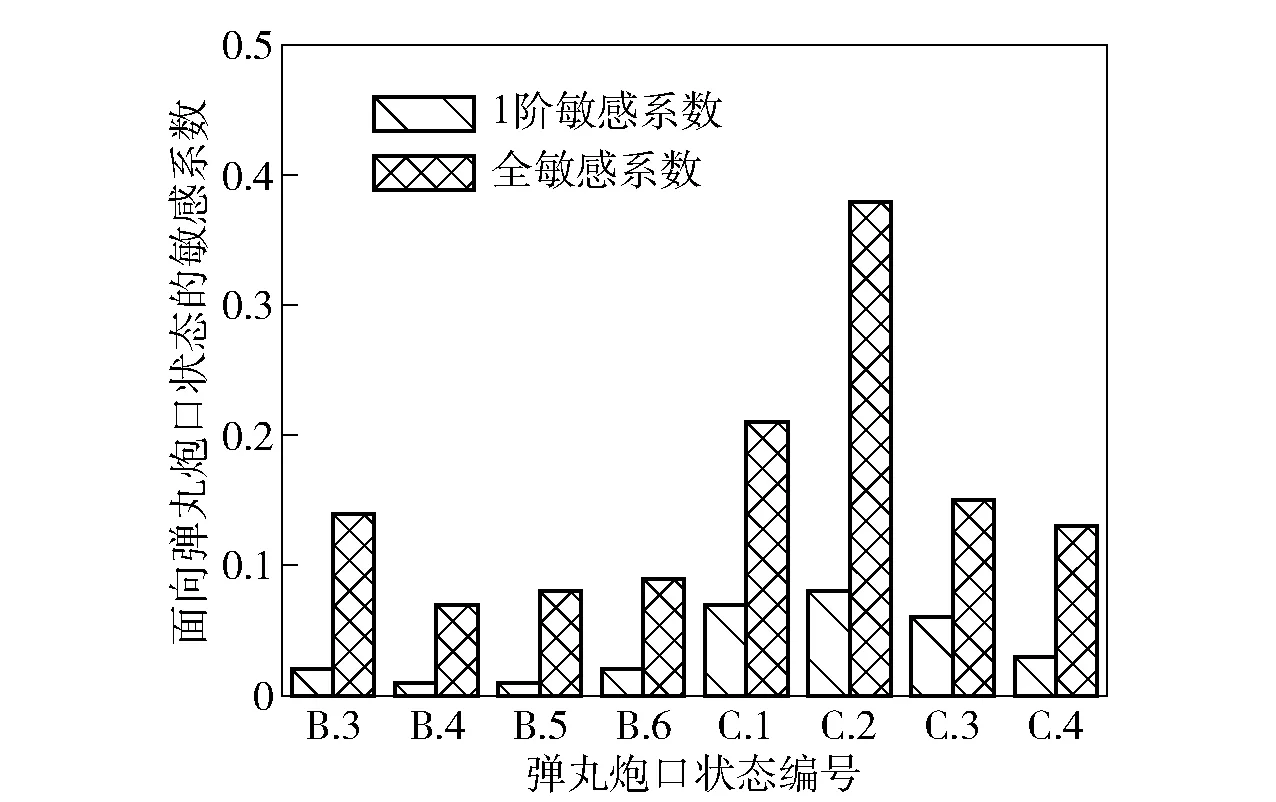
图12 结构参数敏感系数Fig.12 Sensitivity coefficients of structural parameters

为了进一步揭示自行火炮结构参数变化对最大射程条件下弹丸炮口状态的敏感规律，按表2所示分类分别计算内弹道参数、火炮整体结构参数和底盘结构参数3个变量组相对弹丸炮口状态的全敏感系数(结果如图13所示)。

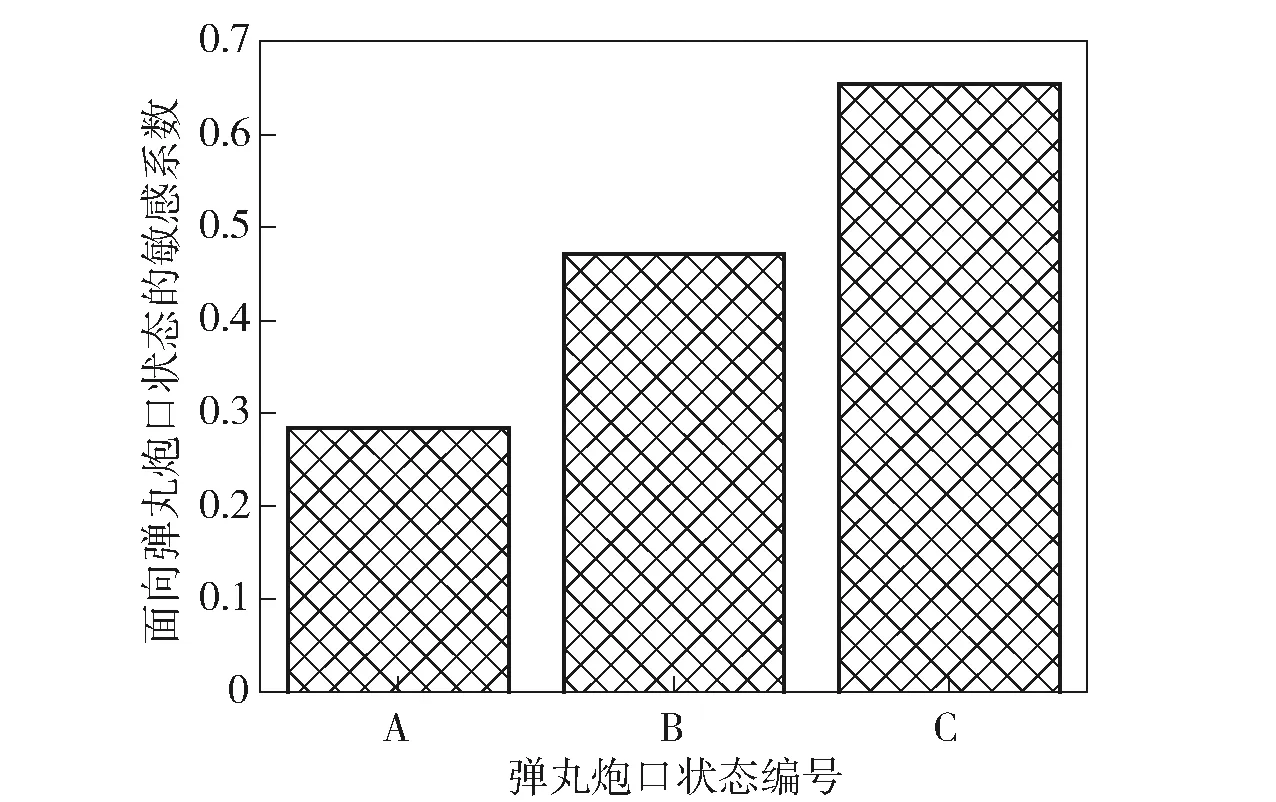
图13 变量组敏感系数Fig.13 Sensitivity coefficients of variable sets

由图13可知：内弹道参数、火炮整体结构参数和底盘结构参数3个变量组的全敏感系数均小于其包含所有变量的全敏感系数之和；内弹道参数、火炮整体结构参数和底盘结构参数3个变量组的全敏感系数之和大于1. 产生这种现象的原因是：自行火炮是一个复杂综合性系统，不同变量组的全敏感系数间存在重叠的部分。这也进一步说明内弹道参数、火炮整体结构参数和底盘结构参数并不是单独作用于弹丸炮口状态，而是通过相互间的协同作用于弹丸炮口状态。

鉴于上述现象，如果要了解自行火炮若干个变量同时对弹丸炮口状态的敏感程度，最好将这些变量组合成一个变量组，然后计算这个变量组对弹丸炮口状态的敏感系数。这样能够更加准确地评估该变量组对弹丸炮口状态的敏感程度。借助变量组敏感系数的计算，可以更加准确地进行自行火炮不同部件间的敏感程度比较，为设计人员提供更加准确的灵敏度数据。

4 结果验证

文献[11]提供的全局灵敏度分析方法计算量较大，但是结果是正确的。为了实现对上述方法和相关分析结果的验证，利用文献[11]提供的全局灵敏度分析方法，进行同等条件下弹丸炮口状态的全局灵敏度分析(详细结果如表4和表5所示)。对比表4和表5所示结果和图9～图13所示结果后，发现：根据两种不同的计算方法，弹丸炮口状态各特征量的敏感系数是一致的；自行火炮各结构参数的敏感系数是一致的。这说明本文提供的全局灵敏度方法和相关灵敏度分析结果是可信的。同时估计表4和表5所示结果，文献[15]提供的方法总共用了98 000组数据，本文提供的方法总共用了8 700组数据；估计表6所示结果，文献[15]提供的方法总共用了70 000组数据，本文提供的方法总共用了6 500组数据。所以本文提供的方法提高了全局灵敏度分析方法的计算效率。

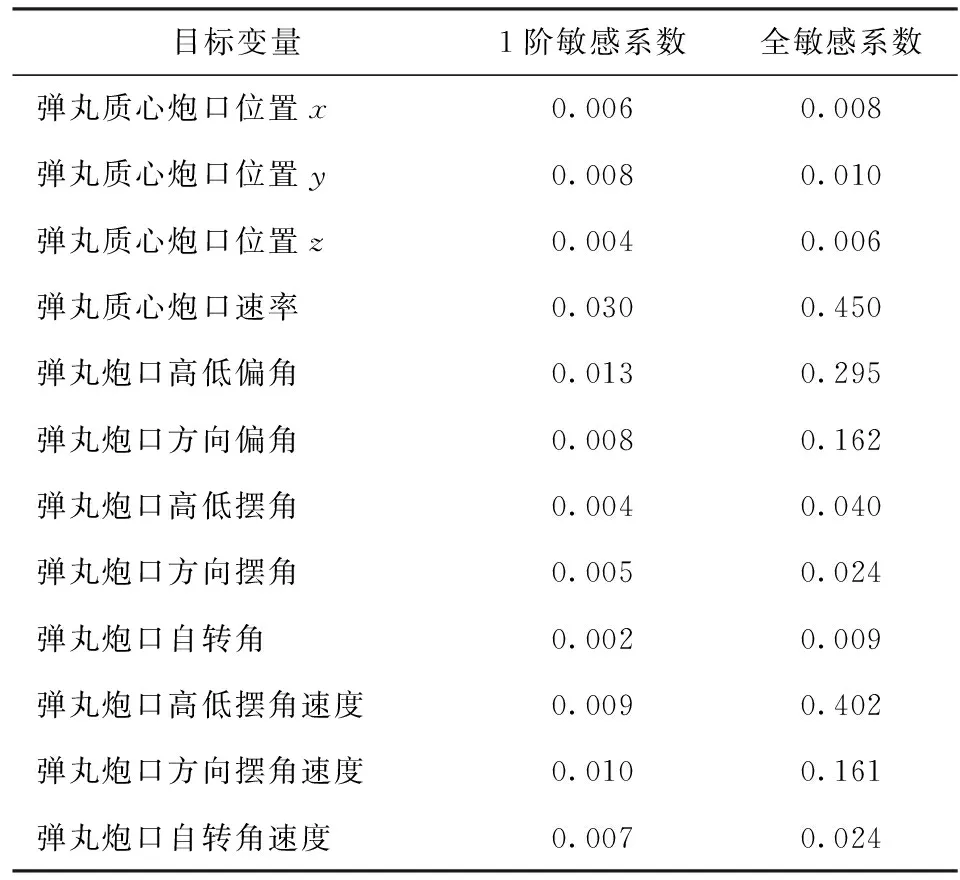
表4 面向弹丸落点纵向位移的敏感系数

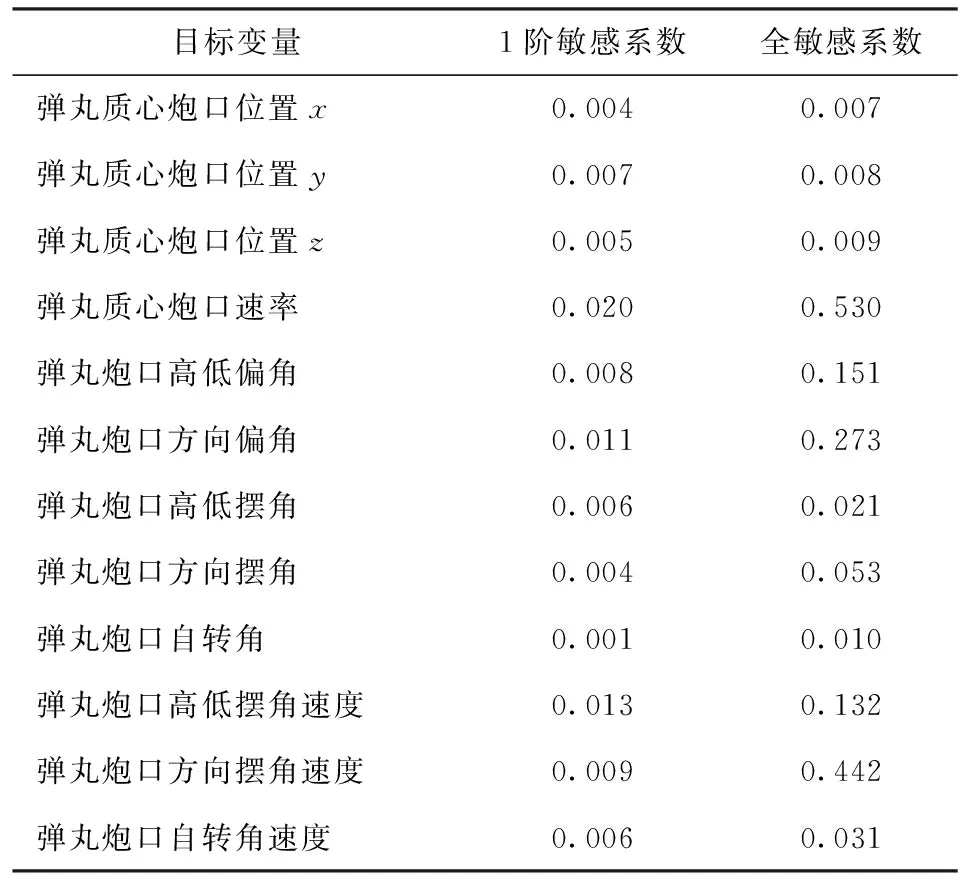
表5 面向弹丸落点横向位移的敏感系数

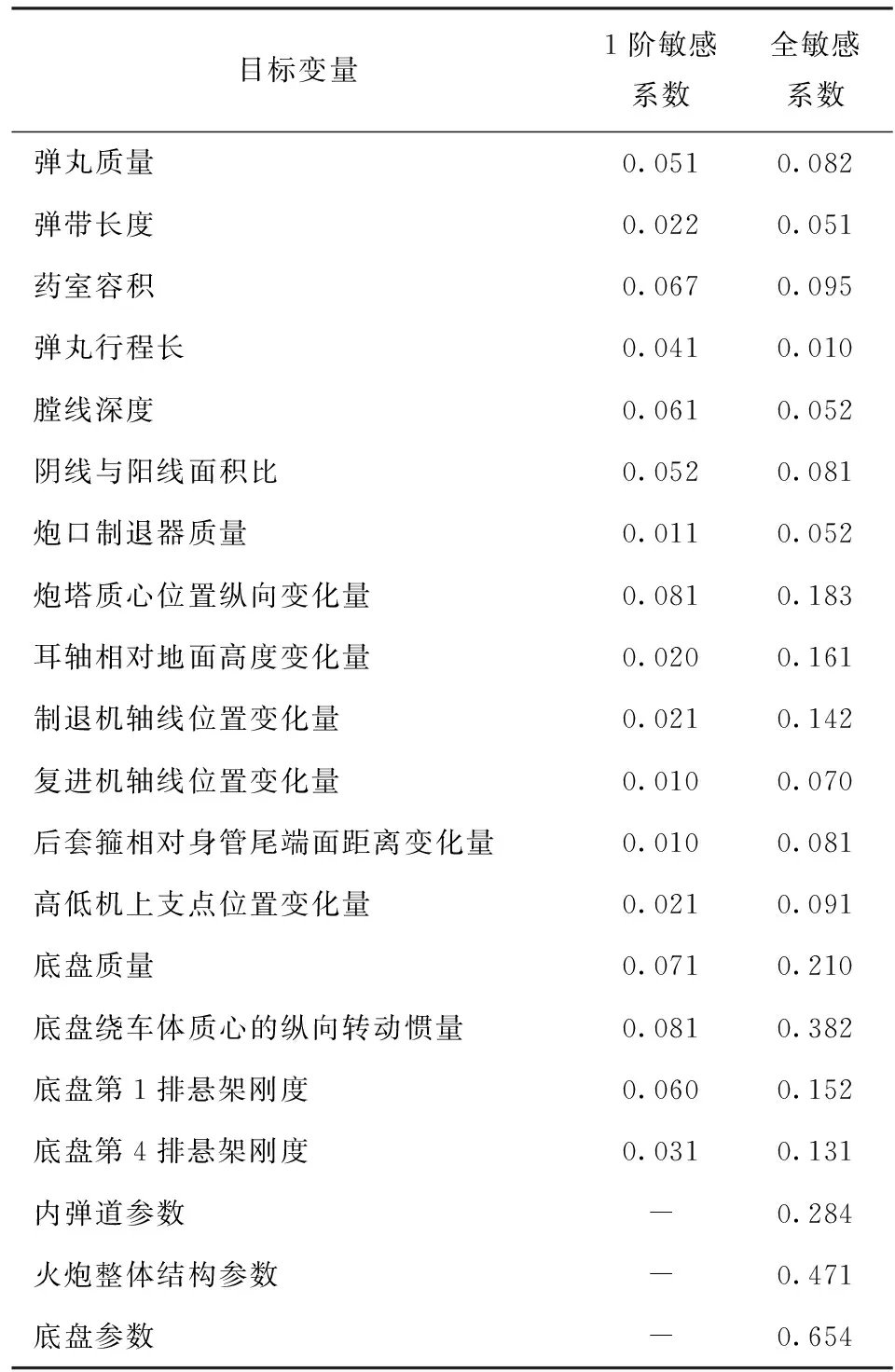
表6 面向弹丸炮口状态的敏感系数

5 结论

为了研究给定分布条件下自行火炮结构参数对弹丸炮口状态的敏感程度，本文建立了某自行火炮整体发射动力学模型，提出一种全局灵敏度分析方法，并应用上述模型和方法进行了实例分析。具体贡献和结论如下：

1) 建立了能够同时考虑弹丸膛内运动和车体振动的自行火炮整体发射动力学模型。

2) 提出了一种全局灵敏度分析方法。该方法证明了连续相关实向量可以用任意连续独立实向量表示；输入变量为任意连续独立实变量条件下，通过对独立变量组1阶敏感系数和全敏感系数的估计，实现了相关变量组1阶敏感系数和全敏感系数的估计。

3) 根据上述方法，进行了最大射程条件下，面向弹丸炮口状态的某自行火炮结构数全局灵敏度分析。结果显示：底盘纵向转动惯量是影响最大射程条件下某自行火炮弹丸炮口状态的最大因素。

参考文献(References)

[1] 陈光宋. 弹炮耦合系统动力学及关键参数识别研究[D]. 南京：南京理工大学, 2016.

CHEN G S. The study on the dynamics of the projectile-barrel coupled system and the corresponding key parameters[D]. Nanjing: Nanjing University of Science and Technology, 2016. (in Chinese)

[2] 罗中峰,管小荣,徐亚栋,等.某火炮弹丸在炮口状态的动态灵敏度分析[J].兵工学报,2017,38(12):2328-2336.

LUO Z F, GUAN X R, XU Y D, et al. Analyses of parameter sensitivity for position and attitude of projectile at muzzle[J]. Acta Armamentrii, 2017, 38(12):2328-2336. (in Chinese)

[3] 王晓锋,姜兴渭. 有限段法在高炮发射多体系统动力学分析中的应用[J]. 南京理工大学学报,2001,25(1):25-27.

WANG X F, JIANG X W. Application of finite segment method to dynamic analysis of antiaircraft gun launch[J]. Journal of Nanjing University of Science and Technology, 2001,25(1):25-27. (in Chinese)

[4] 刘飞飞,芮筱亭,于海龙, 等. 自行火炮行进间发射动力学研究[J]. 振动工程学报, 2016,29(3):380-385.

LIU F F, RUI X T, YU H L, et al. Study on launch dynamics of the self-propelled artillery marching fire [J]. Journal of Vibration Engineering, 2016,29(3):380-385. (in Chinese)

[5] 景鹏渊,顾克秋. 后坐体结构参量对弹丸起始扰动的影响[J]. 兵器装备工程学报, 2017,38(2):53-56.

JING P Y，GU K Q．Impact of structure parameter of recoiling parts on the initial projectile disturbance[J]．Journal of Ordnance Equipment Engineering，2017，38(2):53-56. (in Chinese)

[6] SALTELLI A. Making best use of model evaluations to compute sensitivity indices[J]. Computer Physics Communications, 2002, 145(2): 280-297.

[7] SALTELLI A, TARANTOLA S. On the relative importance of input factor in mathematical models[J]. Statistical Association, 2002, 97(459): 8-30.

[8] KUCHERENKO S, TARANTOLA S, ANNONI P. Estimation of global sensitivity indices for models with dependent variables[J]. Computer Physics Communications, 2012, 183(4): 937-946.

[9] XU C G, GERTNER G Z. Uncertainty and sensitivity analysis for models with correlated parameters[J]. Reliability Engineering & System Safety, 2008, 93(10): 1563-1573.

[10] LI G Y, RABITZ H, YELVINGTON P E,et al. Global sensitivity analysis for systems with independent and/or correlated inputs[J]. Physical Chemistry A, 2010, 114(19): 6022-6032.

[11] MARA T A, TARANTOLA S, ANNONI P. Non-parametric methods for global sensitivity analysis of model output with dependent inputs [J]. Environmental Modelling & Software, 2015,72:173-183.

[12] TARANTOLA S, MARA T A. Variance-based sensitivity indices of computer models with dependent inputs: the Fourier amplitude sensitivity test[J]. International Journal for Uncertainty Quantification, 2017,7(6):511-523.

[13] DECARLO E C, MAHADEVAN S, SMARSLOK B P. Efficient global sensitivity analysis with correlated variables[J]. Structural and Multidisciplinary Optimization, 2018, 58(6): 2325-2340.

[14] ZHOU Y C, LU Z Z, XIAO S A, et al. Distance correlation-based method for global sensitivity analysis of models with dependent inputs[J]. Structural and Multidisciplinary Optimization, 2019,60(3):1189-1207.

[15] 韩子鹏. 弹箭外弹道学[M], 北京:北京理工大学出版社,2014.

HAN Z P. Exterior ballistics of projectiles and rockets[M]. Beijing: Beijing Institute of Technology Press,2014. (in Chinese)

[16] LANKARANI H M, NIKRAVESH P E. A contact force model with hysteresis damping for impact analysis of multibody system[J]. Journal of Mechanical Design, 1990, 112(3): 369 -376.

[17] WONG J Y, REECE A R. Prediction of rigid wheel performance based on the analysis of soil-wheel stresses part I. performance of driven rigid wheels[J]. Journal of Terramechanics, 1967,4(1):81-98.

[18] 罗中峰. 某特种机械的稳健设计方法研究[D]. 南京：南京理工大学,2020.

LUO Z F.Research on robustness design methods of a special machinery [D]. Nanjing: Nanjing University of Science and Technology, 2020. (in Chinese)

[19] ROSENBLATT M. Remarks on a multivariate transformation [J]. The Annals of Mathematical Statistics, 1952, 43: 470-472.

[20] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京: 高等教育出版社, 2001.

SHENG Z, XIE S Q, PAN C Y.Probability theory and mathematical statistics[M]. Beijing: Higher Education Press, 2001. (in Chinese)

[21] METROPOLIS N, ULAM S. The Monte Carlo method[J]. Journal of the American Statistical Association, 1949, 44(247):335-341.