爆炸冲击波作用下黑索今基含铝炸药的冲击点火反应速率模型

王虹富， 白帆， 刘彦,2， 段卓平， 黄风雷

(1.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081; 2.北京理工大学重庆创新中心， 重庆 401120)

0 引言

铝作为一种易燃高能材料，经常被添加到炸药中以改善其性能[1-5]。铝粉的加入可以提高爆温，延长炸药的做功时间，增强爆轰的损伤效应[6-8]，而大部分铝粉在爆轰过程中的惰性导致了含铝炸药的爆速和爆压较低[8-9]。含铝炸药是典型的非理想炸药，目前铝粉与爆轰产物的反应机理是国内外学者的研究重点，但对点火阶段时铝粉与炸药分解产物的反应模型研究较少[2,4,7,10-11]。与其他炸药相比，黑索今(RDX)基含铝炸药的冲击波超压衰减速度较缓，其优异的性能和应用价值引起了广泛关注[12-15]。RDX基含铝炸药在使用、运输和储存过程中，需要较高的冲击稳定性和较低的冲击感度。对于特定的含铝炸药配方，铝的反应速率和反应活性主要取决于铝颗粒的尺寸大小[16-17]。因此，关于铝粉尺寸对含铝炸药冲击点火影响的研究具有重要意义，可以为评价RDX基含铝炸药的安全性和可靠性提供依据；同时提出RDX基含铝炸药冲击点火模型，以计算不同铝粉粒径炸药在点火阶段铝的反应度和反应速率，对研究铝粉粒径与炸药冲击点火的关系具有指导作用。

冲击感度是炸药的一个重要特性，对炸药受到外部冲击作用时的安全性评价具有重要意义。要研究冲击感度，首先必须分析炸药的点火机理，对凝聚炸药冲击点火机理的研究可以概括为宏观和细观两个方面。一方面，目前众多学者已经提出了很多宏观经验模型，比如Forest Fire模型[18]， Johnson-Tang-Forest(JTF)模型[19]、HVRB模型[20]和Lee-Tarver点火增长模型[21]，其中：Lee-Tarver点火增长模型[21]提出了一个包含物理和化学反应的冲击起爆过程的广义描述，广泛应用于冲击点火问题的研究。另一方面，Kim[22]、温丽晶等[23]、Duan等[24]、Liu等[25]提出了各种细观反应速率模型，其中：基于Kim[22]提出的球壳塌缩模型，文献[23-25]考虑了粘结剂的作用，建立了炸药热点形成的双球壳塌缩模型，该模型成功地描述了粘结剂含量和强度、炸药颗粒尺寸和孔隙率等参量对炸药冲击点火的影响；文献[25]建立了多组分高聚物粘结炸药(PBX)冲击起爆的细观反应速率模型。

近年来，在国内外学者对含铝炸药冲击起爆的深入研究中，大多采用I&G反应速率模型并将含铝炸药视为均匀介质，而不考虑铝反应。通过数值模拟和与之对应的爆轰实验，Lu等[26-27]建立了PBXN-115和PBXN-109的Lee-Tarver模型参数。Bohoon[28]考虑RDX基含铝炸药中铝粉的反应，对Lee-Taver模型进行改进，得到了新的反应速率模型，能够描述RDX含铝炸药的冲击起爆过程，克服了三项式参数过多的局限。Cao等[29]研究了RDX/2，4-二硝基苯甲醚(DNAN)/铝炸药的冲击起爆特性，利用实验结果给出了该含铝炸药的I&G模型参数，实验和模拟结果表明随着铝粉颗粒的减小，含铝炸药的冲击感度增加。

目前，含铝炸药的爆轰机理主要是Cook等[30]提出的二次反应理论，即认为铝粉在波阵面上一般不参与反应，铝粉与爆轰产物的反应发生在声界面之后，产生的能量不能用于支持爆轰波的传播。目前很少有在反应速率模型中引入铝组分的反应。然而，另外一些研究人员认为在冲击转爆轰的过程中，铝粉可以在热点形成阶段发生反应，为爆轰的传播提供能量[31]。Baker等[32]在Jones-Wilkins-Lee(JWL)状态方程中增加了一项，用于说明含铝炸药中的铝反应，以描述爆轰产物的膨胀。Gogulya等[33-34]的研究表明，纳米级铝颗粒的加入使奥克托今(HMX)的临界点火压力降低了33%，他们认为纳米级铝粉的高比表面积在热点形成过程中促进了铝与高能炸药分解产物的相互作用。

为研究铝粉尺寸对RDX基含铝炸药(按质量计64%RDX，20%铝，16%粘结剂)冲击点火和随后爆轰增长过程的影响，基于锰铜压阻传感器测压技术，对200 μm RDX粒径但混入5 μm、16 μm、40 μm和100 μm4种不同铝粉粒径的炸药配方进行了含铝炸药冲击起爆一维拉格朗日实验。本次研究测量了实验中压力信号的变化历程，利用I&G模型和考虑了铝粉在CJ面前参与反应的细观反应速率模型计算了在冲击起爆过程中RDX基含铝炸药在CJ面前的压力增长过程；在模拟计算过程中，将该细观模型嵌入LS-DYNA中进行相应的模拟计算，以精确模拟冲击点火起爆过程；同时利用实验结果比较了不同铝粉粒径对炸药冲击感度的影响。

1 冲击点火起爆实验研究

为分析铝粉尺寸对RDX基含铝炸药(64%RDX、20%铝、16%粘结剂)冲击起爆过程的影响机制，本文对除了铝粉尺寸(5 μm、16 μm、40 μm、100 μm)不同以外其他特性参数完全相同的4种RDX含铝炸药进行了冲击起爆实验研究。此外铝粉粒径为16 μm的炸药配方与文献[19]中的PBXN109基本相同。冲击起爆一维拉格朗日实验分析测试系统如图1所示，实验原理为雷管引爆炸药平面波透镜，同时导通触发探针,触发脉冲恒流源开始给锰铜压阻传感器供电，炸药透镜产生的平面爆轰波起爆梯恩梯(TNT)传爆药柱，进而产生更强的爆轰波经铝隔板和空气隙衰减后得到的平面冲击波传入至待测试的含铝炸药中,实现对炸药的冲击加载,埋在炸药中4 个不同拉格朗日位置的锰铜压阻传感器测得当地压力信号,并通过示波器记录。

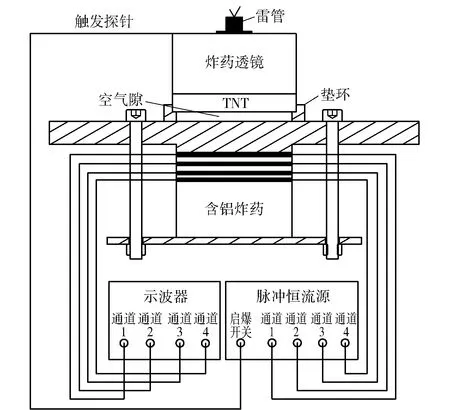
图1 RDX基含铝熔铸炸药冲击起爆实验系统Fig.1 Experimental setup for shock initiation of RDX aluminized melt-cast explosives

图1中的实验装置由加载系统、信号采集系统和RDX基含铝炸药样品组成。加载系统采用炸药平面透镜爆轰加载及空气与隔板综合衰减技术，由雷管、φ50 mm的平面波发生器、φ60 mm×20 mm的TNT传爆药柱、2 mm厚的空气隙和13 mm厚的铝隔板构成；待测炸药样品直径为40 mm，3块厚3 mm的薄片炸药样品和1块厚25 mm的炸药样品相叠，并嵌入4个锰铜压阻传感器，通过变化薄片炸药的厚度来调整所需测试的拉格朗日位置。在实验中，理论上可增加炸药厚度和传感器数量来得到全面详细的数据；而实际实验时，受传感器安放过多，后端传感器容易被干扰、炸药冲击转爆轰以及爆轰传播易被中断等因素的制约，一次实验通常测量4个位置的压力比较合适。首先需要在0 mm处设置拉格朗日点，测量各组实验的入射压力并判断是否相同，确保实验结果的可对比性；根据本次实验条件中的各含铝炸药到爆轰距离的范围：4～5 mm，需要在到爆轰距离前设置一个拉格朗日点测量和研究炸药内部冲击转爆轰的压力成长过程，因此在3 mm处设置拉格朗日点；同样需要在到爆轰距离后并且充分爆轰前(压力峰值略低于充分爆轰时炸药内部的爆压)设置拉格朗日点，因此在6 mm处设置拉格朗日点；然后需要在含铝炸药内充分爆轰时的位置设置拉格朗日点，因此在9 mm处设置拉格朗日点。信号采集系统由示波器、脉冲恒流源、触发探针和锰铜压阻传感器组成。使用的锰铜压阻传感器为H型，传感器电阻约为2 Ω，同时为维持爆轰压力测量时间并防止炸药样品反应后的导电性所造成传感器短路，每个传感器两面用聚四氟乙烯薄膜包覆，第一个位置的薄膜厚度为0.2 mm，其余3个位置的薄膜厚度为0.1 mm，使用真空硅脂封装。脉冲恒流源由北京理工大学爆炸科学与技术国家重点实验室研制，一台仪器包含4个通道，可以同步输出4路恒流，同时给4个压阻传感器供电，实验时设置脉宽为200 μs；示波器选取Tektronix4034数字荧光示波器，带宽为350 MHz，最高采样速率为2.5 GS/s，实验时设置采样速率为500 MS/s，最大记录长度10 M采样点，足够满足测试系统的要求。

本文中的冲击起爆实验均在同一加载装置下进行，其输出的加载压力约为6.4 GPa左右，保持每发实验的输入条件一致，对4种铝粉尺寸的含铝炸药冲击起爆过程进行测试。实验中的RDX基含铝炸药特性参数如表1所示。为区分实验结果之间的有意义差别和随机误差；同时确定这些有意义差异是铝粉粒径本身造成的，而并非由于实验装置、测量误差、样品制备精密度(或缺乏精密度)等引起，需要对实验结果进行预期误差范围分析和不确定性分析。4种RDX基含铝炸药各进行两次实验，选取实验结果中的前导冲击波到达时间(冲击波压力达到5 GPa时所对应的时间)、压力峰值时间和压力峰值(在3 mm拉格朗日位置处出现两个压力峰值)等参量，如图2所示；同时实验的预期误差范围分析如图3～图5所示，并且在图3和图4中，每种含铝炸药的第1次实验结果以虚折线表示，第2次实验结果以孤立的几何图形表示。对于这4种RDX基含铝炸药，上述3个参量在各拉格朗日位置处的最大预期误差范围如表2所示。同时在本文接下来的研究中，通过对每种含铝炸药的两次实验结果进行平均处理来获得实验数据以减少随机误差。

表1 实验中RDX基含铝炸药的特性参数

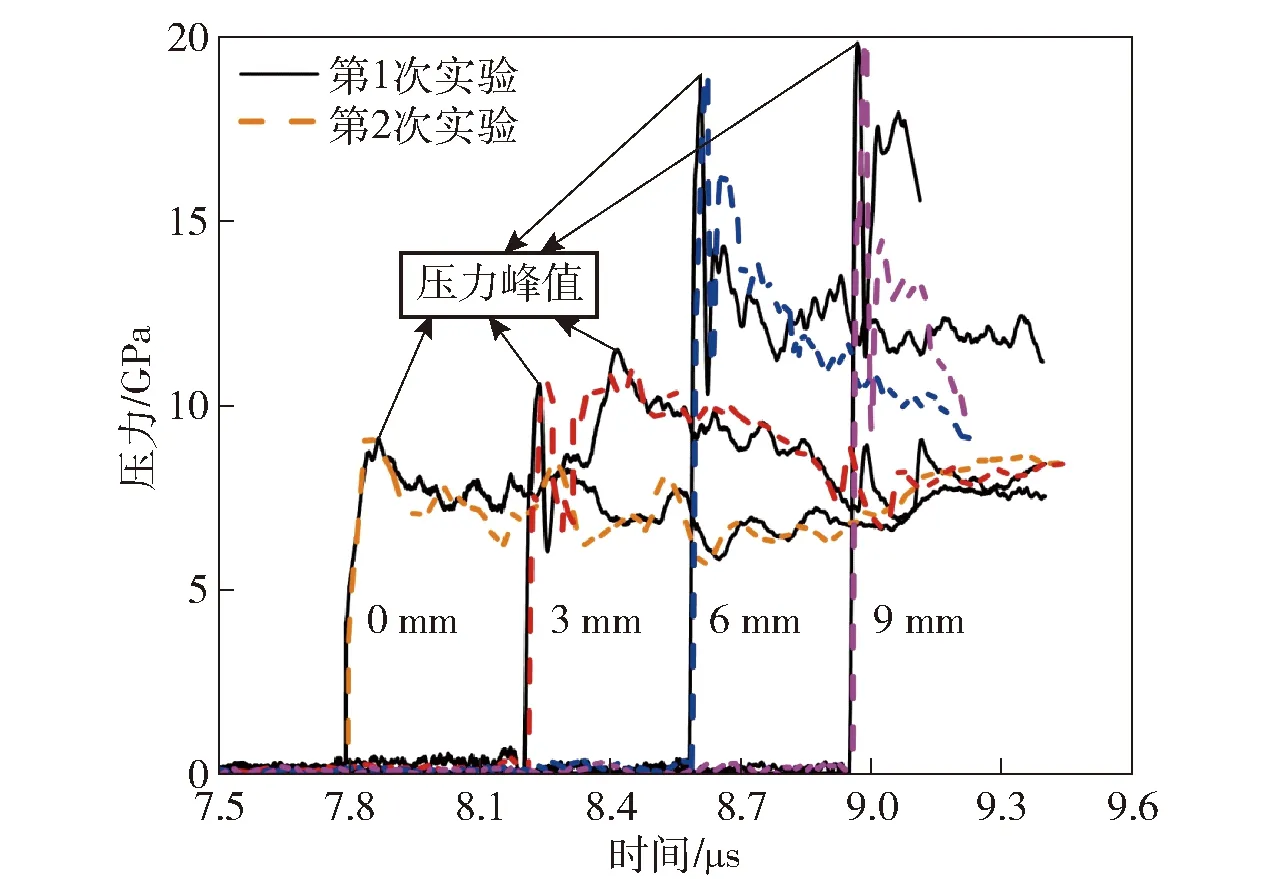
图2 16 μm铝粒径RDX基含铝炸药两次冲击起爆实验的压力曲线Fig.2 Two impact initiation pressure curves of RDX-based aluminized explosives with 16 μm aluminum particle size

图3 4种铝粉粒径RDX基含铝炸药冲击波到达时间的实验曲线Fig.3 Experimental curves of shock-wave arrival times of four kinds of RDX-based aluminized explosives

图4 4种铝粉粒径RDX基含铝炸药压力峰值时间的实验曲线Fig.4 Experimental curves of peak-pressure times of four kinds of RDX-based aluminized explosives

图5 4种铝粉粒径RDX基含铝炸药压力峰值的实验曲线Fig.5 Experimental curves of peak pressures of four kinds of RDX-based aluminized explosives

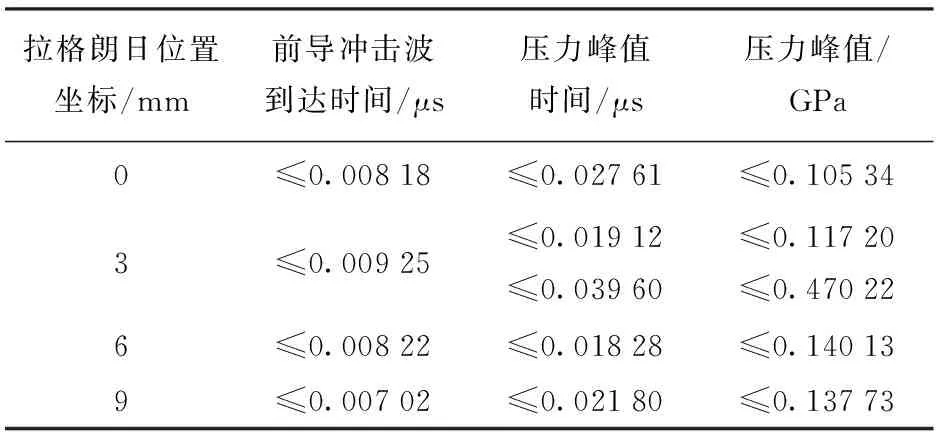
表2 各拉格朗日位置实验数据的最大预期误差范围

在同一加载压力下，4种铝粉粒径RDX基含铝炸药在对应的0 mm、3 mm、6 mm、9 mm拉格朗日位置上的冲击起爆压力曲线如图6所示，从中可看出，平面爆轰波对含铝炸药样品的初始冲击时间为7.787 μs. 根据实验数据发现5 μm铝粉粒径RDX基含铝炸药在3 mm、6 mm和9 mm测量位置的前导冲击波到达时间和压力峰值时间早于其他3种含铝炸药，并且前导冲击波的压力峰值较高，上述参量的具体差值如表3～表5所示。相比0 mm拉格朗日位置，在3 mm位置处的前导冲击波过后出现明显的压力增长过程。Grebenkin[35]基于热点概念提出非均质高能炸药的宏观化学反应动力学受到3种因素的控制：细观热点密度、热点燃烧波传播速度和燃烧拓扑。因此上述现象可能是由于不同加载压力下产生的热点数量和尺寸不同，导致前导冲击波过后反应的程度不同，从而造成压力变化趋势不同。

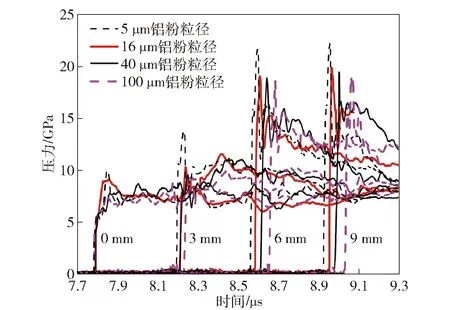
图6 4种铝粉粒径RDX基含铝炸药在各拉格朗日位置上的冲击起爆压力曲线Fig.6 Impact initiation pressure curves of RDX-based aluminized explosives with four kinds of aluminum particle sizes

根据前导冲击波压力峰值和峰值时间，拟合得到4种铝粉粒径RDX基含铝炸药的前导冲击波阵面压力历程曲线如图7所示，从中可以看出含铝炸药的爆轰时间和到爆轰距离可以衡量炸药的冲击感度。本文选取炸药内的爆轰压力达到15 GPa时所对应的时间为爆轰时间；受到给定幅值和脉冲宽度的冲击后，在炸药内形成定常爆轰所需的距离为到爆轰距离。根据图7可知，5 μm、16 μm、40 μm和100 μm铝粉粒径RDX基含铝炸药的爆轰时间和到爆轰距离分别为8.320 73 μs、8.430 52 μs、8.453 38 μs、8.486 56 μs和4.020 11 mm、4.744 41 mm、4.787 82 mm、4.813 86 mm，上述分析表明较小颗粒尺寸的铝组分可以提高含铝炸药的反应速率和冲击感度。图8为相对于0 mm拉格朗日位置的冲击波到达时间，各含铝炸药冲击起爆前导冲击波到达不同位置的时间分布图，图9为各含铝炸药冲击起爆前导冲击波阵面到达不同位置时的压力峰值比较图(横坐标为：相对于0 mm拉格朗日位置的冲击波压力峰值时间，各位置处的前导冲击波压力峰值时间)，对4种铝粉粒径RDX基含铝炸药中前导冲击波的变化情况进行了比较。由图8和图9可以看出：铝粉颗粒度的增加，前导冲击波到达同一位置的时间变长，速度增长变慢；前导冲击波阵面压力增长变缓，到爆轰时间变长，炸药感度降低。

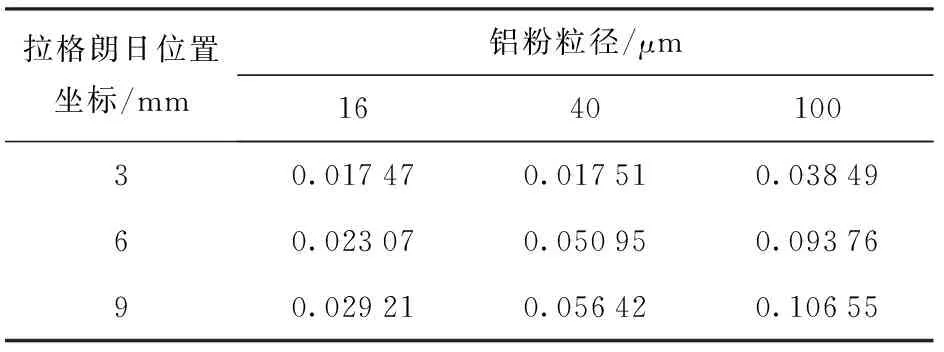
表3 5 μm铝粉粒径RDX基含铝炸药在各拉格朗日位置上的前导冲击波到达时间与其他3种铝粉粒径RDX基含铝炸药配方对应的差值

表4 5 μm铝粉粒径RDX基含铝炸药在各拉格朗日位置上的压力峰值时间与其他3种铝粉粒径RDX基含铝炸药配方对应的差值

表5 5 μm铝粉粒径RDX基含铝炸药在各拉格朗日位置上的压力峰值与其他3种铝粉粒径RDX基含铝炸药配方对应的差值

图7 前导冲击波压力历史的拟合曲线Fig.7 Fitting curves of leading shock-wave pressure histories

图8 前导冲击波到达时间分布图Fig.8 Distribution of leading shock wave arrival times

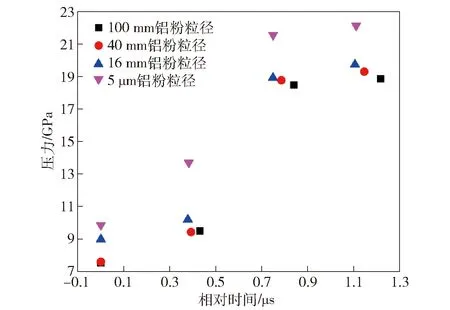
图9 前导冲击波阵面压力分布图Fig.9 Comparison of leading shock wave pressures

2 含铝炸药的冲击起爆细观反应速率模型

本文采用两种不同的反应速率方程模拟含铝炸药的冲击起爆实验，其中4种铝粉粒径RDX基含铝炸药除铝粉尺寸不同以外其他特性参数完全相同，此外铝粉尺寸为16 μm的炸药配方与PBXN109基本相同[19]。当含铝炸药中的铝粉粒径在一定范围内且其他各组分及配比相同时，炸药中铝粉粒径主要影响反应速率方程，铝粉粒径的变化对未反应炸药和爆轰产物的状态方程影响很小，因此本文忽略了这一影响，4种铝粉粒径RDX基含铝炸药均采用PBXN-109的状态方程参数。

2.1 反应的状态方程

两种反应速率模型都需使用两个JWL状态方程，一个状态方程用于未反应炸药，另一个状态方程用于反应产物，其形式为

(1)

式中：p为爆轰产物压力；V为爆轰产物相对体积；T为温度；ω为Grüneisen系数；cv为热容；A、B、R1和R2为经验参数。JWL状态方程的参数和I&G反应速率模型的参数在表6中已给出，文中的RDX含铝炸药特性参数如表1所示。

2.2 含铝炸药的I&G 反应速率模型

凝聚非均质炸药冲击起爆的点火增长反应速率模型通常采用Lee-Tarver的点火增长3项式，其形式为

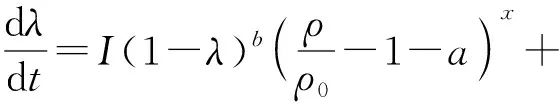
(2)

式中：λ为炸药反应度，dλ/dt为反应速率；ρ0为炸药初始密度；ρ为炸药密度；p为压力；I、a、b、x、G1、G2、c、d、y、f、h和z为常数。其中：a为临界压缩度，用来限定点火界限，当压缩度小于a时炸药不点火；或者说，当冲击波足够强(具有一定压力)，使炸药达到一定压缩度时才能点火，从而为炸药起爆规定了一个必要条件。对于ZND结构假设的爆轰波，公式的第1项代表部分炸药在冲击压缩下被点火，其点火过程没有明确表明，可能是孔洞塌缩、绝热剪切带等点火机制；第2项代表炸药快速反应产生CO2、H2O、N2和CO等气体产物；第3项代表在主要反应后相对缓慢的扩散控制反应。反应速率方程在计算过程中，须设定反应度λ的几个极值λI，max、λG1，max、λG2，min，以便使3项中的每一项在合适的λ值时开始或截断：当λ>λI，max时，点火项取为0；当λ>λG1，max时，燃烧项取为0；当λ<λG2，min时，快反应项取为0. 通过对性质确定(如孔隙率和粒径)的某特定炸药进行经验拟合得到Lee-Tarver模型的参数。炸药微结构特性的任何变化都可能需要一组不同的参数。PBXN-109的I&G反应流模型参数[27]如表6所示。

表6 PBXN-109的I&G反应速率模型相关参数

2.3 含铝炸药的冲击点火细观反应速率模型

根据文献[36]可知，PBXN-109中的增塑剂DOA对RDX的不敏感性有较大影响，2.0～3.5 J的撞击能量差异对应变化10%～20%的不敏感性，不可忽视。同时如扫描电镜图像所示[37]，PBXN-109中的不良空隙导致了相对较高的冲击敏感性。在冲击起爆过程中，这些空隙被绝热压缩，导致生成热的快速产生，这足以引发炸药的热分解、爆炸等反应。

基于Liu等阐述的二元混合PBX炸药孔隙塌缩热点模型[25]，本文通过将铝粉简化成单独的炸药主要组分之一进行分析，并通过合理假设提出了含铝炸药的孔隙塌缩热点模型。假定的含铝炸药细观结构图如图10所示。

图10 假定的含铝炸药细观结构图Fig.10 Assumed microstructure of aluminized explosive

为了便于数学描述，又不失热点的基本特征，同时考虑到两种组分不同的颗粒度，将图10所示的结构简化为图11所示的不规则双球壳模型，即二元混合炸药胞元模型[25]，并且假设炸药组分和粘结剂均为弹黏塑性材料。图11中：下标1和2用于区分两种不同组分(RDX和铝)；ro，1、ro，2为双球壳的外半径，代表炸药中两种组分颗粒各自的平均半径，ri,1、ri,2为双球壳的内半径，代表炸药中孔隙半径；rm,1、rm,2为RDX(或铝)与粘结剂交界面半径；p0为双球壳外半径处所受的冲击波压力；pg为孔隙内气压，其初值为0 GPa.

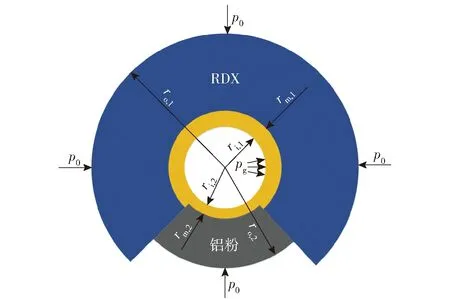
图11 胞元模型Fig.11 Cell model of an aluminized explosive

在冲击波压力作用下，图11所示的胞元模型发生弹黏塑性塌缩变形。由于冲击波压力比炸药强度大得多，并且这里孔隙塌缩热点模型本身就是热点的统计平均，因此这里忽略两种炸药组分在塌缩变形过程中相互的力学作用，并假设两种组分各自做球对称一维变形运动而互不影响，从而可以将图11所示的含铝炸药胞元模型拆分成RDX和铝两个独立的一元混合胞元模型，即弹黏塑性双球壳模型，并分别计算每个弾黏塑性双球壳在冲击波作用下塌缩变形和反应的过程，如图12所示。

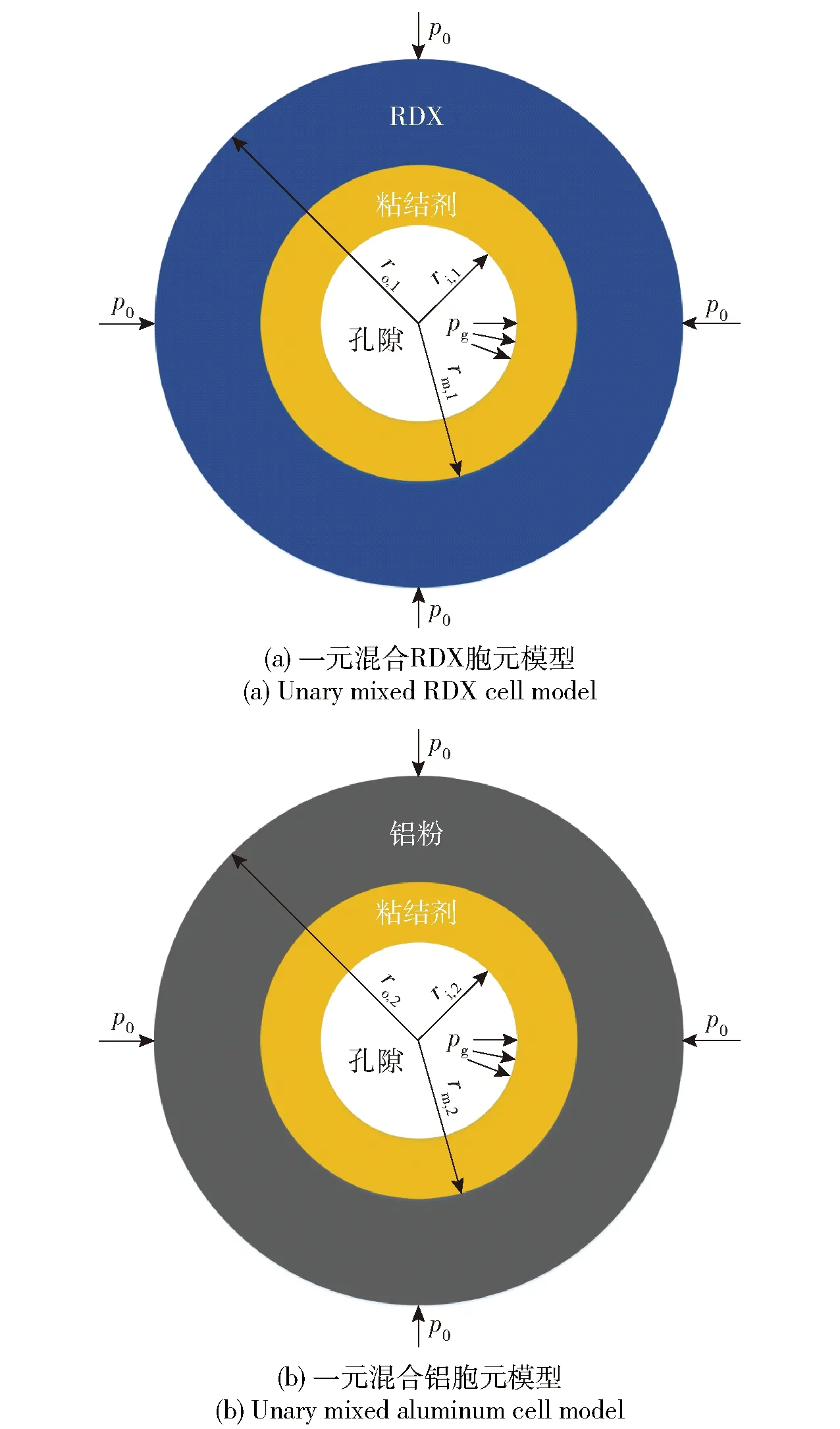
图12 两个黏弹塑性的双层球壳在冲击波作用下的独立运动Fig.12 Independent movement of two elastic/viscoplastic double-layered hollow spheres impacted by shock waves

在图12中，两个双球壳各自的半径尺寸可通过如下方法分别计算得到。炸药孔隙度τ是指炸药中孔隙体积与炸药体积的比，因此有

(3)

另外，对于给定的含铝炸药，粘结剂与炸药体积配比β是固定值，可表示为

(4)

式中：Ve,j和Vb分别是RDX、铝组分和粘结剂的体积。对于给定含铝炸药，每种组分的平均颗粒半径ro,j已知，即可根据(3)式和(4)式分别求得炸药中RDX和铝组分所对应的ri,j和rm,j.

假设球形孔洞的内、外表面开始都没有应力的作用，当外表面受到冲击波压力p0作用时，在孔洞周围产生塑性变形，RDX(或铝)被压缩，孔洞内表面温度升高，化学反应开始发生，反应产物逐渐充满孔洞，由于化学反应释放大量能量，使热点温度进一步升高，壳体外表面的冲击波压力p0和孔隙中的气体产物压力pg保持壳体的压力平衡，对这个过程的数学描述就构成了热点点火项的反应速率。在冲击压力作用下，弹黏塑性双球壳模型的塌缩过程可以进一步分解为RDX球壳(或铝球壳)和粘结剂球壳的运动，并且在RDX(或铝)和粘结剂的交界面上满足界面连续条件，模型中RDX球壳(或铝球壳)由于力学变形引起的温升[25]为

(5)

式中：下标E表示双球壳模型中RDX和铝均为弹黏塑性变形；cp,j为RDX(或铝)的定压比热；γe,j和γb为RDX(或铝)和粘结剂与黏性有关的常数；ke,j和kb为RDX(或铝)和粘结剂的剪切强度；ρj、Tj分别为RDX和铝粉的密度、局部温度；t和r分别为时间和径向空间位置。

紧随力学变形后，炸药中同时存在热传导和化学反应两个过程，这两个过程都依赖于炸药中温度的分布，而且同时又改变这个分布。因此，球壳内总的温度变化用下式描述：

(6)

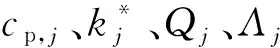
将RDX和铝粉两种组分的弹黏塑性塌缩变形过程处理为两个弹黏塑性双球壳独立运动后，利用球壳的温度分布方程(7)式和Arrhenius定律计算了每种组分的双球壳模型的局部反应速率，通过对球壳单元的局部反应速率进行积分，求解得到RDX和铝组分在点火阶段整体反应速率的具体表达式如(8)式所示：

(7)

(8)

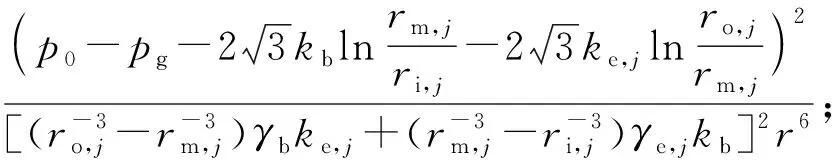
通过对RDX和铝粉两种组分整体反应速率按照体积配比进行加权即可得到整个含铝炸药的热点反应速率为

(9)

式中：φj为每种炸药组分体积分数，即

(10)

考虑到冲击波压力比炸药强度大得多，两种组分相互间的力学作用可忽略，故将图11所示的胞元模型处理成图12所示的两个弹黏塑性双球壳在冲击波作用下独立运动。两种组分是充分混合的，铝粉在点火阶段的反应度为λh,2(0≤λh,2≤1)，即铝粉不反应时为0，完全反应为1，铝粉的化学反应不是无限地进行下去，随着铝粉的氧化反应进行，生成的氧化铝就会在铝粉表面形成氧化膜，当铝粉的氧化壳达到一定厚度时，就会隔绝铝粉和周围的气体，铝粉的反应就会停止，也就是说(9)式中的λh,2=λAl(定值)时铝粉就停止了反应，则反应速率方程变成：

(11)

炸药组分的气体产物会在压力扰动的快速传播中充分混合，并很快达到压力平衡状态，因此通过炸药产物的JWL状态方程计算出孔隙压力pg.

2.4 含铝炸药的冲击起爆细观反应速率模型

采用含铝炸药的冲击起爆细观反应速率模型，其反应速率方程同样包含3项：点火项(前述已给出)如(11)式所示，主要是分析含铝炸药细观点火机制，研究炸药性质在点火阶段起的作用，考察点火过程和冲击起爆过程；低压慢反应项，假设反应为从炸药球壳的内表面以燃烧的形式向外传播，反应速率的形式与Kim[22]建立的慢反应增长项的反应速率形式相同；第3项为高压快反应项，采用Zhang[37]建立的高压反应速率方程。因为在点火项考虑铝粉和炸药的多组分作用，所以把该反应速率方程叫做含铝炸药的细观反应速率模型，形式如下：

(12)

式中：G、n、z1和y为常数，可由冲击起爆过程的实验数据确定。

对LS-DYNA进行二次开发，用FORTRAN语言把细观反应速率方程编入到LS-DYNA的接口文件dyn21b.f中，在通过编译生成细观点火增长模型，在DYNA中的状态方程(EOS)对实验中的含铝炸药冲击起爆进行数值模拟过程中，采用新生成的自定义细观反应速率模型，计算单元每一个时步长都调用新的子程序。

细观反应速率模型的未反应炸药和爆轰产物的JWL状态方程的参数与在I&G模型中使用的参数相同，不同铝粉尺寸的RDX含铝炸药细观反应速率模型参数如表7所示。

表7 黑索今基含铝炸药的冲击起爆细观反应速率模型参数

3 仿真结果与讨论

为比较含铝炸药的细观反应速率模型和I&G模型的优点与不足，在LS-DYNA中模拟了上述含铝炸药冲击起爆实验。模拟中使用在y轴方向施加约束的二维网格，网格大小为0.025 mm. 仅需对前20 mm的装药长度进行计算，因为实验在该装药长度内，已经完全包含了起爆转爆轰的过程。分别在炸药内的第0 mm、3 mm、6 mm、9 mm位置设置4个测量点，记录当地压力随时间变化曲线，同时采用实验中0 mm位置的压力时程曲线作为炸药的初始冲击边界条件。分别利用I&G模型(Lu 等[27]给出的PBXN-109参数)和细观反应速率模型(模型参数如表5所示)模拟了16 μm粒径铝粉RDX基含铝炸药的冲击起爆过程。16 μm粒径铝粉含铝炸药内的各拉格朗日位置处压力变化曲线的计算结果和实验结果对比如图13所示。

图13 I&G模型与细观反应速率模型计算的16 μm铝粉粒径含铝炸药的压力- 时间曲线与冲击起爆实验结果Fig.13 Comparison of calculated pressure time curves of I&G model and the new microscopic reaction rate model in aluminized explosive with 16 μm particle size of aluminum

由图13可知：对于上述两种反应速率模型，在0 mm拉格朗日位置处冲击加载压力相同情况下，相比细观反应速率模型，I&G模型在对应拉格朗日位置(3 mm，6 mm，9 mm)上计算的冲击波到达时间以及压力峰值与实验结果并不接近；对于I&G模型，3个位置的冲击波到达时间比实验结果更加提前，同时过高的峰值压力意味着在数值计算中不切实际的炸药反应度。上述分析表明炸药的真实反应速率远慢于给定的I&G模型所计算的速率。并且在不同PBXN-109炸药配方中的铝粉尺寸可能会存在较小的差别，尤其不同配方中所使用的粘合剂类型也可能完全不同。在模拟中仅一组I&G模型参数用于所有制药配方的PBXN-109显然是不合理的。在I&G模型中，点火增长3项式模型是唯象的经验反应速率模型，方程中并没有反映炸药自身性质的物理量，所以铝粉尺寸或粘结剂的参数等物理参量的变化并没有影响其反应速率；其参数源自实验的拟合，只能适合特定性质的炸药(如炸药颗粒尺寸、孔隙度等)，会随着炸药自身性质的改变而需要重新实验拟合。上述分析说明利用一组I&G模型参数计算某型号RDX含铝炸药冲击起爆反应进程的不适用性。

同时，本文通过细观反应速率模型计算了其他铝粉粒径(5 μm、40 μm、100 μm)的RDX基含铝炸药冲击起爆过程，模拟结果和实验数据如图14所示，从中可以发现该模型计算的压力历史和实验结果非常接近。对于100 μm、40 μm、16 μm和5 μm铝粉粒径含铝炸药(图14(a)、图14(b)、图13(a)和图14(c))，铝组分在CJ面前的反应度分别为0.80%、2.45%、3.20%和4.15%。在细观反应速率模型中，铝粉的反应方程采用Arrhenius形式，其反应速率随着颗粒半径的减小而增大，所以在球壳塌缩过程中，铝粉的反应度就会增大，而铝粉反应度的增大会使铝粉对炸药内的热点形成所贡献的能量增加，从而加速了炸药的点火，使整个炸药的反应速率增大，感度增加，缩短了冲击起爆的时间。

然而通过比较图14(a)和图14(b)发现，在图13(a)和图14(c)中的16 μm和5 μm铝粉粒径含铝炸药的模拟数据中，前导冲击波到达时间及压力峰值和实验数据相比有较大的差值，其中模拟结果的前导冲击波到达时间在对应3 mm、6 mm和9 mm拉格朗日位置上分别比实验数据分别提前了0.010 1 μs、0.042 5 μs、0.060 0 μs(16 μm铝粉粒径)和0.033 1 μs、0.062 9 μs、0.099 4 μs(5 μm铝粉粒径)；在6 mm和9 mm位置上的压力峰值比实验值分别低了3.426 62 GPa、4.013 84 GPa(16 μm铝粉粒径)和4.270 8 GPa、4.437 7 GPa(5 μm铝粉粒径)。上述分析说明该细观模型计算16 μm和5 μm铝粉粒径含铝炸药的冲击起爆存在较大误差，对于铝粉尺寸相对较小的含铝炸药(铝粉尺寸大约小于炸药颗粒尺寸的1/10)，该模型并不十分适用；并且对于RDX基含铝炸药，当铝粉粒径远小于基炸药RDX颗粒时，受铝粉尺寸的制约，在含铝炸药内部形成图10所示的细观结构图概率较低，即此类细观结构在炸药中的密度(或数量)较少，所以炸药受冲击加载时形成的热点反应机理与本文提出的两个黏弹塑性双层球壳孔隙塌缩热点模型符合度较低，下一步需对小尺寸铝粉含铝炸药的反应速率模型进行新的研究。

4 结论

1)基于锰铜压阻传感器测压技术，建立了RDX基含铝炸药冲击起爆一维拉格朗日实验分析测试系统，对5 μm、16 μm、40 μm和100 μm等不同铝粉粒径的RDX基含铝炸药冲击起爆过程进行了实验研究，结果表明：随着铝粉颗粒尺寸的增加，前导冲击波速度增长变慢，前导冲击波阵面压力增加变缓，到爆轰距离变长，炸药感度降低。

2)通过I&G模型以及Lu等[27]给出的PBXN-109模型参数，模拟了实验中16 μm铝粉粒径RDX基含铝炸药冲击起爆过程，模拟结果表明：16 μm铝粉粒径含铝炸药在0 mm位置的入射压力与实验数据相同时，冲击波到达3 mm、6 mm、9 mm测试位置的时间与实验结果均不相同，差异很大，且3个位置的压力峰值相差较大，说明利用I&G模型计算该含铝炸药的冲击起爆是不适合的。I&G模型是宏观唯象的经验反应速率模型，方程中并没有反映炸药自身性质的物理量，很难考虑影响炸药感度的某些重要因素，当铝粉颗粒尺寸或者粘结剂等不同时，起爆行为会有较大差别，使用同一组参数不能体现其反应速率的改变。

3)基于多元混合PBX炸药孔隙塌缩的热点形成机制，将铝粉简化成单独的炸药主要组分之一进行分析，根据含铝炸药中各组分的细观结构、热力学性能，化学性能以及配比相关的“混合法则”，建立了含铝炸药热点点火模型。应用该模型对RDX基含铝炸药冲击起爆过程进行数值模拟，模拟结果表明：细观反应速率模型计算40 μm和100 μm铝粉粒径含铝炸药冲击起爆压力历史和实验结果非常接近；对于100 μm、40 μm、16 μm和5 μm铝粉粒径含铝炸药，铝组分在CJ面前的反应度分别为0.80%、2.45%、3.20%和4.15%。细观模型计算5 μm和16 μm铝粉粒径含铝炸药冲击起爆数据和实验结果存在较大误差，对于铝粉尺寸约小于炸药颗粒尺寸1/10的含铝炸药，该模型并不十分理想。

参考文献(References)

[1] RUGGIRELLO K P, DESJARDIN P E, BAER M R, et al. A reaction progress variable modeling approach for non-ideal multiphase explosives[J]. International Joprnal of Multiphase Flow, 2012, 42:128-151.

[2] 陈朗, 龙新平, 冯长根, 等. 含铝炸药爆轰[M]. 北京: 国防工业出版社, 2004.

CHEN L, LONG X P, FENG C G, et al. Detonation of aluminized explosives[M]. Beijing: National Defense Industry Press, 2004.(in Chinese)

[3] KEICHER T, HAPP A, KRETSCHMER A, et al. Influence of Al/ammonium perchlorate on the performance of underwater explosives[J]. Propellants, ExplosIves, Pyrotechnics, 1999, 24(3):140-143.

[4] MANNER V W, PEMBERTON S J, GUNDERSON J A, et al. The role of aluminum in the detonation and post-detonation expansion of selected cast HMX-based explosives[J]. Propellants, Explosives, Pyrotechnics,2012, 37(2): 198-206.

[5] 张伟, 闫石, 郭学永, 等. 端羟基聚叠氮缩水甘油醚与六硝基六氮杂异伍兹烷基四元混合炸药能量释放研究[J]. 兵工学报, 2018, 39(7):1299-1307.

ZHANG W, YAN S, GUO X Y, et al. Study of the energy release of CL-20/GAP-based quaternary explosive[J]. Acta Armamentaii, 2018, 39(7):1299-1307.(in Chinese)

[6] MISHRA V S, BHAGAT A L, VADALI S R, et al. Effect of tungsten on aluminized melt cast high explosive formulations[J]. Central European Journal of Energetic Materials, 2012, 9(2):147-54.

[7] CARNEY J R, MILLER J S, GUMP J C, et al. Time-resolved optical measurements of the post-detonation combustion of aluminized explosives[J]. Review of Scientific Instruments, 2006, 77(6):063103.

[8] ARKHIPOV V I, MAKHOV M N, PEPEKIN V I, et al. Investigations into detonation of aluminized high explosives[J]. Chemical Physics Reports, 2000, 18(12):2329-2337.

[9] VADHE P P, PAWAR R B, SINHA R K, et al. Cast aluminized explosives[J]. Combustion, Explosion, and Shock Waves, 2008, 44(4):461-77.

[10] TRZCIN′SKI W A, MAIZ L. Thermobaric and enhanced blast explosives-properties and testing methods[J]. Propellants, Explosives, Pyrotechnics, 2015, 40(5): 632-644.

[11] 计冬奎, 高修柱, 肖川, 等. 含铝炸药作功能力和JWL状态方程尺寸效应研究[J]. 兵工学报, 2012, 33(5):552-555.

JI D K, GAO X Z, XIAO C, et al. Study on dimension effect of accelerating ability and JWL equation of state for aluminized explosive[J]. Acta Armamentarii, 2012, 33(5):552-555.(in Chinese)

[12] 荣吉利, 赵自通, 冯志伟, 等. 黑索今基含铝炸药水下爆炸性能的实验研究[J]. 兵工学报, 2019, 40(11):2177-2183.

RONG J L, ZHAO Z T, FENG Z W, et al. Experimental study of underwater explosion performance of RDX-based aluminized explosive [J]. Acta Armamentarii, 2019, 40(11):2177-2183.(in Chinese)

[13] TRZCINSKI W A, CUDZILO S, PASZULA J. Studies of free field and confined explosions of aluminum enriched RDX compositions[J]. Propellants, Explosives, Pyrotechnics, 2007, 32(6):502-508.

[14] TRZCINSKI W A, CUDZILO S, SZYMANCZYK L. Studies of detonation characteristics of aluminum enriched RDX compositions[J]. Propellants, Explosives, Pyrotechnics, 2007, 32(5):392-400.

[15] KUMAR A S, RAO V B, SINHA R K, et al. Evaluation of plastic bonded explosive (PBX) formulations based on RDX, aluminum, and HTPB for underwater applications[J]. Propellants, Explosives, Pyrotechnics, 2010, 35(4):359-364.

[16] BECKSTEAD M W. Correlating aluminum burning times[J]. Combustion, Explosion and Shock Waves, 2005, 41(5):533-546.

[17] BOJKO B T, DESJARDIN P E, WASHBURN E B. On modeling the diffusion to kinetically controlled burning llimits of micronsized aluminum particles[J].Combustion and Flame, 2014, 161(12):3211-3221.

[18] MADER C L. Two-dimensional homogeneous and heterogeneous wave propagation[C]∥Proceedings of the 6th Detonation Symposium. Coronado, CA, US: Office of Naval Research, 1976.

[19] JOHNSON J N, TANG P K, FOREST C A. Shock wave initiation of heterogeneous reactive solids[J]. Journal of Applied Physics, 1985, 57(9):4323-4334.

[20] STARKENBERG J. Modeling detonation propagation and failure using explosive initiation models in a conventional hydrocode[C]∥Proceedings of the 12nd Detonation Symposium. San Diego, CA,US: Office of Naval Research, 2002.

[21] LEE E L, TARVER C M. Phenomenological model of shock initiation in heterogeneous explosives[J]. Physics of Fluids, 1980, 23(12):2362-2372.

[22] KIM K. Development of a model of reaction rates in shocked multicomponent explosives[C]∥Proceedings of the 9th detonation symposium. Portland, OR, US: Office of The Chief of Naval Research, 1989.

[23] 温丽晶, 段卓平, 张震宇, 等. 刚塑性粘结剂的双球壳塌缩热点反应模型[J]. 北京理工大学学报, 2011, 31(8):883-887.

WEN L J, DUAN Z P, ZHANG Z Y, et al. Pore-collapse model of double hollow sphere with rigid-plastic binders for hot-spot ignition in shock explosives[J]. Transactions of Beijing Institute of Technology, 2011, 31(8):883-887.(in Chinese)

[24] DUAN Z P, WEN L J, LIU Y, et al. A pore collapse model for hot-spot ignition in shocked multicomponent explosives[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2010, 11(S):19-23.

[25] LIU Y R, DUAN Z P, ZHANG Z Y, et al. A mesoscopic reaction rate model for shock initiation of multi-component PBX explosives [J]. Journal of Hazardous Materials, 2016, 317:44-51.

[26] LU J P. Simulation of underwater sympathetic reaction tests for PBXW-115 (Aust)[C]∥Proceedings of the 14th International Detonation Symposium. Coeur d’Alene, ID,US: Office of Naval Research, 2010.

[27] LU J P, DANIEL M A, LOCHERT I J. Numerical and experimental studies of PBXN-109 sympathetic reaction[C]∥Proceedings of the 14th International Detonation Symposium. Coeur d’Alene, ID, US: Office of Naval Research, 2010.

[28] BOHOON K. A reactive flow model for heavily aluminized cyclotrimethylene-trinitramine[J]. Journal of Applied Physics, 2014, 116(2):023512.

[29] CAO T T, ZHOU L, ZHANG X R, et al. Shock initiation characteristics of an aluminized DNAN/RDX melt-cast explosive[J]. Journal of Energetic Materials, 2017， 35(4):1-13.

[30] COOK M A, FILLER A S, KEYES R T, et al. Aluminized explosives[J]. Journal of Physical Chemistry, 1957, 61(2): 189-196.

[31] BAI F, LIU Y, HUANG F L, et al. A reactive flow model for hot-spot ignition of shocked aluminized explosives with small size aluminum grains [J]. Simulation Transactions of the Society for Modeling & Simulation International, 2017, 93(3):177-183.

[32] BAKER E L, CAPELLOS V, STIEL L I, et al. Accuracy and calibration of high explosive thermodynamic equations of state[J]. Journal of Energetic Materials, 2010, 28(Sup.1): 140-153.

[33] GOGULYA M F, MAKHOV M N, DOLGOBORODOV Y A, et al. Mechanical sensitivity and detonation parameters of aluminized explosives[J]. Combustion, Explosion and Shock Waves, 2004, 40(4): 445-457.

[34] GOGULYA M F, BRAZHNIKOV M A. Effect of the dispersity of the components of explosive materials on the detonation velocity and sensitivity to mechanical action[J]. Russian Journal of Physical Chemistry B, 2010, 4(2):286-303.

[35] GREBENKIN K F. Comparative analysis of physical mechanisms of detonation initiation in HMX and in a low-sensitive explosive (TATB) [J]. Combustion, Explosion, and Shock Waves, 2009, 45(1): 78-87.

[36] YILMAZ G A, SEN D, KAYA Z T, et al.. Effect of inert plasticizers on mechanical, thermal, and sensitivity properties of polyurethane-based plastic bonded explosives [J]. Journal of Applied Polymer Science, 2014, 131(20): 1-8.

[37] ZHANG Z Y. Studies on high pressure reaction rate of PBX-9404 [J]. Explosion and Shock Waves, 1999, 19(4): 360-364.