科技型企业财务危机预警研究

潘雅琼 刘艳

【摘 要】 从2000—2018年在沪深两市主板上市的科技型企业中选取样本，并从财务状况、公司治理、科技创新能力三个方面选择预警指标，运用生存分析法构建Cox比例风险模型进行实证研究，结果显示：国有股比率、产权比率是危险因子，指标值越大，企业发生财务风险的可能性会相应增加;而研发投入金额、流通股比率、董事会议次数、营业利润增长率、现金流动负债比是保护因子，指标值越大，可以降低企业发生财务危机的概率。进而绘制了生存函数曲线，发现企业生存率变化波动最大的时刻为上市70个月和150个月，此时发生财务危机的概率较大。最后对模型的判别能力进行检验。

【关键词】 财务预警; 生存分析; Cox比例风险模型; 科技型企业

【中图分类号】 F275  【文献标识码】 A  【文章编号】 1004-5937（2021）08-0064-07

一、引言

随着经济全球化进程的深化，企业间的竞争愈加激烈，遭遇财务危机的可能性也不断增加，财务预警多年来都是国内外研究的热点问题。所谓财务预警，即运用风险管理的相关理论和方法，分析企业面临的宏观环境、微观治理、经营状况、财务管理等，对企业的财务风险状况进行识别、评估、预测并发出警示信号，以便企业防范规避风险。科技型企业由于产品更新换代的周期短，必须不断创新以保持其在技术上的优势，因此具有高投入、高风险、高回报并存的特点。这些特点决定了科技型企业的财务风险远高于其他企业。在此情形下，科技型企业迫切需要一套财务预警机制来防范风险。生存分析法（Survival Analysis）作为一种动态的统计分析方法，研究特定事件发生的概率、时间及其影响因素的规律，最初在生物医学领域应用较多，因其具有动态分析发生财务危机的概率随时间变化的规律、处理删失数据等优越性，而被学者们引入金融、财务等领域。鉴于此，本文顺应科技型企业加强财务预警的内在诉求，基于生存分析法构建预警模型，以期为科技型企业的持续健康发展提供指导和借鉴。

二、文献综述

（一）财务预警方面的研究

在财务预警体系的构建中，学者们选择的指标主要包括：传统的财务比率指标，如选取偿债能力、盈利能力、营运能力、发展能力[1-2]等预警指标，考察企业的基本财务能力;现金流量指标，学者们分别从经营现金流量负债比率[3]、销售收入现金量[4]、净资产获现率[5]等方面选取指标，考察企业的现金充裕程度和流入流出变动状况;公司治理指标，通过前十大股東持股比例之和、Z指数[6]、独立董事比例[7]等指标，考察公司的董事会规模、股权结构等内部治理环境的合理程度。

财务预警研究方法主要包括两大类：一是经典的统计方法，如单变量分析、多元判别分析、Z-score模型[8]、logistic回归[9]、probit回归等;二是人工智能方法，如神经网络、决策树、支持向量机等方法。李扬等[10]应用加权L1正则化支持向量机（w-L1SVM）对SVM进行了改进，解决了由于财务危机企业远少于正常企业带来的数据不平衡问题，提高了预测的准确率。王昱等[11]采取人工神经网络、决策树技术，考虑经营、财务、融资、人力资本多维效率，运用数据包络研究上市公司的财务困境预警。

（二）生存分析方面的研究

20世纪60、70年代，在生物医学、药学领域人们开始应用生存分析法，研究病人的术后存活率、康复时间以及药物的临床试验效果，后来被引入经济学领域，研究出口贸易关系[12]、股市涨跌预测[13]、违约概率测算[14]等。少数学者在研究企业财务预警时尝试采用生存分析法，测算企业发生危机的概率，预测其生存时间。Gemar et al.[15]用该方法发现住宿行业企业的生存概率取决于企业的地理位置、财务状况、公司特征。Matsuno et al.[16]在测度日本信息服务企业的生存概率时，发现软件开发、系统集成和委托加工这三种销售比率具有显著的正向影响。Lagares et al.[17]运用生存分析法研究西班牙水产养殖业，发现具有良好的长期偿债和盈利能力、较好履行环境承诺、经营年限较短的企业，其生存概率较大。还有学者则运用生存分析法研究公司治理结构[18]等指标在企业财务预警中的作用。

生存分析法中的模型具有普适性，在行业的选择上没有太多限制要求，其适用性与行业无关。一些学者已将该方法运用于高科技行业的相关问题研究中，如：张春香等[19]聚焦于新创高科技企业，建立生存分析模型研究声誉对其风险投资获得时间的影响;刘瀚龙等[20]也着眼于高技术企业，基于生存分析研究政府规制负担与企业生存概率的关系。本文试图用生存分析法研究科技型企业的财务预警问题，考虑到这类企业具有资金投入大、知识和技术密集、创新能力强、高风险等与传统行业迥然不同的特点，在构建生存分析模型时除了传统的财务及公司治理指标，需要引入更符合科技型企业特点的创新能力指标，对经典模型进行扩展以使此类企业的风险预警更加精准，这也是本文可能的创新之处。

综上，虽然在财务预警领域已经有不少的研究，但其着眼的指标大多是传统的财务比率、现金流量或公司治理指标，科技创新等因素较少涉及;采用的研究方法多局限于静态分析，或是修正经典模型，或是对比多种研究模型的预测精度。因此，本文借鉴前人的研究成果，引入生物医学领域的动态分析方法——生存分析法，它弥补了传统静态研究方法的不足，能全面展示企业历年来财务状况的变化规律，测算企业可能发生风险的时点和概率，及时预警。此外，本文选择科技型企业这一前人较少关注的行业进行生存分析，基于企业的经营特点，加入了创新能力指标，考察科技型企业的创新资金和创新人才投入力度以及产出创新成果的效率。从创新能力、公司治理和财务状况三个方面综合构建预警指标体系，指标考量更加全面，为科技型企业规避财务风险、摆脱财务困境提供针对性指导，具有一定的现实参考价值。

三、生存分析方法论

（一）生存分析概念

生存分析是研究相关因素对特定事件是否发生（如死亡、违约、破产等）及发生时间的影响及其统计规律的一种动态分析方法。生存分析常用的估计方法主要有三种：非参数法、参数法和半参数法。其中Cox比例风险模型为半参数法，应用最为广泛，是由Cox D. R（1972）提出的一种对生存时间的分布无限制、可以处理含有截尾数据样本的模型，用来分析多种因素对研究对象生存时间的影响。其中的生存数据包括两种：一种是完全数据，指的是可以完整观测到其生存时间的起点和终点的样本数据;另一种是截尾数据，即在观测期内因各种原因（失访、中途退出、观测期截止等）导致所要研究的特定事件的开始时刻或终止时刻的数据出现缺失的样本数据。

（二）生存分析基本函数

生存分析中包含生存函数、累积分布函数、风险函数、累积风险函数四种基本函数，它们之间可以相互推导转化。其中，生存函数反映的是研究对象在经过时点t后仍存在的概率。其基本形式为：

研究中采用最多的生存分析模型是Cox比例风险模型，基本函数形式是：

公式2中，S（t，x）为生存函数，即生存率。S0（t）的影响因素仅包括研究对象的生存时间t，其余外界因素对其无任何影响，为基准生存函数。Xi为协变量，表示可能给研究对象的生存带来某些不确定影响的因素，即财务预警指标。βi为计算出的协变量的系数，显示了每个可能的因素Xi对其生存率影响程度的大小。其中，对参数βi的估计需要用到Cox提出的偏似然函数，即：

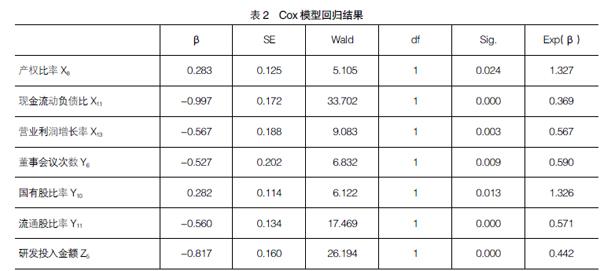
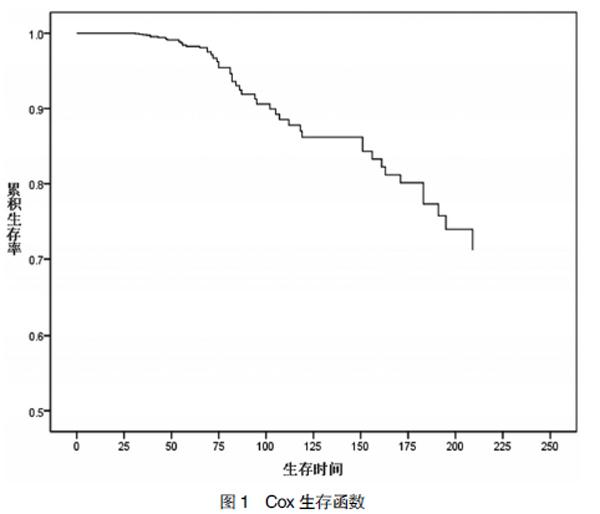
公式3中，设ti（t1<…ti…

四、实证分析

（一）指标选取与模型构建

根据上述Cox比例风险模型的基本形式，本文将X设为代表财务能力指标的向量，Y设为代表公司治理指标的向量，Z设为代表创新能力的向量。λ、ε、η则为代表三个维度变量系数的向量，显示三个不同维度的影响因素指标对企业生存率的作用程度大小。最终建立如公式4所示的生存分析模型：

企业财务危机形成的原因复杂多变，需要多方考虑。本文着眼于财务能力、公司治理、创新能力三个维度，变量X1，…，X27的选择综合考虑了企业的偿债、盈利、营运、发展能力和现金流量等对企业财务能力的影响，变量Y1，…，Y11的选择则是考虑到管理层和股权结构等对公司治理的影响。此外，在创新能力指标方面，已有许多的研究文献做过系统的阐述。企业的创新能力一方面取决于企业的创新资源投入，如企业科研人员占比、R&D经费投入等人力和财力的投入。另一方面取决于企业的创新绩效，如企业申请发明专利数、科技成果获奖数等体现企业创新产出效率的指标。因此，本文借鉴支军等[21]、徐立平等[22]提出的企业创新能力评价与测度指标体系，选取了Z1，…，Z5这5个反映企业创新资金和人员投入、成果产出的变量。最终初步构建的财务预警指标体系及对每个指标的假设如表1所示。

（二）样本数据来源

本文中作为样本的企业均是被政府有关部门资质审核认定为“高新技术企业”或“软件企业”的科技型企业，并且在沪深两市主板上市。最终筛选出來的样本企业总共有260家，其中被特殊处理（ST）的样本70家，在观测期间始终正常且未被ST的企业样本190家。为进行样本外检验，验证模型的准确性，随机选择保留了60家企业样本，剩余的200家企业样本数据（正常样本145家，ST样本55家，）则作为建模样本。本文中企业样本的相关数据全部来自于政府网站、上市公司财务年报、CSMAR、RESSET经济金融数据库。

（三）生存时间界定

本文的观测时间设置为2000—2018年。生存时间以月为尺度进行计算，生存时间的起点均为企业首次挂牌上市之时，对于生存时间终点T的设置，截尾数据（非ST企业）的生存终点为2018年12月31日，即观测期末，完全数据（ST企业）则以企业第一次被特殊处理（ST）的时刻为生存终点。鉴于国内证券交易所决定企业是否应被“ST”的直接依据是企业前两年的经营财务情况，为了确保最终模型预测结果的科学性，本文搜集整理数据时摒弃了T-1和T-2年的数据，而选择T-3年的数据纳入模型进行研究，因此，最终筛选出的样本中企业首次上市时间最晚不超过2015年。

（四）数据处理及实证过程

1.显著性检验

在对原始数据进行缺失值及标准化处理的基础之上，本文采用Mann-Whitney U检验对所有的变量进行显著性检验，初步判断在ST企业和非ST企业中这些指标是否表现出明显的差异。最终的检验结果表明，X12（P=0.143）、X14（P=0.481）、X17（P=0.997）、X18（P=0.729）、X19（P=0.927）、X20（P=0.225）、X26（P=0.947）、Y2（P=0.473）、Y3（P=0.061）、Y8（P=0.124）、Y9（P=0.554）、Z3（P=0.170）、Z4（P=0.597）这13个指标的P值全都大于0.05，没有通过显著性检验，因此这些变量不能纳入研究模型，将其剔除。

2.多重共线性检验

通过Spearman相关分析，发现X2、X5、X27这三个指标的相关系数高于0.7，因此将其去除。接着对余下的27个指标的多重共线性进行检验，最终的诊断结果中每个变量的容忍度（TOL）和方差膨胀因子（VIF）这两个指标的大小都符合“TOL>0.1，VIF<10”这一判断标准，因此，可以基本上判定这27个变量间不存在多重共线性。

3.Cox模型回归

将通过上述过程筛选出的27个变量纳入Cox模型进行回归。回归过程通过SPSS软件实现，采用“Forward：LR法”让协变量进入模型，设定进出模型的概率均为0.1，在5%的显著性水平迭代回归多次后，得到如表2所示的模型回归结果。从表2中可以看出，最终只有7个关键指标会对模型的结果产生显著的影响，且变量的显著性全都小于0.05，表明模型在5%的显著性水平上具有解释力。

4.比例风险假设PH检验

由于Cox模型的构建需要满足一个重要的假设——模型中协变量对风险率的影响（即Hazard Ratio）不会随着时间的推移而发生改变，所以需要对Cox模型回归的结果进行比例风险假设检验，基于表2中的回归结果，在Stata软件中输入命令“estat phtest，detail”以检验回归得到的Cox模型是否符合PH假设。结果显示其协变量X8、X11、X13、Y6、Y10、Y11、Z5的显著性分别为0.78、0.15、0.63、0.15、0.60、0.90、0.14，全都大于0.05，同时Global test一行代表模型整体的检验结果，其显著性的值为0.61，也大于0.05，不能拒绝PH假定，说明Cox回归结果是满足比例风险假设的。

（五）实证结果分析

回归结果显示，X11、X13、Y6、Y11、Z5的系数β分别为-0.997、-0.567、-0.527、-0.560、-0.817，全部都小于0，说明这些变量可以降低财务风险，是保护因子。而X8、Y10的系数β分别为0.283、0.282，都大于零，说明这些变量会增加发生财务危机的概率，是危险因子。

从保护因素的角度看，现金流动负债比的相对危险度Exp（β）值为0.369，表明指标X11值越大，企业赚取现金的能力越强，对短期债务的偿付能力越强，财务风险越小。营业利润增长率的Exp（β）值为0.567，同理，该指标值越高，表明企业营业利润增长速度越快，反映出企业的经营业务市场前景较好，具有持续性的利润增长点，具备长期发展的潜力，发生风险的可能性越低。董事会议次数的Exp（β）值为0.590，表明如果公司的股权所有者更多地召开董事会，则更有利于其履行对经营者的监督管理职责，经营决策科学性更强，企业的经营风险也随之降低。流通股比例的Exp（β）值为0.571，说明如果企业可以在市场中自由交易流通的股票数占比越高，则公司的所有权更为分散，不会出现“一言堂”，经营决策风险更低。研发投入金额的Exp（β）值为0.442，表明对于科技型企业来说，研发投入总额越多，则企业产品的更新换代能力越强，在竞争中更有优势，风险更小。

从危险因素上看，产权比率反映企业举债经营的程度，其Exp（β）值为1.327，表明如果企业的产权比率指标越高，则企业的总资产中自有资金占比越低，过多地依赖于债权人提供的资金进行日常经营，资金结构不够合理，导致企业偿还长期债务的能力较弱，风险过大。国有股比率反映国有资本对企业的控制程度，其Exp（β）值为1.326，表明若企业的股权结构中属于国有的股份比重过高，则企业的经营和管理就更有可能因为组织结构灵活性不够、效率低下而缺乏市场竞争力，更容易陷入财务困境，风险更高。

（六）生存函数图

此外，通过回归还可以得到如图1所示的生存函数图，其中，横纵坐标分别代表着企业上市后生存时间和累积生存率，它可以直观地显示出随着时间的推移，企业在不同时点累计生存率的波动趋势。通过图1可知，企業生存的第一个高危时段存在于上市70个月（5.8年）时，在这一时点之后，企业累积生存率有一个较大幅度的下跌，说明处在这个时间段的企业有很大可能陷入财务困境。而第二个高风险的时段存在于上市150个月（12.5年）之时，企业的生存率同样下降得十分迅速，经营风险较大。

（七）基准生存函数的估计

Cox回归完成后，就能通过表2的回归结果知晓每个协变量的系数β的值，此外，还需要求解基准生存函数S0（t）的函数形式，才能确定Cox模型的最终形式。通过归纳和总结其他学者的研究，可知基准生存函数S0（t）的分布形式具有不确定性，需首先假设其满足某一特定分布形式，因此，本文假设S0（t）满足指数分布。同时，基于寿命表法可以计算出不同的生存时间t所一一对应的企业生存率，得出具有对应关系的基准生存率表。

基于上述假设，可知S0（t）的基本形式为：S0（t）=e-λt，将左式两边取对数，可将其转化为Ln[S0（t）]=-λt，通过代数替换，即令X=t，Y=Ln[S0（t）]，将其转化为一次函数的形式Y=-λt，最后，将前面得到的基准生存率表中数据代入，进行一元线性回归，求得的模型的拟合优度达到了0.96，说明其满足指数分布的假设是可行的。

线性回归进行参数估计的结果显示其常数项显著性为0.114，大于0.05，不显著，一次项X的显著性为0.000，且系数为-0.002，则可以得到回归出的线性函数表达式为Y=-0.002X，与之前假设的指数分布形式Y=-λt一致，因此可以得到Ln[S0（t）]=-0.002t，最终得到基准生存函数的表达式为S0（t）=e-0.002t，则Cox模型最终形式为：

（八）模型的预测能力检验

检验模型的判别能力，需要设定一个判别点，生存分析理论上不存在最优判定点，在判别分析与Logit回归研究中，研究者通常将判别点的取值定为0.5，因此，本文遵照此判断标准，将生存率大于0.5的企业判为正常企业，生存率小于0.5的企业判为ST企业，表3中显示的就是最终的预测统计结果。从表中可知，以0.5为判定点，模型在原始的建模样本中表现较好，预测精度高达86.5%，在进行样本外检验时模型的预测精度（81.7%）仅有一定的降低，但相较而言降幅较小，且二者的综合预测准确度为85.4%，波动性较小，说明模型的预测结果具有稳定性，预测能力良好。

五、结论

本文以沪深两市主板的260个科技型上市公司的数据样本进行实证研究，从财务状况、公司治理、创新能力三方面选取财务预警指标，利用生存分析法中的Cox比例模型进行回归，得出影响科技型企业生存率的7个关键指标，绘制生存曲线，得到企业生存率随时间动态变化的规律，并对模型的预测能力进行检验，整体预测精度为85.4%。

实证结果显示，若研发投入金额、流通股比率、董事会议次数、现金流动负债比、营业利润增长率这5个关键的指标值越大，对企业的财务风险的减小可以起到积极的影响，是保护因子。产权比率、国有股比率2个指标值如果过大则会增加企业发生财务危机的概率，是危险因子。因此，对于科技型企业，从财务状况来看，提升企业经营活动中的盈利能力，并维持企业充足的现金来源，避免过高的负债比率，对于削弱企业的财务风险有重要的作用。从公司治理的情况来看，董事会需要加强对企业事务的关注度，并对经理层进行监管，还要保证企业能自由流通的股份占有较大的份额，以使股权尽量分散，同时，可以逐渐降低和调整国有股权比例，形成多元化的股权结构，以降低管理中的风险。从企业创新的角度来看，科技型企业之间的竞争依靠的就是技术的先进性和独特性，而要提升企业的技术创新能力，培养这种技术上的核心竞争力，就必不可少地需要大量研发资金和相关人力物力的投入，同时还要关注企业的创新转化效率，只有创新成果的取得才能直接降低企业的经营风险。

【参考文献】

[1] DU JARDIN P.Dynamics of firm financial evolution and bankruptcy prediction[J].Expert Systems with Applications，2017，75：25-43.

[2] 阿小燕，趙娟.资源型上市公司财务预警实证分析[J].财会月刊，2018（2）：79-84.

[3] ALMAMY J，ASTON J，NGWA L N.An evaluation of Altman' s Z-score using cash flow ratio to predict corporate failure amid the recent financial crisis：evidence from the UK[J].Journal of Corporate Finance，2016，36：278-285.

[4] 刘翰林，张友棠，彭颖.基于现金流的上市公司财务预警研究——以信息技术业为例[J].财会通讯，2016（31）：24-27.

[5] BEN JABEUR S.Bankruptcy prediction using partial least squares logistic regression[J].Journal of Retailing and Consumer Services，2017，36：197-202.

[6] 鲍新中，陶秋燕，傅宏宇.基于面板离散选择模型的企业财务预警及其行业适用性[J].系统管理学报，2016，25（1）：36-44.

[7] MIGLANI S，AHMED K，HENRY D.Voluntary corporate governance structure and financial distress：Evidence from Australia[J].Journal of Contemporary Accounting & Economics，2015，11（1）：18-30.

[8] FITO M A ，PLANA-ERTA D，LLOBET J.Usefulness of Z scoring models in the early detection of financial problems in bankrupt Spanish companies[J].Intangible Capital，2018，14（1）：162-170.

[9] KRISTANTI F T，RAHAYU S，HUDA A N.The Determinant of financial distress on indonesian family firm[J].Procedia - Social and Behavioral Sciences，2016，

219：440-447.

[10] 李扬，李竟翔，马双鸽.不平衡数据的企业财务预警模型研究[J].数理统计与管理，2016，35（5）：893-906.

[11] 王昱，杨珊珊.考虑多维效率的上市公司财务困境预警研究[J].中国管理科学，2020（7）：1-12.

[12] 张亚斌，黎谧，李静文.制造业出口贸易生存分析与跨国比较研究[J].国际贸易问题，2014（11）：3-13.

[13] 贺筱君，陈俊男，吴佳懋.生存分析在股市期市涨跌预测中的应用[J].数量经济技术经济研究，2014（12）：116-122.

[14] DIRICK L，CLAESKENS G，BAESENS B.Time to default in credit scoring using survival analysis：a benchmark study[J].Journal of the Operational Research Society，2017，68（6）：652-665.

[15] G？魪MAR G，MONICHE L，MORALES A J.Survival analysis of the Spanish hotel industry[J].Tourism Management，2016，54：428-438.

[16] MATSUNO S，UCHIDA Y，TSUTOMU ITO，et al.A survival analysis of the Japanese information service industry[J].Procedia Computer Science，2017，121：291-296.

[17] LAGARES E C，ORDAZ F G，HOYO J G.Innovation，environmental commitment，internationalization and sustainability：A survival analysis of Spanish marine aquaculture firms[J].Ocean and Coastal Management，2018，151：61-68.

[18] 孙奕驰，张艺馨.上市公司治理风险预警研究——基于时依协变量的COX 模型[J].会计之友，2011（2）：65-67.

[19] 张春香，张百舸.新创高科技企业声誉对其风险投资获得时间的影响——基于Cox比例风险模型的实证分析[J].技术经济与管理研究，2018（9）：57-61.

[20] 刘瀚龙，范黎波，李德辉.政府规制负担降低了高技术企业的生存概率吗？——基于微观企业的经验分析[J].财经论丛，2018（6）：96-103.

[21] 支军，王忠辉.自主创新能力测度理论与评估指标体系构建[J].管理世界，2007（5）：168-169.

[22] 徐立平，姜向荣，尹■.企业创新能力评价指标体系研究[J].科研管理，2015（36）：122-126.