基于集成学习与特征降维的小样本调制识别方法
2021-04-07史蕴豪郑万泽刘英辉
史蕴豪, 许 华, 郑万泽, 刘英辉
(空军工程大学信息与导航学院, 陕西 西安 710077)
0 引 言
通信信号调制方式识别是通信侦察、认知电子战领域的关键技术之一,在实际战场环境中,由于敌我双方的非协作特性,使得在还原敌方通信信号、获取敌方情报信息之前必须进行调制方式识别。此外,通信信号调制方式识别也为后续的信号解调、比特流分析、协议识别、信号解密、灵巧干扰等提供了重要支撑。
调制识别技术发展至今,无论是传统方法还是近些年兴起的深度学习方法均已取得杰出的研究成果。传统方法方面,文献[1-3]利用信号高阶累积量实现调制信号分类,文献[4-5]通过提取信号循环谱特征区分信号不同调制方式,文献[6-7]利用信息熵特征实现信号分类。深度学习方法方面,O’shea等人[8-9]最早于2016年利用有监督深度学习技术实现调制方式识别,直接使用卷积神经网络构建端到端的学习模型,成功对11种数字或模拟调制方式进行了识别。Jeong等人[10]提出利用短时傅里叶变换将信号从时域转换为时频域,并通过深度卷积神经网络提取时频域特征,最终完成了7种调制方式的识别,其在-4 dB的信噪比下仍有90%以上的识别正确率。Fan等人[11]提出了一种联合噪声估计的调制识别算法,该算法同时将原始信号数据和信噪比作为神经网络的输入,仿真结果显示这种算法在不同信噪比和不同频偏下的识别成功率已经接近理论识别率的上限。Zhang等人[12]利用卷积神经网络提取信号SPWVD时频图特征和BJD时频图特征,并与大量手工特征融合对8种调制方式进行识别,在信噪比为-4 dB时仍有92.5%的识别准确率。
虽然近些年基于深度学习的调制识别方法在识别性能方面逐渐超越传统人工特征方法,但是深度学习类方法需要大量带标签信号样本作为支撑,一旦带标签样本量不足,模型的识别性能就会发生急剧下降。随着信号采集方式的多样化以及存储技术的高速发展,现阶段获取大量无类别标记信号样本变得相当简单,但是若想获得同样量级的有类别标记信号则相当困难,这是由于数据的类别标记工作一般需要耗费大量的人力、物力和时间。在实际战场环境中,电磁频谱中会出现大量信号,将这些信号采集下来后逐一打上标签是不现实的,无法适应瞬息万变的战场态势,因此研究有标签信号样本不足的小样本调制识别问题就显得尤为重要。
通过总结大量专家研究成果发现,小样本问题产生的根本原因是传统方法通过固定模式处理信号序列提取信号特征,从而可利用低维度特征表示信号。然而,深度学习类方法由于网络参数多、拟合难,需要大量的样本才能完成低维特征提取。另一方面,分类器训练特征时所需样本量也是随着特征维度呈指数增长。因此,如何有效减小特征数量,并尽可能利用低维度特征表示高维信号序列是解决小样本问题的核心所在。若能利用低维度特征表征原始时序信号,则可极大减小分类器所需训练样本。针对上述思路,本文提出一种基于集成学习与特征降维的小样本调制方式分类模型。该模型通过集成人工设计特征与机器学习自动提取特征构成融合特征集,再针对性地设计特征选择算法对融合特征集进行优选生成高效特征子集,最后设计高性能分类器对少量有标签信号进行训练,从而解决有标签训练样本不足导致的小样本问题。
1 识别模型
基于集成学习与特征降维的小样本模型本质思想是利用低纬度特征表征原始信号,降维对高维小样本问题行之有效,信号降维主要包括特征提取和特征选择两方面。本文拟提取信号最具表征性、区分度的特征并降维,从而达到减少有标签训练样本数的目的。如图1所示,本文算法主要分为3个阶段,第1阶段为特征提取阶段,利用传统方法提取对信号区分能力强的人工特征,与此同时利用机器学习类方法中的自编码器网络对样本进行无监督训练,自动提取低维信号特征,而后将两类特征进行融合重组。第2阶段为特征选择阶段,运用自主设计定的特征选择算法综合选出一定数量的最具区分能力的特征,生成最优特征子集。第3阶段为分类阶段,利用少量有标签样本对高性能分类器进行有监督训练,从而完成信号小样本条件下的分类识别。
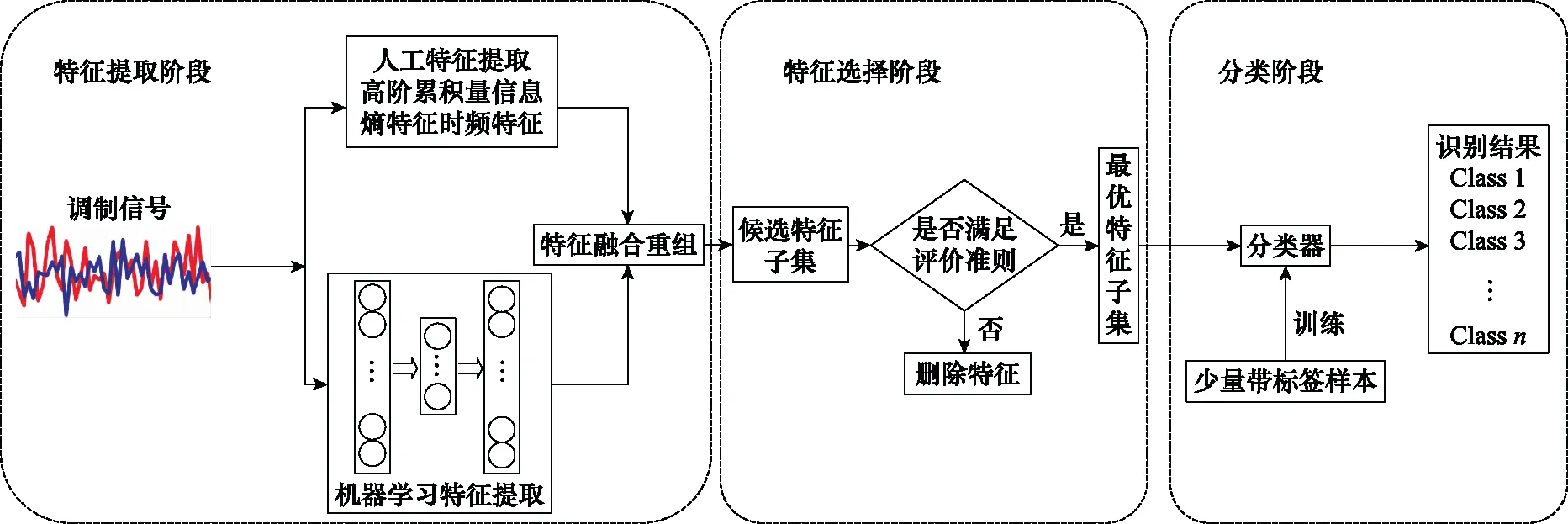
图1 算法总体框架
2 信号特征提取
2.1 人工特征提取
在调制识别领域中,众多研究人员已进行大量特征工程研究,设计了很多卓有成效的特征用于信号分类,并取得了优异的结果。因此,利用前人的研究成果提升信号分类效率是重要的研究切入点。本文拟提取多类表征性强、区分度高的特征作为信号人工特征,包括信号高阶累积量、信息熵特征以及时频特征。
2.1.1 信号高阶累积量特征
在调制技术领域,高阶累积量是应用非常广泛的特征之一,由于其具有较强的周期分量,可用于准确识别不同的调制信号。为提取高阶累积量,首先要计算信号的高阶矩,序列信号x(n)的高阶矩计算公式为
Mp q=E[x(n)p-q(x*(n))q]
(1)
通过信号各阶高阶矩便可计算得到各类高阶累积量,本文选择下列高阶累积量,这些累积量均已被证明在调制信号分类识别中有较好鉴别能力[13-14],即
(2)
(3)
(4)
(5)
(6)
2.1.2 信息熵特征
熵是用于评价信号或系统状态平均不确定性的指标。在信息论领域,熵用于衡量信息的信息量,信息的不确定程度越大,则其熵值越大,因此信息熵理论提供了一个很好的信号特征描述方法。本文拟提取信号的功率谱熵、奇异谱熵和能量谱熵,以此作为信号的特征[15]。
(1)功率谱熵
假设时间序列X长为L,对其进行离散傅里叶变换,变换结果为
(7)
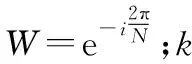
(8)
记
(9)
将式(9)代入香农熵计算公式,即可得到功率谱香农熵。
(2)奇异谱熵
奇异谱分析是近年来非常流行的一种研究非线性时间序列数据的方法,其结合相空间重构和奇异值分解对时间序列维数进行估计。假设一段离散时间序列为
X=[x1,x2,…,xN]
首先将信号分段,假设分段长度为m,在奇异谱分析过程中,m最好为信号周期的整数倍且不宜超过信号序列长度的1/3,重构后的序列轨迹矩阵为
(10)
对式(10)进行奇异值分解,可得
(11)
式中,U和V均为正交矩阵;U为左奇异矩阵;V为右奇异矩阵;Σ矩阵可化为对角阵,即
式中,σk表示矩阵M的奇异值且除对角线上元素以外其余值均为零,对角线上的非零元素便构成了序列的奇异值谱,即
σ={σ1,σ2,…,σi,…,σj|j 记pi表示非零奇异值σi占所有非零奇异值之和的比值: (12) 将式(12)代入香农熵计算公式,即可得到奇异值香农熵及奇异谱指数熵。指数熵的计算公式为 H=E[e1-pi]=∑pie1-pi 式中,H表示熵值;pi表示信号概率分布。 (3)能量谱熵 对于序列信号X=[x1,x2,…,xN],其能量谱定义为 (13) 式中,X(ω)表示序列X的傅里叶变换。记pi为 (14) 将式(14)代入指数熵计算公式,即可得到信号能量谱指数熵。 2.1.3 归一化中心瞬时振幅的功率密度最大值 归一化中心瞬时振幅的功率密度最大值可在一定程度上反应不同信号的谱特征[16],其定义为 (15) ac n(i)=an(i)-1 (16) an(i)=a(i)/ma (17) (18) 式中,Ns表示信号序列长度;ma表示信号瞬时幅度的均值。 自编码器作为一种无监督机器学习算法可以在不借助标签信息的前提下学习数据的稀疏表示,近些年已有许多学者将其应用至信号调制方式识别中。例如,文献[17]使用两个并行自编码器完成信号调制方式识别,文献[18]利用卷积自编码器直接作用于信号序列以提取信号特征。 自编码器结构包括编码器和解码器两部分,输入数据首先通过编码器进行降维操作,再通过解码器进行数据重构,通过约束中间层的维度并最小化重构数据与输入数据间的误差,从而达到特征映射的目的,在整个过程中虽然并未涉及输入信号的标签信息但却完成了信号特征提取的功能。本文设计了图2所示的自编码器结构用作信号特征自动提取,自编码器网络总体上由卷积层和全连接层构成。在信号输入自编码器网络之前,首先对信号进行加噪处理,由于通过自编码器后需重构原始无噪数据,因此自编码器提取的特征具有抗噪能力,也更具鲁棒性。本文网络选用高斯噪声干扰信号,噪声系数为0.1。信号输入后首先通过两层卷积层对其进行特征提取,而后通过三层全连接层对特征进行降维、再升维处理,最后再通过两层卷积层对信号进行重构,使得网络输出信号格式与输入格式保持一致。 图2 自编码器结构 (19) 式中,f(x)表示自编码器中编码器函数部分;h(x)表示自编码器中解码器函数部分。通过最小化损失函数,约束输入输出之间的重构误差,便可以低维中间层特征表示高维信号,从而达到特征提取的目的。 与前两节所述的特征提取方法不同,特征选择方法指的是从全部原始特征集中选择最相关的特征子集以此降低特征向量维度。相较于特征提取方法,特征选择方法更加侧重于揭示特征与特征间、特征与类别间的因果关系。在以往的调制方式识别算法中,选用传统手工特征还是利用机器学习方法自动提取信号特征一直存在争议,两类方法也各自具有优势,因此本文先对两类特征进行融合,再使用特征选择算法进行综合筛选,选取其中最具区分度的特征。一个好的特征选择算法不仅可以帮助降低训练分类器所需样本数量,剔除冗余或不相关特征,还可以提升模型运行速度,加快算法收敛速度和降低硬件要求。 由于本文研究的是小样本条件下的信号识别问题,因此在特征选择时既有少量有标签的信号,同时还存在大量无标签的信号,即需要使用半监督特征选择算法进行特征选择。近些年,国内外学者也提出了各式各样的特征选择算法,例如文献[19-25]。其中,文献[24]通过信息熵理论设计了随机变量的对称不确定性,用于度量特征与特征之间的冗余性、特征与类别之间的相关性,在多个数据集上均有良好的表现;文献[25]则最大程度的利用了无标签样本,确保了所选特征子集优于仅用有类别标记数据的特征选择算法。本文综合文献[24]的快速过滤特征选择(fast correlation-based filter, FCBF)算法和文献[25]的半监督代表特征选择(semi-supervised representatives feature selection, SRFS)算法设计了新的半监督特征选择算法。 该方法的流程图如图3所示,整个特征选择过程主要分为两个阶段,具体内容如下。 图3 特征选择过程 (1)删除不相关特征 有标签信号可利用标签信息直接求出特征与标签之间的互信息量作为衡量特征重要性的标准。互信息是两个随机变量共同信息量的度量,假设特征为随机变量X,信号标签为C,p(x)、p(c)和p(x,c)分别表示X、C、(X,C)的概率密度函数,则随机变量X与C的互信息量I(X,C)定义为 (20) 无标签信号虽然没有标签信号可以利用,但是其本身包含的自信息量也可在一定程度上指导特征选择。在信息论中,熵可用来度量特征自身包含的信息量,对于随机变量X,熵的计算公式为 (21) 当计算出各个特征与标签的互信息量与自信息量后,通过F-相关性判别特征Fi是否为不相关特征,F的计算公式为 F_Rel(Fi,C)=βI(Fi,C)+(1-β)H(Fi) (22) (2)删除冗余特征 第一步删除不相关特征后得到去相关特征子集{F1,F2,…,FM},将待选的特征按照F-相关性进行降序排列,F-数值越大则排名越靠前。而后从前到后依次计算特征与类别间的F1-相关性,以及特征与特征之间的F2-相关性,F1-的计算公式为 F1_Rel(Fi,C)=βUI(Fi)/H(Fi)+(1-β)SU(Fi,C) (23) 式中,UI(Fi)表示特征Fi与其他所有特征的互信息量的均值;SU(Fi,Fj)为特征Fi与Fj的对称不确定性。其计算表达式分别为 (24) (25) F2-的计算公式为 F2_Rel(Fi,Fj)=βSU(Fi,Fj)+(1-β)USU(Fi,Fj) (26) 式中,USU(Fi,Fj)表示特征Fi与Fj的无监督对称不确定性,具体表述为 (27) UI(Fi;Fj)=UI(Fi)-UI(Fi|Fj)= (28) 本文设定式(29)为冗余判别条件,若满足该条件则将Fj视为冗余特征删除,在删除过程中优先保留F-排序靠前的特征,迭代结束后最终剩余的即为最终选出的特征子集。 F1_Rel(Fi,C)≥F1_Rel(Fj,C)∩F2_Rel(Fi,Fj)≥ F1_Rel(Fj,C) (29) 本文选用的调制信号集为{BPSK、4PSK、8PSK、8QAM、16QAM、64QAM、4PAM、8PAM},共计8种调制信号。各个信号序列长度L=128,包括I、Q两路数据,信号数据格式为[2, 128],训练集每类信号生成5 000个信号样本,信噪比随机,共计40 000个信号样本。这其中包含800个带标签信号样本,每类100个,其余均为无标签样本;测试集每个信噪比点生成100个样本,信噪比从-10 dB至20 dB,间隔为2 dB,共计16个信噪比点,12 800个信号,所有信号均由Matlab R2016a仿真生成。 网络训练均基于Python下的tensorflow、keras深度学习框架实现,硬件平台中CPU使用Intel(R)Core(TM)i7-8700, GPU使用NVIDIAGeForce 1060。 本节将对第2节遴选出的人工特征性能进行仿真验证,实验对8类调制信号在-10 dB至20 dB间每个信噪比点取100个样本,提取信号的10种人工特征并取平均值,将其中具有代表性的特征并绘图,得到如图4所示的特征曲线。在进行信号奇异谱分析时,由于信号序列长度L=128,且基带序列为随机生成无周期特性,因此设置分段长度m=43;在计算序列离散傅里叶变换时,由于要求傅里叶变换点数靠近序列长度且为2的整数幂,因此设置傅里叶变换点数N=128。由图4可以看出,随着信噪比的不断上升,不同类别信号的特征值差距逐渐增大并逐渐趋于平稳,这有助于对信号进行分类。但同时可以看出,每个特征均存在不好区分的调制类别,因此本文选择将所有特征融合起来再由特征选择算法进行自动选择。通过本节可视化的特征实验可以看出,本文所选人工特征具有较好的调制信号区分能力。 图4 信号特征曲线 本节将对自编码器特征提取效果进行实验验证,使用每类5 000个无标签信号样本,共计40 000个无标签训练样本对自编码器进行无监督训练。自编码器结构如第2.2节所示,网络训练过程中batch_size设置为500,共迭代100个epochs。输入和输出间使用MSE衡量损失,使用ADAM优化器进行优化,网络输入、输出信号格式均为[2, 128]。训练结束后保存网络参数,再将所有信号输入网络进行计算,利用编码层对信号样本进行压缩,观察编码器与解码器的输出。信号压缩重构后的结果如图5所示,其中图5(a)~图5(d)分别表示BPSK、8PSK、16QAM、64QAM信号输入I、Q序列、输出I、Q序列、中间层编码器输出特征向量。 图5 自编码器输入输出 通过图5可以看出,经过自编码器重构后信号波形并未发生明显变化,这表示信号经过网络重构后输入端与输出端误差较小,意味着中间层的低维1×30特征在一定程度上可代表原始信号2×128的I、Q数据。 自编码器训练过程中的损失值随迭代次数的变化情况如图6所示,可以看出,随着网络不断迭代,输入与输出间的重构误差即训练损失不断减小,输入信号与重构信号不断逼近。 图6 自编码器训练损失 本节将对调制信号识别性能进行综合探究,首先利用第4.2节训练好的自编码器提取所有信号样本低维度特征,而后将低维度特征与第4.1节中的手工特征融合,共计40维送入特征选择器内,通过选择后生成优选特征子集,再利用少量带标签样本对分类器进行训练。 在本节实验中,送入特征选择器的特征集为{f1,f2,…,f40},其中前10维特征为手工特征{f1,f2,…,f10},分别代表{奇异谱香农熵、功率谱香农熵、C40、C42、C60、C61、C63、能量谱香农熵、奇异谱指数熵、归一化中心瞬时振幅功率密度最大值},后30维特征{f11,f12,…,f40}为自编码器网络自动提取的编码器输出层特征。 特征选择过程中,本文设定参数β=0.38,α=4。经过特征选择算法选择后,选出的最优特征子集为{f3、f7、f8、f9、f10、f12、f16、f19、f21、f27、f32、f36、f37}共计13维特征,所得特征比率为32.5%。 将特征选择后的13维特征子集送入分类器中,利用800个带标签信号对其进行监督训练。本文最终选择的分类器为浅层BP神经网络,之所以选择浅层BP网络作为特征分类器是因为浅层网络参数量级小,仅需少量训练样本就可快速收敛拟合,因此非常适用于本文设定的小样本场景。此外,BP网络相较于传统分类算法具有可学习性的优势,可自动学习各个特征对分类结果影响的权重,这在一定程度上也起到了抑制弱相关特征的目的。BP网络结构如图7所示,网络输入层神经元个数与特征维度相同,特征输入后首先对其进行批量归一化,而后接入全连接层,全连接层神经元个数分别为16、32、16,再将全连接层的输出送入Softmax分类器。各神经元均采用ReLU激活函数。为提升网络的泛化能力,在第2、第3层全连接层后使用Dropout技术干扰训练以防止网络过拟合,以提高网络在测试样本上的泛化能力,本文Dropout比例设置为0.1。 图7 BP网络结构 经过训练后分类器的识别性能如图8所示。其中,图8(a)表示信噪比为20 dB时的信号识别混淆矩阵,不同信噪比下各个信号的识别率如图8(b)所示,可以看出分类器在高信噪比条件下除对64QAM、8PAM的识别有一定错误率外,其余信号均可以做到准确识别,这在小样本条件下已是较好性能。 图8 本文算法在20 dB时识别性能 当不使用特征选择算法,分别直接利用10维手工特征、30维自编码器特征、40维融合特征对BP网络分类器进行训练,得到图(9)所示在信噪比为20 dB时的混淆矩阵。其中,图9(a)表示10维手工特征训练所得的混淆矩阵,图9(b)表示30维自编码器特征训练所得的混淆矩阵,图9(c)表示联合10维手工特征与30维自编码器不进行特征选择,直接送入BP网络训练所得的混淆矩阵。 图9 对比效果 通过图9可以看出,不论是分别采用某种单独方法或是联合特征后不进行特征优选,信号的识别性能相较本文算法较差。当利用10维手工特征时,信号最高识别率在20 dB为93.1%,利用30维自编码器特征时,信号最高识别率在20 dB为89.8%。当使用10维手工特征与30维自编码器不进行特征优选时,信号最高识别率在20 dB仅有83.7%。本文算法的识别率在信噪比大于14 dB时可达90%以上,最高识别率在20 dB时可达96%,可以看出通过特征融合优选后信号识别率得到了一定程度的提升。此外,可以看出当特征维度较高时信号识别性能有所下降,比如直接对40维特征直接进行训练,信号的最高识别率只有83.7%,这是因为在小样本条件下分类器无法对高维特征较好拟合所导致的性能下降。上述4类方法在各个信噪比点的识别率对比曲线如图10所示。此外,本节选择3类特征选择算法作为比较对象以验证本文特征选择算法的效果,分别为mRMR[26]、FCBF、SRFS。其中,mRMR、FCBF都是利用数据标签信息的有监督特征选择算法,SRFS是基于图论的半监督特征选择算法。考虑到上述3种算法中均需设置相关度阈值以剔除不相关特征,因此本节设定相关度阈值α=4与本文算法相同,在SRFS算法中设置控制变量β=0.38也与本文相同。由于对比的3种特征选择方法都与具体分类器算法是无关的,但需通过分类算法来评估特征选择方法所选特征子集的优劣,因此本节将各算法选择出的特征集送入BP网络,利用800个带标签样本进行监督训练,对比其分类识别准确率。各特征选择算法所选特征数目、特征子集与选择时间如表1所示。可以看出,不利用无标签样本的特征选择算法mRMR与FCBF的选择时间非常短,但其所选特征子集不够精简,而SRFS算法由于其需要构建有向无环图且仅从各子图中选取一个代表特征,因此其子集精简但比较耗时。 表1 各选择算法所选特征子集 图10 不同方法识别率对比曲线 各个算法所得特征比率如图11所示,其中mRMR所选特征比率为65%,FCBF所选特征比率为47.5%,SRFS所选特征比率为17.5%,本文算法所得特征比率为37.5%。 图11 特征比率直方图 将各特征选择算法选出的特征子集送入BP网络,利用少量带标签样本进行有监督训练,所得不同信噪比下的识别率曲线如图12所示。可以看出,本文算法所选出的特征子集相较于其他3种算法在浅层BP网络中的识别性能有一定优势。当信噪比为20 dB时,利用mRMR算法所提特征训练出的分类器最高识别率为90.5%,利用FCBF算法所提特征训练出的分类器最高识别率为92.1%,利用SRFS算法所提特征训练出的分类器最高识别率为93.9%,但均低于本文算法的96%。 图12 不同特征选择算法识别性能 为验证本文设计的浅层BP网络参数的最优性以及相较其他分类算法是否具有优势,本文首先对比不同激活函数、优化器、隐藏层层数条件下神经网络的识别性能,得到了图13所示的仿真结果。 图13 BP网络参数性能分析 通过实验结果可以看出,选用Relu激活函数的网络识别率相较于Sigmoid与Tanh激活函数有一定优势。基于Adam优化器的网络识别性能相较于SGD与Adagrad优化器有一定提升。在基于不同隐藏层数的对比实验中,本文堆叠经元个数为32的中间隐藏层,分别对比中间隐藏层数为1层、3层、5层时不同信噪比下的识别准确率,可以看出随着中间隐藏层数目的增加,网络识别准确率下降幅度很大。这是由于随着隐藏层数目的增加网络参数规模呈指数式上涨,仅有少量的有标签训练样本根本无法优化如此量级的网络,从而造成了严重的过拟合问题,最终导致识别性能的急剧下降。 最后,本文对比BP网络,XGBOOST分类器,KNN分类器[27]的识别性能,分别利用800个有标签信号的13维优选特征对上述3个分类器进行训练,得到各个分类器的收敛速度和最高识别率,如表2所示。对比实验中,所选的XGBOOST分类器为KERAS库中所属。可以看出浅层BP网络在训练时间基本相当的情况下,识别准确率较XGBOOST和KNN算法也有一些优势。 表2 不同分类器性能对比 本文针对实际战场中信号调制识别领域可能出现的小样本情况进行探究,提出了一个全新的结构,该结构将传统方法与机器学习方法巧妙结合,融合了分类能力强的人工特征与自编码器自动提取出的特征。然后,再利用特征选择算法对融合后特征进行自动选择,从而利用尽可能低维的特征表征原始信号。最后,使用分类器训练低维度特征,形成了小样本条件下通信信号分类新的解决方案,通过实验也验证了本文设计方案的可行性。但本文仍存在许多不足,比如本文算法对低信噪比条件下信号的识别率并无明显提升,这将作为下一步研究的重点。2.2 自编码器特征提取
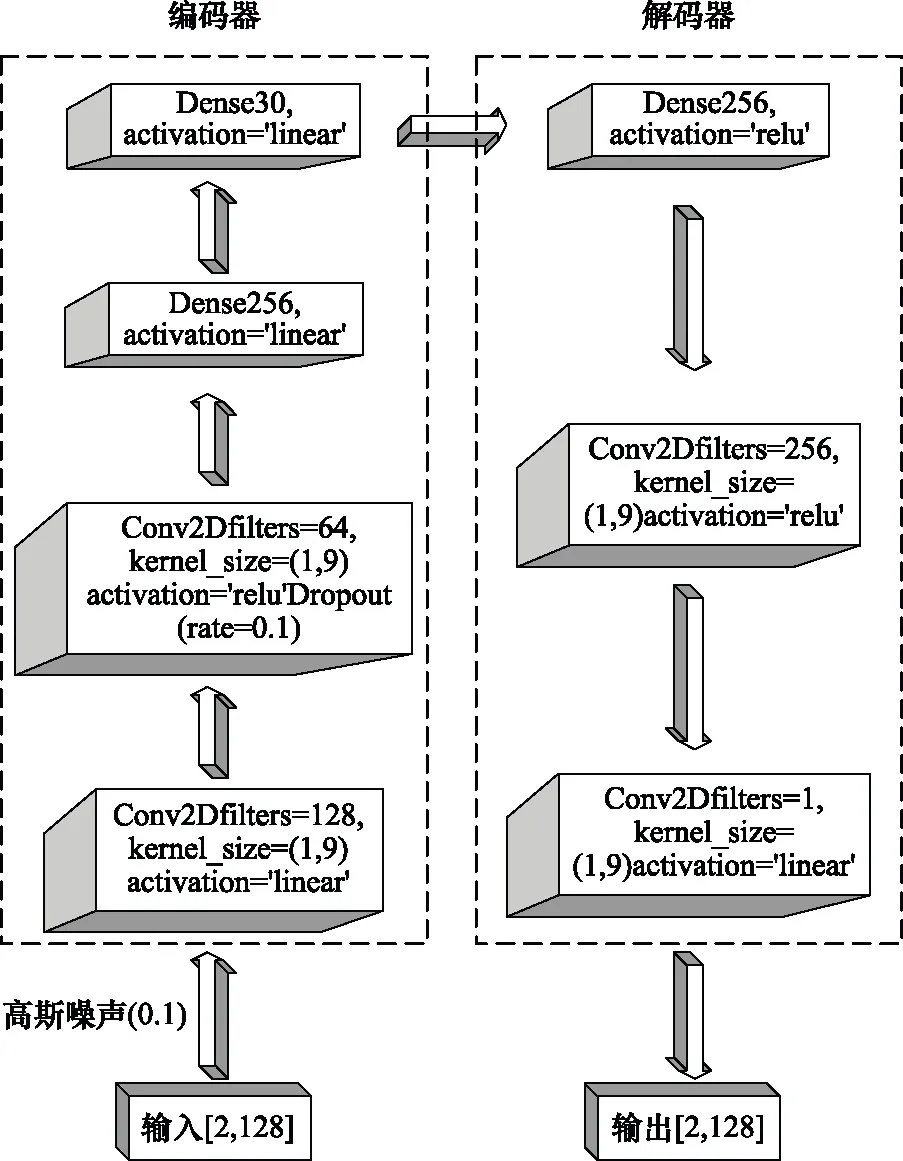
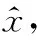
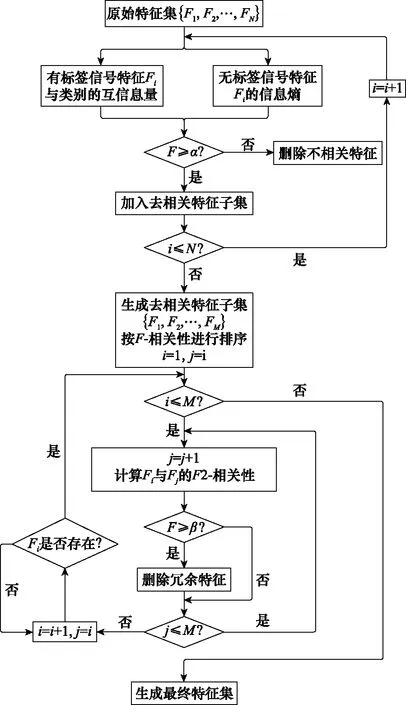
3 特征选择算法
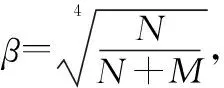
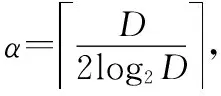
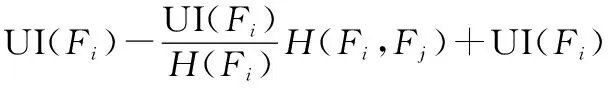
4 仿真验证
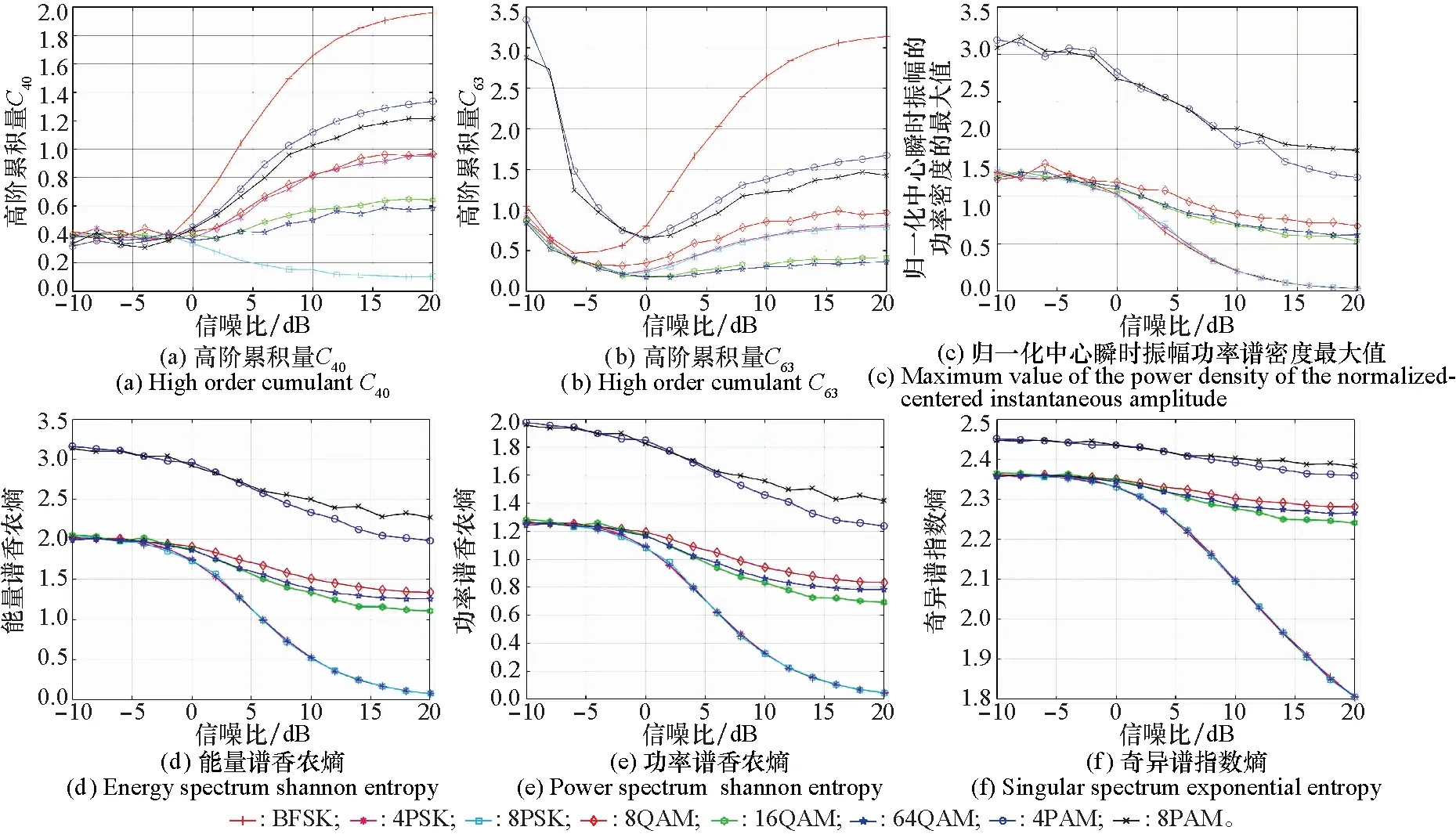
4.1 人工特征提取分析
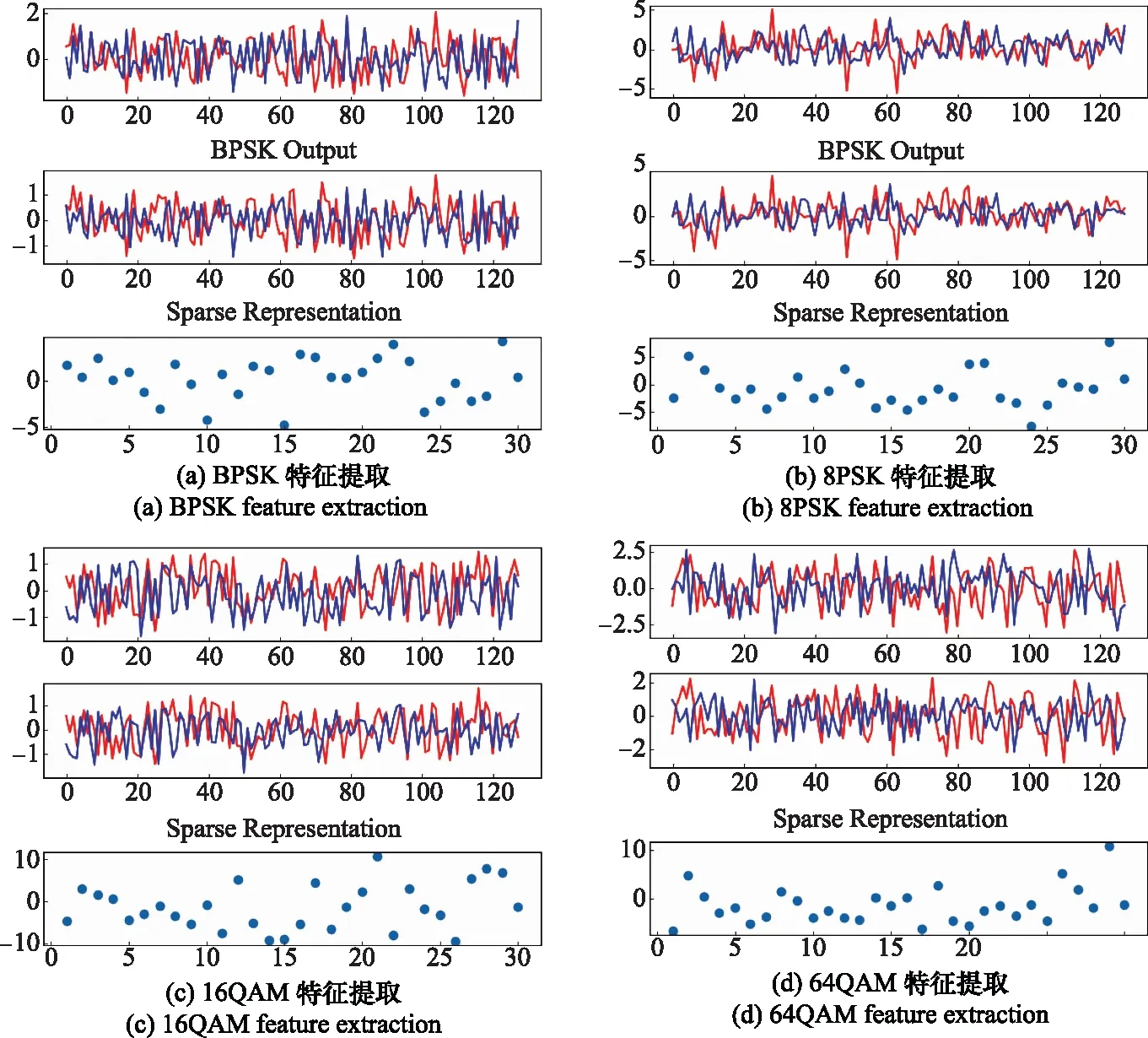
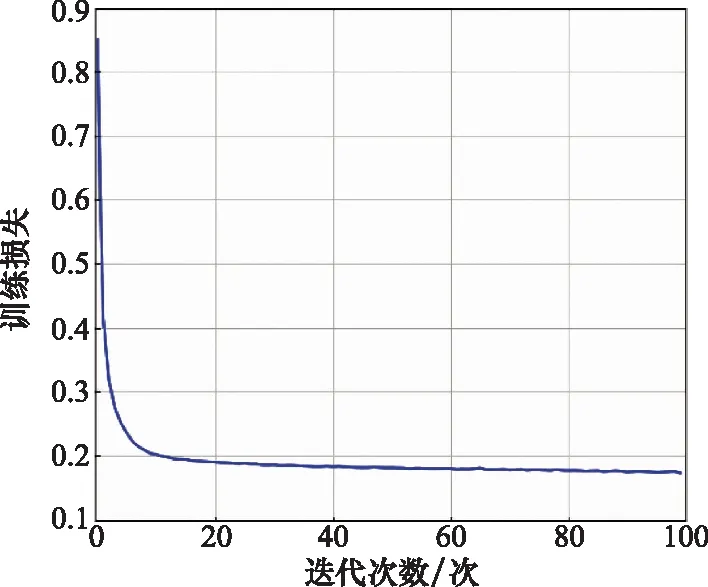
4.2 自编码器特征提取分析
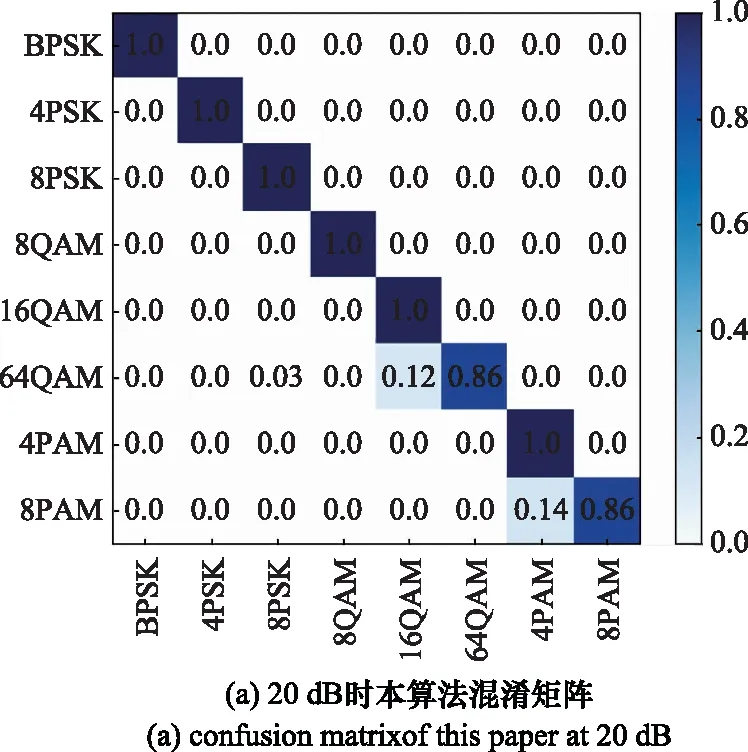
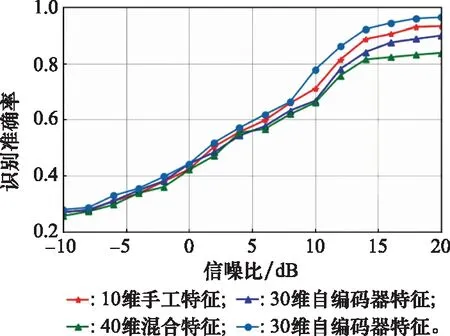
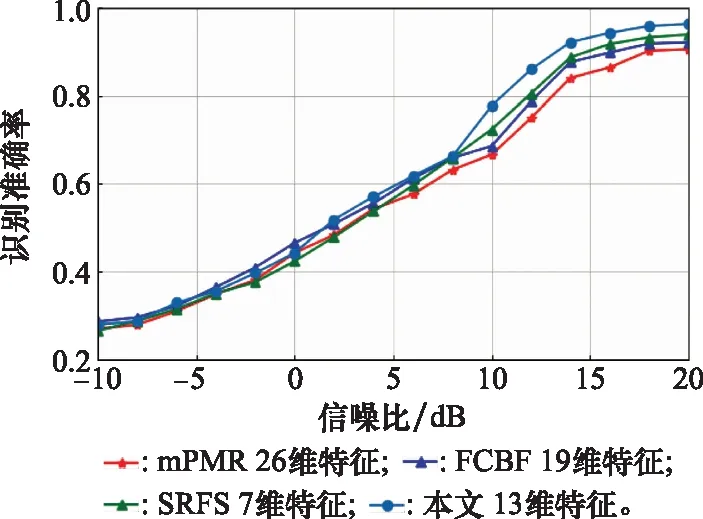
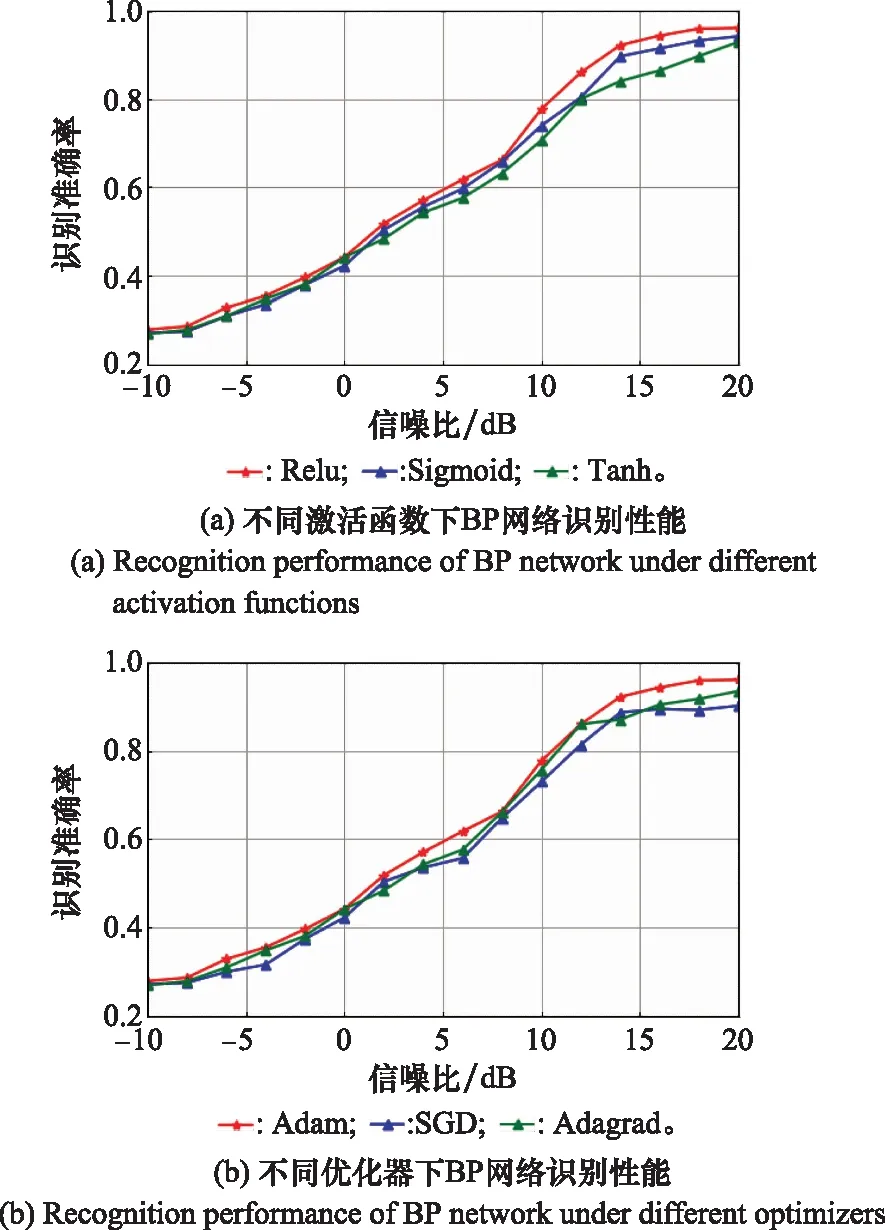
4.3 调制信号识别性能分析





5 结 论
