非寿险需求影响因素研究

欧阳汉 田秋红 廖文琪

(贵州财经大学大数据统计学院，贵州 贵阳 550025)

一、引言

2014年，国务院印发《关于加快发展现代保险服务业的若干意见》，指出保险是现代经济的重要产业和风险管理的基本手段，同时也是社会文明、经济发达程度、社会治理能力的重要标志。随着经济社会的快速发展，保险行业已经参与到国民经济的进程中，保险的社会“稳定器”和经济“助推器”作用将得到有效发挥。

寿险主要是对人的生命及身体健康进行保障，非寿险是对财产及责任利益进行保障。与寿险相比，非寿险的保障对象较广，不仅有人、物，还有责任等非实体，因此，非寿险的影响因素较多。学者对非寿险的影响因素进行研究，得到GDP(刘志雄，2005；罗皓等，2005；锁凌燕等，2005)、固定资产投资(张宗军，2011；张宗军，2012)有显著影响，部分学者指出社会因素中的受教育程度会产业显著影响(赵桂芹，2006；尚君等，2013)。Cavante等(2013)发现非寿险保费与国民经济有关系，国民经济的增长会促进非寿险发展。Hasan(2018)研究得到除利率外，其他宏观经济因素对非寿险公司绩效无显著影响。Shiu(2019)发现在英国得的非寿险需求主要影响因素是保险产品本身。

基于学者对非寿险需求的研究，本文将选用1988年～2018年中国的时间序列数据，对影响非寿险的因素进行实证研究。

二、指标选取及研究方法介绍

1.指标选取

选取国内生产增长率、固定资产增长率、总抚养比、风险水平、教育水平[14]作为解释变量，保费增长率为被解释变量，其中风险水平是以年度火灾、交通事故损失加总来表示，教育水平是以普通高中、高校毕业生人数加总来表示。本文实证分析的数据的时间序列长度为31，相关数据(1988-2018)来源于中国统计局官网、中国银行官网、《中国保险年鉴》得到。

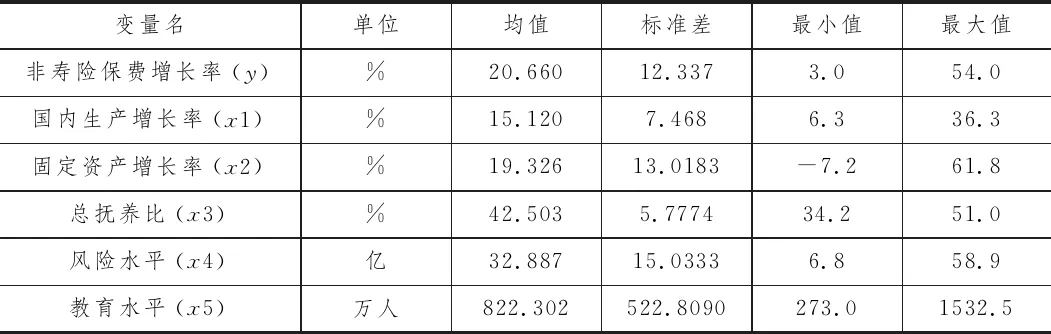
表1 变量的统计性描述

2.方法介绍

(1)平稳性检验

平稳性检验的方法主要有两种：第一种是根据时序图和自相关图的特点来判断其平稳性；第二种就是构建检验统计量，利用假设检验来判别平稳性(田行宇等，2018)，构造检验统计量的方法主要有单位根检验。

ADF单位根检验检验估计回归方程由三个模型完成：

其中t为时间变量，代表序列随时间变化的趋势。模型的检验原理同DF检验，即t检验；检验顺序为复杂到简单；三个模型全部检验通过才能证明该序列是平稳时间序列。

(2)基于协整和误差修正模型

对于k个时间序列Yt=(y1t,y2t,…ykt),，k维向量Yt的分量被称为d，b阶协整，记为Yt～(d,b)，即Yt的各个分量序列存在协整，如果满足如下条件：

Yt～I(d)，要求Yt的每个分量Ytt～I(d);

存在非零向量β，使得β，Yt～I(d-b),0≤b≤d;

Engle和Granger多个时间序列之间存在协整关系的基础上，构建了向量误差修正模型VECM，由于在向量误差修正模型中，一阶差分的使用消除了变量可能存在的趋势因素，从而避免了伪回归等问题，模型中的差分项可以使用t检验和F检验来选取，可以更好地对短期动态关系进行分析，向量误差修正模型的构建原理如方程所示。

这个方程可以用误差修正模型表示为：

式中αecmt-1=β，Yt-1是误差修正项，其系数α是反映调整的速度。

3.格兰杰因果关系检验

该检验方法是诺贝尔经济学奖得主克莱夫·格兰杰(CliveW.J.Granger)所开创，用于分析经济变量之间的格兰杰因果关系(梁宗经等，2020)。他给格兰杰因果关系的定义为“依赖于使用过去某些时点上所有信息的最佳最小二乘预测的方差。

其中残差序列u1i、u1k之间不相关，检验的原假设为：H0=β1=β2=…=βi=0，检验统计量为F统计量：

4.脉冲响应函数

脉冲响应函数是用来考虑扰动项的影响是怎么样从一个变量传播到另一个变量的，主要研究影响的传递过程，其主要的基本思路是通过对时间序列模型的分析来实现对向量间影响传递关系的实证分析，下面通过简单的脉冲响应函数来了解其基本思想。首先阐述下脉冲响应函数在两变量(htzt)的VAR(2)模型中的实现过程。

其中，a、b、c和d都是参数，扰动项以t的形式存在。

三、实证分析

1.平稳性检验

要进行时间序列分析，首先必须进行平稳性检验，其趋势如图1、图2所示，从图1变量趋势和图2变量的一阶差分趋势可以看出，所有变量x1、x3、x4、ln(x5)表现出来不平稳，而他们的一阶差分表现出平稳性。

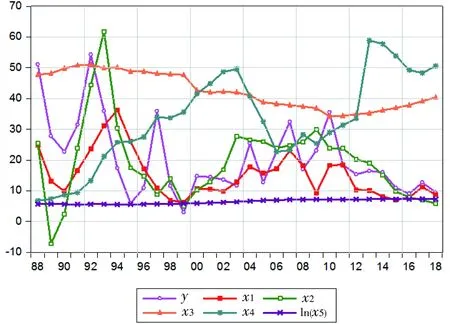
图1 变量时间趋势图

图2 变量一阶差分趋势

ADF检验如表所示，从表2单位根检验结果可以看出，一部分变量序列是平稳的，一部分变量一阶差分后在5%显著水平上都是平稳序列。

从表2可以看出序列y和序列x2平稳，x1、x3、x4、ln(x5)经过一阶差分后平稳，具有相同的单整阶数，符合进行协整检验的必要条件。

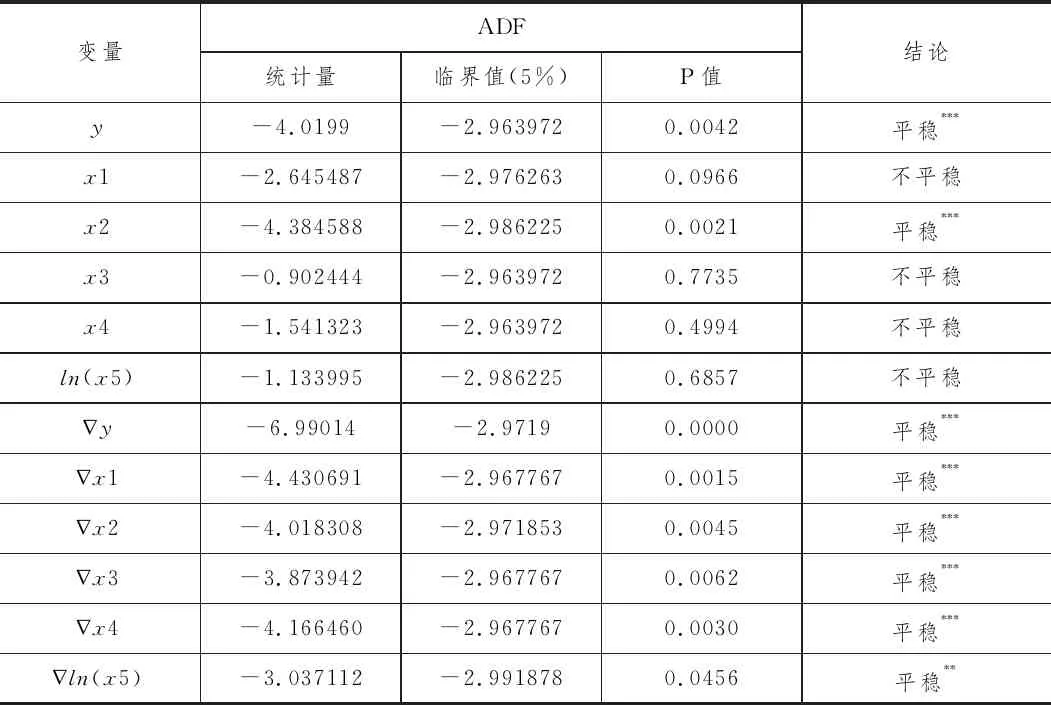
表2 各变量单位根检验

2.协整方程的建立

为了确定上述序列之间是否有长期稳定关系，是否能得到协整方程，本文将采用Johansen-Juselius协整检验法对序列的协整关系进行检验，同时在检验之前，还要确定VAR模型的最优滞后阶数，协整检验的滞后阶数等于相应的VAR模型的滞后阶数减1。可以根据AIC和SC最小信息可以确定VAR模型的最优滞后阶数。从信息准则可以看出，滞后阶数为3时，AIC和SC值最小，所以选择VAR模型的滞后阶数期为3。

VAR模型选择滞后阶数为3时效果满意，所以选择协整检验的滞后期为2。序列x1、x2、x3、x4、ln(x5)和y之间存在多组协整关系，根据最大向量特征值对应的向量得到标准化的协整方程，所以得到标准化的协整关系式为：

y=-0.7173*(x1)+0.3072*(x2)+0.3979*(x3)+3.1173*(x4)+23.0683*ln(x5)

(0.0956) (0.0512) (0.0270) (0.2593) (2.3114)

式中是将y作为被解释变量，将x1、x2、x3、x4、ln(x5)作为解释变量，括号内的为t统计量。

3. 向量误差修正模型(VECM)的建立

协整方程考虑到了序列的长期波动关系，并没有介绍各序列短期波动对于模型的影响，所以在此基础上，对协整模型进行补充，对具有协整关系的变量y、x1、x2、x3、x4、ln(x5)建立误差修正模型。其中y的误差修正模型公式如下：

▽y=-0.287▽yt-1-0.024▽yt-2-0.551▽(x1)t-1-0.252▽(x1)t-2+0.945▽(x2)t-1+0.315▽(x2)t-2+2.221▽(x3)t-1-3.759▽(x3)t-2-0.146▽(x4)t-1+0.030▽(x4)t-2-88.673▽ln(x5)t-1-98.51▽ln(x5)t-2-1.380vecmt-1+0.910

vecmt-1=-0.717*(x1)+0.307*(x2)+3.117*(x3)+0.398*(x4)+23.068*ln(x5)

根据向量误差修正模型可以看出，非寿险保险增长率会受到上一期、上二期非寿险保费增长率、国内生产增长率、固定资产增长率、总抚养比、风险水平、教育水平的短期波动影响，从各变量差分项滞后一、二期可以看出，短期上，非寿险保费增长率、国内生产增长率、固定资产增长率、总抚养比、风险水平、教育水平有不同的作用。

误差修正后可以看出方程拟合优度为0.81，调整拟合优度0.7，AIV(7.198)，SC(7.86)都较小：可以看出误差修正方程的残差序列平稳。说明方程效果较为满意。接下来将检验误差修正方程的残差，根据其ADF检验结果看出误差修正方程的残差序列平稳，说明方程效果较为满意。

4. 格兰杰因果关系检验

不管是传统模型还是协整模型，都只是给出了序列之间的方程式，揭示它们之间的关系，但并没有给出经济和理论意义的因果关系，即时谁引起谁的变化。为了给出这个问题的答案，且Granger因果检验法对序列的因果关系进行检验，且Granger因果检验法的前提是各序列必须是平稳的。利用Eviews软件在误差修正模型的基础上检验Granger因果关系。

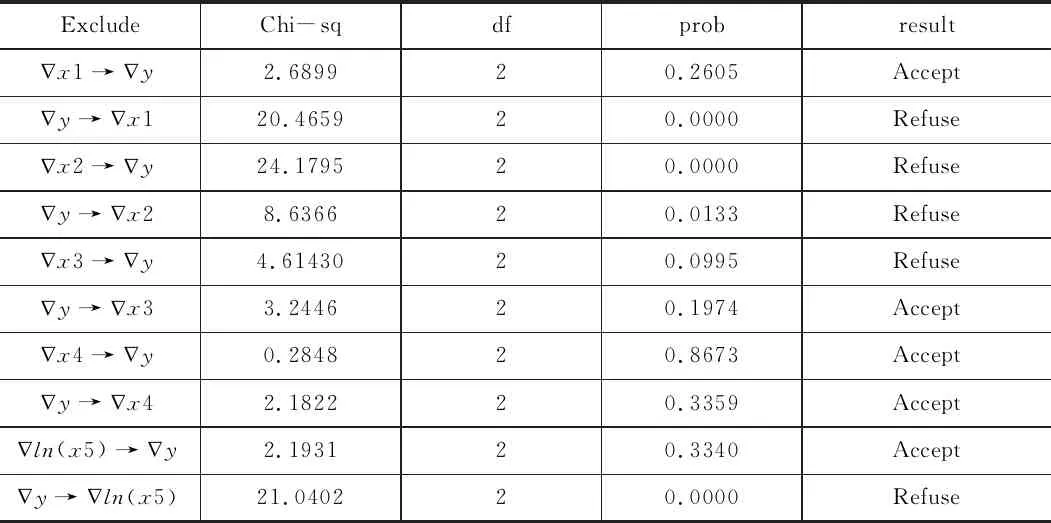
表3 Granger因果检验结果

从表 2可以看出，非寿险保费增长率是引起国内生产总值增长率变化的短期原因，固定资产增长率和非寿险保费增长率之间存在短期因果关系，总抚养比变化是引起非寿险保费增长率变化的短期原因，非寿险保费增长率是引起教育水平对数变化的短期原因。

5. 脉冲响应函数分析

基于VECM模型的脉冲响应函数的脉冲响应图，分析影响因素对非寿险保费增长率冲击的短期动态效应，各影响因素对非寿险保费增长率在15期内的脉冲冲击响应结果如图3所示。实线部分为脉冲响应函数值随时间变化的路径，说明了各非寿险保费增长率影响因素对非寿险保费增长率冲击强度大小的变化过程。

图3 脉冲响应函数分析结果

从图3中可以看出，国内生产增长率在第1期时，国内生产增长率对非寿险保费增长率的响应值为0，小幅度波动后在第3期时达到最高点，随后有微小的负向作用。

当给固定资产增长率一个正向冲击后，在第2期响应为正且达到最大值，为5.9932，然后在第4期为负且降低到最小值，为-2.7520，在第5期时后呈现正向冲击，逐渐趋于稳定状态。说明固定资产增长率对非寿险保费增长率有一定的影响作用，从长期来看，固定资产增长率会促进经济发展，有利于非寿险保费增长率的提高。

当给总抚养比一个正向冲击时，会给非寿险保费增长率带来负向的冲击，从第1期开始一直为负且持续降低在第15期达到最大值，为-5.6104，表明短期内总抚养比的正向冲击对非寿险保费增长率具有一定的作用。说明总抚养比短期内由于老龄化程度加重，有利于非寿险保费增长率的提高，但随着年龄结构的不断变化，总抚养比随之増大，对非寿险保费增长率起到了一定的阻碍作用。

给风险水平一个正向冲击，对非寿险保费增长率变化量的影响始终为负，且从整体上来看整体降低。即风险水平程度受到冲击后，给非寿险保费增长率带来反向冲击，并在第9期达到最小值，为-3.5378，表明短期内风险水平程度的正向冲击对非寿险保费增长会生暂时的阻碍作用。说明中国火灾损失和交通事故损失的增加，这对非寿险保费增的提高是不利的。

给教育水平一个正向冲击后，对非寿险保费增长率变化量的影响整体为正，在第2、3期时，教育水平对非寿险保费增长率变化量的影响为负，表明短期内教育水平程度的正向冲击对非寿险保费增长会生暂时的阻碍作用。然后对非寿险保费增长率变化量的影响为正且稳定，长期来看，教育水平对非寿险保费增长率有促进作用。

四、结论与展望

本文选取国内生产增长率、固定资产增长率、总抚养比、风险水平、教育水平五个主要因素作为解释变量，保费增长率为被解释变量，利用协整模型，分析序列的平稳性，并且考虑了序列间的长期波动关系，然后对协整模型进行误差修正，消除序列短期波动的影响。最后进行序列之间的Granger因果检验、脉冲响应函数，主要结果如下。

通过协整检验可知，非寿险保费增长率与国内生产增长率、固定资产增长率、总抚养比、风险水平、教育水平存在显著的长期均衡关系，这种关系表明，在长期上，固定资产增长率、总抚养比、风险水平、教育水平对非寿险保费增长率均有正向影响，而国内生产增长率对非寿险保费增长率有负向影响，从影响程度来看，教育水平影响最大，其次是风险水平，而固定资产增长率的影响最小。

向量误差修正模型表明，非寿险保费增长率受到上期非寿险保费增长率、国内生产增长率、固定资产增长率、总抚养比、风险水平、教育水平的短期波动的影响。固定资产增长率、总抚养比滞后一期的变化对本期非寿险保费增长率有正向影响，而非寿险保费增长率、国内生产增长率、风险水平、教育水平对本期非寿险保费增长率具有反向影响。其中教育水平的影响程度相对于其它变量来说较为突出。

基于向量误差修正模型，得到序列之间的短期因果关系，固定资产增长率与非寿险需求互相显著影响，总抚养比正向影响非寿险需求，国内生产增长率、教育水平、风险水平不是影响非寿险需求的主要因素。

基于向量误差修正模型，采用脉冲响应函数对各个影响变量的变动对非寿险保费增长率的影响进行了分析，短期内，国内生产增长率、固定资产增长率、教育水平受到正向冲击后，对未来一段时间非寿险保费增长率均产生稳定的积极影响，其中固定资产增长率对非寿险保费增长率的波动最为敏感。

最后，国家发展固定资产投资可以促进非寿险行业的发展，同时大力宣传非寿险的风险转移和理财功能，让居民了解非寿险，并可以正确购买保险产品，发挥非寿险的积极作用。另外，非寿险行业需要不断的创新和改革，让非寿险产品发挥作用。