基于随机流网络与Markov过程的制造系统可靠性建模及维护优化

高英铭，陈 震，张秀芳，潘尔顺

(上海交通大学 机械与动力工程学院，上海 200240)

随着科技进步和经济发展，制造系统结构日趋复杂，企业间的竞争愈发激烈，对制造系统可靠性的要求也越来越高.制造系统可靠性是制造过程平稳进行、提高生产效率的重要保障，也是企业重要的竞争优势所在.目前，对制造系统可靠性的评价主要分为两类[1]：一类是对传统单一设备可靠性定义的扩充，即制造系统在规定时间内正常运行的概率[2-3]；另一类是从制造系统任务可靠性的角度，即制造系统在规定时间内，完成的合格成品数量大于客户需求数量的概率[4-5].

许多学者沿用传统的可靠性定义来评估制造系统可靠性.何益海等[6]提出一种考虑产品质量的系统可靠性评价方法，将系统可靠性视为系统未失效和产品质量合格两者概率的乘积，其中产品质量与设备刀具和夹具的磨损情况存在耦合效应，进而影响系统的失效概率.刘银华等[7]在夹具磨损的基础上，考虑来料偏差和定位时的配合公差，对车身装配系统可靠性进行评价.杜世昌等[8]对制造系统中产品尺寸偏差的累积与传递效应进行建模，从系统层面控制尺寸偏差.Liu等[9]针对不可修复系统，建立非齐次Markov模型，分析多态系统性能的衰退过程.在此基础上，周丰旭等[10]结合通用发生函数和模糊层次分析法分析非串联多级制造系统的可靠性.Sharma等[11]结合故障树分析(FTA)和失效模式及后果分析(FMEA)从定性和定量两个方面分析复杂机电系统的可靠性.

同时，有许多学者认为任务可靠性更加适合用于制造系统的可靠性评价.Lin等[12]认为基于网络模型分析系统的产能十分适用于制造系统的可靠性评估.Tina等[13]对离散的随机流网络系统进行分析，以输出量作为指标进行可靠性建模，并提出Song Rule对模型进行简化求解.Chang等[14]考虑设备间的联合缓存，采用仿真方法随机生成容量状态，并通过敏感性分析确定最可能增加缓冲区容量的位置.Gu等[15]考虑材料及机器的动态变化，基于随机流网络对不同参数下的制造系统进行了数值分析.

以上学者在系统可靠性评估中，未考虑设备退化对系统可靠性的影响，因此无法全面反映不同阶段制造系统的状态.综合分析制造系统可靠性与各设备退化及维护的关系，将维护优化从设备层扩展到系统层，有利于减少设备的不必要维护，在保障系统可靠性的同时，最小化维护成本.

针对现有研究的不足，本文以多工位流水线制造系统为研究对象，考虑产品返工情况，以任务可靠性作为制造系统可靠性的评价指标，运用随机流网络模型对系统可靠性进行建模，并基于Markov方法对设备状态进行转换建模，以平稳状态下系统维护的平均总成本最低为目标，对系统的维护方案进行决策.

1 制造系统可靠性评价

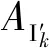
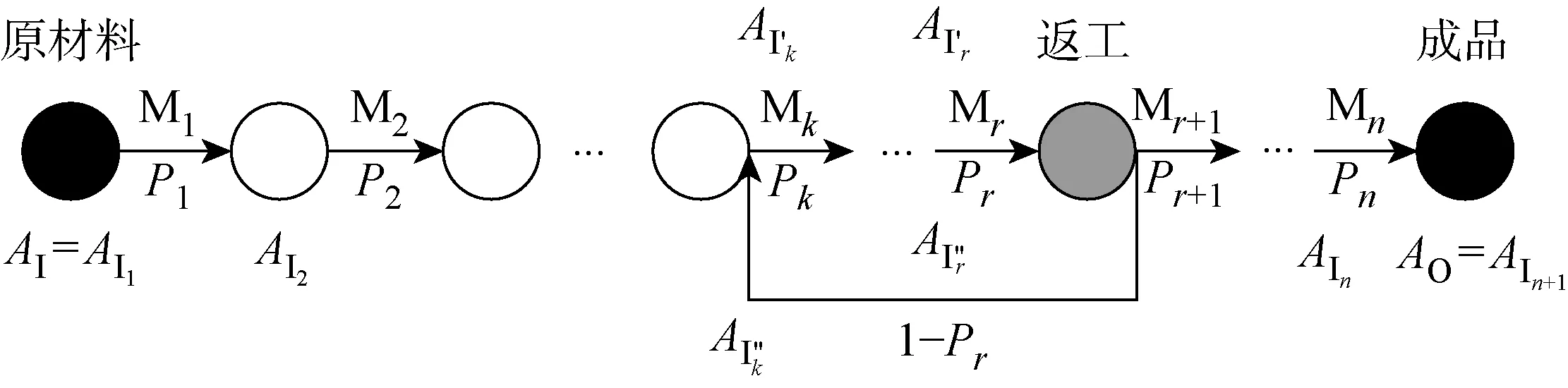
图1 制造系统网络结构Fig.1 Structure of manufacturing system network

原材料依次在设备M1～Mn上加工变为成品，其中，设备Mr后的检查点是一个返工检查点，即设备Mr制造出的不良品将回到设备Mk进行返工.因此，对于给定的产量需求量AD，制造系统的可靠性可以用规定时间内系统输出满足需求的概率来表示

R=P(AO≥AD)

(1)

假设条件如下：① 产品各工序加工时间相同；② 每个产品最多返工一次；③ 不考虑设备的计划停工时间；④ 原材料供给充足；⑤ 制造系统网络为一个连续流网络；⑥ 设备状态间的转换是一个齐次Markov过程，即每个状态转换至其他状态的速率只与该状态本身有关；⑦ 设备维护只能由较劣状态向较优状态维护，不会维护至更劣状态，且设备处于故障状态时必须维护.

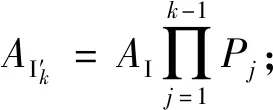
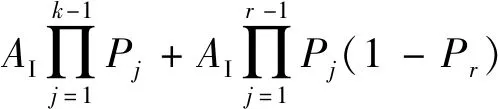
(2)

同理，可计算出在设备Mk后的各个设备的输入.综上，任意设备Mi的输入可以通过下式计算：

AIi=

(3)

若系统输出满足需求，则AO≥AD.其中，系统输出可以认为是虚拟设备Mn+1的输入，即AO=AIn+1，故有如下公式：

(4)

(5)

从而，可以获得满足系统需求的设备Mi的最小输入可以表示为

(6)

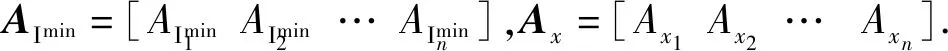
R=P(AO≥AD)=P(Ax≥AImin)=

(7)

2 制造系统维护策略

2.1 系统维护模型建立

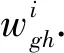
πiQi=0

(8)

式中：0=[00…0]，且

(9)

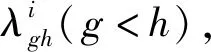
(10)

(11)

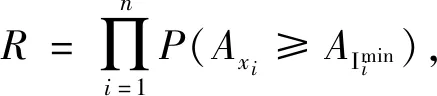
(12)

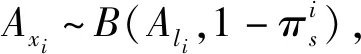
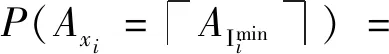
P(Axi=AImini)=

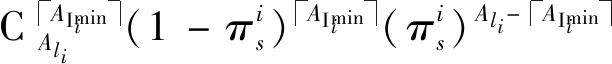
CAIminiAli(1-πis)AImini(πis)Ali-AImini

(13)

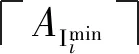
AImini

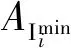
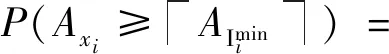
P(Axi≥AImini)=

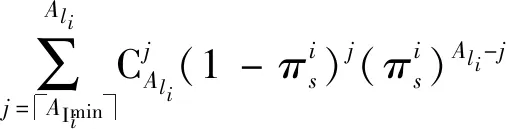
∑Alij=AIminiCjAli(1-πis)j(πis)Ali-j

(14)

所以制造系统可靠性满足下式：

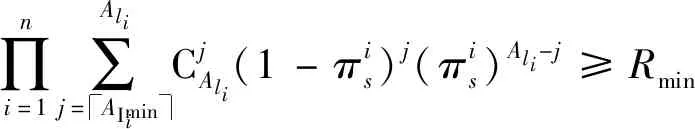
∏ni=1∑Alij=AIminiCjAli(1-πis)j(πis)Ali-j≥Rmin

(15)

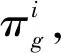
(16)

约束条件为式(3)、(6)、(8)～(11)、(15).

2.2 模型变换

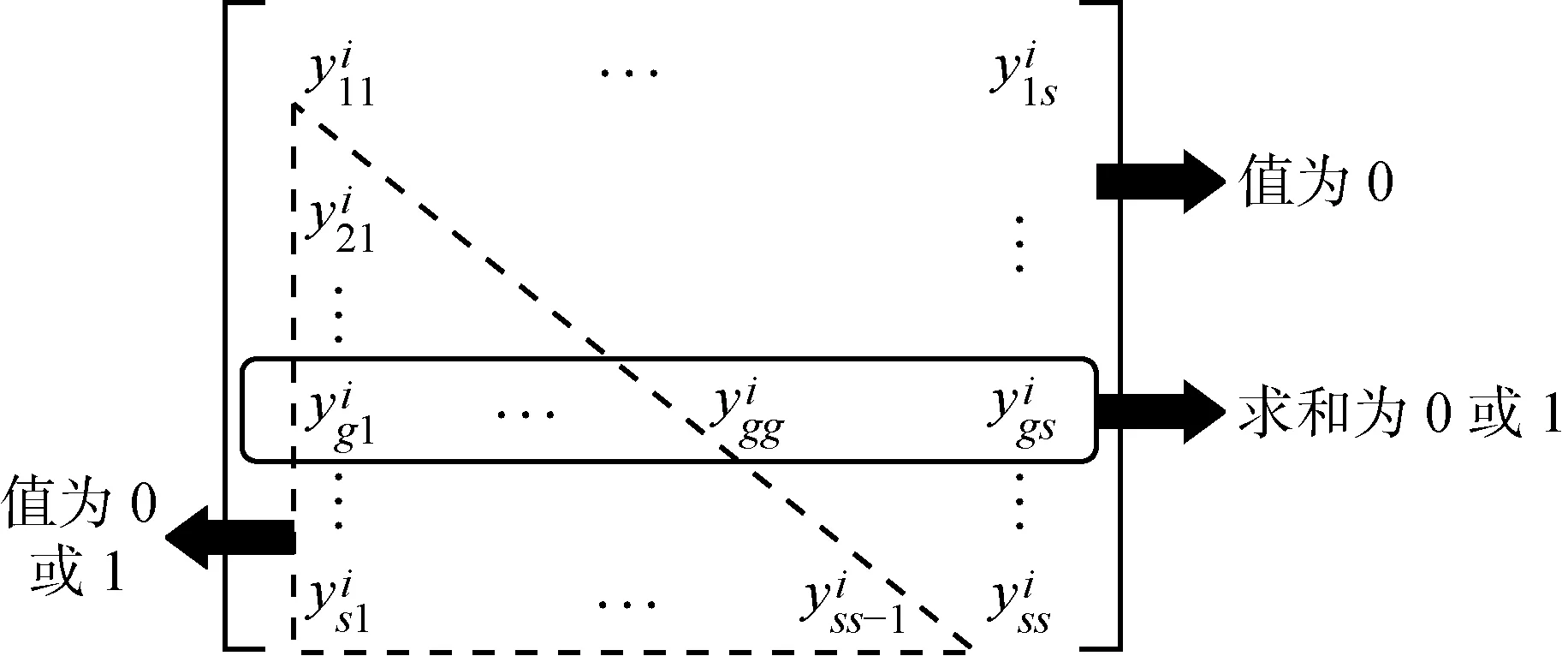
图2 决策变量矩阵Yi的形式Fig.2 Form of decision variable matrix Yi

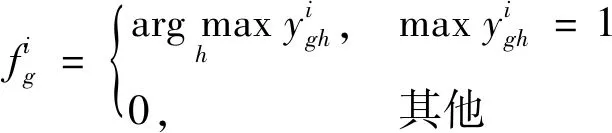
(17)

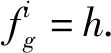
(18)

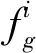
模型的计算过程为

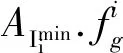
(3) 通过式(8)～(10)，计算转移速率矩阵Qi和平稳分布πi.

(4) 通过式(15)，计算系统可靠性并将其与给定的可靠性阈值比较.

(5) 通过式(16)，计算维护成本.

3 算例分析

下面通过算例分析来验证模型的有效性.制造系统由3种设备组成，每种设备有5台，每台设备的退化过程中包括状态1～4，共4种状态.状态1代表设备全新，状态4代表设备故障.原材料在3种设备上依次加工变为成品.每种设备加工出合格品的概率均为0.95.系统单位时间的输出需求量为3个，系统可靠度最低要求为95%.设备的状态变化为齐次Markov过程.制造系统结构示意图如图3所示.

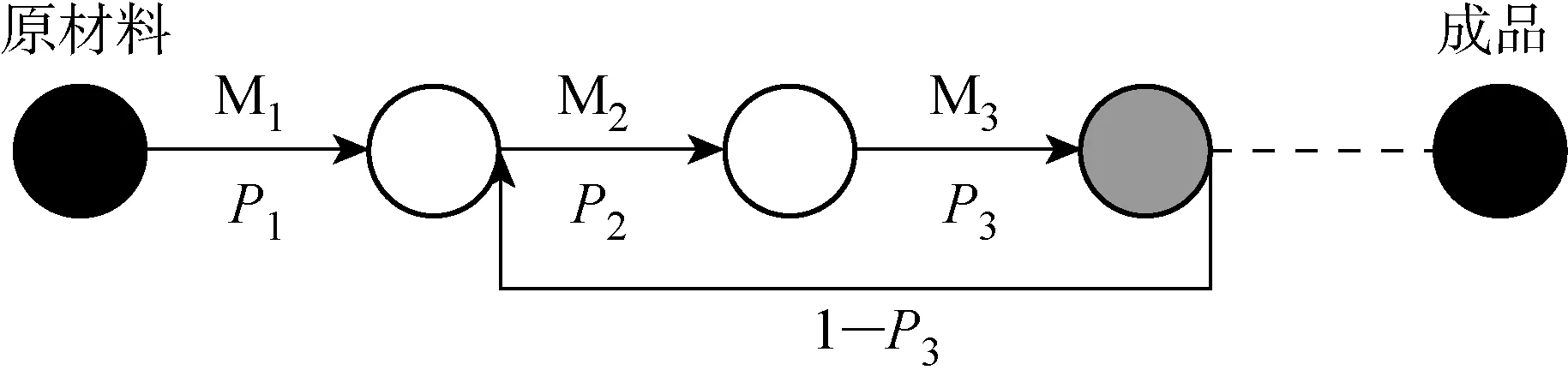
图3 制造系统结构示意图Fig.3 Diagram of manufacturing system structure

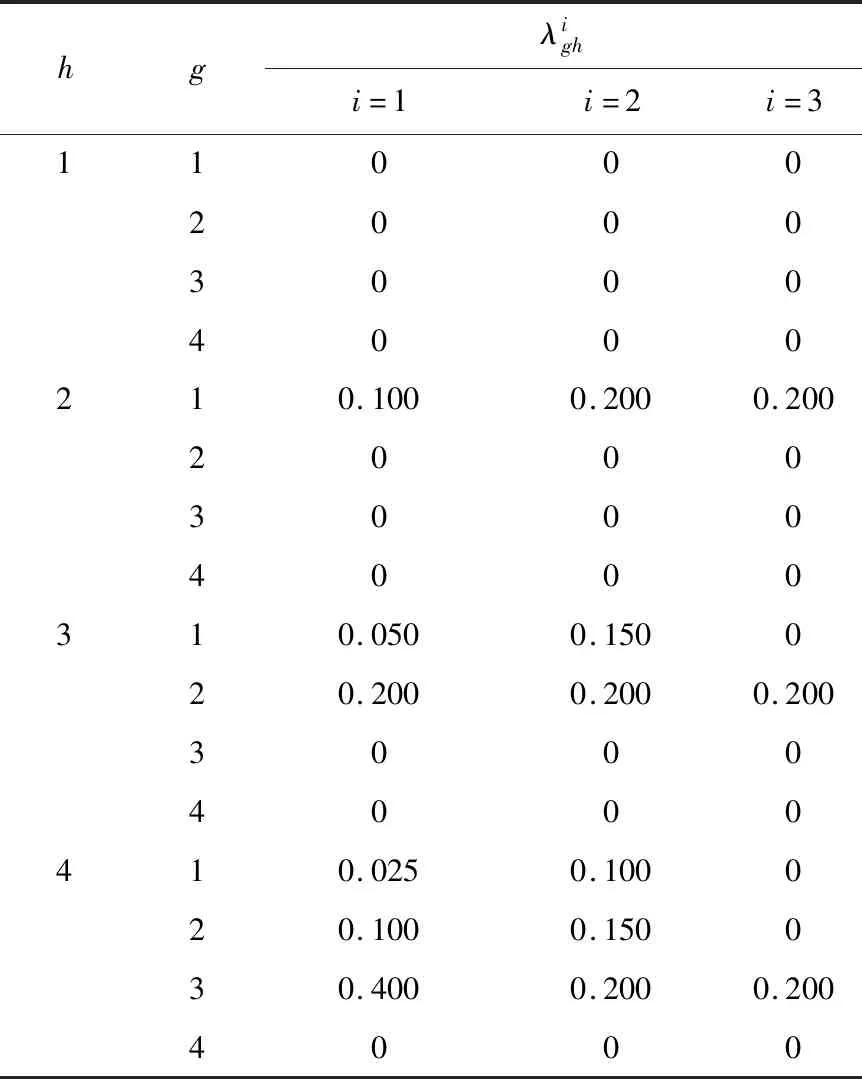
表1 退化过程中设备的状态转移速率Tab.1 State transition rate of devices during degradation

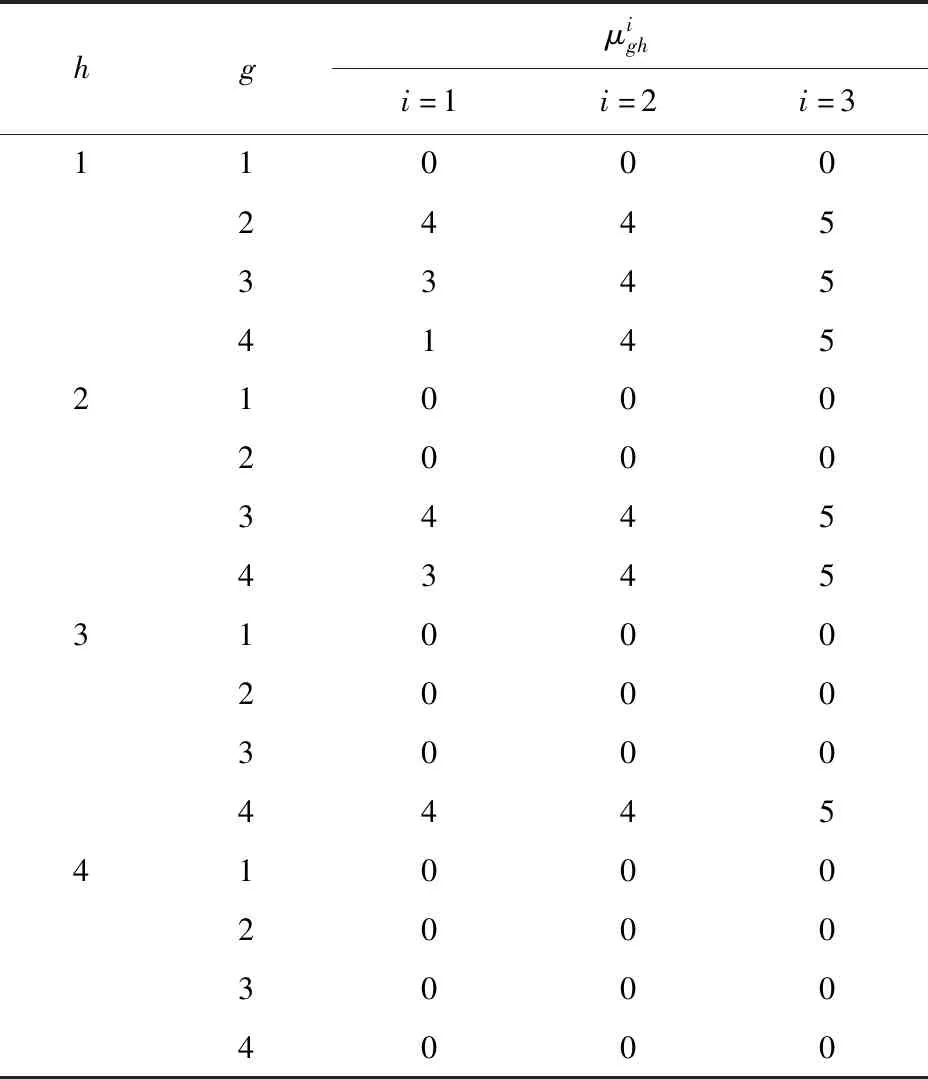
表2 维护过程中设备的状态转移速率Tab.2 State transition rate of devices during maintenance

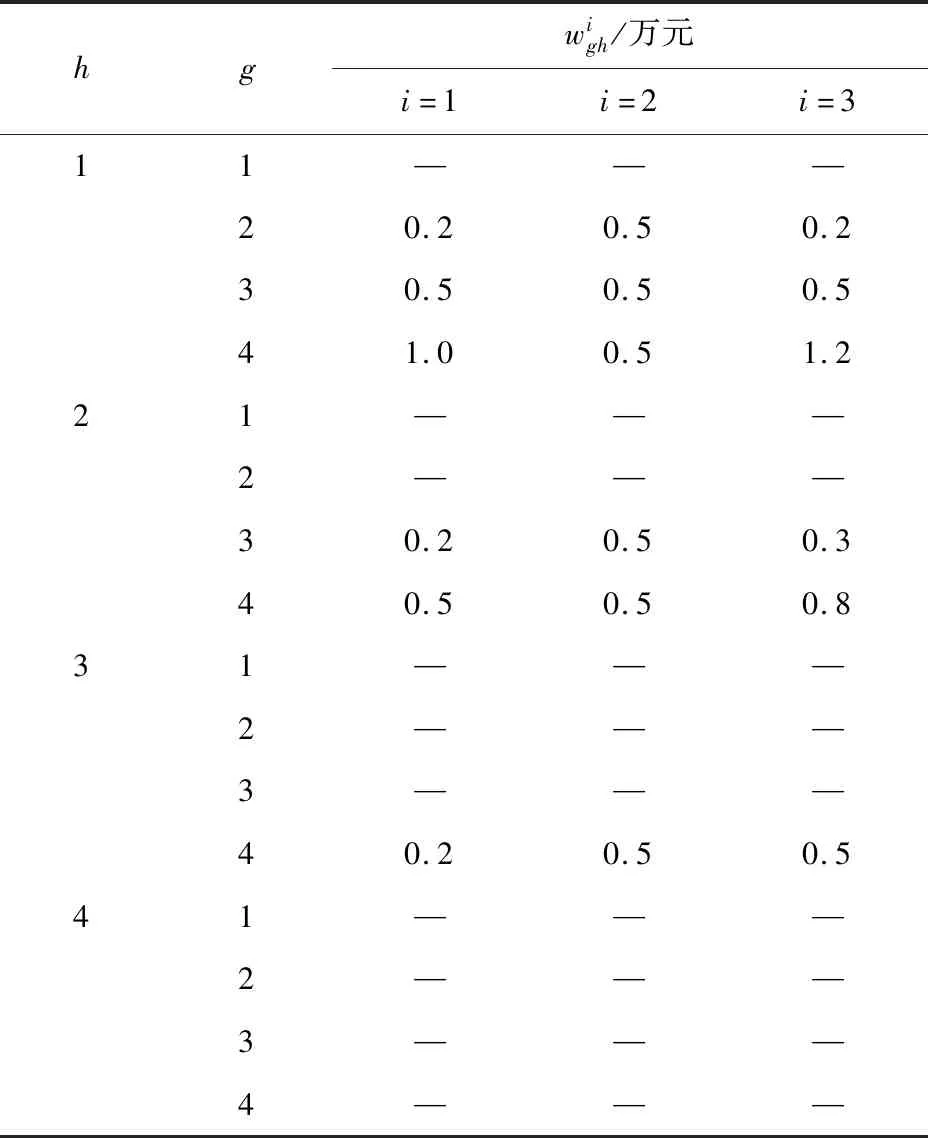
表3 设备各状态间的维护成本Tab.3 Maintenance cost among states of devices

计算步骤如下.

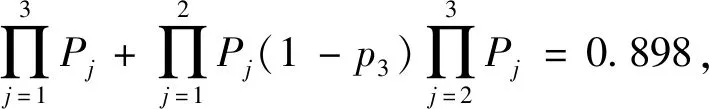
步骤1初始化g=4，gg=Ni.

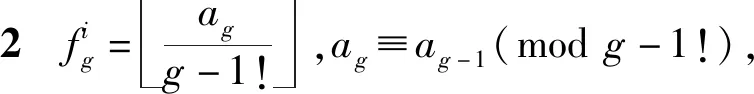
2 fig=agg-1!,ag≡ag-1(modg-1!),

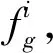
步骤3g=g-1.

步骤4若g≥1，返回步骤2；否则，计算结束.

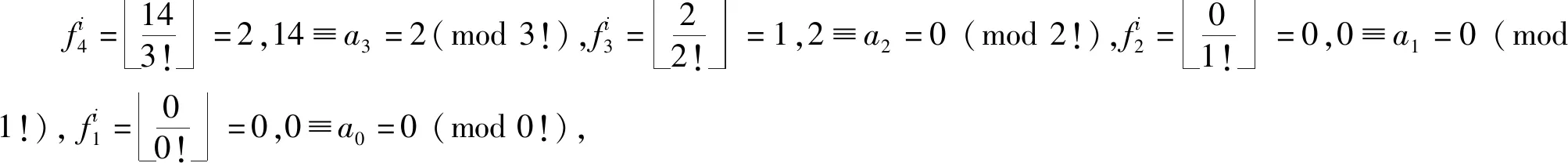
fi4=143!=2,14≡a3=2(mod3!),fi3=22!=1,2≡a2=0(mod2!),fi2=01!=0,0≡a1=0(mod1!),fi1=00!=0,0≡a0=0(mod0!),

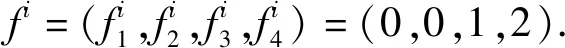
然后变化i，建立f=(f1,f2,f3)与正整数N的对应关系.通过上述步骤可以确定，对于每个i，正整数Ni的最大值为 4!-1=23.按照如下步骤建立f与正整数N的一一对应关系.

步骤1初始化i=3,bi=N.

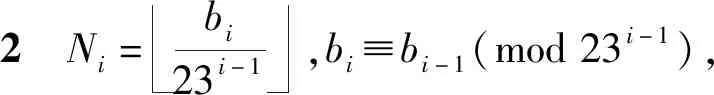
2 Ni=bi23i-1,bi≡bi-1(mod23i-1),

步骤即令bi除以23i-1的商为Ni，余数为bi-1.

步骤3i=i-1.

步骤4若i≥1，返回步骤2；否则，计算结束.

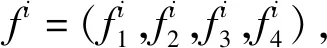
(4) 通过式(15)，计算系统可靠性并与给定可靠性阈值比较.

(5) 对于满足可靠性阈值的一组解，通过式(16)计算其维护成本，并与当前最小维护成本进行对比，以确定是否更新最优解.若N>(s!)n，计算结束；否则，令N=N+1，返回步骤(2).

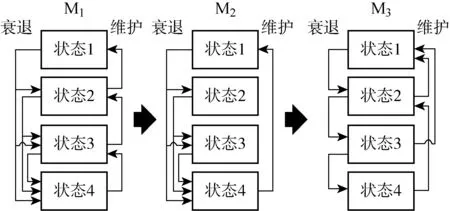
图4 最优维护方案示意图Fig.4 Diagram of optimal maintenance policy

下面对模型的计算结果进行分析.设备M1的维护方案为维护至相邻的更优状态；设备M2的维护方案为故障后维护至全新状态；设备M3的维护方案为若设备处于状态2、3，直接维护至状态1，若设备处于状态4，维护至状态2.由表2和3可知，设备M1的相邻状态间维护成本低、维护时间短，适合维护至相邻状态.设备M2不同状态间的维护成本和维护时间分布相同，适合故障后换新.设备M3相邻状态间的维护成本低，但是不同状态间的维护时间分布相同.由此可见，由模型获得的维护方案比较合理.

为了说明本文模型的有效性，将模型的求解结果与其他11种维护策略进行比较.将本文模型作为维护策略1(S1)；S2：故障后完美维护，即设备故障(状态4)后维护至全新状态(状态1)，其他情况不维护；S3：最小修，即设备故障后维护至故障发生前的状态，其他情况不维护；S4：设备故障(状态4)后维护至状态1，且设备衰退至状态2时维护至状态1；S5：设备故障(状态4)后维护至状态1，且设备衰退至状态3时维护至状态1；S6：设备故障(状态4)后维护至状态1，且设备衰退至状态3时维护至状态2；S7：设备故障(状态4)后维护至状态2，且设备衰退至状态2时维护至状态1；S8：设备故障(状态4)后维护至状态2，且设备衰退至状态3时维护至状态1；S9：设备故障(状态4)后维护至状态2，且设备衰退至状态3时维护至状态2；S10：设备故障(状态4)后维护至状态3，且设备衰退至状态2时维护至状态1；S11：设备故障(状态4)后维护至状态3，且设备衰退至状态3时维护至状态1；S12：设备故障(状态4)后维护至状态3，且设备衰退至状态3时维护至状态2.包括本文模型在内的12种维护策略对比结果如表4所示.其中：Ri为设备Mi的可靠性；wtot为系统级的维护成本.

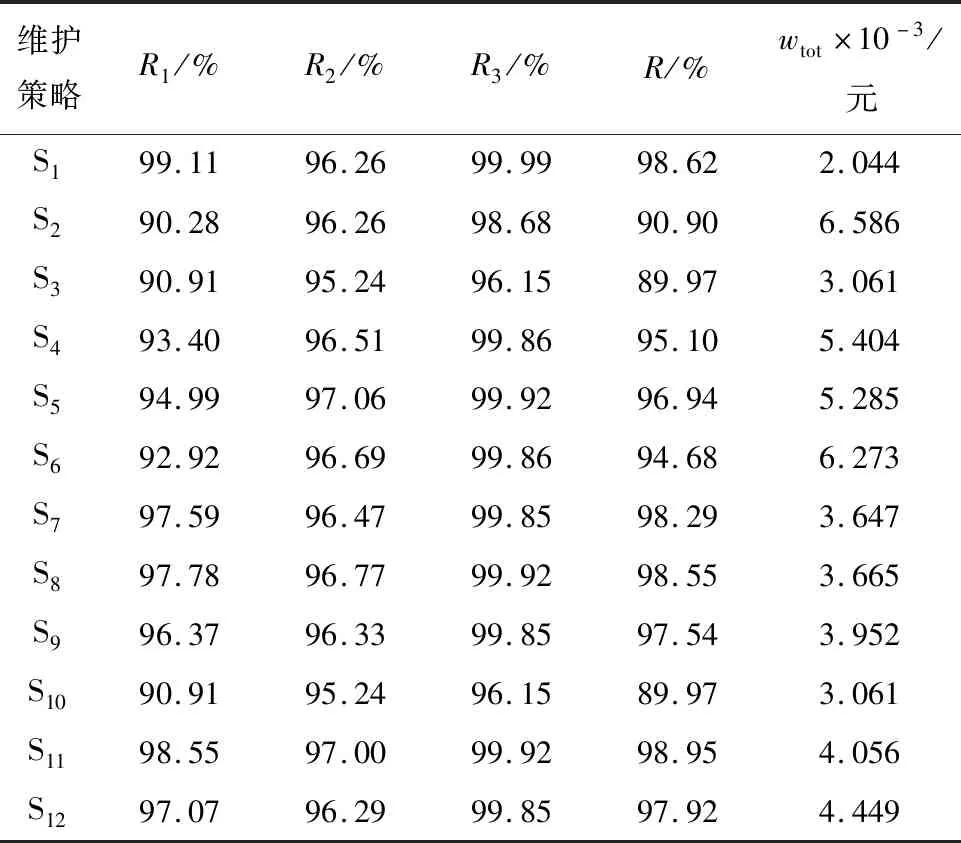
表4 不同维护策略的结果对比Tab.4 Comparison results of different maintenance strategies

12种维护策略的系统可靠性与维护成本之间的关系如图5所示.其中:-ln(1-R)用于衡量系统可靠性；Δwtot为Su与S1的维护成本差值；蓝色虚线为S1的系统可靠性.

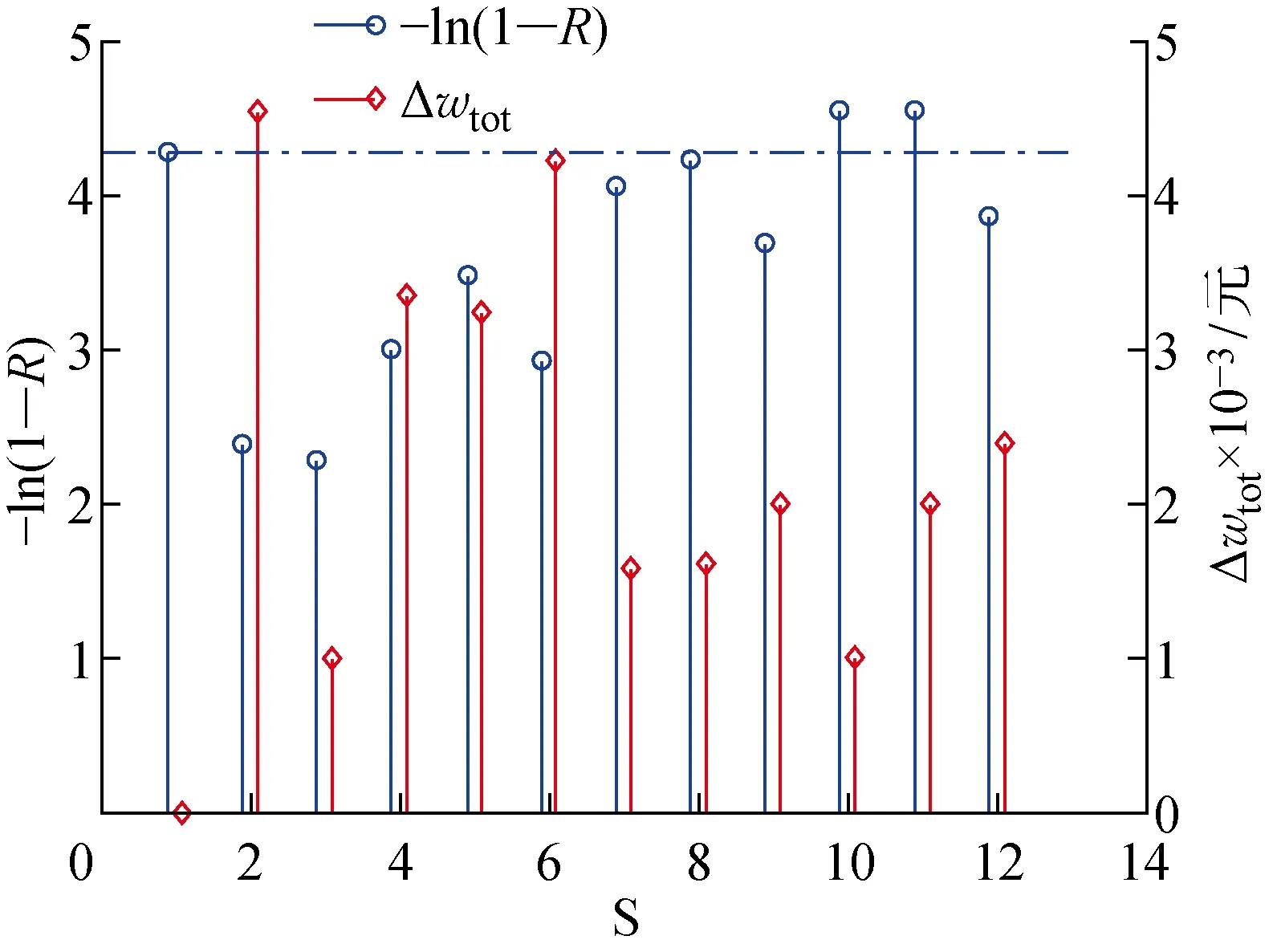
图5 不同维护策略的系统可靠性与维护成本Fig.5 System reliability and maintenance costs of different maintenance strategies

由表4可知，S1与其他维护策略相比，在系统可靠性方面最多可提高8.65%，在维护成本方面最多可降低68.96%.由图5可知，由于S1考虑了在设备退化至故障状态前进行先行维护，设备故障率更低，系统可靠性在所有维护策略中仅次于S11，并且两者相差较小.但在维护成本方面，S1系统地优化了各设备的维护策略，在保障系统可靠性要求的基础上，避免了设备的不必要维护，与其他策略相比S1的维护成本显著降低.

4 结语

本文在现有研究的基础上，考虑加工过程中产生的不良品以及不良品返工的情况，分析了系统中各设备的输入与系统输出的关系，建立了基于随机流网络的制造系统可靠性模型.同时，考虑到现有研究的不足，将制造系统可靠性大于等于给定阈值作为约束条件，建立了基于齐次Markov过程的系统维护模型.针对系统维护模型解空间过大的情况，提出一种模型变换方法，有效降低解空间规模.最后通过算例，证明模型结果与其他11种维护策略相比，维护成本更小，系统可靠性更高，证明了模型的有效性和先进性.