考虑相变诱导塑性的埋弧堆焊过程数值模拟方法研究

黄庆春，李昌，张大成，高鹤芯，韩兴，李云飞

（1.辽宁科技大学 机械工程与自动化学院，辽宁 鞍山 114051；2.中国能建东电一公司 锅炉项目部，沈阳 110179）

热轧辊是板带钢轧制生产的关键部件，其工作环境非常恶劣，承受交变应力作用，同时经历急热急冷过程，易发生热疲劳或过度磨损而报废。修旧轧辊一般通过堆焊方式恢复其原形状和尺寸，并赋予其更高的力学性能[1-3]。埋弧堆焊是通过电弧将堆焊材料熔化并与基体形成新的冶金结合，极大地提高了焊件的硬度、耐腐蚀性和耐磨性。堆焊中，基体和堆焊层因散热不同，引起温度差异而产生热应力，同时焊缝金属发生相变，组织转变引起体积变化而产生应力和变形，即转换诱导塑性（TRIP）。在这些力的综合作用下，焊件发生相变塑性应力与变形[5-7]。堆焊过程中局部加热及冷却会在焊缝中心产生残余拉应力，残余拉应力会促使裂纹缺陷处发生脆性断裂，降低堆焊层性能。因此，在实际生产中需尽可能地减少应力产生。

2009年，上海交通大学的刘俊䶮[8]建立9Cr1Mo钢管温度-组织-应力耦合的焊接三维模型，计算了焊接中马氏体相变随热源移动的变化，并对焊接残余应力的轴向分布进行预测。2001 年王文先[9]使用低相变点焊条进行焊接实验，发现基体冷却中焊缝金属发生马氏体相变，相变体积膨胀会降低焊接热场造成的残余拉应力，甚至出现残余压应力，从而提高焊接疲劳强度。2012 年，周野飞[10]建立了堆焊应力场模型，对热轧辊堆焊冷却过程中发生的马氏体相变应力进行了数值模拟。马氏体相变引起的体积变化有助于减小堆焊热影响区的残余应力。2016 年，邓德安[11]基于SYSWELD 软件模拟了P92 焊接接头温度场及应力场分布，考虑了固态相变引起的体积、屈服强度变化及相变塑性（TRIP）对焊接残余应力的影响。2017年，王学等人[12]利用ABAQUS 分析了马氏体相变对Cr 钢焊接接头环向、轴向应力演化的影响，发现低温下马氏体相变不仅抵消了焊缝和热影响区热收缩所形成的拉应力，且形成了显著的压应力。2019 年，Hu Z X 等人[13]采用ABAQUS 和其子程序，考虑了马氏体相变潜热对温度的影响，以及体积膨胀、屈服强度变化和变形塑性对应力的影响。以上研究均发现相变诱导塑性效应对焊接应力及残余应力产生重要影响，有助于识别堆焊层薄弱区域，为预防堆焊裂纹类缺陷提供理论依据。

目前对埋弧堆焊中传热、应力、相变的数值模拟研究，绝大多数是对温度与塑性应力的耦合分析或奥氏体-马氏体相变过程中马氏体体积膨胀对残余应力的影响进行研究。相变诱导塑性效应对堆焊应力演变及残余应力的影响、焊接组织相组成等方面的研究未见报道。因此，本文基于COMSOL 多场耦合平台，建立了埋弧堆焊过程中热-组织相变-塑性应力多场耦合的三维数值模型，对堆焊过程传热、相转变成分和相变塑性应力及残余应力进行数值计算，准确揭示了焊接过程中传热、相变塑性应力、马氏体相成分演变的规律，得出母材和堆焊层残余应力的分布特点，预测堆焊层下裂纹的发展趋势。

1 试验条件与材料

试验轧辊基材选取Q235 钢，成分见表1。堆焊过渡层选取YD263 焊丝，直径为φ4.0 mm，成分见表2，并选取260 焊剂。过渡层上再堆焊工作层，选取焊丝L458，直径为φ4.0 mm，成分见表3，并选取260 焊剂。采用自动埋弧堆焊机，焊接电流为345 A，堆焊电压为32 V，堆焊速度为0.22 m/min，堆焊热效率取80%，选取尺寸为24 mm×27 mm×7 mm 的堆焊试件，如图1 所示。

表1 Q235 元素组成Tab.1 Element composition of Q235 wt%

表2 YD263 的元素组成Tab.2 Element composition of YD263 wt%

表3 L458 的元素组成Tab.3 Element composition of L458 wt%

图1 堆焊试件Fig.1 Hardfacing test pie

2 轧辊埋弧堆焊过程建模的理论基础

2.1 埋弧堆焊过程微分方程

建模基于如下假设：（1）材料为各向同性均匀材料；（2）材料服从Mises 屈服准则；（3）允许目标阶段的塑性恢复，弥补前没有出现塑性应变；（4）通过施加一个初始应变表征基相组成的热膨胀和奥氏体引起的应变。埋弧堆焊过程控制方程为：

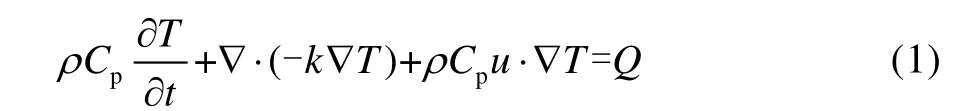
式中：ρ 为密度（kg/m3）；k 为热导率（W/(m·K)）；u 为速度（m/s）；Q 表示体积热通量。

计算采取双椭球热源，双椭球热源模型为：

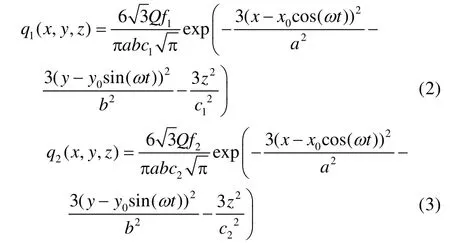
式中：x、y、z 分别代表热源中心坐标；q1、q2分别代表前、后半轴热流分布；a、b 分别是椭球模型的x、y 半轴长度；c1、c2分别是前后椭球体z 向的半轴长度；f1、f2是热源集中系数，且f1+f2=2；ω 为角速度；Q 表示体积热通量，Q=ηUI，其中η 是有效热功率，U 为堆焊电压，I 为堆焊电流。

埋弧堆焊过程中熔渣覆盖整个焊缝，减少了熔池表面的辐射和蒸发，堆焊层的对流热损失较少，而轧辊基体热损失较大，其对流传热更快。传热效率极大影响了堆焊塑性应力分布和马氏体相变分数。因此，对基体和堆焊层要使用不同的热对流系数来表征，为：

式中：q0为向内热通量；h 为对流换热系（W/(m2·K)）；T0为工件表面温度；Ta为环境温度（K）。

考虑焊接过程辐射换热，为：

式中：ε 为物体表面辐射率；σ 为玻尔兹曼常数。

2.2 埋弧堆焊过程多场耦合作用机理分析

堆焊原理如图2a 所示，为有效揭示焊接过程多场耦合作用机理，沿垂直轧辊轴线方向切取一定厚度的轧辊圆柱体为研究对象，圆柱外环为堆焊层，内侧为轧辊基体，热源沿着轧辊与堆焊层之间的缝隙移动，在轧辊与堆焊层之间形成局部微小熔池，实现冶金结合。因焊接凝固过程中温度变化梯度较大，导致高温塑性变形，焊缝金属凝固收缩产生焊接应力[14]，随后冷却过程中发生马氏体相变。焊接中多物理场间的相互耦合作用机理如图2b 所示。图3 是轧辊埋弧堆焊层实物图。

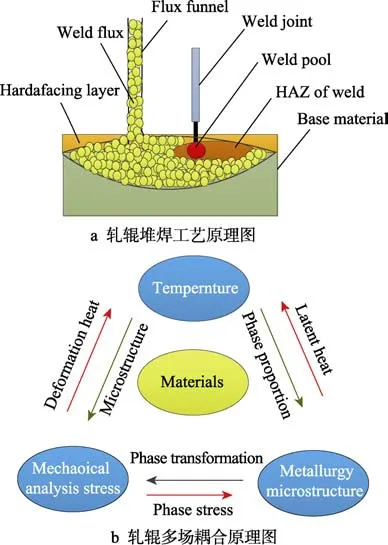
图2 轧辊埋弧堆焊过程及原理示意图Fig.2 Process and principle diagram of roll submerged arc welding

图3 轧辊堆焊焊道形貌Fig.3 Roll hardfacing weld bead morphology

3 轧辊堆焊过程多场耦合数值模拟

3.1 轧辊堆焊过程数值模型的建立

轧辊直径为50 mm，堆焊层厚度为5 mm。基于COMSOL5.5 建立埋弧堆焊模型。采用自由四面体划分网格，包含108 343 个域单元和14 413 个边界单元，如图4 所示。计算选取固体传热和固体力学，采用金属加工模块计算埋弧焊过程的温度场、应力场与相变过程，计算参数见表4。

为有效考虑焊接中材料参数的温变影响，利用CALPHAD 方法计算温变参数，将数据导入计算程序，得出基体和堆焊层的热物性参数温变曲线，如图5 所示。

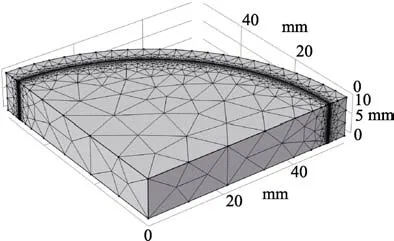
图4 轧辊埋弧堆焊有限元模型Fig.4 Finite element model of submerged arc welding

表4 埋弧堆焊工艺参数Tab.4 Process parameters of submerged arc welding

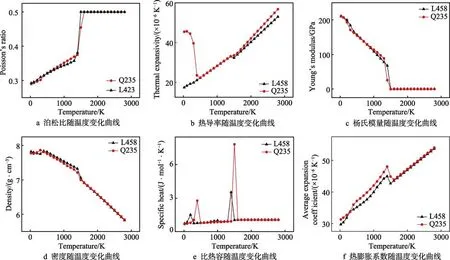
图5 轧辊基体和堆焊层的物性参数随温度的变化曲线Fig.5 Variation curve of physical parameters of roller substrate and hardfacing layer with temperature

3.2 计算结果分析

利用 DELL T7290/40 核工作站对轧辊堆焊模型进行求解，得出堆焊过程多场耦合计算结果。

3.2.1 温度场计算结果

提取轧辊埋弧堆焊过程0～1200 s 的温度分布，分别如图6a—j 所示。计算表明：在不同时刻，轧辊基体与堆焊层间形成了“椭球状”焊接熔池，椭球长半轴沿堆焊轨迹切线方向，短半轴沿与其垂直的法线方向。温度最高点出现在“椭球”中心偏后位置，该位置与焊接扫描方向相反，随着焊接的进行，焊接热影响区温度不断升高，直到形成准稳态温度场。随着堆焊热源的移动，熔池内温度场变化明显，靠近熔池芯部温度较高，由熔池芯部到熔池边缘温度呈现梯度递减分布。“椭球状”温度场逆着焊接方向形成“彗星尾”分布带。t=10 s 后，热源离开焊件，由于焊渣的保温效果，当t=20 s 时，堆焊层温度明显高于基体一侧，这对堆焊中应力分布状态与冷却过程中马氏体相变产生重要影响。当t=1200 s 时，试件已冷却至室温。图6k—l 为双椭球热源切面图。

图7 为轧辊埋弧堆焊温度采集轨迹。图8 为不同时刻沿图7 采集线绘制的温度变化曲线。1 号温度采集线位于基体上表面且与焊接扫描方向垂直，2 号温度采集线垂直于焊接方向且竖直，3 号温度采集线沿焊接轨迹的弧线方向。计算表明：沿1 号轨迹方向，温度呈现先上升后下降的变化趋势，与熔池芯部等距位置的外侧堆焊层温度明显高于内侧基体温度。堆焊进行到1 s 时，温度达到1128 K。随着焊接的进行，各时刻峰值呈现递减趋势，直至峰值消失。这是因为焊接热源扫过时，温度明显出现峰值，热源扫过后，温度逐渐回落所致。沿2 号轨迹线，不同时刻温度均呈现升高趋势，熔池中心温度出现峰值，1 s 时温度为1128 K。随着焊接的进行，各时刻峰值温度呈现递减趋势，熔池边缘温度稍有升高，但增加梯度逐渐减小，靠近熔池芯部的温度明显高于边缘的温度。3号轨迹上不同时刻温度出现峰值分布，峰值出现处的温度先逐渐增大后陡然递减，这种现象很好地揭示了双椭球焊接热源在焊接过程中不同位置的焊接影响规律，2 s 时温度达到2430 K。随着焊接的进行，峰值沿焊接方向规律性前移，清晰地展示了焊接热源向前推移的过程。图6b—e 分别为1、2、3、4 s 时刻埋弧堆焊过程中沿3 条轨迹线上4 个不同位置点的温度变化图。其中图6b—e 和图7 中为选取沿3 条轨迹线上相互距离为2.5 mm 的4 个点。由图6b 可知，t=1 s时刻沿 1、2、3 号轨迹线温度分布范围依次为396～1090、420～1090、293～2370 K。图6b—e 准确反映了不同时刻沿3 条轨迹线上4 个位置点瞬时温度的变化，且与图8a—c 中沿1、2、3 号轨迹线中相同位置各点的温度变化相一致。

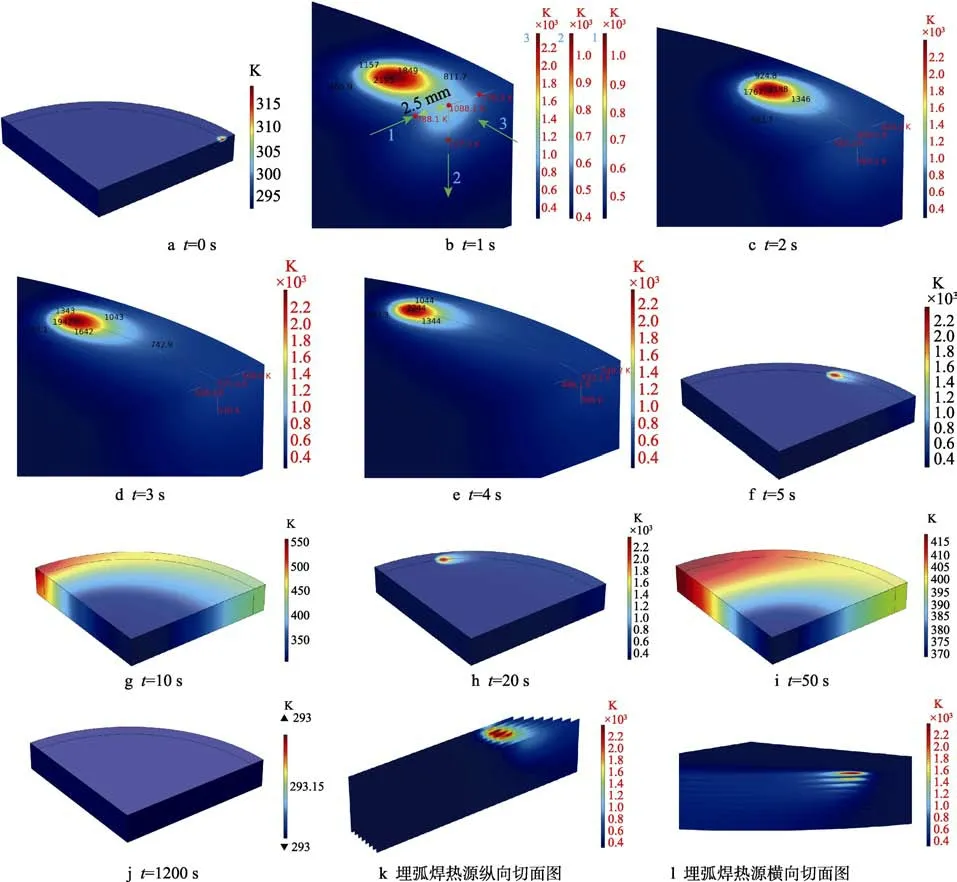
图6 轧辊埋弧堆焊过程温度场分布Fig.6 Temperature field distribution of roll submerged arc welding

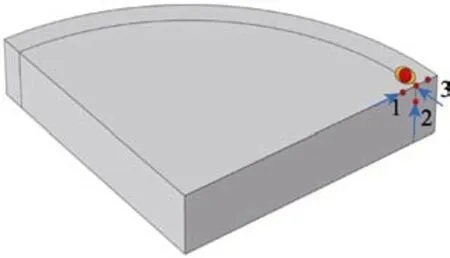
图7 轧辊埋弧堆焊温度采集轨迹Fig.7 Temperature acquisition track of roll submerged arc welding

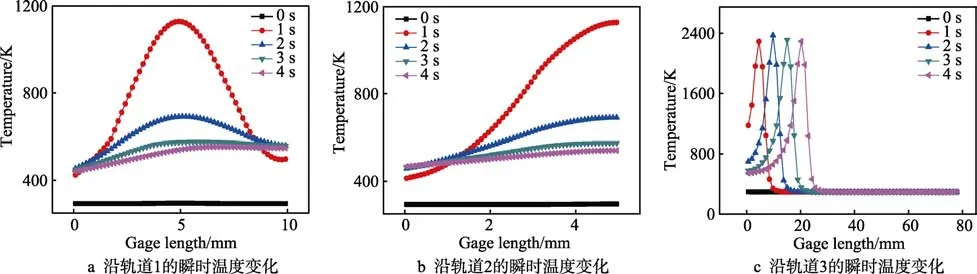
图8 埋弧堆焊不同位置的温度变化曲线Fig.8 Temperature variation curve at different positions of submerged arc welding

3.2.2 相变塑性应力场计算结果

在堆焊过程中存在热-力耦合作用，母材与堆焊层均发生相变塑性变形[15]。在受到机械应力作用时发生相变，相变应变会产生应力和变形，产生转换诱导塑性（TRIP）。

应力依赖于应变，应变依赖于位移。基于小应变有：

式中：ε 是应变； ∇u 位移矢量梯度。

应变率取决于速度，有：

式中：d 是应变率； ∇v 是速度梯度。

总应变方程为：

式中：ε 是总应变；εel弹性应变；εpl塑性应变；εth是热-冶金应变；εtr为热膨胀应变；εtp是相变塑性应变。弹性变形遵循Hooke 定律，其大小与弹性模量有关，见式(9)。质量密度可写成相分数密度的加权之和见式(10)。

式中：σ 是应力；E 是四阶弹性张量；ρ 是密度；ρi是各相密度；φi是各相的相分数。每个分数的质量密度都是温度的函数，变化的速度写成：

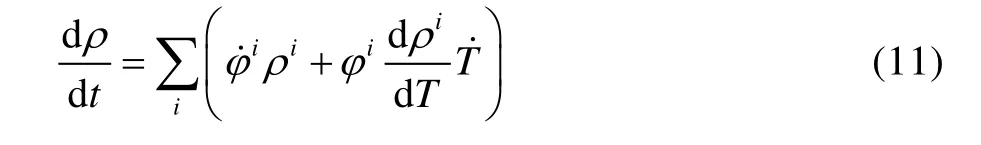
式中：T 是温度；t 是时间；T˙是温度对时间的导数。

对于各向同性材料，密度变化与应变关系为：

相变和热膨胀引起的应变速率为：

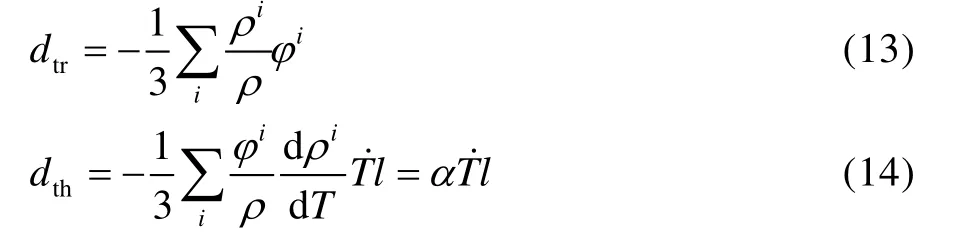
式中：α 是与热膨胀相分数相关的系数；l 是二阶单位张量。

相变诱导塑性应变速率见式(15)[16]，函数Fi、φi决定了相变过程中的塑性变化。常数Ki取决于钢的化学成分和相变类型。

计算得出轧辊埋弧堆焊过程中瞬时相变塑性应力。图9a—f 分别为0～1200 s 内堆焊相变塑性应力分布云图。结果表明，熔池芯部应力明显低于周围热影响区应力。随着焊接的进行，沿着焊接轨迹形成塑性应力带，应力带靠近基体一侧分布较宽，应力值较大且更加集中，在焊接垂直方向应力由焊缝向外侧呈现梯度递减，在熔池前端产生明显应力。t=10 s 后，焊件开始冷却，在冷却过程中，一方面基体材料会发生变形，热应变由温度变化引起，而机械应力则引起相变诱导塑性；另一方面，当温度达到马氏体相变温度时，将发生由奥氏体向马氏体的转变，因体积膨胀，母材受拉应力，同时受到堆焊层压应力，导致相变塑性应力短暂下降。当冷却到t=1200 s 时，整个试样温度分布趋于一致，达到室温，此时的应力即为残余应力，达376 MPa。

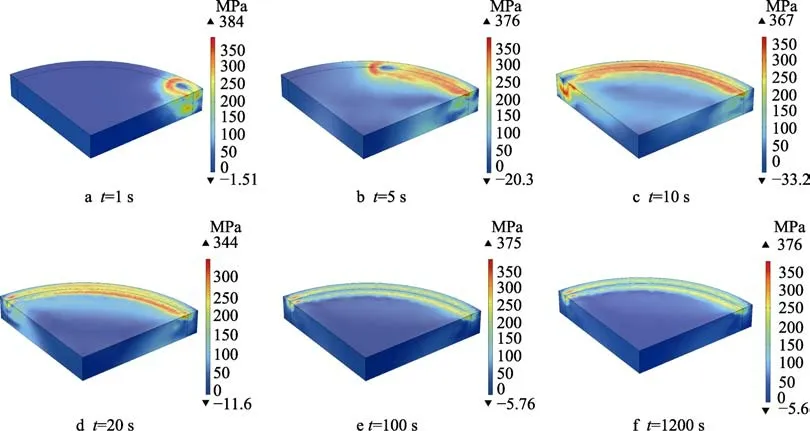
图9 埋弧堆焊相变塑性应力场演变规律Fig.9 Evolution law of transformation plastic stress field of submerged arc welding

为更好地揭示堆焊中相变塑性应力场分布，沿图7 中1、2、3 号路径提取应力，分别绘制曲线，如图10 所示。计算表明：图10a 为沿1 号采集线的应力曲线，沿1 号采集线应力逐渐上升，接近焊缝处的应力趋于平稳，在7.5 mm 处应力开始逐渐下降，10 mm处为堆焊层表面，由拉应力变为压应力，相变塑性应力最大值为–19.4 MPa；图10b 为沿2 号采集线的应力曲线，应力不断上升，接近热影响区位置，应力陡升至325 MPa，随着热源的移动，应力逐渐趋于稳定；图10c 为沿3 号采集线的应力曲线，应力最大值达到384 MPa，呈现先下降后升高，然后再降低的单峰分布。在不同时刻，峰值变化平缓，峰值随着焊接的进行不断规律性前移，揭示了焊接热源移动对应力分布的影响。

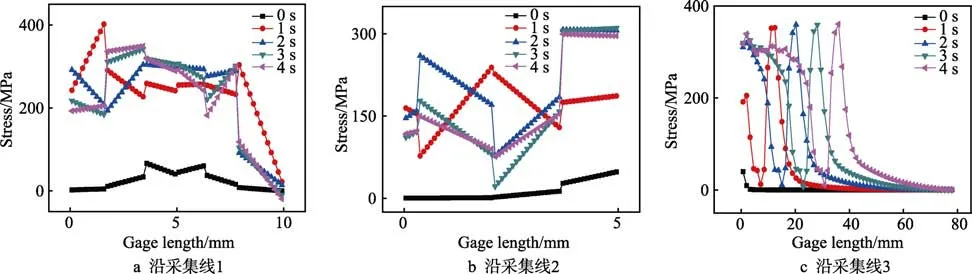
图10 沿不同采集线的相变塑性应力曲线Fig.10 Transformation plastic stress curves along different acquisition lines

3.2.3 埋弧堆焊过程相转变

因奥氏体到铁素体或珠光体的相变具有扩散性，采用Leblond-Devaux 相变模型进行建模见式（16）。模型热导率、密度、比热容与温度有关，但在冶金相变时，也取决于相组成[17]。

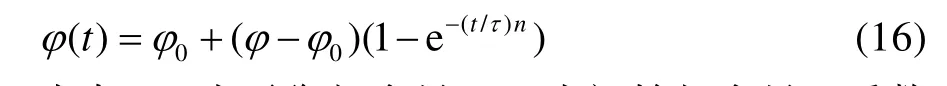
式中：φ 为平衡相含量；φ0为初始相含量。系数n 和τ 与成核频率和生长速率有关。

马氏体相变用Koistinen-Marburger 模型描述[18]。该模型认为，在奥氏体转化为马氏体的过程中，转化的数量取决于可用奥氏体的比例和低于马氏体起始温度Ms的过冷。马氏体形成的速率与温度冷却速率和奥氏体的瞬时分数成正比。微分形式下的模型为：

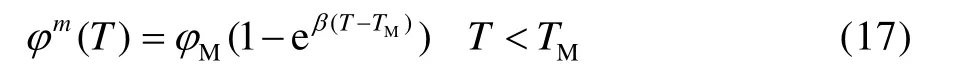
式中：φM是残存奥氏体含量；TM是马氏体相变起始温度；T 是当前温度。

3.2.4 马氏体相变计算结果

基于CALPHAD 法计算得出母材和堆焊层的马氏体转变的温度变化参数，导入COMSOL 计算得出埋弧堆焊过程相成分的演变规律，如图11 所示。其中，红色为马氏体、蓝色为奥氏体。计算表明，随着堆焊热源的移动，在靠近热源的区域温度先达到奥氏体转变温度，铁素体发生向奥氏体的转变。随着热源的离开，温度开始快速下降，奥氏体相又逐渐转变为马氏体相。轧辊基体冷却速率由传热系数、表面与外界温差决定。靠近基体侧的温差更大，冷却速率更高，奥氏体等扩散控制的相变将受到限制，有利于位移马氏体相变。冷却至室温时，堆焊层的马氏体相含量为94%。

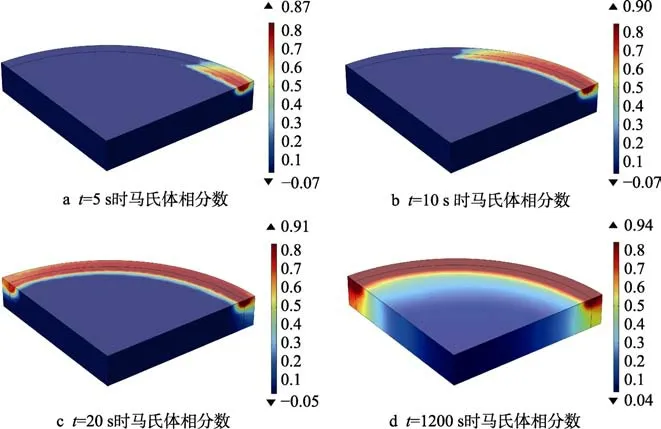
图11 埋弧堆焊相变演变规律Fig.11 Evolution law of phase transformation in submerged arc welding

4 埋弧堆焊过程金相实验

对埋弧堆焊试样进行抛光，用王水腐蚀处理，利用Zeiss-ΣIGMA HD 场发射扫描电子显微镜观察堆焊组织，如图12 所示。图12a 是基体与堆焊层组织。可见，堆焊区域中基体、堆焊层及过渡区存在明显分界。上方区域为堆焊层，下方区域为基体，中间为热影响过渡区域。图12a 中堆焊层金相组织放大为图12b，j和g 处绝大部分区域均为马氏体，h 和i 处为黑色碳化物[19-20]，与数值计算结果吻合，验证了模型的有效性。

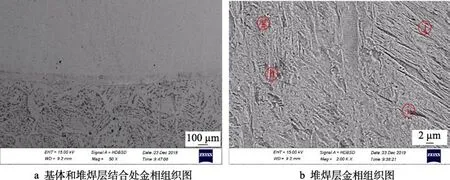
图12 埋弧堆焊金相图Fig.12 Metallographic diagram of submerged arc welding

5 结论

1）建立轧辊埋弧堆焊过程三维多场耦合数值模型，对模型进行求解，得出堆焊中温度场、相变塑性应力场、相变分数的变化规律，为确定埋弧堆焊过程优化工艺参数提供理论依据。

2）计算表明，堆焊中形成了“椭球状”焊接熔池，温度场逆着焊接方向形成“彗星尾”分布带；熔池应力明显低于周围热影响区，由熔池芯部向外围应力呈现梯度递减。随着焊接的进行，沿着焊接轨迹形成塑性应力带，应力带在靠近基体一侧较宽，应力值较大且更加集中。随着堆焊热源的移动，在靠近热源的区域温度先达到奥氏体转变温度，铁素体发生向奥氏体的转变，随着温度继续下降，开始发生马氏体相变，冷却至室温时马氏体含量为94%。

3）利用Zeiss-ΣIGMA HD 场发射扫描电子显微镜对埋弧堆焊试件进行金相实验，验证了模型计算的有效性。