基于代数图论的修正贝叶斯群目标航迹起始算法
2021-04-06张天然
姜 琦 王 锐 周 超 张天然 胡 程
(北京理工大学信息与电子学院雷达技术研究所 北京 100081)
(北京理工大学卫星导航电子信息技术教育部重点实验室 北京 100081)
1 引言
针对空中集群生物的探测与跟踪对人造设施防撞、农业灾害预警、生物学研究等均具有重要意义,已成为雷达学界的热门研究领域[1,2]。探测空中集群生物的雷达可分为监测大范围生物群体迁徙的雷达(如监测鸟类、昆虫迁徙的天气雷达)[3]和获取小范围生物目标的航迹、特征参数等信息的雷达(如机场防鸟撞雷达)[4],本文以第2种雷达为研究背景。为了能够持续跟踪并提取集群生物目标的特征信息,首先需要起始各个生物集群目标的航迹,具体包括分群检测与航迹确认两个步骤。
分群检测的目的在于将监测空间内得到的量测集合按照一定的规则划分为若干子集[5]。以态势估计等应用为背景的分群算法(如D-S证据理论[6]、模板匹配法[7]、贝叶斯网络分群法[8],聚类算法[9,10]等)需要事先给定分群数量或模板,适合编队目标的分群,不适用于生物集群目标。近期,基于相似度矩阵的分群算法得到较多关注[11–13],此类方法不需要目标个数等先验信息,分群结果不受点迹顺序影响,能正确反映跟踪期间群目标的动态变化。但现有相似度矩阵法需要同一个群内所有目标两两相似,在集群生物场景中易导致边缘个体被排除在外,或属于某个子群的目标被误分至另一个子群内等错误结果。
分群检测后需要计算各个子群的等效量测,计算方法包括K-方法、集群引晶法[14]、几何中心法[5]、重心法[15,16]、距离-幅度加权法[17]等。得到等效量测后转入航迹确认步骤,总体上可分为顺序处理和批处理两大类[18]。现有群目标航迹确认方法通常沿用传统单目标航迹确认策略,利用等效量测信息计算航迹为真的后验概率,如修正的逻辑法[17]和基于运动补偿的航迹起始方法[19]等。然而航迹起始阶段的非理想量测因素会导致等效量测点状态不稳定,降低了传统航迹起始算法的效率。
基于以上问题,本文提出基于代数图论的修正贝叶斯群目标航迹起始算法,引入代数图论定量描述监测空间内目标间的相似关系,根据连通图性质完成分群计算;在经典贝叶斯框架的基础上对似然比的定义予以修正,用泊松分布描述群内量测数目的特性,避免了因等效量测残差过大导致航迹确认出现错误。实测数据处理结果证明,本文提出的航迹起始算法能够准确划分监测空间内的群目标,拥有比传统贝叶斯航迹确认算法更优的性能。
2 基于代数图论的修正贝叶斯群目标航迹起始算法

2.1 基于代数图论的分群检测算法
本文引入代数图论思想,用 nk个顶点(vertex)表示量测集合内的nk个 点迹,顶点集记为{ v1,v2,···,vnk};如果两个目标点迹根据一定准则判为相似,则用1条边(edge)将两个相似点迹对应的顶点vi和vj连接起来,称 vi和vj相 似;将得到的图记为 Γ;定义图Γ的相似度矩阵A (Γ)内的元素为
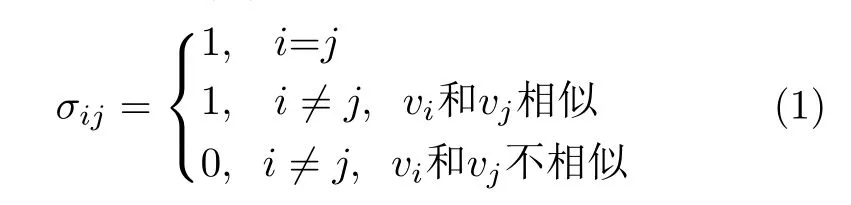
由此得到相似度矩阵。各个点迹默认同自身相似,因此相似度矩阵为对角线元素全为1的0-1二值对称矩阵。若多个点迹被划分至同一个群目标内,该群对应的图中任意两个顶点都能通过一定的步长(walk)相连,这种图称为连通图(connected graph)。对相似度矩阵进行初等行列变换,将1元素汇聚到对角线上的多个分块方阵内,检查各个非零分块方阵内的元素对应哪些点迹,即可得知各个群目标包含哪些目标。
相似度矩阵法需要检测对角线上的非零分块方阵,要求分块方阵内的元素全部为1,即同一个群内的所有目标两两相似。如果分块方阵内元素不全为1,分群结果就会出错。该方法对密集机群等编队目标可取得较好的效果,此类目标内部个体相互间的距离通常较为接近。但由于生物集群目标(如迁徙鸟群)常采用“人字形”、“一字形”等编队方式,队形边缘个体之间的距离通常远大于相邻个体间的距离。此时为了保证群内所有个体两两相似,相似门限必须大于相距最远的两个体间的距离,导致相似门限过大,很容易将不属于该群的目标误分至该群内。以图1为例,监测空间内有2个鸟群,分别以“人字形”和“一字形”编队飞行,需分别跟踪;在分群检测时,为了保证上方“人字形”编队边缘的 a1个 体与a2个体相似,门限必须大于状态空间的距离 l1; 由于l1>l2,这会导致下方“一字形”编队的个体b1同 样与a1相似,造成分群结果出错。
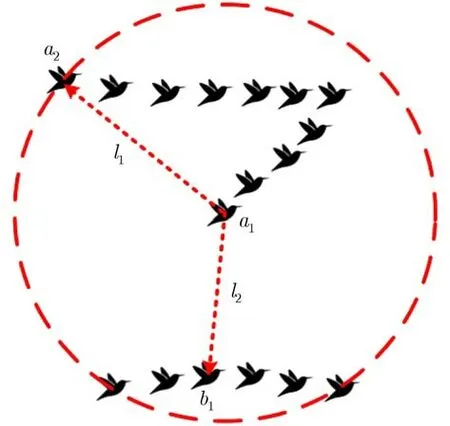
图1 传统相似度矩阵法在应用中的局限性
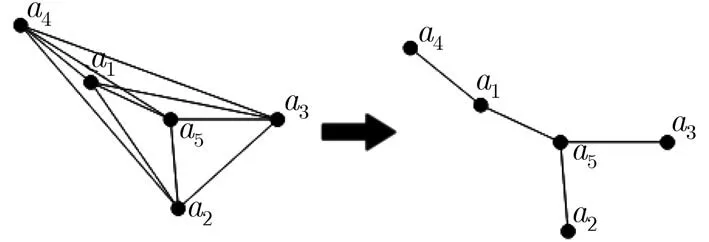
图2 简化后的相似度关系
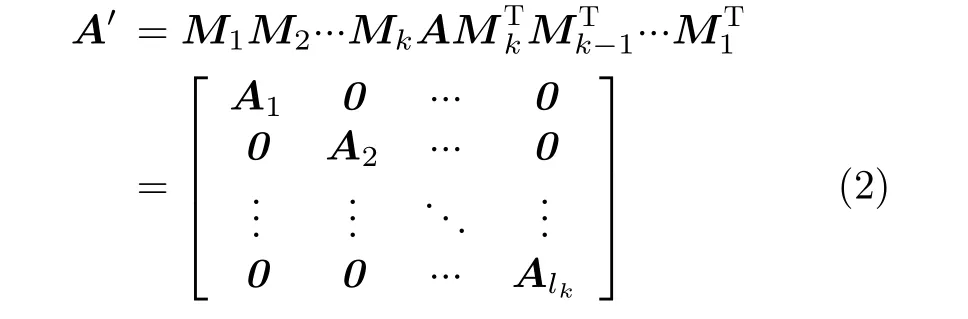
根据代数图论的结论,拥有 m个顶点的图 Γ是阵M1,M2,···,Mk,将同一个子群内的目标全部排列至对角线上的分块矩阵内,即连通图的充要条件是其相似度矩阵 A 的m −1次幂Am−1内部元素均为非零元素[22];容易证明,当拥有 m 个顶点的图是连通图时,矩阵An−1(n ≥m)内部同样均为非零元素。根据上述性质,如果监测空间内的 nk个 点迹同属一个群目标,那么矩阵Ank−1内部均为非零元素。实际情况中,监测空间内常含有不止1个群目标,假设nk个 点迹属于lk个子群,根据相似度矩阵的定义,如果能找到初等行列交换矩

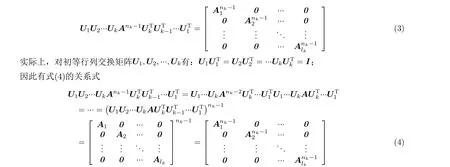


(3)完成步骤(1)和(2)后,若从第2行第3列元素开始,直至第2行第i列的矩阵元素值连续不为0,则判定此连续若干列所对应的量测同属一个群目标;再从第i+1行第i+2列开始,按照同样的步骤进行行列交换和判定操作,以此类推直至完成第nk+1行 第nk+1列操作,所有非0元素构成多个分块矩阵B1,B2,···,Blk,即
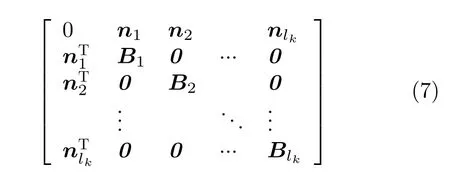
(4) 提取并记录向量n1,n2,···,nlk内部的数字,得到各个群目标内点迹的编号,计算 lk个子群的等效 量测。
2.2 修正的贝叶斯航迹确认算法
分群检测完成后,需要判断航迹是否为真,本文将此过程称为群目标航迹的预起始阶段。预起始阶段的结果有两种:确认航迹为真并转入跟踪滤波,或者确认为假并丢弃。基于贝叶斯框架的航迹确认算法是实际中常采用的方法,其核心是根据当次扫描得到的量测集合计算航迹为真的后验概率,其递推形式为[23,24]
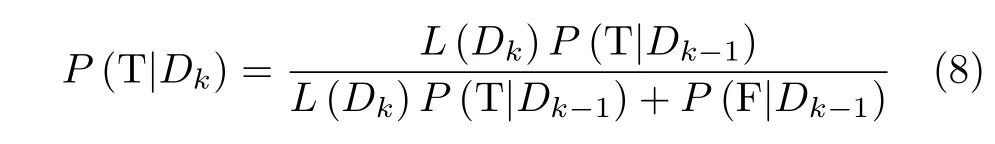
其中, T 表示量测属于真实航迹的事件, F表示量测来自虚假回波的事件,L (Dk)为似然比
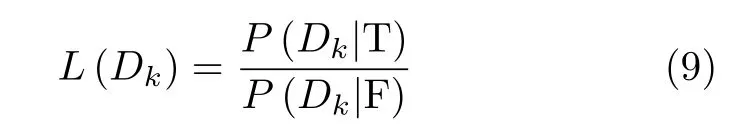
其中,P (Dk|T)表示航迹为真条件下得到量测集合Dk的概率,P (Dk|F)表示航迹为假条件下得到量测集合 Dk的概率,P (T|Dk)表示第k时刻航迹为真的后验概率。
意美(即建筑美)。这三个翻译版本来看,题目是不同的,首先,这三个版本都采用形容词修饰名词的结构,“未选择的路”“未选之路”“未踏之径”。区别在于顾版译文采用白话文的形式。诗的题目为“Theroad not taken”是过去分词做后置定语,可见题目翻译与原诗歌在句式结构上较为贴合。
经典单目标、多目标跟踪场景中,P (Dk|T)的定义为航迹为真条件下在已知的具体位置得到量测点的条件概率。由于群目标在航迹起始阶段受到多种非理想因素(如分辨率受限、部分目标未进入监测空间、视线遮挡等)的干扰,导致等效量测的计算值和预测值存在较大残差,降低了似然比的值,从而导致航迹确认性能的下降。
本文所提修正的贝叶斯航迹确认算法,对P(Dk|T)的定义进行修正,以1个子群内有nk个量测点为例
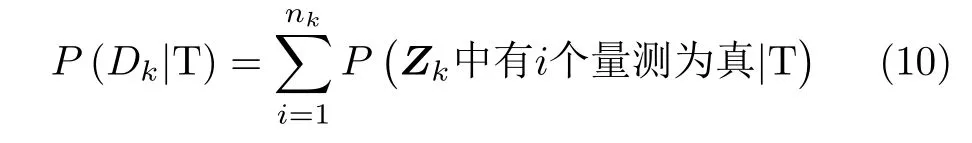
式(10)的计算涉及复杂的条件概率求解。空中集群生物通常飞行高度较低,雷达回波内存在较多杂波干扰分量,在雷达进行跟踪前应首先进行杂波点迹剔除。本文针对的是杂波剔除处理后的群目标航迹起始问题,此时可认为在监测空间内残留虚假点迹是小概率事件,同时出现多个虚假点迹的概率更小,因此可以对P (Dk|T)做以下简化处理
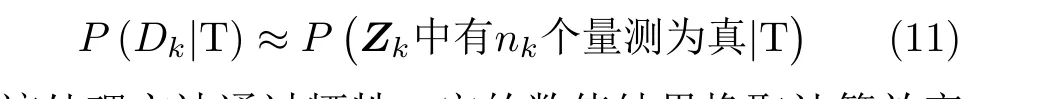
该处理方法通过牺牲一定的数值结果换取计算效率的提升。本文利用泊松分布描述当群目标真实存在时量测集合包含nk个点迹的概率
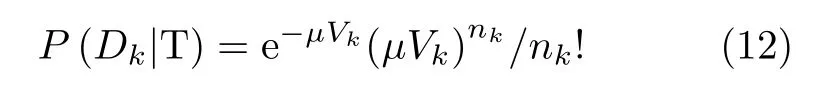
其中, Vk表 示群体积,µ 表示与群目标密度相关的系数。本文认为虚假量测在整个空域中满足独立、均匀分布,则P (Dk|F)的表达式可写为
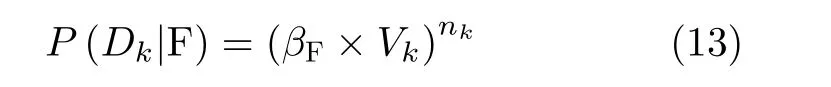
其中,βF表 示监测空间中的虚假量测密度系数。完整的似然比表达式为
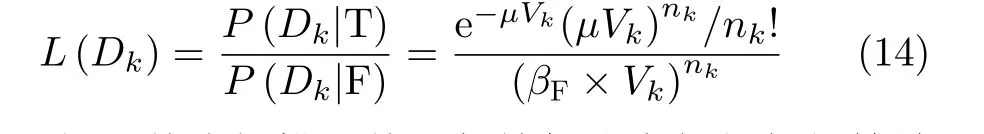
如果某次扫描后某预起始航迹未能与任何等效量测进行关联,则利用上一时刻的预测状态作为该预起始航迹当前状态的外推,似然比变为量测缺失情况下的表达式
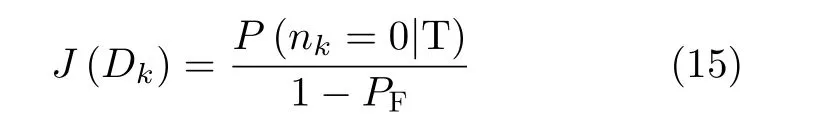
其中, P (nk=0|T)是雷达在群目标存在的条件下未能检测到任何真实量测的概率,令式(12)中的nk=0 即可求得;PF是雷达在监测空间内至少得到1个虚假点迹的概率
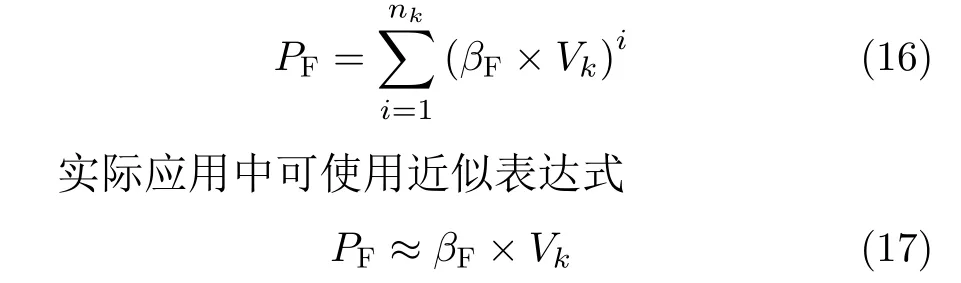
修正的贝叶斯航迹确认算法完整步骤如下:
(1) 雷达在第k时刻对回波进行恒虚警检测和分群检测后得到某个新群目标的量测集合 Dk,计算 Dk的等效量测z ˜k;此时等效量测z ˜k无法与任何现有航迹或预起始航迹进行关联,将z ˜k记录为预起始航迹点,该预起始航迹为真的先验概率记为P0(T);根据目标的自身性质设定下一时刻的关联门范围;
(2) 若k+1时刻有量测集合Dk+1的等效量测点z˜k+1落入关联门,则转入步骤(3);若没有等效量测点落入关联门,转入步骤(4);
(3) 根据当前时刻(记为i, 泛指i ≥k+1的任意时刻)量测集合 Di的目标个数信息ni和群体积信息Vi,利用式(14)计算似然比结果;根据式(8)计算航迹为真的后验概率 P (T|Di) ;如果P (T|Di)>γT,则判定预起始航迹为真并转入航迹状态初始化处理;如果P (T|Di)<γF,则判定预起始航迹为假并丢弃;如果 γF
(4) 利用上一时刻的预测状态作为预起始航迹在当前时刻状态的外推;利用式(15)计算似然比结果;根据式(8)计算当前时刻(记为i, 泛指i ≥k+1的任意时刻)航迹为真的后验概率 P (T|Di);如果P (T|Di)>γT,则判定预起始航迹为真并转入跟踪滤波处理;如果P (T|Di)<γF,则判定预起始航迹为假并丢弃;如果 γF
(5) 将外推状态与当前时刻计算得到的等效量测进行关联,如果有新的等效量测关联成功,则重复步骤(3)的处理流程,直至航迹为真的后验概率P (T|Di)在 第i时 刻大于门限γT(判断航迹为真)或小于门限 γT(判定航迹为假);如果未能和任何新等效量测关联成功,则重复步骤(4)的处理流程,直至航迹为真的后验概率 P (T|Di) 在第i时刻大于门限γT(判断航迹为真)或小于门限γT(判定航迹为假)。
3 实验数据处理与分析
本论文依托的项目课题组于2019年10月在东营实验基地采集了鸟群的雷达回波数据,本节利用鸟群实测数据的距离和数量信息验证分群检测与航迹确认算法的有效性,给出了实测数据处理结果和与经典方法的对比分析。
3.1 实验场地和设备介绍
课题组于2019-10-10—2019-10-11, 2019-10-12—2019-10-13分别在东营市天鹅湖公园和黄河南大堤开展了雷达探鸟实验。实验地点附近湿地、水域面积较大,鸟类的种类和数量丰富,又处于候鸟迁徙通道,适合开展鸟类观测实验。实验地点和现场图如图3所示。

3.2 实测鸟群数据处理结果分析
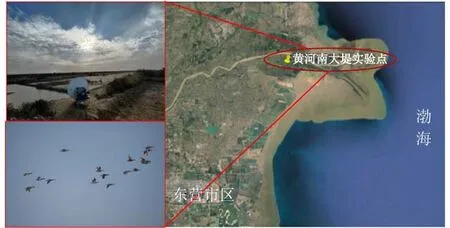
图3 黄河南大堤观测实验位置和实验现场图
为全面对比分析本文提出的航迹起始算法针对不同场景的处理性能,本小节选取不同场景下的实测数据对比了本文提出的航迹起始算法和经典航迹起始算法的性能,具体包括:(1)单目标航迹起始性能对比;(2)单群目标航迹起始性能对比;(3)多群目标航迹起始性能对比。所有数据在分群检测和航迹起始处理前已经过杂波抑制和虚假点迹剔除,可认为虚假点迹满足稀疏和均匀分布条件。
3.2.1 单群目标航迹起始性能对比
2019年10月13日下午14:17,实验团队在黄河南大堤采集到了约700 m高度处的6只雁类个体组成的鸟群回波数据,鸟群在雷达波束内的驻留时间约2.5 s,如图4所示。图5给出了本文提出的基于代数图论的修正贝叶斯群目标航迹起始算法和传统贝叶斯航迹起始算法应用于群目标回波的效果对比,其中红色五星代表初始帧的群目标等效量测,洋红方块代表预起始阶段等效量测,绿色圆圈代表航迹确认起始并转入跟踪滤波的等效量测,红色叉号代表航迹被丢弃。本文提出的算法首先完成量测空间的子群划分,再利用修正的贝叶斯航迹确认算法计算航迹为真的后验概率,经过3帧数据后成功确认航迹存在,转入跟踪滤波流程;而传统贝叶斯航迹起始算法由于第3帧数据等效量测的预测值和真实值之间的残差过大,导致后验概率低于门限,被错判为虚假航迹。
3.2.2 多群目标航迹起始性能对比
2019年10月13日下午15:46,实验团队在黄河南大堤采集到了300~400 m高度范围内的多个鸟群回波数据,包括1个单目标和2个群目标,从中截取了一段同时存在1个单目标和2个群目标的数据进行处理。图6给出了本文所提分群检测算法对多个单/群目标的分群结果,以及航迹起始算法的结果对比。其中红色五星代表初始帧的目标等效量测,洋红方块代表预起始阶段等效量测,绿色圆圈代表航迹确认起始并转入跟踪滤波的等效量测。由图6(a)可知,本文提出的分群检测算法能够正确划分监测空间内的3个单/群目标;单目标经过4帧数据后确认航迹存在,2个群目标分别经过2帧和3帧数据后确认航迹存在;在正确分群的基础上,传统贝叶斯航迹起始算法的处理结果如图6(b)所示,单目标经过3帧数据后确认航迹存在;2个群目标经过3帧数据后确认航迹存在。由于该组数据等效量测变化较为平稳,传统算法未出现航迹误丢弃的现象,总体来看,该场景下本文算法对群目标的航迹起始效率优于传统算法。

图4 6只个体组成的鸟群现场照片和雷达回波
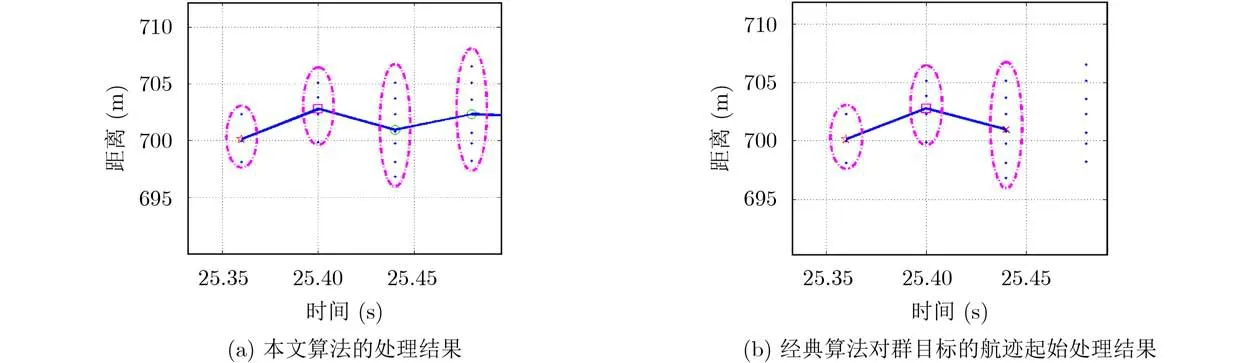
图5 单个群目标航迹起始结果对比
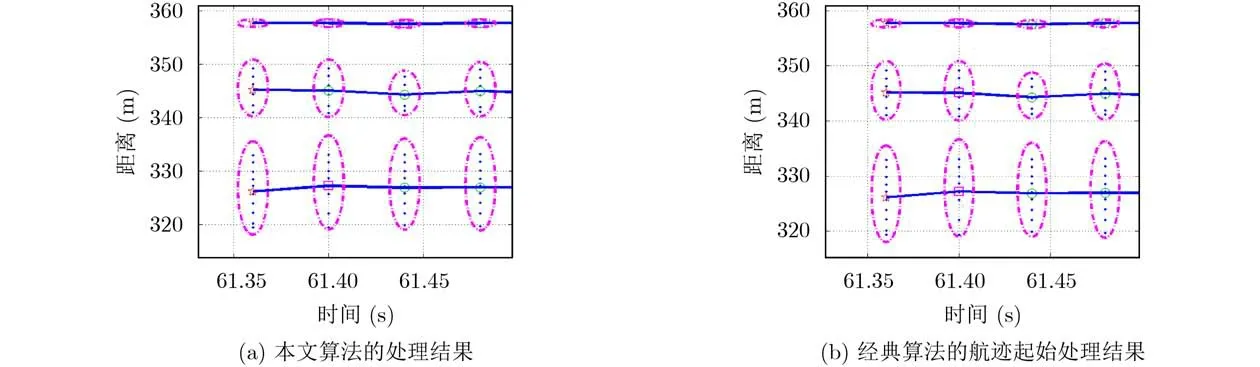
图6 多个单/群目标处理结果对比
4 结束语
本文针对空中集群生物目标跟踪问题,提出一种基于代数图论的修正贝叶斯群目标航迹起始算法。引入代数图论和连通图的性质后,本文所提基于代数图论的分群检测算法能准确划分量测集合内的各个子群目标,放宽了现有分群矩阵方法对群内目标的相似度限制,实现了群目标量测集合的准确划分;对经典贝叶斯航迹起始算法的似然比定义进行修正后,本文所提航迹确认算法提升了针对群目标(特别是密集群目标)的航迹确认效率,避免了经典贝叶斯航迹起始算法因等效量测残差过大导致航迹误丢弃。实测数据处理结果证明本文提出的算法针对群目标的航迹起始性能超过了经典贝叶斯算法,同时保留了针对单目标的优良航迹起始性能。
