广义Pareto分布海杂波背景下非相干检测器恒虚警性能分析
2021-04-06水鹏朗
张 坤 水鹏朗
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
1 引言
传统的非相干积累恒虚警(Constant False Alarm Rate, CFAR)检测方法是在保持虚警率恒定条件下将待检测单元的功率与估计的杂波功率的比值和检测门限进行比较判别以确定目标信号是否存在的方法[1–4]。高斯海杂波背景下的非相干恒虚警检测器对杂波功率是CFAR的。然而,随着雷达分辨率的提高和擦地角的减小,海杂波表现出了强非高斯特性。在对海雷达的整个探测场景中,海杂波的非高斯性可能会随着距离、方位以及时间的变化而变化。因此,有必要研究海杂波的非高斯特性以及非高斯海杂波背景下的非相干检测器的CFAR特性。复合高斯模型可以很好地描述海杂波的非高斯特性。复合高斯模型可以描述为一个慢变的非负纹理分量和一个快变的复高斯散斑分量的乘积[5–8]。当纹理分量服从Gamma分布时,海杂波幅度服从K分布,并且该模型已广泛应用于非高斯杂波建模和目标检测[8–11]。具有逆Gamma分布纹理分量的广义Pareto分布被用来描述具有重拖尾的非高斯海杂波[12–16]。研究表明,相比于K分布模型,广义Pareto分布更适合用于描述海杂波的强非高斯特性[16]。
非相干积累CFAR检测器以其计算简单、时间代价低的优势受到广泛应用。单元平均CFAR(Cell-Averaging CFAR, CA-CFAR)检测器通过参考单元雷达数据的算术平均估计杂波的功率水平。相比于CA-CFAR,有序统计量CFAR(Order-Statistic CFAR, OS-CFAR)检测器具有较好的对抗多目标和异常单元的能力。在高斯海杂波背景下,对于给定的虚警率,非相干检测器的检测门限是恒定的[1]。然而,这一情况对于非高斯海杂波下的非相干CFAR检测器是不适用的。在非高斯海杂波背景下,非相干CFAR检测器的门限与海杂波的非高斯性能有关。文献[17]研究了具有相关散斑分量的复合高斯海杂波下的非相干CFAR检测方法,但是在实时雷达系统中难以计算出CFAR检测门限。此外,由于海杂波的非平稳性能,复合高斯海杂波散斑分量的相关性也会随着距离、方位和时间的变化而变化。文献[18]在基于时频分析特征的目标检测方法中,使用了块白化方法在目标检测前对海杂波进行白化处理抑制海杂波,以提高检测性能。因此,为了确保全场景CFAR检测,不仅研究海杂波非高斯性对非相干检测器CFAR特性的影响,也要研究海杂波散斑分量的相关性对非相干检测器CFAR特性的影响。
本文研究了广义Pareto分布海杂波背景下CACFAR和OS-CFAR非相干检测器的CFAR特性。为了保证全场景CFAR检测,预先通过白化方法将具有相关性的海杂波去相关。与此同时,应用查表方法获得匹配杂波形状参数、积累脉冲数和参考单元数的检测门限,确保非相干检测器对此3个参数的CFAR性能。本文安排如下,第2节详细介绍广义Pareto分布海杂波背景下全场景CFAR的CACFAR和OS-CFAR非相干检测器;第3节通过实验验证两种检测方法的CFAR特性和检测性能;第4节总结全文。
2 广义Pareto分布海杂波背景下全场景CFAR的非相干检测器
雷达目标检测问题可以公式化为式(1)的2元假设检验问题

其中,散斑分量u 是0均值、协方差矩阵R=E{uuH}的N维复高斯随机向量,E{}表示取数学期望;纹理分量 τ是非负的随机变量,服从双参数的逆Gamma分布
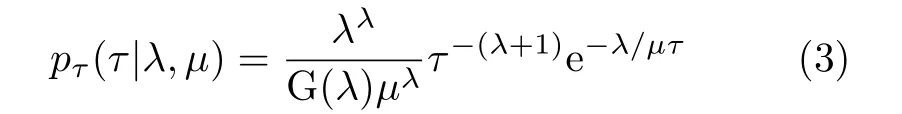
其中, µ是尺度参数,λ 是形状参数,G (·)表示伽马函数。在这种情况下,海杂波幅度服从广义Pareto分布

其中,r是海杂波的幅度,尺度参数 µ和形状参数λ共同决定杂波的功率水平,形状参数λ 决定杂波的非高斯性能。广义Pareto分布模型的尺度参数µ和形状参数λ 已知或者可以从雷达回波数据中预先估计[12–16]。
在本节中,分析广义Pareto分布海杂波背景下CA-CFAR和OS-CFAR两种非相干检测器的CFAR特性。CA-CFAR和OS-CFAR两种检测器的检测统计量分别为
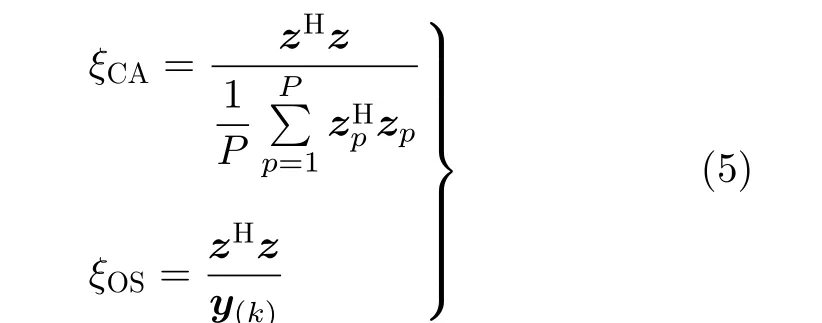



全场景CFAR检测的CA-CFAR和OS-CFAR检测器的原理框图如图1所示。首先对雷达回波进行白化处理,但是如果对每个分辨单元的回波进行白化处理,会大大增加处理时间,如此就失去了非相干检测器在计算时间上的优势。故而,利用海杂波的短时平稳特性,可以使用块白化方法对雷达回波进行去相关处理[10,18]。然后,在块白化后的雷达回波中使用CA-CFAR和OS-CFAR检测器检测目标。特别注意的是,检测门限是通过蒙特卡罗实验离线获得的,建立了不同参数条件下的检测门限表格。目标检测时,根据给定的海杂波形状参数 λ、积累脉冲数 N 、参考单元数 P和虚警率Pfa,通过查表获得检测门限。然而,由于网格化误差的存在,检测门限表格的精细程度会在一定程度上影响检测器的CFAR性质,所以基于查表的目标检测器可以保 证一种精度可以控制的近似CFAR。
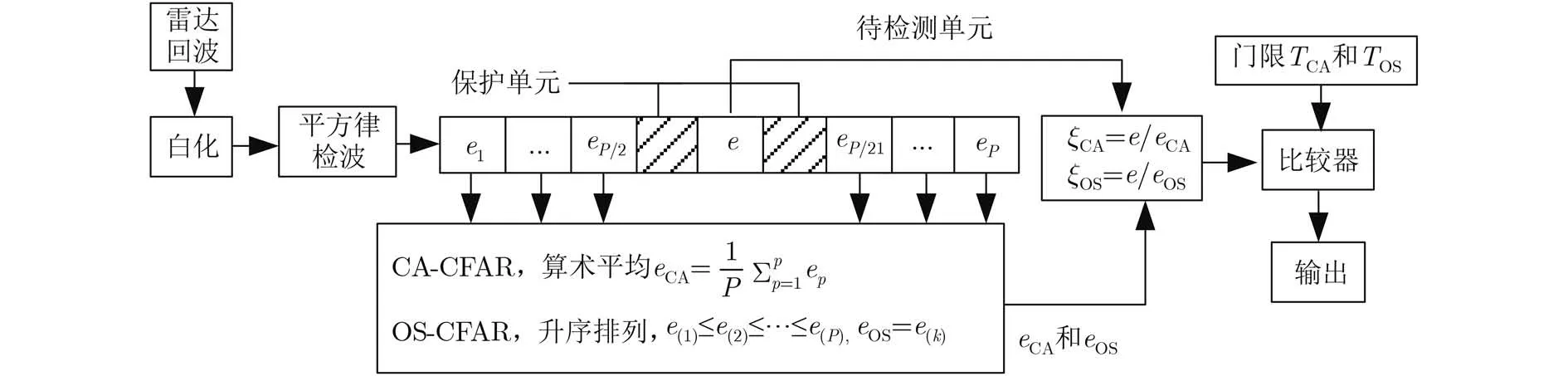
图1 全场景CFAR检测的CA-CFAR和OS-CFAR检测器的原理框图
3 实验结果与性能分析
3.1 CFAR特性分析
在本节中,通过仿真实验研究广义Pareto分布背景下CA-CFAR和OS-CFAR检测器的CFAR特性。广义Pareto分布海杂波通过式(15)仿真
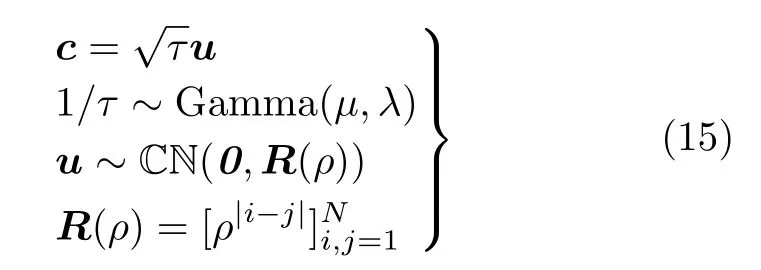
其中,G amma(µ,λ)表 示尺度参数µ 、形状参数λ 的Gamma分布,C N(0,R(ρ))表示0均值、协方差矩阵为R (ρ)的 复高斯随机向量,ρ 为协方差矩阵的结构参数。由式(14)可知,虚警率与某参数无关时,相应的CFAR检测门限也与该参数无关。本文使用蒙特卡罗实验得到广义Pareto分布海杂波背景下CACFAR和OS-CFAR检测器在不同参数条件下的检测门限。蒙特卡罗实验中,选取积累脉冲数N =10、参考单元数 P=40。由式(14)可知广义Pareto分布海杂波背景下,CA-CFAR和OS-CFAR检测器的虚警率与尺度参数µ 无关,即CA-CFAR和OS-CFAR检测器关于尺度参数 µ是恒虚警的。实验时为了方便,设置尺度参数 µ=1。对于OS-CFAR检测器,k取值30。

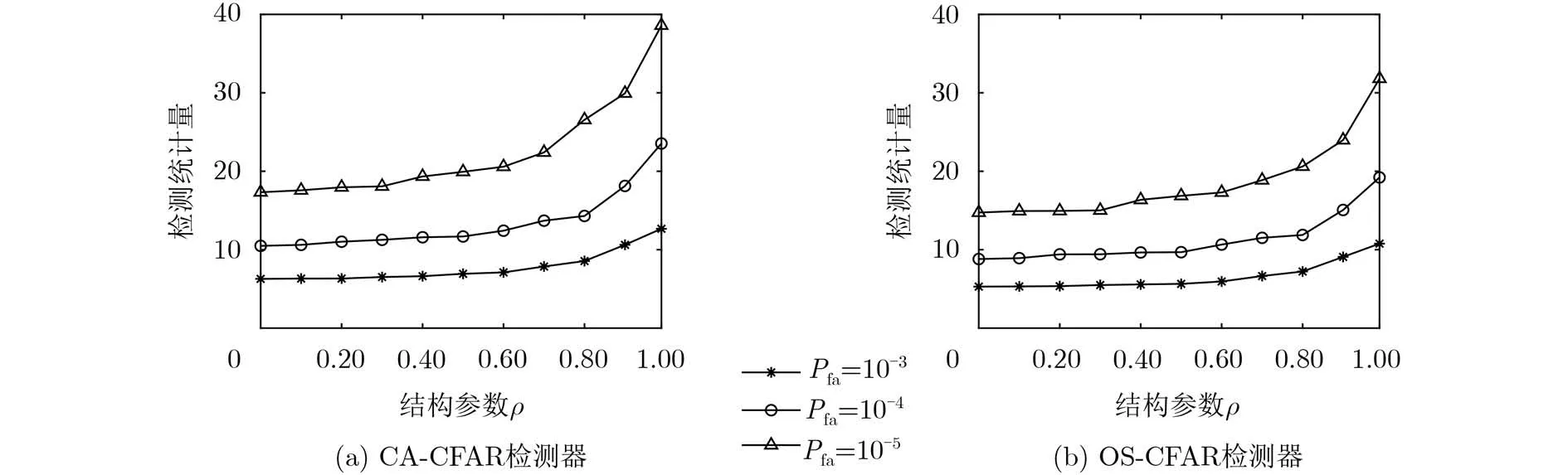
图2 CA-CFAR和OS-CFAR检测器的检测门限随着散斑协方差矩阵结构参数的变化情况
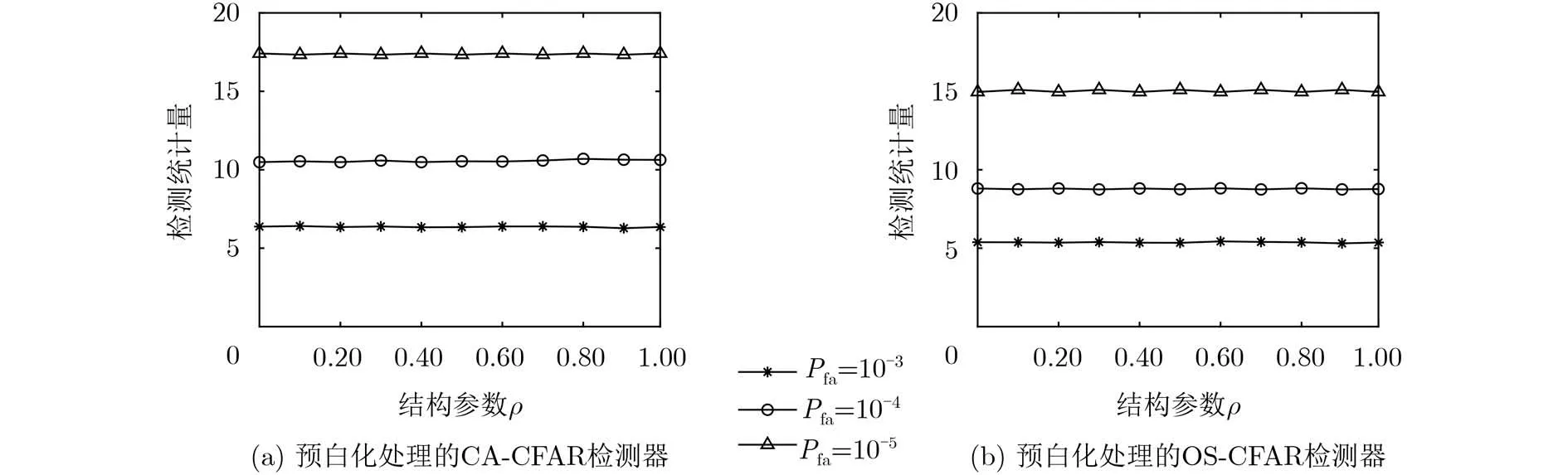
图3 预白化处理的CA-CFAR和OS-CFAR检测器检测门限随着散斑协方差矩阵结构参数的变化情况
第2个实验:验证两种非相干检测器的检测门限与广义Pareto分布海杂波的形状参数 λ之间的关系。形状参数 λ从1~20取值,间隔为1;散斑协方差 矩 阵 结 构 参 数 ρ=0 和ρ =0.9 ;虚 警 率Pfa取 值10−3, 10−4, 10−5。实验结果如图4所示。当虚警率和散斑协方差矩阵结构参数一定时,随着形状参数的减小,两种检测器的检测门限变大。这是因为形状参数越小,海杂波的非高斯性能越强,杂波幅度分布的拖尾越严重,检测门限越大,这说明了两种检测器的检测门限与形状参数有关,即两种检测器关于形状参数是非CFAR的。为了保证全场景CFAR检测,应该使用匹配形状参数的检测门限。另外,这一现象也说明了在海杂波的非高斯性能变化的大场景下应用非相干检测器检测目标时,传统的固定检测门限的非相干检测器会产生严重的性能损失。当虚警率和形状参数一定时,两种检测器在ρ=0 时的检测门限大于ρ =0.9时的检测门限,这一现象反映了两种检测器关于杂波散斑协方差矩阵是非CFAR的,再次说明了在相参雷达中目标检测前对雷达回波进行白化处理的必要性。
3.2 实测数据检测性能分析
接下来,采用实测海杂波数据评估全场景CFAR的CA-CFAR和OS-CFAR检测器的检测性能。本节使用的3组实测数据是C波段的Fynmeet雷达在南非采集到的海杂波数据[15],雷达载频6.9 GHz,距离分辨率15 m,脉冲重复间隔fr=5000 Hz。第1 组数据C F A 1 6_0 0 3.0 1.m a t、第2 组数据CFA16_005.01.mat和第3组数据CFA16_017.01.mat均由96个距离单元和67334个相干脉冲构成。该3组数据的幅度图如图5所示,使用广义Pareto分布拟合3组数据的海杂波幅度分布,拟合结果如图6所示,其中点迹表示海杂波数据幅度的经验概率密度曲线,黑色实线表示广义Pareto分布拟合曲线。3组数据幅度分布的广义Pareto分布拟合 结 果 的 参 数 分 别 为: λ=2.7822 , µ =1.0253;λ=3.7894 , µ =0.3358; λ =6.3212 , µ =0.3908,其中 λ是形状参数,µ 是尺度参数。由图6可以看出,广义Pareto分布模型能够很好地描述该3组数据。在3组实测海杂波数据中加入仿真目标,分析全场景CFAR的CA-CFAR和OS-CFAR检测器在不同信杂比(Signal-to-Clutter Ratio, SCR)情况下的检测性能。在一个相干处理时间内,目标回波信号可以建模为目标回波复幅度和多普勒导向矢量的乘积
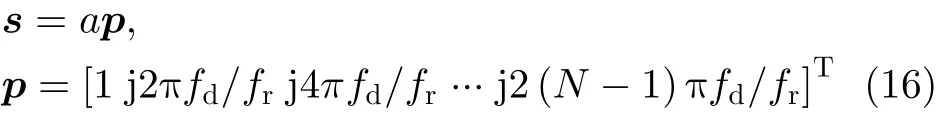

图4 CA-CFAR和OS-CFAR检测器的检测门限随形状参数的变化情况

图5 3组数据的幅度图
其中, a 是目标信号的复幅度,fd是目标多普勒频移, fr是脉冲重复频率,p 为多普勒导向矢量。在实验中,目标多普勒偏移在区间[ −fr/2,fr/2]中随机选取。目标回波的SCR定义为S CR=10 lg(|a|2/),其中,是海杂波的平均功率水平。
基于球不变随机向量模型,检测器通过待检测单元周围的参考单元数据估计杂波的散斑协方差矩阵,进而完成杂波白化。为了保证检测器的性能损失小于3 dB,通常参考单元数P与积累脉冲数N满足P≥2N[19]。然而,3组数据相干脉冲数高达67334个,而距离单元数目仅有96个,无法获得足够与待检测单元具有近似或者相同散斑协方差矩阵的参考单元。针对该问题,采用块白化方法在目标检测前对杂波进行白化。将待检测单元向量z和参考单元向量zp分别截为长度为N的不重叠的短向量wl和wp,l,满足条件P≥2N
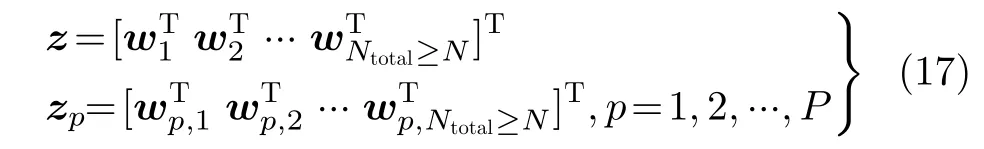
其中,Ntotal是总的相干脉冲数。采用归一化采样协方差矩阵(Normalized Sampled Covariance Matrix, NSCM)估计方法,从第l块的参考单元数据中估计第l块的杂波散斑协方差矩阵

在实验中,脉冲积累数 N =10,参考单元数P =40 ,保护单元数目Q =2 ,虚警率Pfa=10−4,目标SCR的值从0~30 dB均匀选取,间隔为2 dB,检测门限通过查表方法获得。分别在3组数据中加上仿真目标进行了105次独立试验,获取全场景CFAR的CA-CFAR和OS-CFAR的平均检测概率。两种检测方法在不同SCR情况下的平均检测概率如图7所示。由图7可以看出,在3组数据中,OS-CFAR的检测性能整体上优于CA-CFAR,这是因为3组数据中存在一定异常单元。在高分辨对海雷达中,海杂波表现出强非高斯性,杂波中含有大量类似目标的尖峰回波并且海场景中可能存在岛礁,因此海杂波中的异常分辨单元通常是不可避免的。因此,在实际海杂波环境中,OS-CFAR检测方法的检测性能通常较好。
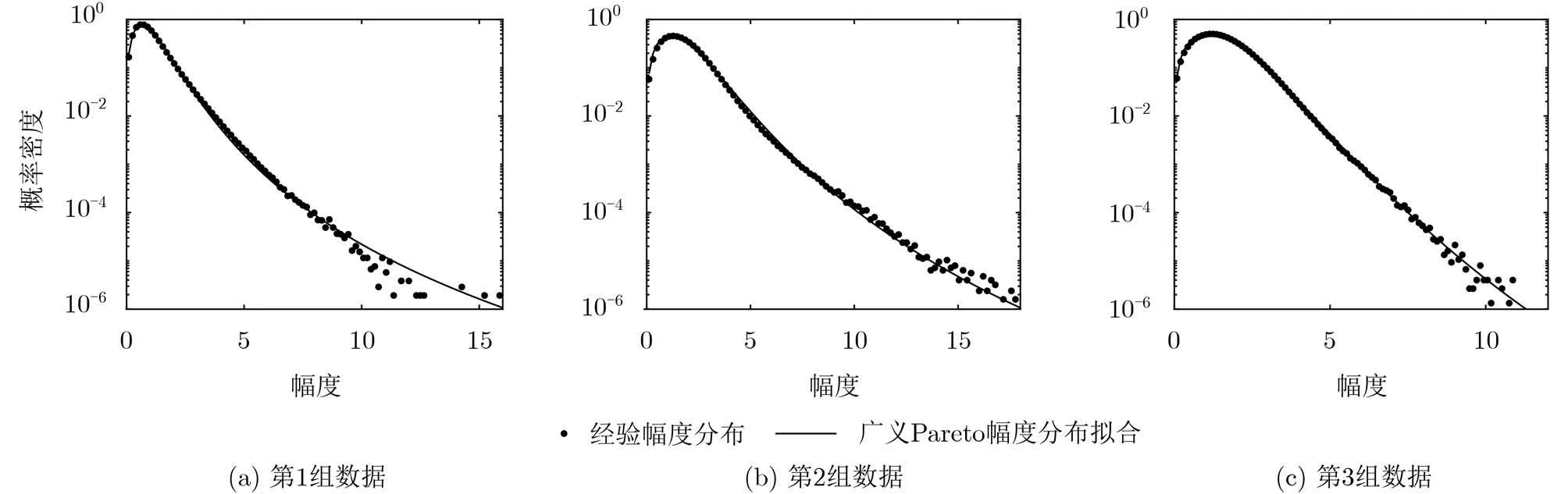
图6 3组数据的幅度分布拟合结果

图7 全场景CFAR的CA-CFAR和OS-CFAR检测器在3组数据不同目标信杂比情况下的检测概率
4 结束语
本文主要研究了广义Pareto分布海杂波背景下CA-CFAR和OS-CFAR两种非相干检测器的CFAR特性。理论分析表明,两种非相干检测器关于杂波功率是CFAR的。为了保证全场景的CFAR检测,在检测前对雷达回波白化处理以保证非相干检测器关于杂波散斑协方差矩阵的CFAR特性,与此同时基于查表方法应用了匹配杂波形状参数、脉冲累积数和参考单元数的检测门限以保证非相干检测器对这3个参数的CFAR特性。实验结果表明,CA-CFAR和OS-CFAR检测器能保证全场景CFAR特性。
