经历探索过程 感受演绎推理——拓展课《数字在哪里》教学实录与思考

□覃佳韵

推理广泛存在于人们的生活中，而且贯穿于各个学科的学习中。数学本身是一门逻辑性极强的科目，数学教学与学生推理能力的培养密不可分。受小学生年龄特征、认知水平所限，小学数学中与推理相关的内容往往是多合情推理，少演绎推理。

人教版教材二年级下册在“数学广角”中安排了一节演绎推理的“入门课”。实践表明，学生在低年级已经能理解简单的演绎推理过程，能运用一些推理的方法进行思考，并且能用简单的数学语言进行表达，但教材中没有作更深入的内容安排。为进一步提高学生的演绎推理能力，笔者设计了一节基于培养推理能力，以在九宫格中填数字为主要内容的拓展课《数字在哪里》，让学生在愉快的游戏过程中经历演绎推理的过程。

【教学过程】

（一）了解规则，形成共识

师：这是一个九宫格，三个小朋友分别“住”在其中的一个格子里（图1）。为了表述清楚，我们可以借助表格外的标注来表示他们的位置。比如小明的位置在上2，小强的位置在中1，小红的位置可以怎么表示？（生答）

图1

师：刚才我们帮三位小朋友找到了位置，现在我们来帮数字找位置。（出示课题：数字在哪里）

师：（呈现题目，如图2）你能看懂题目的意思吗？数字9和数字3要放在哪儿呢？

图2

生1：数字9 一定在中2 的位置上，数字3 不一定。

师：你有自己的想法，如果能说清楚你这样想的原因就更棒了。

生2：数字要放在标有“★”的位置上，所以9应该放在中2。数字不能在标有“×”的位置上，所以除了画“×”的位置以外，3 在上3、中1、下2 这三个位置都有可能。

师：厉害！同学们有没有注意到，刚刚生1 回答的时候用了“一定”“不一定”，非常清晰地告诉我们他判断的结果，而生2 用了一组词——“因为”“所以”表达了自己判断的理由，这些词能够帮我们说得更清楚，让别人听得更明白。

生3：可能在上1。

师：有这种可能，同学们，他为什么不说一定在上1？

生4：因为信息只告诉我们4 在一行的第一个位置上，九宫格有三行，所以有三种可能，也就是4可以放在上1，也可以放在中1，还可以放在下1（如图3）。

图3

小结：我们可以根据已知信息帮数字找位置。有些信息可以帮助我们准确地判断数的位置，有些信息不能让我们直接确定数到底在哪个位置，但能圈定范围，细心的同学会找出所有可能的答案。

生5：有两种可能，如果数字5在上2，那么数字9就在上3；如果数字5在上3，那么数字9就在上2。

小结：如果有两个数字、两个位置可供选择，那么这两个数字都有可能在其中的某一个位置上，只要确定其中一个数字的位置，另一个数字的位置也就随之确定了。

（设计意图：建立共识，是明确推理前提条件的过程。这一环节的设计重在与学生建立以下几条共识：第一，表达位置的共识。用上、中、下、1、2、3分别表示横行数列的位置，用统一的先行后列的方式表达数所在格子的位置，这是后面大家交流的基础。第二，表达思考的共识。鼓励学生用“因为”“所以”“可能”“一定”等词语表达思考的过程，这不仅是培养学生表达的习惯，更是培养学生思维的缜密性与严谨性。第三，基本逻辑的共识。“★”可以帮助确定数字所在的位置，“×”可以帮助排除数在某一个格子的可能。根据信息，有时可以直接得到答案，有时可以得到几种可能的答案；当两个数可以选择AB两个位置的时候，一个确定了，另一个也随之确定。）

（二）演绎推理，经历过程

1.小试牛刀

（1）呈现问题，请学生独立尝试解决。

在九宫格里放入1、2、3、4、5、6、7、8、9，每格放1 个数字，不能重复。数字在标有“☆”的位置上，数字不能在标有“×”的位置上（如图4）。

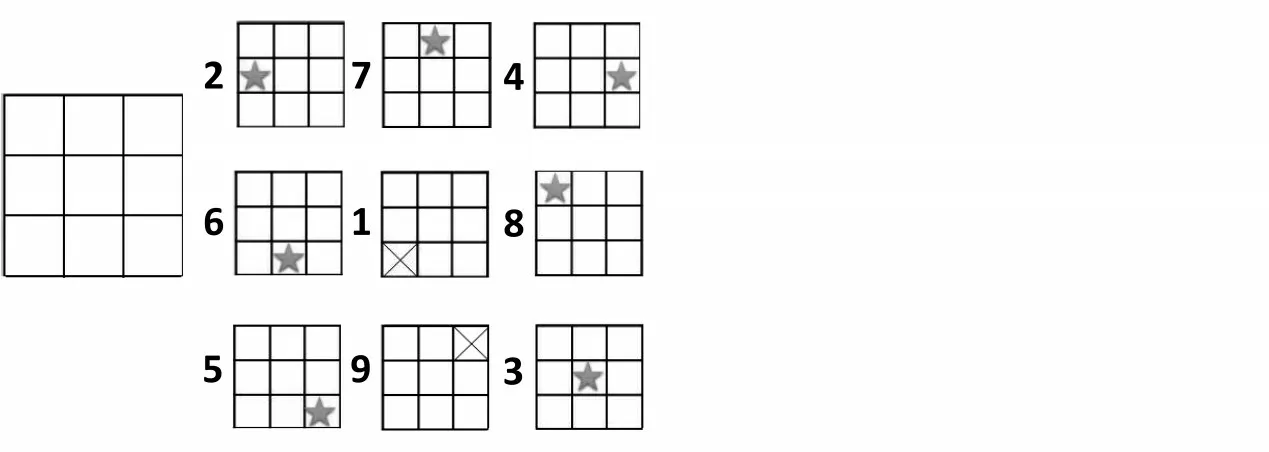
图4

（2）引导交流。

师：谁来说一说，根据信息提示，你是怎么填的？

生：因为“★”可以确定数字的位置，所以2、7、4、6、8、5、3 的位置都可以直接确定下来。先把这几个数字填好，然后只剩下1 和9 的位置，根据信息，1不能在下1，所以只能在上3的位置上，最后剩下的9在下1的位置。

2.挑战升级

（1）呈现问题，请学生独立尝试解决。

在九宫格里放入1、2、3、4、5、6、7、8、9，每格放1 个数字，不能重复。数字在标有“★”的位置上，数字不能在标有“×”的位置上（如图5）。

图5

（2）引导交流。

师：找到答案的同学，先检验一下，看看是不是可以保证自己的答案正确。然后想一想，怎么跟大家介绍你的思考过程。

生：我发现了一个秘密，这9 个数字旁边的格子，有的排除掉的可能性多，有的排除掉的可能性少。所以我就按照先填排除掉的可能性多的数这样的顺序填，就找到答案了。比如说，数字5 已经排除了8 个格子，它肯定在中1 的位置。数字2 排除了7 个格子，中1 填了5，所以2 一定在上3 的位置，这样很快就找到了所有的答案。

生：这道题看起来挺吓人，其实一点也不难，只要找到突破口，也就是先找只留有一个位置的数字来填就行了。

取能见度为1 km，平流雾和辐射雾的谱分布如图1所示.由图1可知，当能见度为1 km时，随着粒子半径的增加，两种雾的谱分布曲线均先增加后减小，且两种雾的浓度在半径较小一侧迅速增大，在半径大的一侧则缓慢减小.其中平流雾的雾滴粒子半径较集中在2～5 μm，辐射雾的雾滴粒子半径较集中在0.1～2 μm，且辐射雾粒子浓度约大于平流雾粒子浓度两个数量级.

（设计意图：同样是填9个数，本题从单一条件推理进阶到关联推理，让学生感受到只有当确定唯一可能的时候，才能直接确定答案。很多数看起来无法确定位置，但当确定了某一个数的位置以后，就等于给其他数的位置多“排除”了一种可能。）

3.灵活运用

（1）呈现问题，请学生独立尝试解决

在九宫格里放入1、2、3、4、5、6、7、8、9，每格放1 个数字，不能重复。数字在标有“★”的位置上，数字不能在标有“×”的位置上（如图6）。

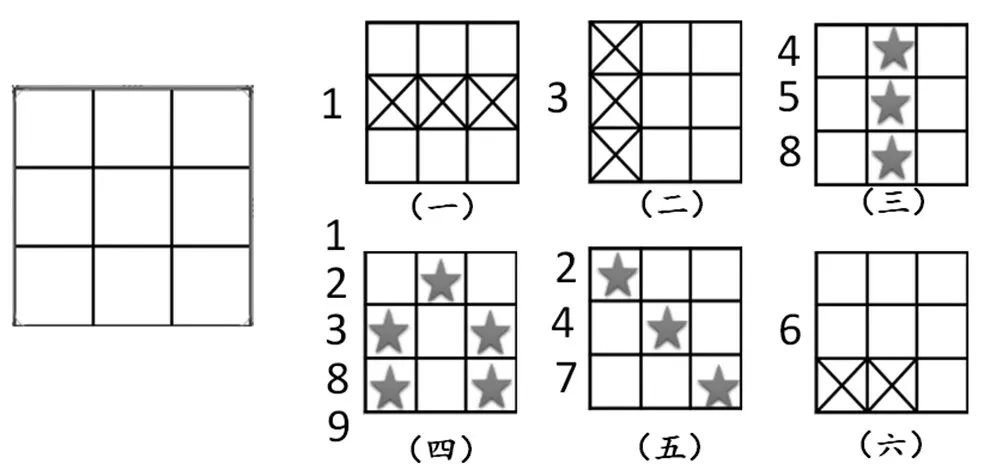
图6

师：没有“★”帮助我们直接确定某一个数，也没有8个“×”帮助我们排除所有可能直接找到某个数的位置，在这种情况下，你能想办法确定一个数的位置吗？先自己试试看。

（2）引导交流。

生：我可以确定数字4的位置。因为我看到图（三）和图（五）都有数字4，两幅图里的三颗星星中都有一颗是在中2 的位置，说明这就是数字4 的位置。

师：图（三）和图（五）还有数字5、8、2、7，为什么不是它们呢？

生：因为它们不是同时出现，只有数字4 两幅图里都有，所以星星重叠的位置，就是数字4 的位置。

师：通过观察两幅图中同时出现的数字，推理出星星重叠的位置就是这个数字的位置。按照这个思路，还能找出哪个数字的位置？大家可以拿出桌面上袋子里的小帮手，摆一摆，你还能找出哪些数字的位置？

……

小结：数字的位置不能唯一确定的时候，可以将几幅图的信息整合在一起找到突破点，再利用排除法、重叠法等方法来推理出数字的位置。

（设计意图：本题从关联推理进阶到多个条件复合推理，对学生来讲，思维更有挑战性，实际教学中学生对本内容的兴趣非常浓。他们在独立尝试与合作交流的过程中逐步体会，当根据一个条件不能直接确定答案的时候，可以将两个甚至几个条件复合起来进行判断，找到数字位置。引导学生用“根据满足……又满足……可以确定答案”的方式进行表达，更深刻地体会推理的严谨性。）

【教学思考】

（一）演绎推理教学有必要从低年级开始

数学教学内容的学习与推理能力的培养密不可分。《义务教育数学课程标准（2011 年版）》中提出了小学数学的10 个核心词，反映了对小学生数学素养的基本要求，其中就包含了推理能力。但小学数学的教学中，无论是教材编写还是教师教学，对推理尤其是演绎推理的教学都不够重视。虽然小学生掌握的知识有限，认知能力发展还不够完善，但他们正处在思维发展的重要奠基阶段，从低年级开始，逐步培养科学严谨的思维方式，养成“言必有据，说必有理”的习惯非常重要。因此，演绎推理教学有必要从低年级开始进行。

（二）演绎推理教学有可能从低年级开始

在人教版教材二年级下册关于演绎推理的“入门课”教学中，教师会感受到学生有进行演绎推理的可能，他们能够理解根据前提推导出结论的过程。本节拓展课的教学，学生经历的演绎推理过程层层深入。在初步建立共识以后，学生先后经历根据单一条件进行演绎推理、关联推理、复合推理几个阶段，每个阶段中学生都先独立思考，尝试解决问题，然后在教师的带领下通过相互交流，学会有根据有条理地表达推理过程，体会有逻辑的思考、有逻辑的表达。学生情况不同，在一节课里能够落实的程度必将不同，本节课的教学在一些班级的实践中取得了很好的教学效果，但这并不说明这样的教学内容或层次设计可以在任何一个课堂里进行。教师可以根据学生的实际情况选择本节课的终点，但无论学生可以进行哪一个层次的逻辑推理，实践表明，演绎推理的教学可以在低年级进行。