一种基于MATLAB 的航天产品生产齐套方案的优化方法

杜博迟 臧梓轶 李昞晖 王国星 胡亚航 蔡朝阳

北京卫星制造厂有限公司 北京 100094

环控生保（环境控制和生命保障）分系统的使命是在外太空创造一个适合人类生活和居住的环境,直接保证航天员的安全、健康，同时也保证飞行器平台上一些功能的实现。该分系统构成分类如表1 所示。

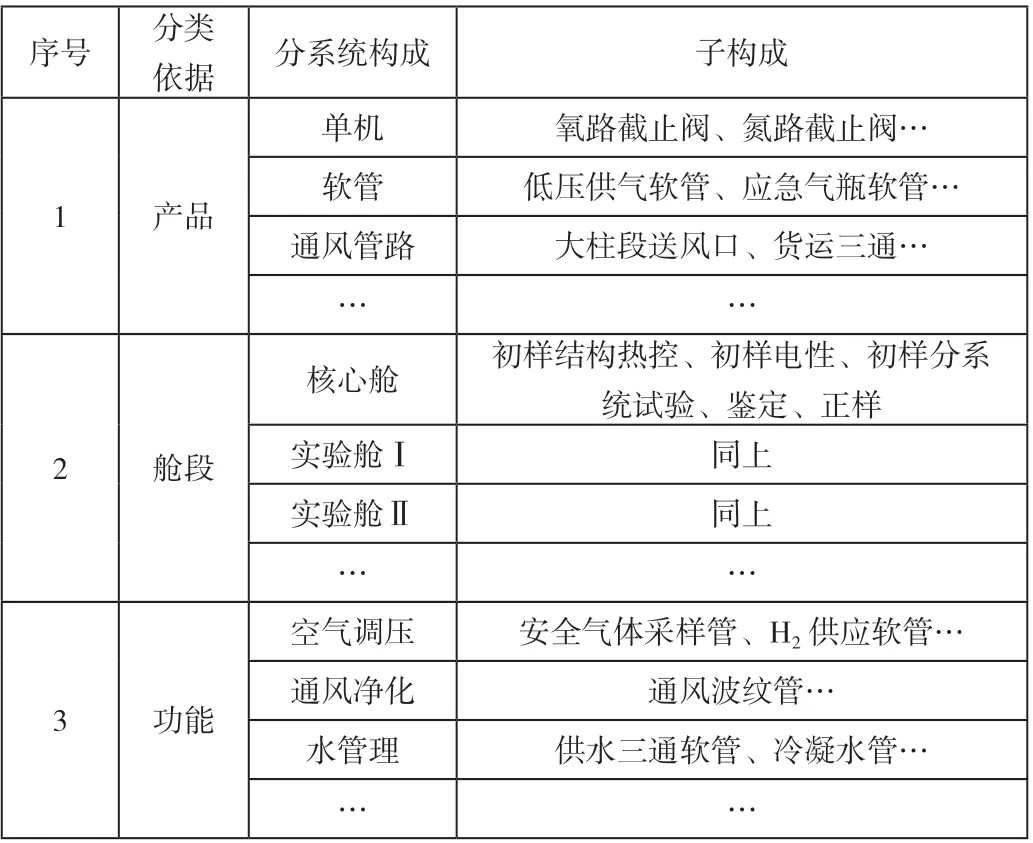
表1 分系统构成分类

图1 一些软管产品实物图

（1）配套需求大。三舱均有配套，每个舱段存在五种研制状态，每种状态均需交付100 余件产品，产品研制总量1500 件左右。

（2）设计个异性。主要由接头、管体、密封圈等构成，由于舱段接口个异性，故接头设计也存在个异性，一种研制状态包含80 余种零件，耦合情况复杂。

（3）节点进度紧。管路的研制周期如表2 所示。此外还需对产品材料特性（如毒性）进行试验，周期很长。

（4）齐套难度高。由表2 可以看出时间占比最长的项目是零件生产，同时密封圈等标准件是外部采购的，受供货方制约，齐套难度很高。

通过分析可以看出，目前产品存在复杂的耦合情况，在零件库存不足的情况下，很难通过手动计算提出一种满足最大交付能力的分配方案。

1 建立数学模型

假设用户提出一批软管产品的交付要求，经分析，目前库存零件不能满足本批产品交付能力，需要乙方提出一种交付方案使交付产品数量总和最多[1]。

表2 软管产品研制周期表

1.1 建立代数模型

需要交付产品的数量定义为W，W=[W1,W2,W3…Wn]，n 为产品种类数量，即向量维度。零件实体库存数量定义为T，T=[T1,T2,T3…Tm]，m 为零件种类数量，实际可交付的产品数量为X，在完成一次分配后零件实际消耗数量为Y。产品及零件配套关系如表3 所示。

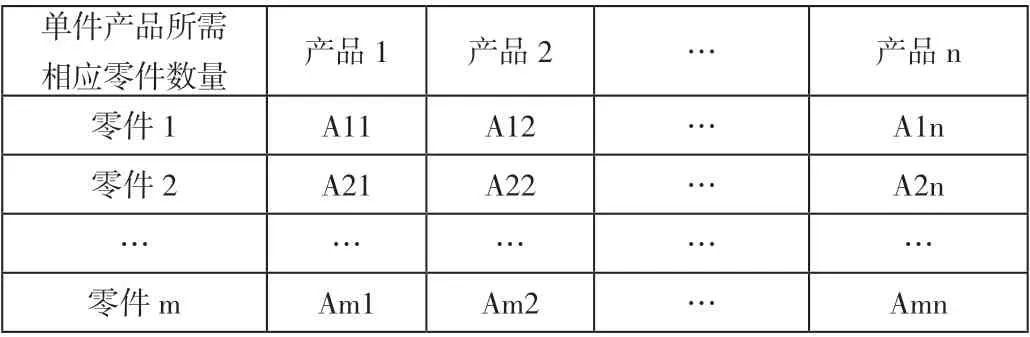
表3 产品、零件配套表

其中Amn 表示每件产品n 成型需要零件m 的数量。

1.2 建立约束

（1）产品数量为整形自然变量（int8）[0,inf](inf 表示无穷，此处不考虑上限)，故Xi ≥0，i=1：n。

（2）由于我们解决的问题是库存零件不足时产生的分配问题，故Xi ≤Wi，i=1：n。

（3）在完成一次分配后零件使用情况满足以下条件：

（4）根据用户需求，假设指定某几项产品的交付数量，则Xi=constant（i），i 和constant（i）由用户指定。

1.3 建立目标函数

本文研究面向用户的目标函数，实现交付产品数量最多的目标，公式如下：

式中fval 表示目标函数值。

2 基于MATLAB 的线性规划算法

根据模型可以看出，问题可以归纳为线性约束条件下的极值求解，本文利用MATLAB 中的fmincon 算法实现。

2.1 算法介绍

fmincon 是用于求解线性&非线性约束条件下多元函数最小值的MATLAB 算法，语法格式如下：

[x,fval,exitflag]=fmincon(fun,x0,A,b,Aeq,Beq,lb,ub)

其中，x 为变量，fval 为目标函数值，exitflag 为循环溢出标志返回值，fun 为目标函数，，x0 为初值，A 为线性不等式约束系数矩阵，b 为线性不等式的约束值，Aeq 为线性等式约束系数矩阵，Beq 为线性等式的约束值，ub、lb 为变量的上、下界向量。

2.2 编译目标函数程序

2.3 数据传输

在excel 中加载Excllink，建立与MATLAB 的数据连接，在excel 中进行章节2.1 的数值输入，将数据传递给MATLAB 中的变量单元。通过excel 输入的优点是：

（1）表格数据库录入、修改、维护方便；

（2）空值默认补“0”；

（3）计算结果在excel 中传输方便。

2.4 优化计算

本例中参数建立传输完毕后，直接利用函数fmincon 进行计算。程序为：

lb=zeros(length(x),1);%建立一个与x 长度相同的（n 维）n行1 列的零矩阵

x0=ones(length(x),1）;%建立一个与x 长度相同的（n 维）n行1 列的一矩阵

[x,fval,exitflag]=fmincon(@mysum,x0,A,b,Aeq,Beq,lb，[])

ub 无限制，用[]，x0 为初值，为避免无解，不建议从全零矩阵开始，初值选择的不同，最后计算的结果可能不同，在后面讨论。

2.5 数据处理

由于MATLAB 默认为double 浮点型数据，故变量x 的解为浮点型数据，整数解应出现在最优解附近。MATLAB 中变量取整提供三种函数，分别是ceil(x)，向正无穷取整；floor(x)向负无穷取整；round(x)，四舍五入取整。分析目标函数可以知道，fval 关于x 呈正相关，x 的每一个分量越大，fval 越大，在三种取整方式中，ceil ≥round ≥floor。需要将变量代入约束条件确认溢出情况，如解不合适，需要循环减小变量取值[2]。

3 应用实例

以某舱段4 种软管产品为例，配套情况如表4 所示：

设需交付的产品为CO2解吸软管2 件，微量解吸软管2 件，CO2排放软管3 件，CO2供应软管3 件，故W=[2,2,3,3]′，实体库存中每种零件均有25 件，故T=25＊ones(10,1)，实际可交付的产品数量为x，是一个4 维向量，在完成一次分配后零件实际消耗数量y 是一个10 维向量，用户指定CO2排放软管要全部交付，故x(3)=3。根据章节2.2 可列出约束不等式组：

表4 产品配套表

分析x 的值可以看出，产品1、2、4 在1.0833 时函数取得极值，对变量取整，每个小数总存在向左、向右两种取值方式，在所有的取值情况中ceil(x)＞round(x)=floor(x)，利用零件消耗量y 判断是否溢出，可以得到最优解为x=[1,1,3,1]′，选择不同的初值进行计算，得到的结果完全相同。即CO2解吸软管可交付1 件，微量解吸软管可交付1 件，CO2排放软管可交付3 件，CO2供应软管可交付1 件，本批可交付软管产品6 件，为目前最大交付能力，满足假设条件[3]。

4 结语

利用MATLAB 中自带的优化函数fmincon，可以很好地解决多零件耦合方案优化问题，计算准确、快速到位，同时利用excel进行数据库的管理工作，数据录入、编辑、维护、采集都十分简便，效率得到了提升。随着卫星批量化需求的日益增强，生产线建设也正在面临着高效性方面的挑战。根据价值流分析可以看出，零件的齐套性是制约生产线高效运转的主要爆点，在整个装配领域都是一大痛点，传统方法主要依靠“人员调度”，进行资源优先级分配，但当产能拉伸扩大后，人员干预不再能做出最佳方案选择，本文研究的实质为利用动态线性规划，目标函数最优方案解算，可以很好地解决这个问题，具有重要的推广意义。后续主要研究方向为零件加工的复杂性对生产周期、成本、加工成功率的影响，如图2 所示。目标函数的建立应包含用户需求、利润、周期、成本和加工成功率等多个维度，很可能进行非线性约束条件下的极值求解，所以目标函数的编程是一个重要工作。

图2 产品复杂程度与生产周期、成本、加工成功率关系示意图