基于斜盘交错角的柱塞泵流量脉动研究∗
2021-04-04
(西南交通大学机械工程学院 成都 610031)
1 引言
为了降低斜盘式轴向柱塞泵的噪声,必须减小来自泵源处的流量脉动和振动,控制流量脉动的关键因素在于配流盘的设计,配流盘上的腰形槽的开启角度和关闭角度对流量脉动、柱塞腔冲击力、斜盘力矩有着重要影响[1]。靠增加出口腰形槽的开启角度,即形成预压缩角,使柱塞在运动过程中对油液进行预压缩,可以使柱塞腔与出口腰形槽连通时的油压与出口压力完美匹配,从而减少由油液压缩性带来的流量脉动[3]。但是预压缩角的缺点在于对工况的高敏感性,即当出口压力、转速、排量角发生变化时,流量脉动将会增加,配流盘腰形槽不再是最优设计[2]。文献[4]依靠旋转配流盘的方法来调节配流盘的开启角度[4],使得预压缩效果与工况相匹配,这种方法的缺陷在于实现成本较高而且需要外部设备进行实时调节,不便于推广应用。而斜盘交错角结构通过调节斜盘的交错角来改变柱塞的运动规律,等效于旋转配流盘且实现成本较低,是一种较好的降低流量脉动的方式。
如图1所示,虚线表示柱塞泵斜盘的法向量,用来确定斜盘的空间朝向,传统的斜盘转动方向是绕Y轴旋转,而交错角结构的斜盘是先绕X轴旋转交错角α,斜盘法向量由OZ转动到OA,再绕Y轴旋转排量角β,斜盘法向量由OA转动到OA'。通过两次转动使斜盘与配流盘之间形成一个错配角,等效于旋转配流盘改变柱塞的运动规律,从而影响柱塞在三角槽过渡区的压缩体积,进而减小倒灌流量、降低流量脉动率[5~7]。
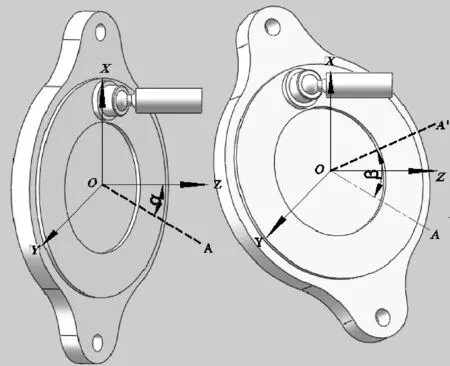
图1 斜盘交错角原理
2 柱塞的运动分析
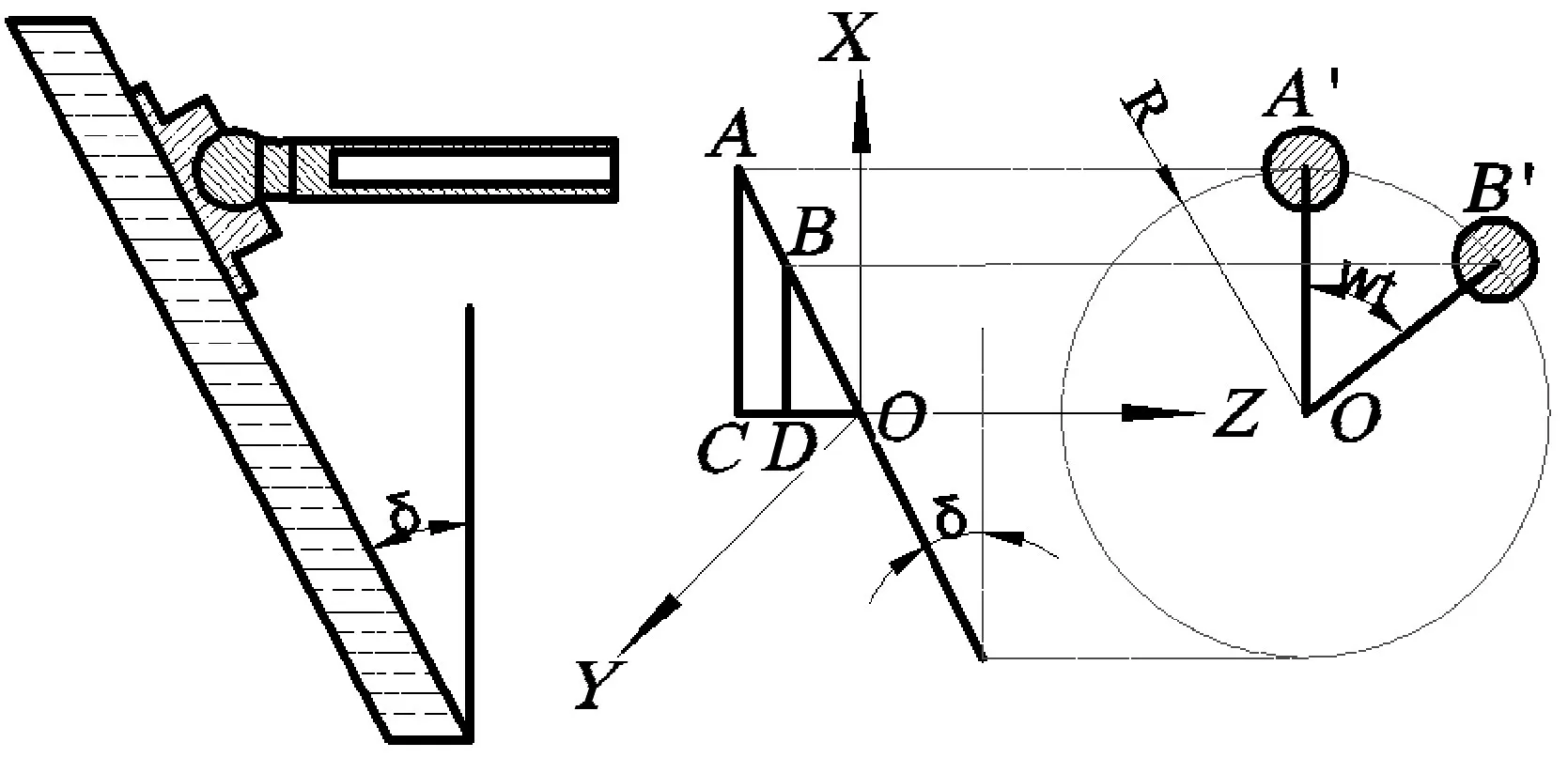
图2 柱塞运动原理
要分析交错角对柱塞运动的影响,首先要分析一般柱塞泵的柱塞运动规律,在此基础上考虑交错角对柱塞运动规律的影响。
如图2所示,以斜盘的中心O点为坐标系原点、柱塞在X方向上的最高点A点为柱塞开始运动的起点,则柱塞的运动轨迹在X-Y平面上的投影是一个圆,该轨迹圆在X方向上的位移为

由于柱塞在Z方向上的位移与X方向上的位移成正比,比例为斜盘倾角的正切值:
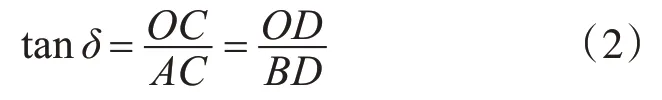
式中AC与BD是X方向上的位移,OC与OD是Z方向上的位移。
所以柱塞在Z方向上的位移即轴向位移等于X方向上的位移乘以tanδ,即:

该余弦函数的相位角为0,当且仅当斜盘的旋转轴为Y轴时成立。若斜盘存在交错角,则无法确保斜盘的旋转轴是Y轴,斜盘可能绕X-Y平面内任意一根轴旋转。如图3所示,两条相互垂直的虚线分别表示斜盘的死点轴和等效旋转轴,斜盘的死点轴与配流盘的对称轴之间错开一个角度,即错配角ε。由于柱塞运动的起始位置位于配流盘对称轴,所以柱塞位移起始相位等于错配角ε,交错角柱塞泵的柱塞位移函数为
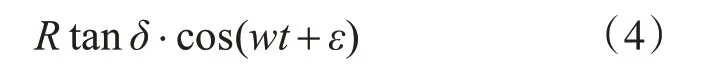
式中,R为柱塞分布圆半径,mm;w为主轴转速,r/min;δ为斜盘的有效排量角,°;ε为斜盘的错配角,°。
式中Rtanδ是余弦函数的幅值,ε是余弦函数的相位角,只要能够计算出有效排量角δ与错配角ε就可以得出柱塞在轴向方向的运动规律,需要注意的是,此时的有效排量角δ不等于斜盘沿Y轴旋转的排量角β,有效排量角δ是以斜盘交错角α、排量角β为自变量的函数,同理错配角ε也是以α、β为自变量的函数[8]。
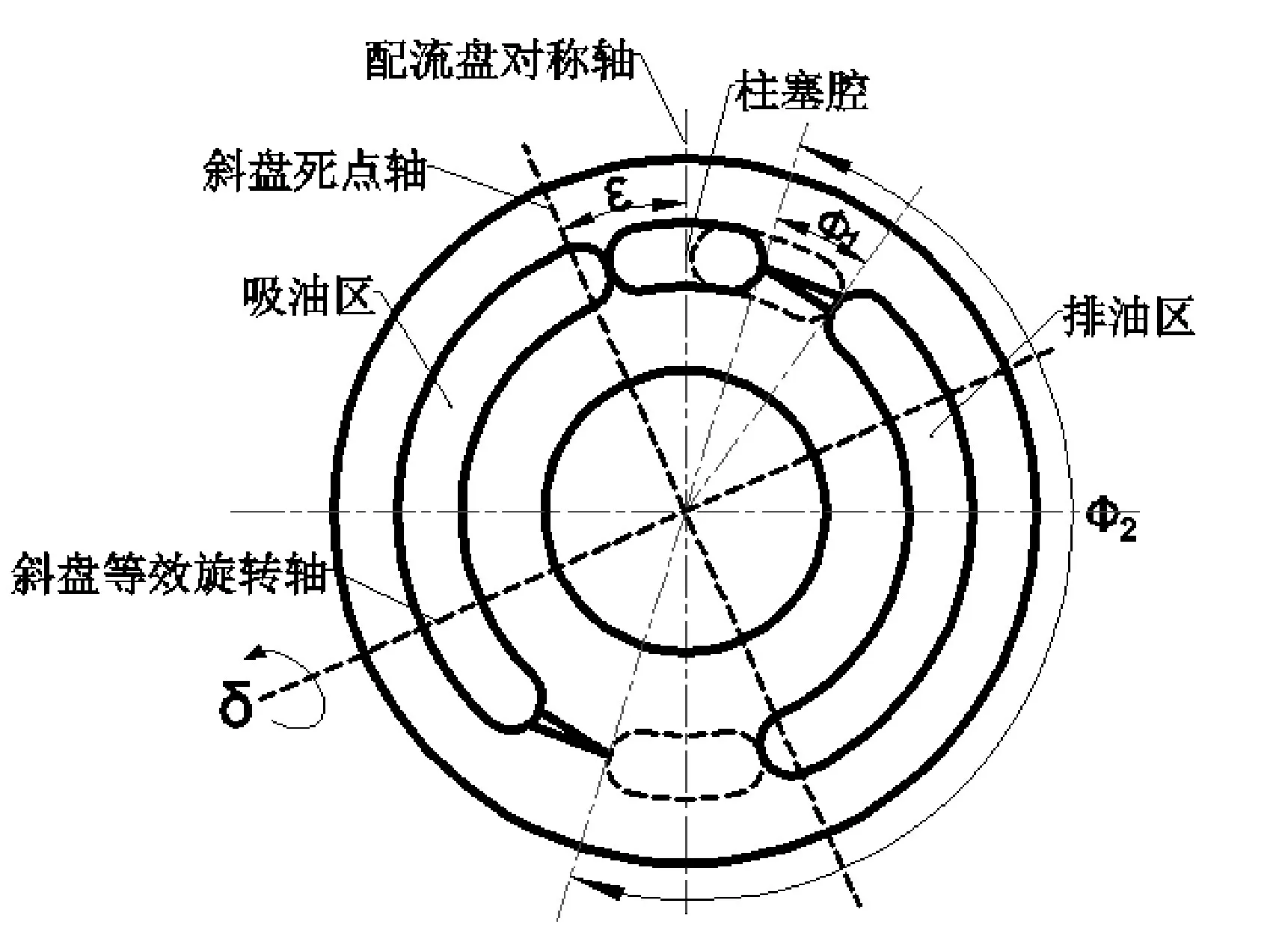
图3 交错角柱塞泵的柱塞运动规律
3 角度函数关系的几何分析
如图4所示,本文通过研究斜盘法向量的转动过程得出有效排量角δ、错配角ε与斜盘交错角α、排量角β的函数关系,为了方便数学描述,本文把斜盘法向量的转动过程放入到长方体内进行分析,假设O点为斜盘中心点,OZ为柱塞泵的主轴方向,初始斜盘法向量与OZ轴重合,斜盘法向量首先沿Y-Z平面转动α,由OZ轴转动到OA,再沿纵向平面XOA转动β,由OA转动到OA',通过两次转动,斜盘法向量的最终空间位置为OA',两次转动可以等效为一次在ZOA'平面上的转动,即法向量在ZOA'平面内由OZ转动有效排量角δ到OA',斜盘法向量的最终位置OA'在X-Y面上的投影即为死点轴,死点轴与配流盘对称轴(X轴)的夹角即为错配角ε,经过上述描述,将有效排量角δ、错配角ε、交错角α、排量角β放入到了四面体OAZA'中,下面通过数学推导得出有效排量角δ、错配角ε与交错角α、排量角β的函数关系。
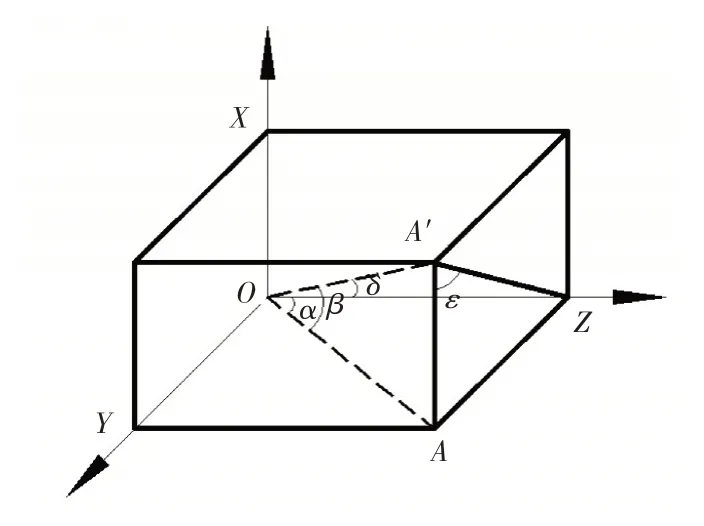
图4 斜盘法向量转动过程
1)δ与α、β的函数关系
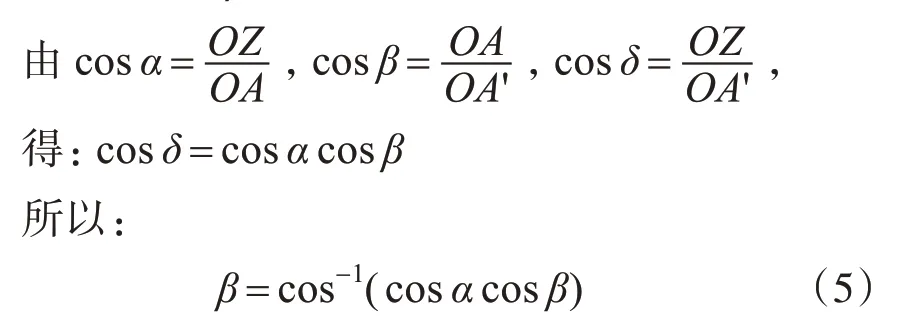
2)ε与α、β的函数关系
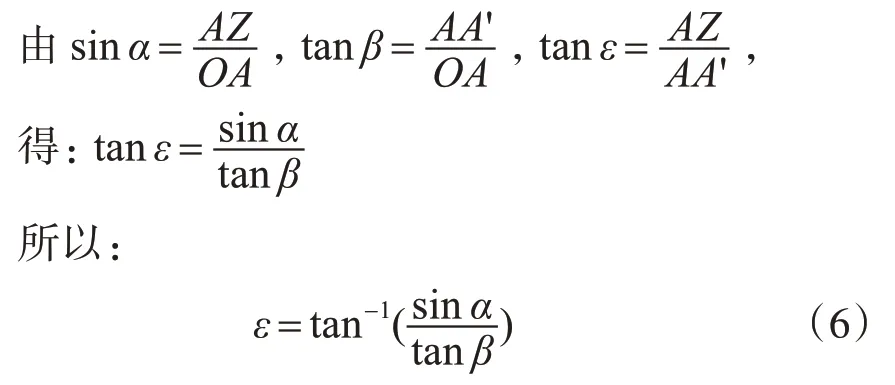
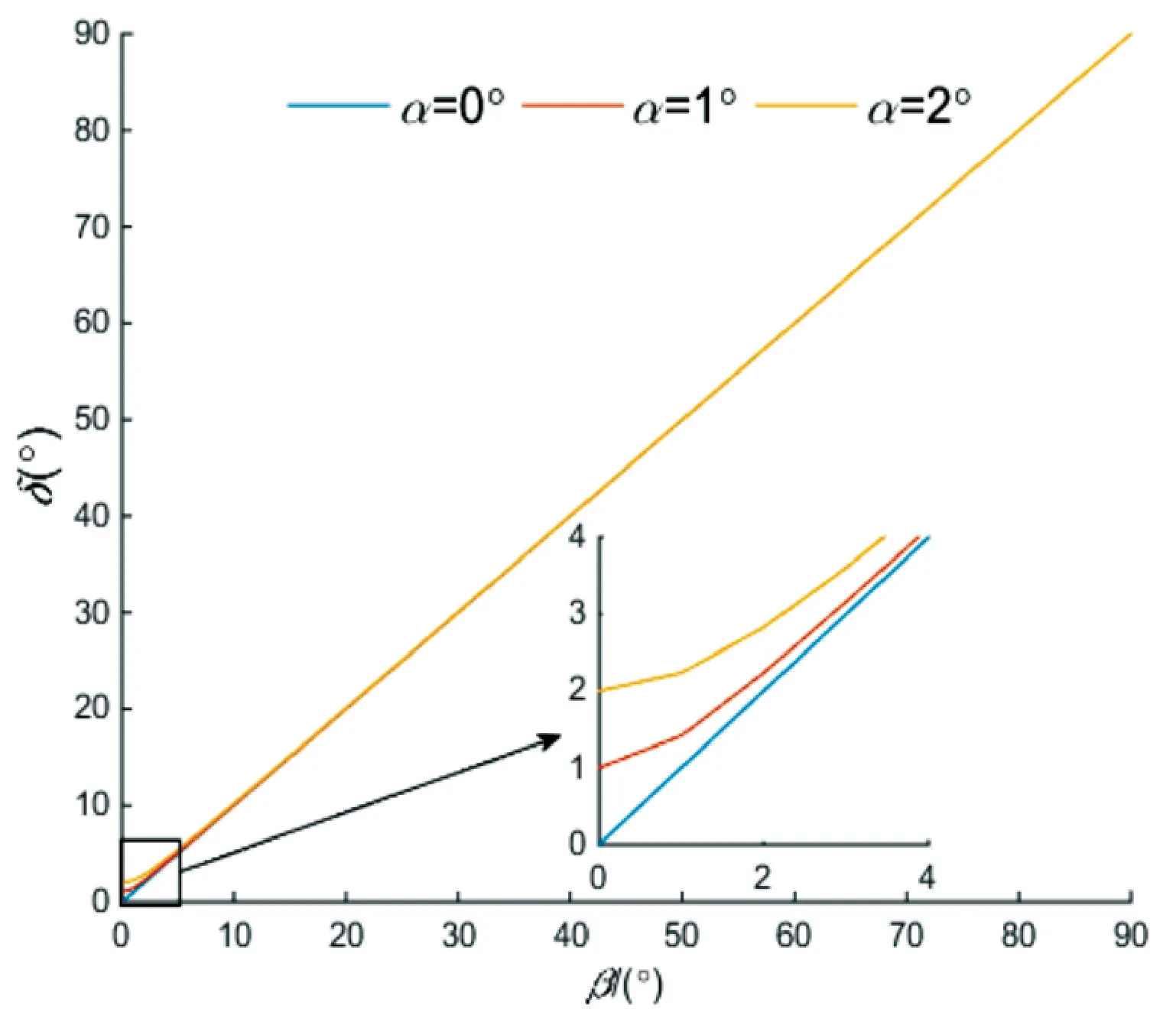
图5 有效排量角δ 与α、β 的函数关系图
斜盘的最大排量角通常在18°~20°之间[11],所以图5和图6中的排量角β的范围为0°~20°,本文采用的交错角α范围为-2°~2°[12],由于对称关系,图5、图6中的交错角范围为0°~2°。
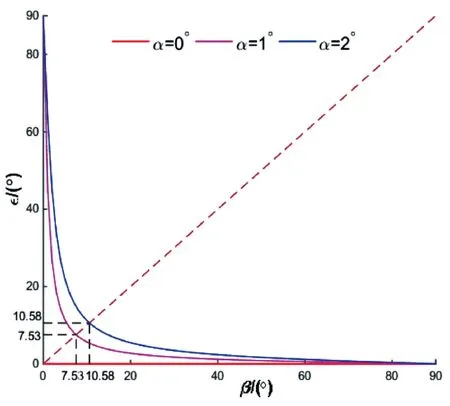
图6 错配角ε 与α、β 的函数关系图
由图5可知,斜盘的有效排量角受交错角的影响较小,且与排量角近似相等。这是因为通常情况下交错角较小,式(5)中的cosα近似等于1,将cosα≈1代入式(5)中得出δ≈β。所以在交错角较小的情况下,柱塞泵的有效排量角近似等于排量角。
由图6可知,斜盘的错配角与排量角的关系曲线近似于双曲线,该曲线相对于虚线ε=β对称。当错配角为1°/2°,曲线与虚线的交点为(7.53,7.53)/(10.58,10.58),当排量角由0°增加到7.53°/10.58°时,错配角由90°迅速降低到7.53°/10.58°;当排量角由7.53°/10.58°增加到90°时,错配角由7.53°/10.58°缓慢降低到0°。由此可见,随着排量角从0°增加到90°,错配角由90°下降到0°,且下降趋势是先快后慢。
4 柱塞压缩体积的数学分析
交错角通过改变柱塞的运动规律影响柱塞在过渡区的压缩体积和排油区的排量,过渡区的压缩体积和排油区的排量都与柱塞的轴向移动距离成正比,两者的区别在于包角大小不同[13]。如图3所示,三角槽过渡区的包角ϕ1为20°,而排油区的包角ϕ2为180°,下面通过数学分析得出任意包角的柱塞压缩体积的计算公式。柱塞的压缩体积公式为
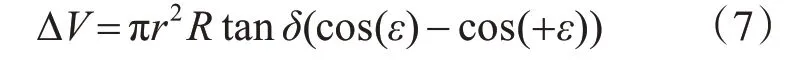
式中:r为柱塞半径,mm;ϕ为包角,°。
设ΔS=tanδ(cos(ε)-cos(ϕ+ε)),则:
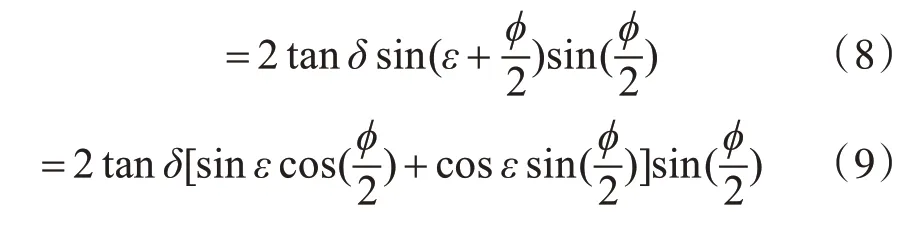
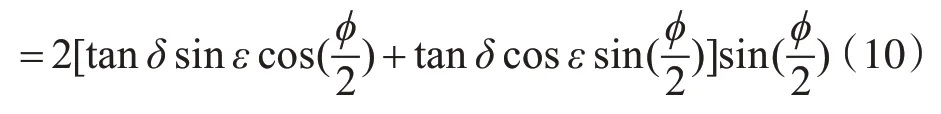
由图4中的几何关系可知:
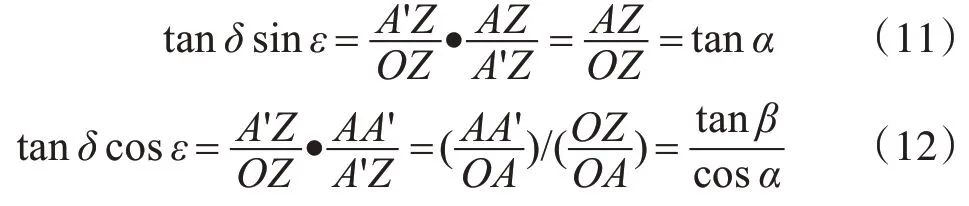
将式(11)、式(12)代入式(10)中,得:
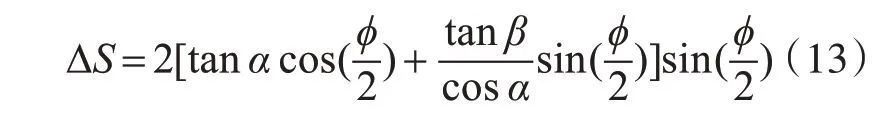
将式(13)代入到式(7)中,得:

式(14)是计算任意包角大小的柱塞压缩体积的一般公式,该公式中的自变量有三个,分别为交错角α、排量角β、和包角ϕ。如图3所示,三角槽过渡区的包角ϕ1=20°,排油区的包角ϕ2=180°,将ϕ1和ϕ2代入式(14)中,则三角槽过渡区的压缩体积为
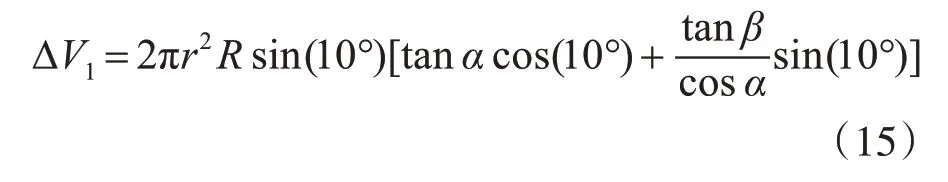
排油区压缩体积(单柱塞排量)为
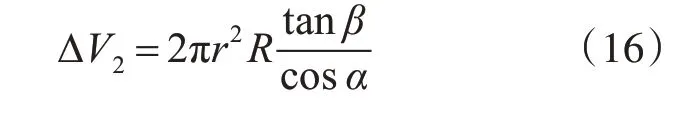
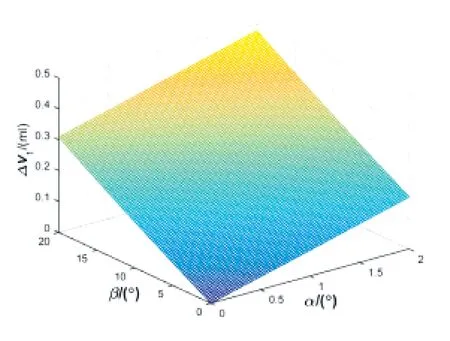
图7 三角槽过渡区压缩体积ΔV1与α、β 的关系
图7和图8是根据式(15)和式(16)得出的二维函数图,图中的排量角范围为0°~20°,交错角范围为0°~2°,从图8可以看出,交错角对排量的影响微乎其微,排量的大小主要跟排量角有关。从图7中可以看出,交错角和排量角都对三角槽过渡区的压缩体积有影响,图7近似为一平面,表示交错角和排量角可以近似线性改变过渡区的压缩体积,由图7可以看出,排量角每增加1°,压缩体积增加0.015mL,交错角每增加1°,压缩体积增加0.084mL,相较而言,交错角对于过渡区的压缩体积的影响比排量角更加显著。近似线性化后,三角槽过渡区的压缩体积公式可简化为
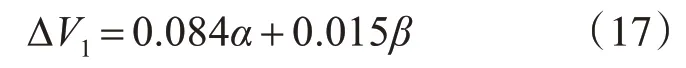
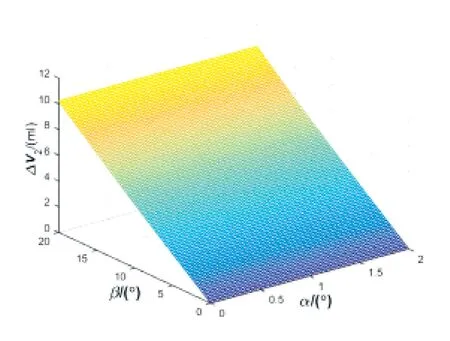
图8 单柱塞排量ΔV2与α、β 的关系
5 单柱塞腔的仿真
单柱塞腔的流量特性对整泵有重要影响,如图9所示,本文利用PumpLinx软件建立了一个柱塞泵的单柱塞腔仿真模型,柱塞腔的仿真参数[14]如表1所示。
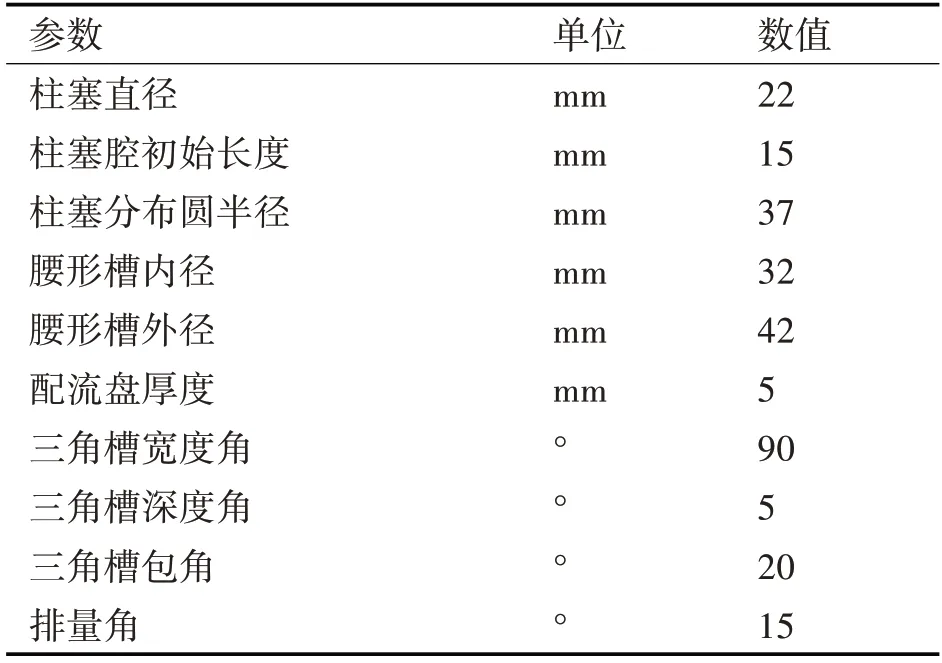
表1 仿真模型参数
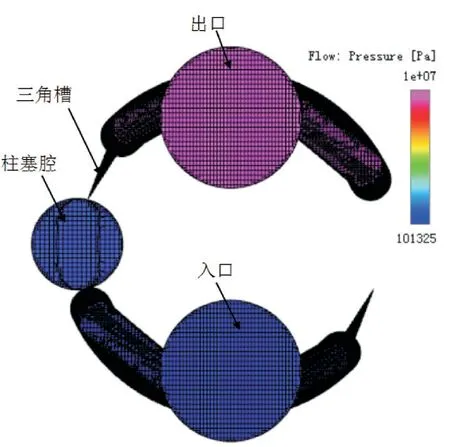
图9 单柱塞腔的仿真模型
几何流量:
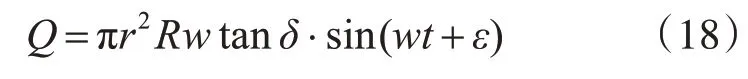
式(18)中的几何流量Q为正弦函数,其中r表示柱塞腔的半径,有效排量角δ与错配角ε都可以由式(5)和式(6)计算得出,仿真模型的交错角α范围为-2°~2°,排量角β为一个固定角度15°,将交错角α和排量角β的值代入到式(5)、式(6)中,得出不同交错角下的有效排量角δ、错配角ε,将α、β代入到式(17)中得到单柱塞腔在过渡区的压缩体积。
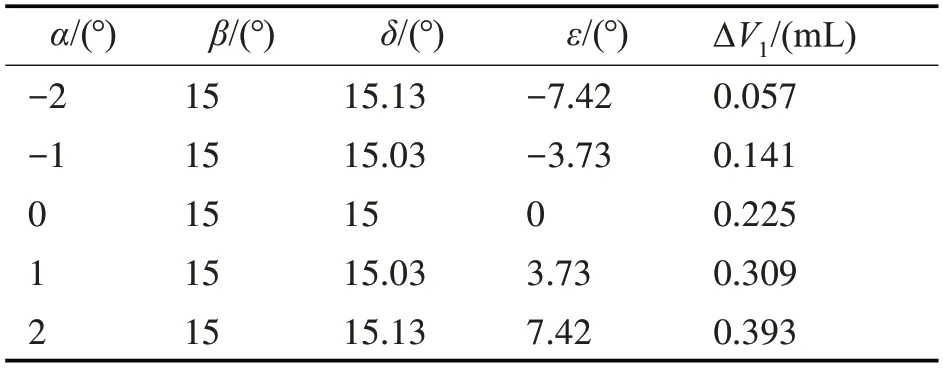
表2 交错角与过渡区压缩体积的关系
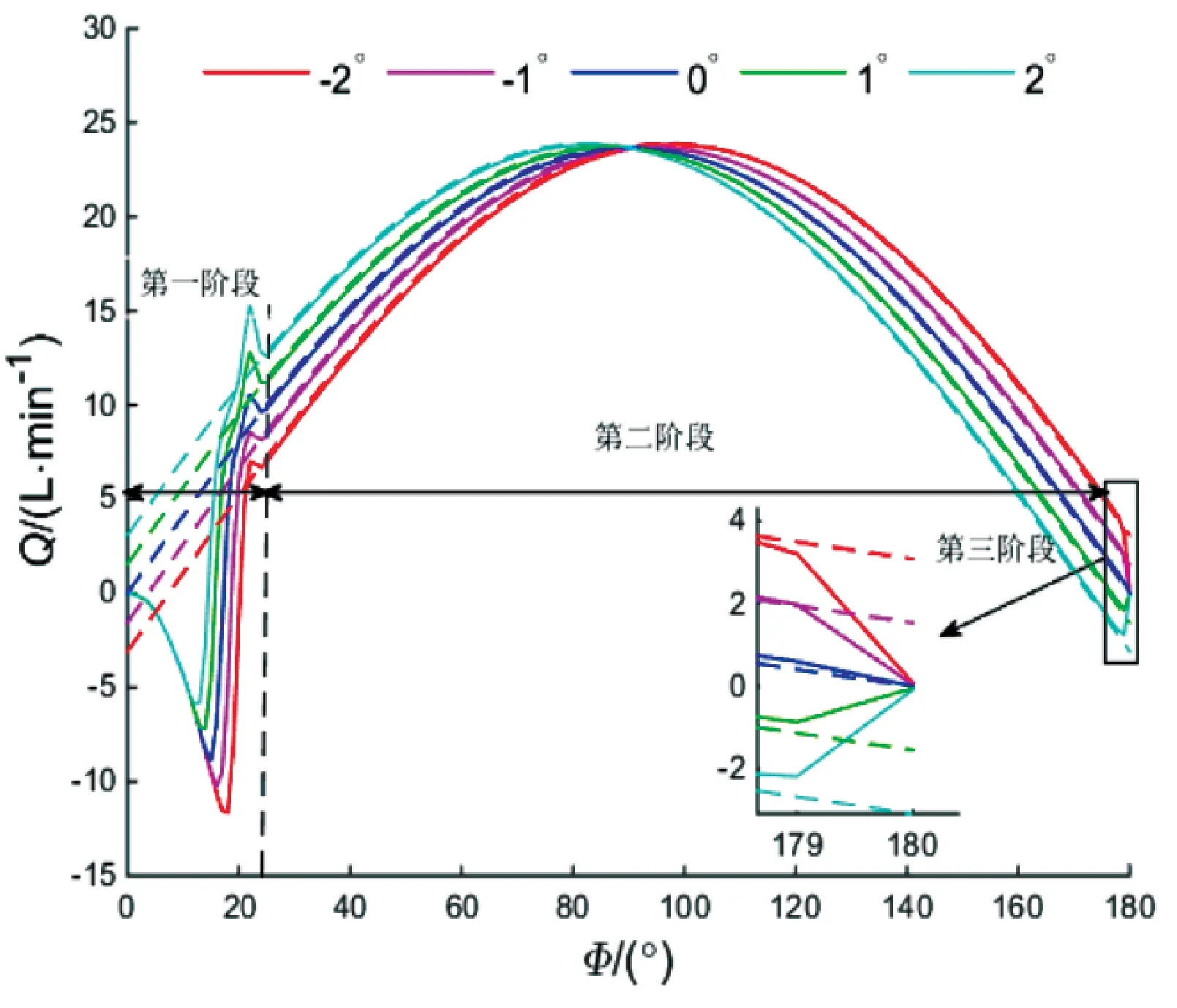
图10 不同交错角下单柱塞腔的几何流量与仿真流量
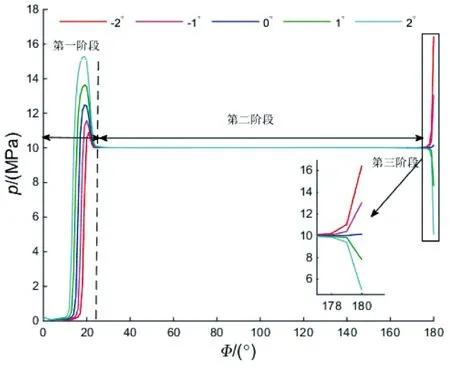
图11 不同交错角下单柱塞腔内的压力变化
图10中的横坐标Φ表示柱塞腔转动的角度,虚线是根据表2中的δ和ε代入式(18)计算得出的几何流量曲线,实线是通过PumpLinx仿真软件计算得出的仿真流量曲线。
在第一阶段,柱塞腔中的流体不仅受到倒灌流量的压缩,也受到柱塞运动的压缩,从表2中可以看出斜盘交错角越大,柱塞在三角槽过渡区的压缩体积越大,较大的压缩体积有助于抑制流量倒灌现象,从而减小流量曲线的凹陷。此外,由于流体的惯性作用,柱塞腔中的流体被过度压缩,又从柱塞腔反弹流回出口腰形槽中,形成一个波峰,从图10中可以看出,斜盘的交错角越大,波峰的幅值越大。
在第二阶段,柱塞腔内的流体充分压缩后不再反弹,在这一阶段内,仿真流量与几何流量重合,柱塞泵的流量脉动完全由几何流量决定。
在第三阶段,柱塞腔运动到与排油腰形槽的末端部分重合,两者之间的流通面积急剧减小,流通阻尼极大,造成柱塞腔内近似处于封闭状态。如果斜盘的交错角为正,柱塞的负向速度会导致柱塞腔内的液体膨胀;如果斜盘的交错角为负,柱塞的正向速度会导致柱塞腔内的液体被压缩。
图11是单柱塞腔仿真过程中的压力变化情况,当柱塞处于第一阶段,柱塞运动的压缩作用和倒灌流量导致柱塞腔内的压强急剧升高,造成压力超调。从图11中可以看出,斜盘交错角越大,柱塞腔内的压力超调量也越大,说明增大交错角虽然能减小流量倒灌,但会增加压力超调量。第二阶段柱塞腔内的压力平稳,几乎没有变化。第三阶段,正的斜盘交错角导致柱塞腔内的流体膨胀,负的斜盘交错角导致柱塞腔内的流体压缩。因此,正的交错角可以让柱塞腔内的压力减小,有助于减小柱塞腔与入口的压差。
6 整泵的工况分析
整泵的仿真模型如图12所示,本文采用的是7柱塞泵,除柱塞数目外,整泵的仿真模型参数与单柱塞腔的仿真模型完全相同,本文将考察柱塞泵在不同转速、压力下的流量脉动率。
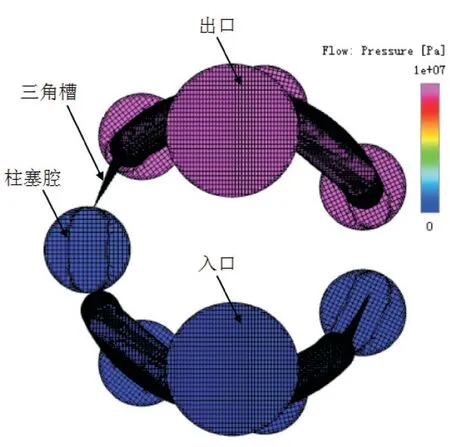
图12 整泵的仿真模型
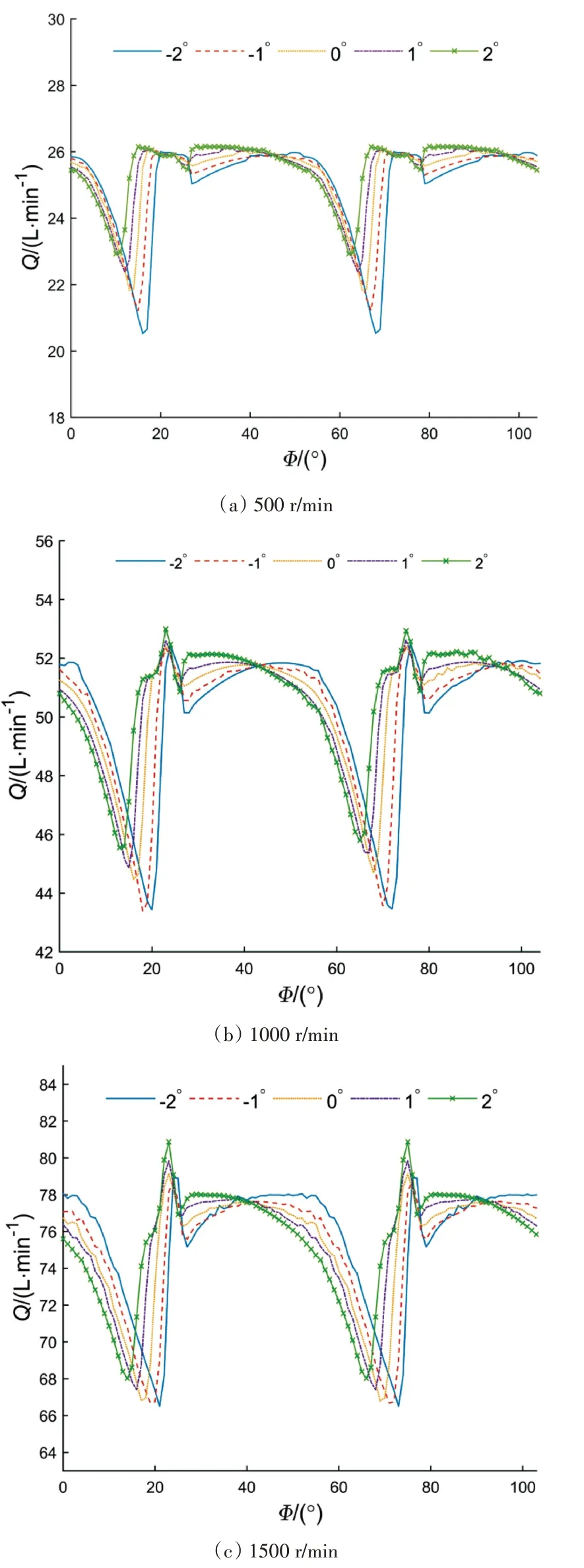
图13 不同转速下的出口流量
柱塞泵流量脉动率的计算公式[15]如下:
式中η表示流量脉动率,Qmax为波峰的平均值,Qmin为波谷的平均值。
根据图13中的出口流量和式(19)得到不同转速下的流量脉动率(表3)。从表3中可以看出,500r/min~1500r/min范围内的脉动率均值随着交错角的增加而减小,当交错角为2°时,脉动率均值最小。
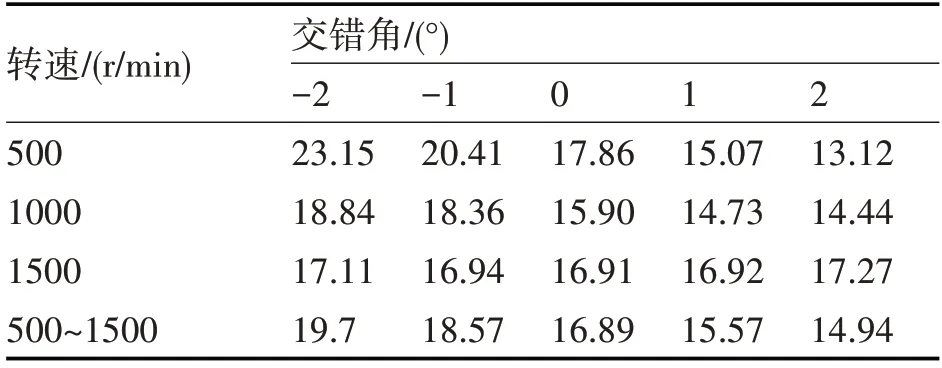
表3 不同转速下的流量脉动率(%)
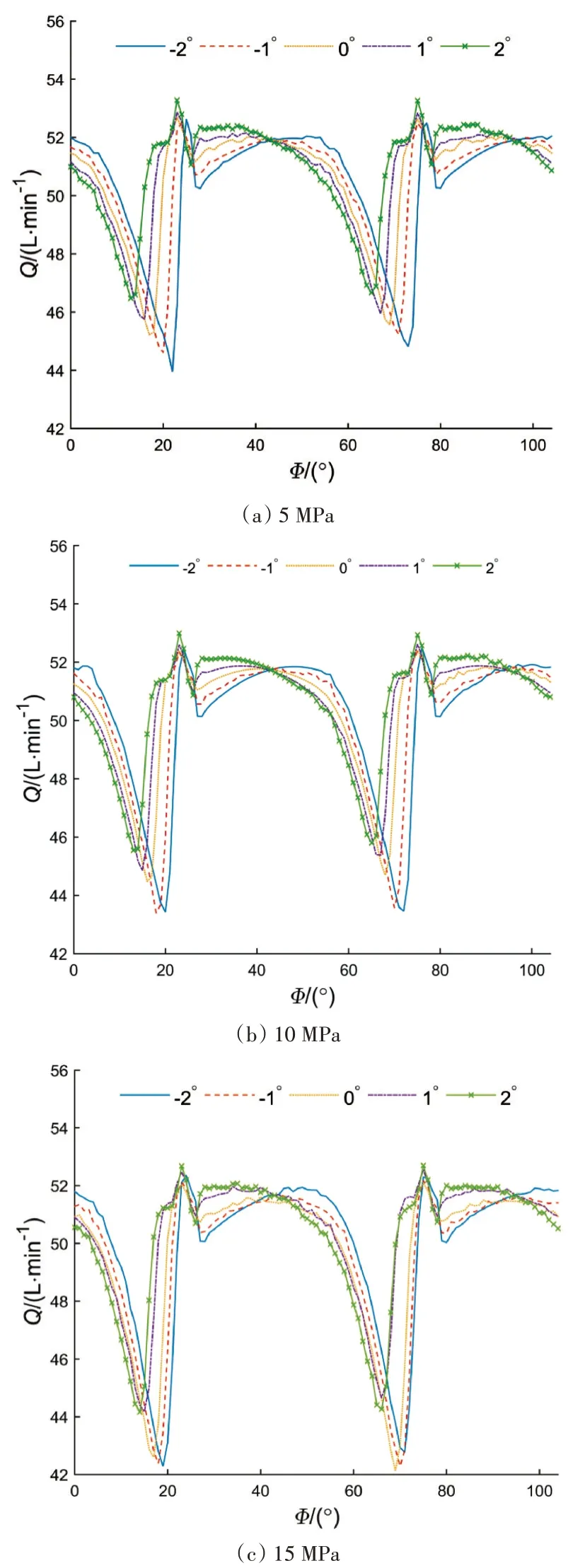
图14 不同压力下的出口流量
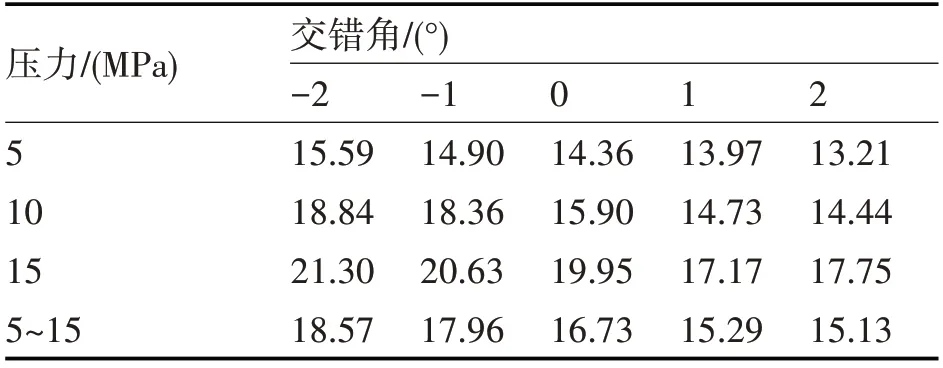
表4 不同压力下的流量脉动率(%)
根据图14中的出口流量和式(19)得到不同压力下的流量脉动率(表4)。从表4中可以看出,5MPa~15MPa范围内脉动率均值随着交错角的增加而减小,当交错角为2°时,脉动率均值最小。
虽然无论是转速还是压力的脉动率均值都是交错角为2°时最小,但都与交错角为1°的脉动均值相差不大。如图11所示,考虑到当交错角为2°时,柱塞腔内的压力超调量较大,所以取斜盘角错角为1°是较为合适的设计。
7 结语
本文通过数学分析建立了交错角与柱塞压缩体积的函数关系。使用PumpLinx软件仿真不同交错角下单柱塞腔的压力流量情况,和不同工况下的柱塞泵的出口流量,总结得出以下结论:
1)交错角对三角槽过渡区的压缩体积有重要影响,交错角每增加1°,过渡区压缩体积增加0.084mL。
2)增加交错角可以减小单柱塞腔的倒灌流量,但会增加柱塞腔内的压力。
3)综合考虑柱塞泵的流量脉动率和压力超调量,取柱塞泵的斜盘交错角为1°是较为合适的设计。
