机床丝杠进给系统热误差测点优化及实验

袁 江，陶 涛，许 凯，任 东

（1.南通大学机械学院，江苏 南通 226019；2.南通国盛智能科技有限公司，江苏 南通 226000）

1 引言

随着工业发展的需求，对零件的精密性提出了更高的要求，而热误差是影响机床加工精度的主要因素，对热误差进行补偿是提高加工精度的有效手段[1-2]。由于机床丝杠进给系统温度场分布较广，测点选择较少则不能准确的体现出温度的变化规律，如果选择较多，不仅监测成本提高，不同测点间的复共线性关系严重影响着建模精度，因此温度测点的选择是数控机床热误差补偿技术中的关键问题。

近年来，热误差测点优化问题得到了广泛研究，如改进系统聚类法[3]、偏相关分析法[4-5]、特征提取法[6]、逐步线性回归法[7]、模糊聚类[8-9]等。改进系统聚类法采用单一的相关性分析法计算热误差的相关性，会导致输入量之间的共线性；偏相关分析法可准确获取温度与热误差之间的线性相关性，但选择关键测点数量会随着测点的增多而增多；逐步线性回归法对每个温度变量进行F检验，消除了自变量之间的多重共线性；模糊聚类不能很好的确定阈值λ，阈值不同，对应的测点优化结果也不同。

提出一种综合热误差测点优化方法。首先采用Pearson 相关系数法，将温度与热延伸量数据相关性较小的点剔除；然后采用灰色关联系数法对剩余温度变量相关性进行分析，构建模糊相似矩阵；再由模糊聚类算法得出模糊等价矩阵后利用F统计量确定最佳λ 阈值；最后采用偏相关性分析法，剔除掉相关性较弱的测点后得到最佳测点组合。该方法不仅减少了测点数量，降低温度变量之间的耦合度，同时降低了热误差的复共线性，提高了建模精度。

2 综合测点优化

测点优化算法综合利用了相关分析法、灰色关联法、模糊聚类算法、F分布检验法和偏相关分析法。具体步骤如下：

2.1 Pearson 相关系数法

采用相关系数法可以表示出温度数据与热延伸量之间的关系，设X=｛x1，x2，…，xp｝为p个温度变量的集合，其中xi=［xi1，x i2，…，xin］，（i=1，2，…，p）为第i个温度变量的第n个观测值，同理Y表示不同时刻热延伸量的集合，相关系数表示为：

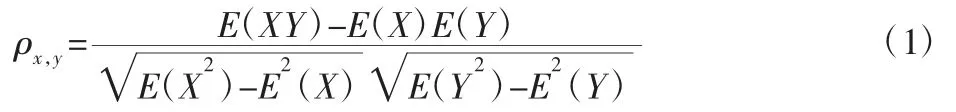
2.2 灰色关联分析法

筛选出相关性较高的点后采用灰色关联分析法，通过对象间发展趋势的相似度，来衡量温度变量间关联程度。由于在实际生产加工中环境复杂，除刀具自身振动外容易受到其他因素的影响，灰色系统理论以其处理含有系统贫乏信息的小样本序列和受噪声干扰的数据的优点，可将其灰关联度用来描述温度变量间的关联度，再通过一定的方法建立热误差与温度变量之间的关系。灰色关联分析法评价模型建立步骤如下：

（1）数据规范化处理。灰色关联度需要在等权空间中对数据进行处理，温度变量虽然量纲相同，但不同测点间以及相同测点在不同时间段中的数值差异较大，为了便于比较，应对数据进行标准化处理，这里采用的是极差变换法对原始数据进行处理，即：

（2）灰色关联系数。经规范会数据处理后温度序列集合为X′其中，p—温度传感器个数；n—第i个温度变量的第n个观测值。设x0为在集合X′中任选一行的参考序列，集合X′中其他所有行为比较序列。则x0与在第k个数据的灰色关联系数为：

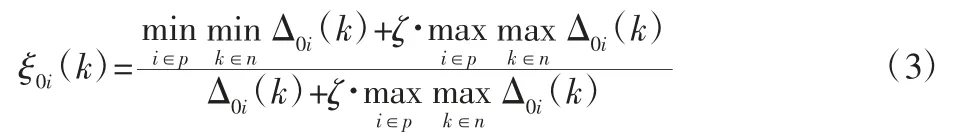
（3）灰色关联度。该序列与对应序列之间灰关联系数的平均值，即：

根据式（3）可计算出所有温度变量间的灰色关联度，可构建灰色关联度矩阵R=（rij）p×p。

2.3 模糊聚类分析

模糊聚类中的模糊关系是根据各温度变量之间的相关性所建立，再利用模糊关系对温度变量进行聚类。将灰色关联度矩阵作为初始模糊矩阵，用模糊矩阵进行模糊聚类分析。

2.3.1 模糊相似矩阵

采用灰色关联法求得灰色关联系数构建模糊相似矩阵R=（rij）p×p，设X=｛x1，x2，…，xp｝为p个温度变量的集合，其中xi=［xi1，xi2，…，xin］，（i=1，2，…，p）为第i个温度变量的第n个监测值。

2.3.2 模糊等价矩阵

模糊相似矩阵不具有传递性，因此须将相似矩阵转化为模糊等价矩阵，满足自反性、对称性、传递性3 个条件才能进行合理的分类。对模糊相似矩阵进行自平方求得R的传递闭包t（R），经过有限次的自平方后存在k使得R2k=R2（k+1），此时模糊等价矩阵即为t（R）=R2k。

2.4 F 分布统计

从模糊等价矩阵中可以提取不同的λ 值，每一个λ 对应着不同的分类，由方差理论可知通过F分布检验可以得知类与类之间差异是否显著，分类是否合理。

3 实验验证

3.1 实验数据采集

以某高速龙门加工中心为实验平台，利用无线传感标签技术实时监测各测点位置的温度变化情况，同时利用激光位移传感器监测丝杠的热延伸量，监测系统，如图1 所示。

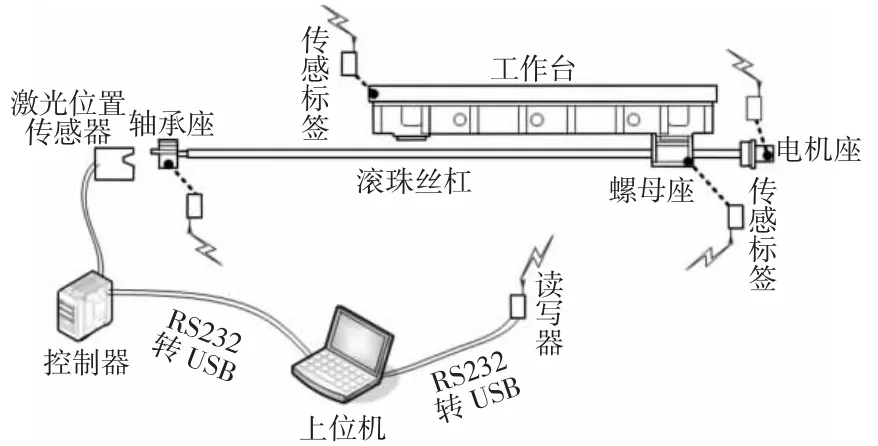
图1 实验监测系统图Fig.1 Experimental Monitoring System Diagram

由于丝杠进给系统热源分布较广，需要在不同部位安装传感标签，传感标签的安装位置，如表1 所示。其在机床中的布局，如图2 所示。

表1 传感标签安装位置Tab.1 Sensor Label Installation Location

图2 传感标签现场布置图Fig.2 Site Layout of Sensor Labels

实验时机床的运行状态为空转连续运行，进给速度为6m/min，运行一段时间后在激光位移传感器测量范围内停止一小段时间间隔，以便测量丝杠的轴向热延伸量，激光位移传感器的安装，如图3 所示。

图3 激光位移传感器安装位置Fig.3 Installation Position of Laser Displacement Sensor

3.2 温度测点优化

将各测点数据带入式（2）进行规范化处理，以减小相同量纲下数据之间差异较大的问题。以某一列温度值作为比较序列，在求出两级极大值与极小值后根据式（3）可得出每个比较序列的灰色关联系数，对每个参考序列下的灰色关联系数取平均即为灰色关联度，由此构建模糊相似矩阵R。根据模糊聚类分析原理，求出模糊等价矩阵后即可根据不同的λ 值对各测点进行分类，计算结果，如表2 所示。由表2 可以看出，当λ 值为0.802 时，F与F0.05差值较大，表明类与类之间的差异显著，分类较合理。当λ=0.802时，温度变量被分为3 类，如表3 所示。

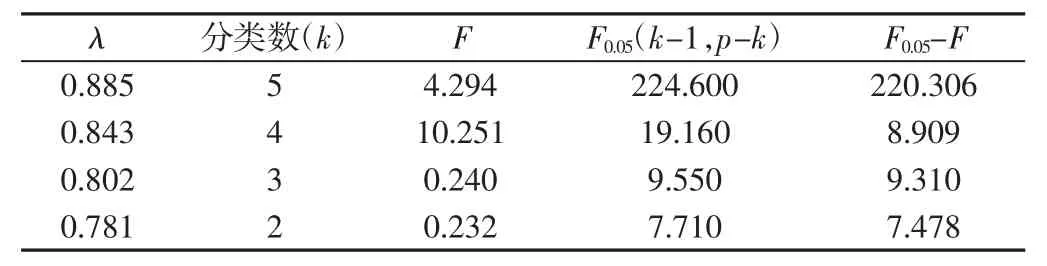
表2 阈值λ 及F 统计量值Tab.2 Threshold Value of Lambda and F Statistics

表 3 λ=0.802 分类情况Tab.3 Classification of Lambda λ=0.802

从表3 可以看出，第1 类中的温度变量较多，如果将其全部选中可能会由于和第2 类、第3 类的点产生复共线性，对建模精度造成较大影响，由（3）式算得T1 与T2 以及T5 与T4 之间的灰色系数较大，因此将T1 与T5 剔除。对应温度变量间的关系，将关系较大的变量剔除。采用偏相关性分析法，控制一个变量对另一个变量与热延伸量的相关性进行分析，结果显示T11 在控制T7 变量后与热延伸量的相关性比T7 控制T11 变量后与热延伸量的相关性较大，说明T7 对热延伸量的影响比T11 要小，因此将T7 剔除可较小复共线性，提高建模精度。综上所述，经过综合测点优化后，所选测点为T2、T4、T11。

3.3 结果分析

利用最小二乘法多元线性回归模型对所选温度变量建模。经过综合测点优化算法得到关键测温点后建立模型结果为：

△z=0.0036△T2+0.0008△T4+0.0016△T11-0.1261

式中：△z—丝杠的热延伸量；△T2、△T4、△T11—优化后各温度测点的温升。

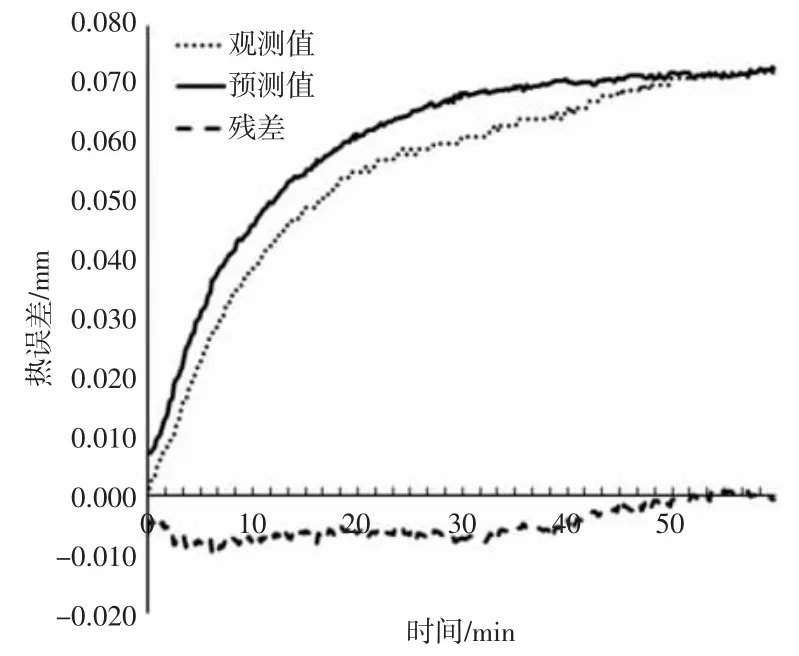
图4 综合测点优化热误差模型预测图Fig.4 Optimization of Thermal Error Model Prediction with Comprehensive Measuring Points

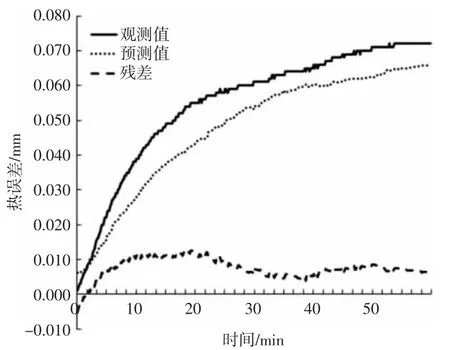
图5 灰色关联模糊聚类热误差模型预测图Fig.5 Grey Relational Fuzzy Clustering Thermal Error Model Prediction Chart

该模型的热误差预测曲线，如图4 所示。采用单一灰色关联分析及模糊聚类算法得到的热误差预测曲线，如图5 所示。图中的残差值为实测值与模型预测值之间的误差，可以有效比较出模型的预测精度。从图4 可以看出，采用综合测点优化方法，去除复共线性影响的测点后所建立模型的残差为10μm，而如图5 采用简单的灰色关联与模糊聚类所建立模型的残差为13μm。可见采用消除复共线性的综合测点优化算法建立的模型精度更高，预测效果更好。

4 结论

（1）采用综合测点优化算法，对丝杠进给系统热误差进行了预测，并在某龙门加工中心进行实验验证，结果显示温度测点由12 个减小到 3 个，丝杠热延伸量从 13μm 减小到 10μm；（2）采用F统计量对阈值λ 进行了筛选，确定了最优分组，为热误差建模奠定基础；（3）采用偏相关分析法，消除了复共线性，避免某温度变量与热误差的相关性受其它温度变量的影响，提高了热误差模型的预测精度。