基坑开挖引起下卧地铁隧道变形的简化计算方法
2021-04-02邱居涛欧孝夺龙团元侯凯文赖增任
江 杰,邱居涛,欧孝夺,龙团元,侯凯文,赖增任
(1.广西大学 土木建筑工程学院, 广西 南宁 530004;2.广西大学 工程防灾与结构安全教育部重点实验室,广西 南宁 530004;3.广西大学 广西防灾减灾与工程安全重点实验室,广西 南宁 530004)
近年来,随着城市地铁建设的大规模发展,在既有地铁线路上方建造的商业建筑也随之增多。基坑施工通常先于主体结构施工,基坑开挖难免会对周围土体产生扰动,导致下卧隧道纵向不均匀变形、地下水渗漏、轨道脱离等。因此,确保地铁隧道结构稳定和运营安全尤为重要。
为了研究下卧隧道在基坑开挖卸荷下的变形响应,在试验研究方面,张玉伟等[1]、姚爱军等[2]利用模型试验研究了上方基坑开挖卸荷-加载作用下地铁盾构隧道的变形特征及围土压力分布规律。对于计算分析方法而言通常有两种,第一种是数值模拟,Dolezalova[3]、Xiao等[4]、Huang等[5]和郑刚等[6]使用FEM模型分析基坑开挖引起的隧道变形规律,并针对不同的影响因素进行了模拟。但该方法建模复杂且计算耗时。第二种为两阶段分析法,第一阶段根据解析解得到基坑开挖卸荷引起的土体附加应力,第二阶段假设基于弹性均质地基模型计算由于附加应力导致的隧道变形,相关学者对此已经进行了大量的研究[7-12]。但既有研究均假定施工场地为均质土体,而在实际施工过程中,不同土体之间差异性较大,土体的成层性不可忽略。此外,土体并非由一系列独立弹簧所组成,在外荷载作用下,土层相互之间存在剪切变形,以往研究将隧道搁置于Winkler地基模型中,仅考虑地基基床系数对隧道变形的影响是存在缺陷的。因此,提出一种不但能体现土体分层特性,而且能反映土体单元之间剪切作用的简化计算方法更具现实意义。
本文基于弹性层状体系基本解,提出了考虑分层效应的基坑开挖扰动地层附加应力的计算方法,改变了过去研究该问题时考虑均质地基的单一现状。首先以弹性层状体系应力解取代传统的Mindlin应力解[13]计算开挖卸荷土体扰动作用于隧道的附加应力,通过引入剪切参数求解出Winkler-Pasternak地基模型中下卧隧道的纵向变形响应。最后将有限元数值模拟与工程监测数据进行对比,证明本文所提出简化方法的正确性。
1 两阶段分析法
1.1 弹性层状体系应力与位移基本解
n层土体构成的弹性地基模型受轴对称垂直荷载的作用简图见图1。图1中,p(r)为轴对称荷载;δ为荷载半径;Δhi(i=1,2,…,n)为第i层体系厚度;Ei、μi分别为第i层体系的弹性模量和泊松比。

图1 轴对称荷载施加于多层地基表面示意图
参照Burmister弹性层状理论解[14-16],推导多层弹性体系中任意深度z处的应力和位移解表达式
(1)
(2)
(3)
(4)
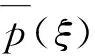
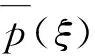
(5)
矩阵L和K定义为
(6)
式中:z为计算点深度;hi为第i层土体底部到地表面的距离,Φ(ξ,z)称为传递矩阵,定义为
(7)
传递矩阵Φ各元素表达式为
(8)
式中:E和μ为对应于层状体系中每一层土的弹性模量和泊松比。
1.1.1 表面受集中荷载作用的解析解
当多层地基表面作用一集中荷载p时,p(r)的表达式为
(9)
式中:δ(r)为Dirac函数,定义为
(10)
结合式(5)、式(9)和式(10),可以得到p(r)经过Hankel积分变换后的表达式为
(11)
将式(11)代入式(2)和式(4)中,可得集中荷载作用下,与集中荷载水平距离为r处的地基表面的位移和地基内任意深度z的竖向附加应力,表达式为
(12)
(13)
1.1.2 表面受矩形均布荷载作用的解析解
设基坑的长度和宽度分别为a和b,作用在坑底的垂直均布荷载为p0,见图2。
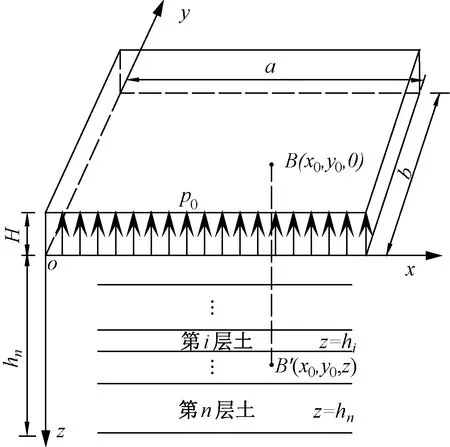
图2 层状地基矩形荷载分布
(14)
p0可按下式计算
(15)
式中:γi、hi对应于第i层土底部以上土层的单位重度和厚度。
利用式(12)、式(13)对矩形面积积分,可得到矩形均布垂直荷载作用下,荷载作用面任意点B(x0,y0,0)处的位移和荷载作用面以下任意点B'(x0,y0,z)的竖向附加应力表达式
(16)
(17)
式中:Ω为矩形均布垂直荷载的面积。
1.2 隧道在开挖卸荷作用下的变形分析
基坑与盾构隧道相互作用的简化模型见图3,将盾构隧道简化成Euler-Bernoulli长梁,假定隧道与周围土体完全接触并且土层为各向同性的弹性体,地基土体的非线性变化不纳入计算考虑范围。Winkler和Winkler-Pasternak地基模型的隧道变形的平衡微分方程表达式为
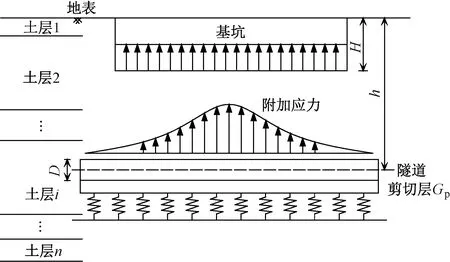
图3 盾构隧道受基坑开挖影响示意图
(18)
式中:EI为盾构隧道的抗弯刚度;k为地基基床系数;Gp为土体的剪切模量;δ(x)为隧道的挠度;D为盾构隧道的外径。
因微分方程中存在四阶导数,根据有限差分定理Δmfk=hmf(m)(ξ)可对导数进行降阶,表达式为
(19)
将隧道划分为n+5个节点,每个节点长为l,所受附加应力为σz(i),竖向位移为δi,将式(19)代入式(18)并整理成矩阵形式为
(20)
式中:Q为作用于隧道的附加应力并可由式(17)获得;δ为隧道的纵向位移;ψ1、ψ2、ψ3为系数矩阵。
假设隧道足够长且10倍基坑开挖尺寸之外隧道两端剪力和弯矩为零[18],由此可知边界条件表达式为
(21)
根据上述边界条件,进一步推导出系数矩阵ψ1、ψ2、ψ3的表达式为
(22)
(23)
ψ2为(n+1)×(n+1)阶单位矩阵。
将ψ1、ψ2、ψ3的表达式代入式(20)并用Matlab进行编程求解,便可得到Winkler和Winkler-Pasternak地基模型下隧道的隆起值δ,分别对δ进行二阶、三阶求导便能求出隧道的弯矩M与剪力Fs,公式为
(24)
选取合适的基床系数k与剪切模量Gp是进行合理计算的前提。根据Klar等[19]的建议,本文计算采用2倍Vesic基床系数值
(25)
式中:Es为隧道所处土层弹性模量。
对于剪切模量Gp的取值,通常采用简化弹性空间法[20],即
(26)
式中:Gs为土层的剪切模量;Hp为剪切层的厚度并取[21]Hp=2.5D。
2 算例验证
2.1 与均质地基中附加应力的对比
某基坑开挖平面尺寸为32 m×16 m,开挖深度为8 m,场地共有四层土,具体参数见表1。

表1 施工场地土体参数
为分析地基土体的非均质性对基坑开挖扰动地层附加应力的影响,选取基坑底面中心以下15 m处平行于基坑短边的纵向不同节点,将均质地基与分层地基两种情况土体竖向附加应力进行了对比,其中,均质地基的土体模量按Poulos等[22]提出的加权平均值计算,经折算后均质土体弹性模量取101 MPa,泊松比取0.26。
两种不同地基下的附加应力分布见图4,规律大体相似。两者的附加应力均在x=0处达到最大,在距基坑中心12 m外均质地基中附加应力值要大于分层地基的附加应力值,而0~12 m内分层地基附加应力值大于均质地基附加应力值。由于土体弹性模量自上而下依次增大,土质由软变硬将导致地基产生应力集中现象,相反,土质由硬变软将产生应力扩散现象。本节土体附加应力曲线分布规律体现了这一土力学结论。由于开挖卸荷具有对称性,以基坑中心为划分点,选取一侧的土体附加应力值进行比较分析,见表2。通过比较可知,两者之间最小应力偏差为2.4%,最大应力偏差可达67.2%,其中x=0处应力偏差为19.8%。目前计算外荷载作用下土体附加应力值主要采用基于均质地基的Boussinesq解和Mindlin解,当土层参数相差不大时,采用Boussinesq解和Mindlin解计算的土体附加应力可近似等同于弹性层状体系解;当土层参数相差较大时,Boussinesq解和Mindlin解的计算结果则与弹性层状体系解明显不同。因此在理论分析中,考虑地基土体弹性模量和泊松比的变化对于更准确计算土体附加应力是具有实际意义的。

图4 均质地基与分层地基附加应力对比
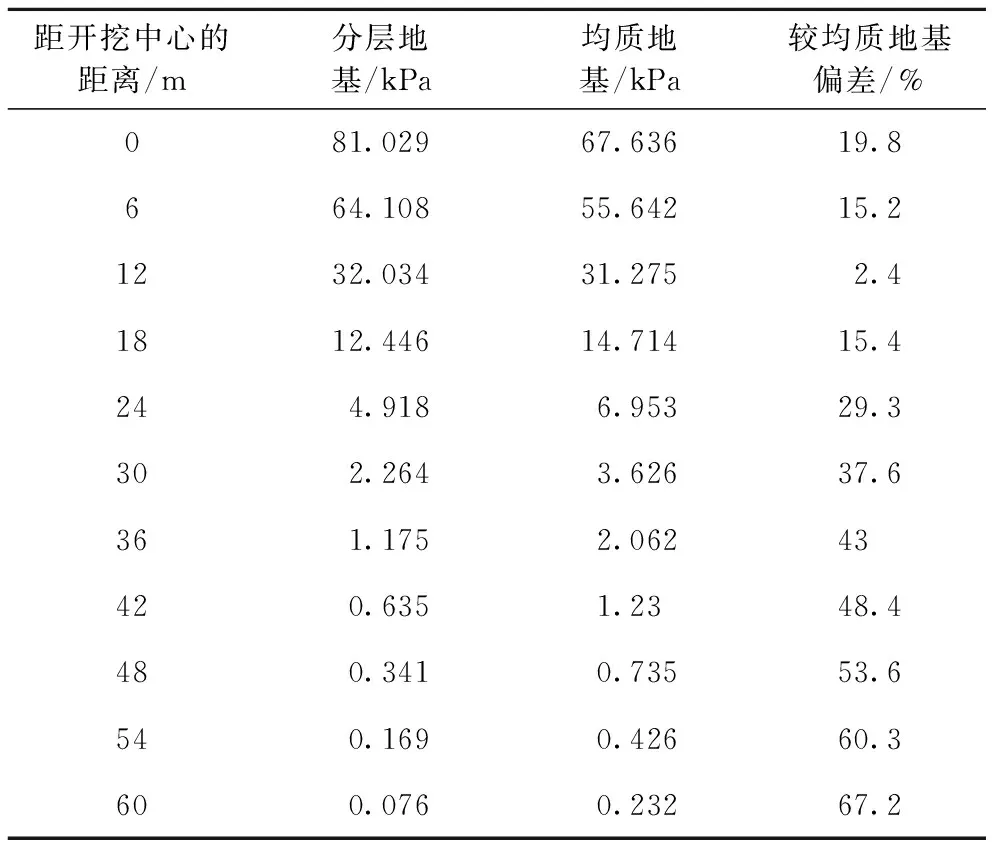
表2 不同地基模型附加应力比较
2.2 与有限元模型的对比
某基坑开挖施工恰好位于既有盾构隧道上方,基坑开挖尺寸为8 m×8 m×6 m(长×宽×深)。施工场地共有四层土,各层土体的具体参数见表3。盾构隧道位于地表以下20 m且隧道纵轴平行于与基坑长边,外径为6.2 m。隧道等效抗弯刚度(EI)eq=7.8×107kN·m2,基床系数k=4 260 kN/m3,剪切模量Gp=4.257 3×104kN/m。
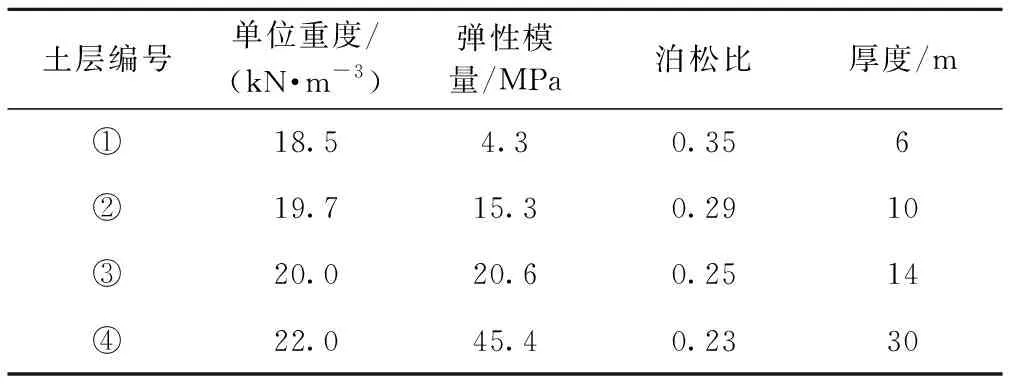
表3 模型计算参数
算例采用有限差分软件FLAC3D进行验证。考虑有限元计算中边界效应的影响,将模型尺寸定义为150 m×150 m×60 m(长×宽×高),沿着侧壁设置四道地连墙用来抵抗基坑侧壁土体的水平应力,每道地连墙厚1 m,埋深10 m。为了与理论计算中涉及的参数条件保持一致,在有限元模型中隧道采用梁单元进行模拟,周围土体采用线弹性模型进行模拟,并假设隧道与土层满足变形协调条件。有限元网格划分见图5,在整个模型区域中,网格个数共计135 218个,节点共有148 800个,以基坑中心为原点,截取位于区间x=[-75 m,75 m]的隧道进行研究。
图5 有限元网格划分示意图
采用Winkler模型、Winkler-Pasternak模型与有限元数值模拟得到的隧道隆起量对比见图6。由图6可见,三种方法中采用Winkler方法得到的数值解远大于其余两者,原因在于Winkler模型忽略了地基弹簧之间的相互作用。此外,在距离基坑中心约50 m处,隧道开始产生纵向位移。Winkler模型、解析理论得到的隧道隆起值与有限元解的对比见表4。采用解析理论计算得到的隧道纵向最大位移为2.02 mm,数值模拟为2.25 mm。在开挖影响范围内,解析理论与有限元结果的位移偏差都在40%以内,远低于Winkler模型。两种方法的计算结果分布规律基本一致,数值上存在微小差别可能原因在于基坑开挖土体扰动导致既有隧道相对刚度的减小,本文理论算法中并没有考虑这方面的影响。
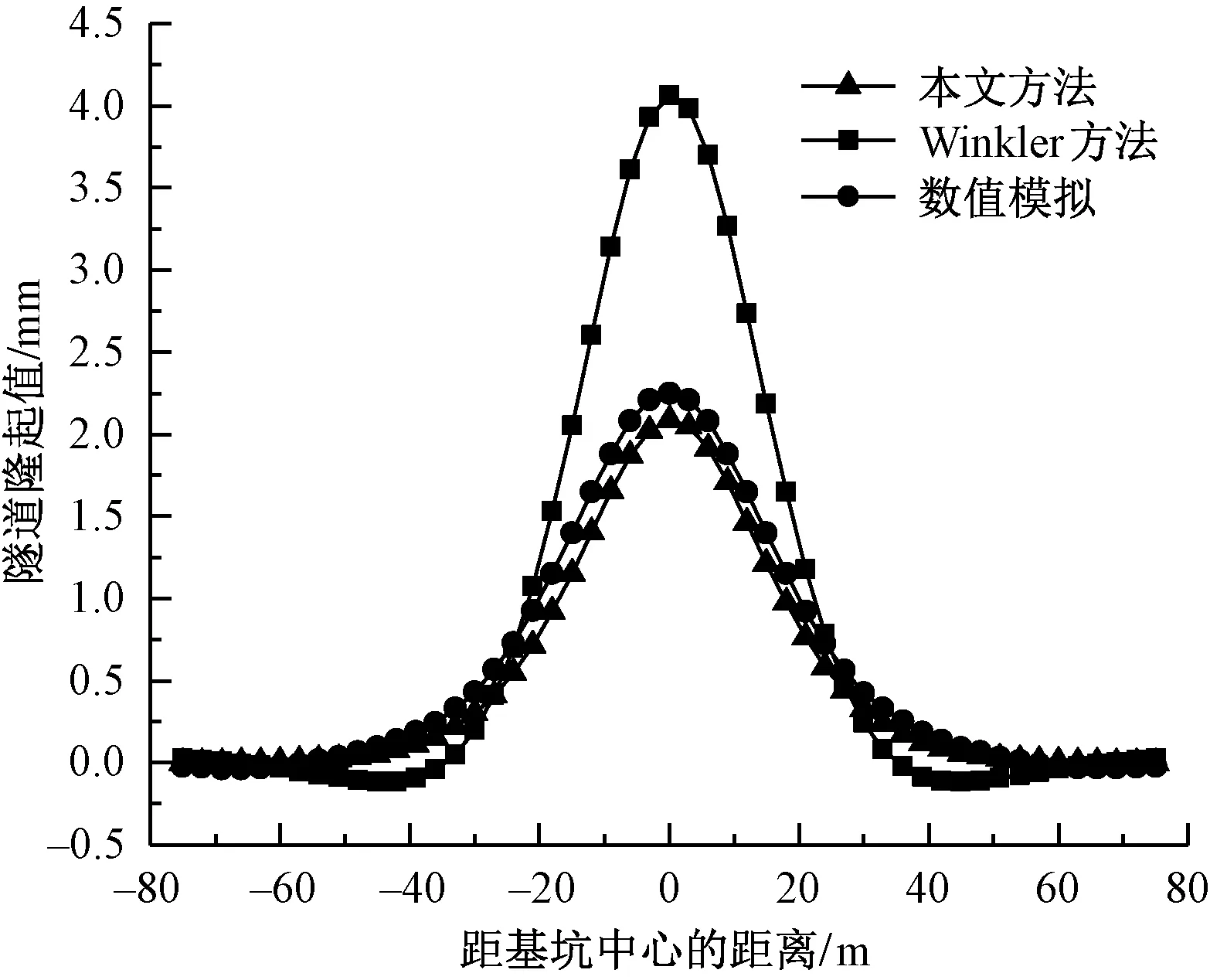
图6 隧道隆起值对比曲线
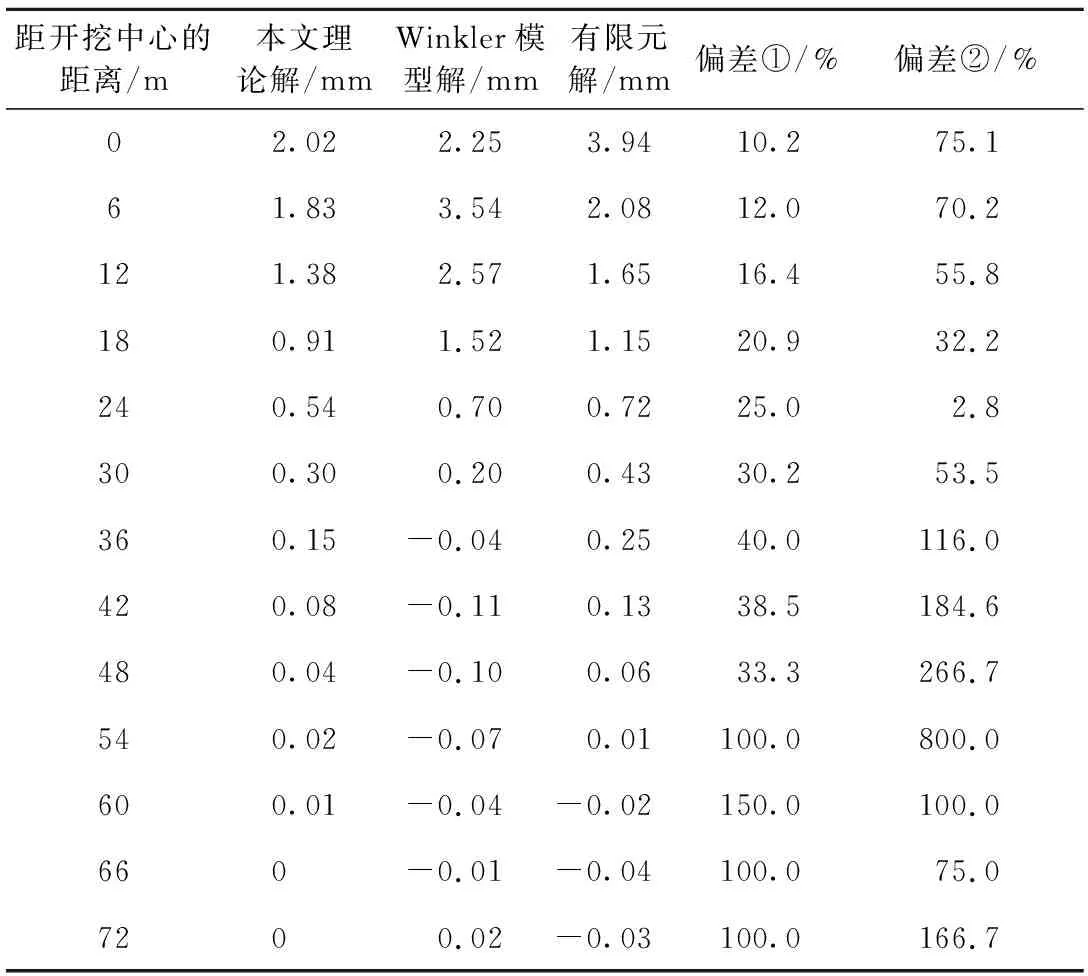
表4 Winkler模型、解析理论与有限元结果比较(隧道隆起)
隧道在附加应力作用下采用三种计算方法得到的弯矩分布图见图7。由图7可知,正弯矩最大值位于基坑中心正下方处,此时衬砌管片处于最不利受弯拉状态,最大负弯矩产生于距基坑中心两侧约25 m的位置。盾构隧道是由一系列衬砌管片拼装而成的结构体,当作用于其上的弯矩超出隧道极限抗弯能力时,衬砌管片环缝会大幅度张开从而影响隧道结构的稳定。Winkler模型、解析理论得到的隧道弯矩值与有限元解的对比见表5。采用解析理论得到的弯矩偏差均值为57.4%,小于Winkler模型得到的弯矩偏差均值148.8%,与有限元计算结果相比,Winkler模型计算得到的最大正、负弯矩值高出79.7%、105.3%,总体来说,采用本文方法与有限元算法得到的弯矩值吻合较好,曲线分布规律也基本一致。

图7 隧道弯矩对比曲线
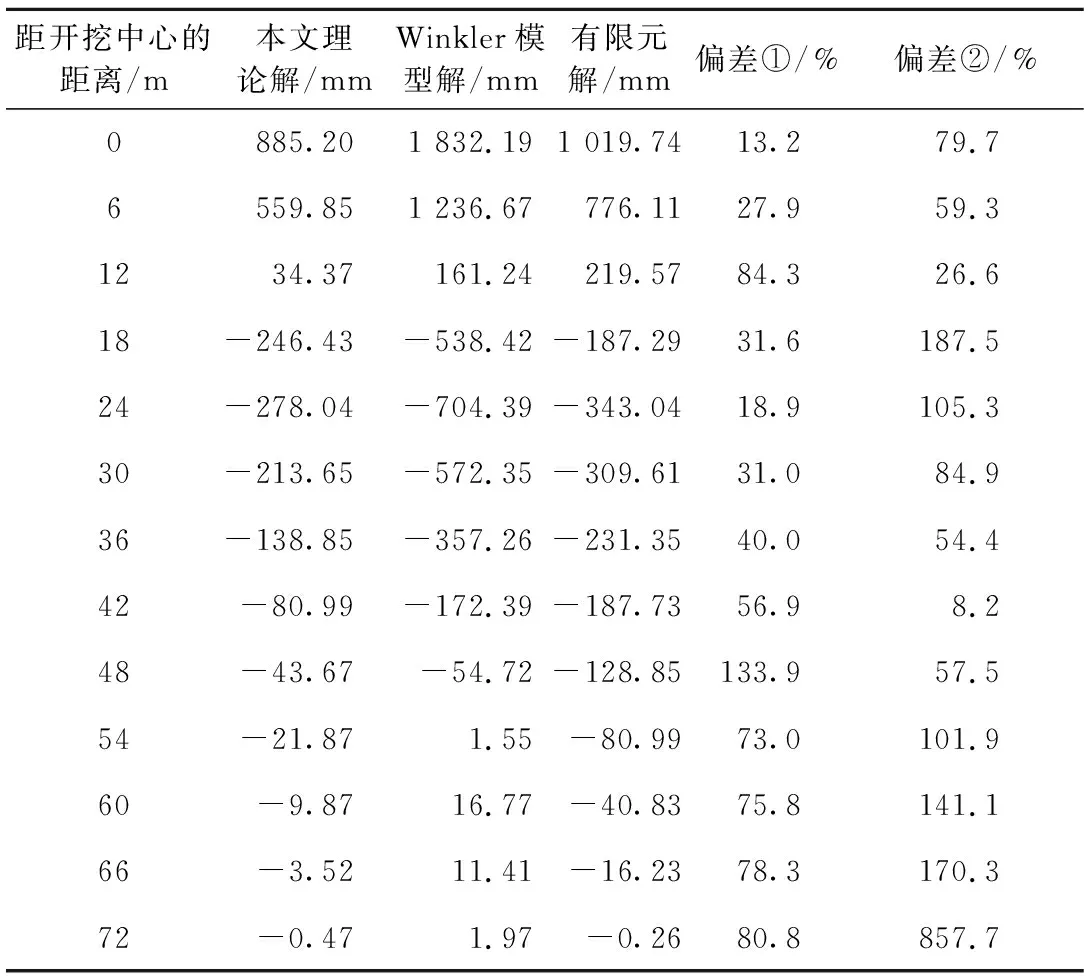
表5 Winkler模型、解析理论与有限元结果比较(隧道弯矩)
采用本文理论解、Winkler模型解以及有限元模拟得到的隧道纵向剪力对比曲线见图8。其中本文计算结果与有限元计算结果数值吻合较好,剪力最大(小)值皆发生于x=±9 m处。为了维护隧道的结构稳定,可在剪力最大处采取加固接头螺栓的办法。Winkler模型、解析理论得到的隧道剪力值与有限元解的对比见表6。在x=±9 m处Winkler模型计算出的最大(小)剪力值要超出数值模拟的82.7%。与有限元结果相比,采用解析理论得到的剪力偏差均值为62.3%,小于Winkler模型得到的剪力偏差均值108.1%。

表6 Winkler模型、解析理论与有限元结果比较(隧道剪力)

图8 隧道纵向剪力对比曲线
根据上述分析可知,在预测由于开挖卸荷引起下卧隧道变形中,本文提供了一种快速而简便的方法。
2.3 与监测数据对比
上海东方路地下过街通道采用明挖法施工,上海轨道交通2号线的一段隧道正好位于基坑正下方并与基坑成45°夹角,见图9。为了简化分析过程,将基坑视为26 m×18 m(长×宽)的矩形,各层土体参数见表7。基坑开挖深度为6.5 m且隧道顶部距离坑底仅为2.76 m,地铁隧道使用盾构法施工,采用钢螺栓连接的预制节段环作为永久衬砌,厚度为0.35 m。隧道轴线位于地表以下12.36 m,地铁2号线隧道外径为6.2 m。隧道等效抗弯刚度取1.087×108kN·m2。基坑底部浇筑1.88 m厚的混凝土底板。考虑地层改良后地基刚度的增加,理论计算中隧道所处土层弹性模量取16.01 MPa。
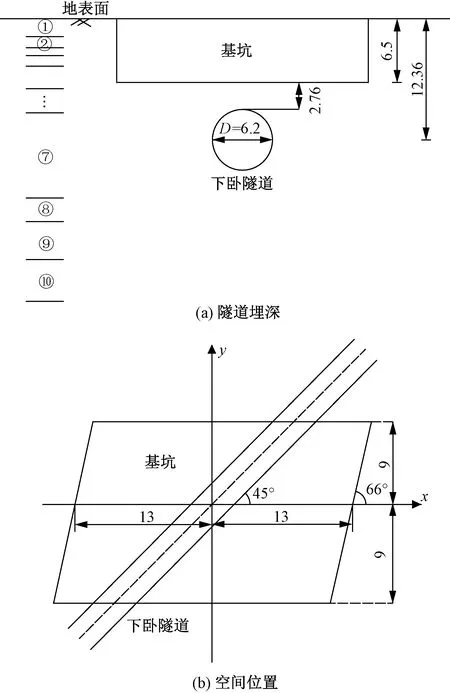
图9 基坑与隧道位置关系示意(单位:m)
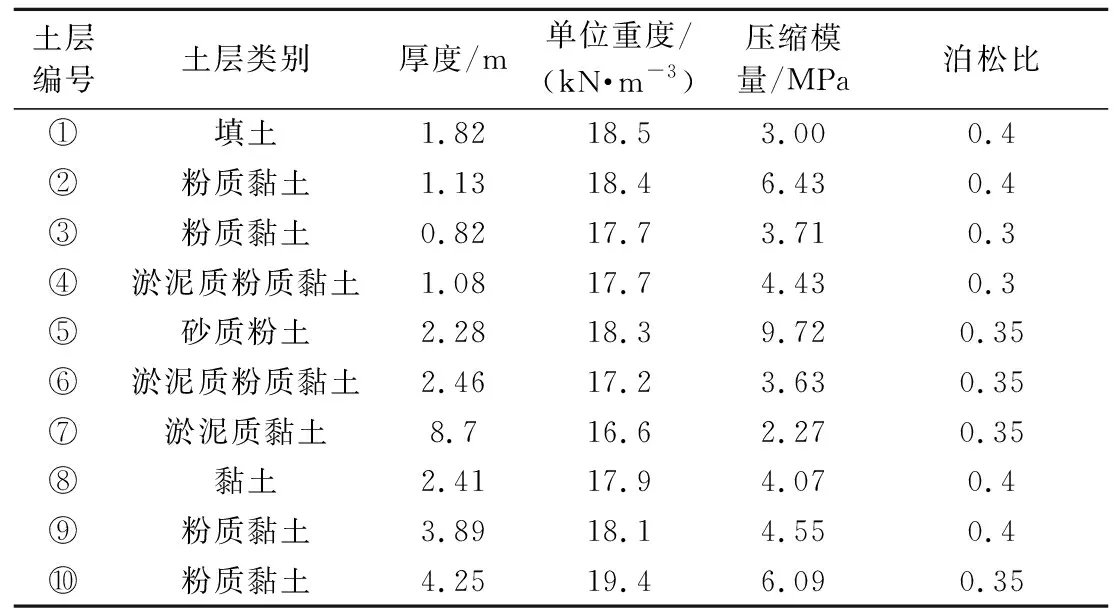
表7 场地土层参数
为了验证本文两阶段方法的适用性,将理论计算结果与现场监测结果进行了对比分析,本文理论解计算得到的隧道隆起值见图10,并与文献[23]中现场实测数据以及Winkler模型解进行了对比分析。
从图10可知,采用本文方法计算的隧道隆起值与实测数据分布规律基本一致,并且比大多数实测隆起值要大一些,原因在于实际施工过程会对基坑采取各种加固措施如分层分区开挖、底板浇筑、围护桩的打设等,然而本文理论计算没有考虑这些因素。隧道弯矩对比曲线见图11,由图10、图11可知,采用本文解析理论得到的隧道隆起和弯矩曲线低于Winkler理论模型得到的曲线,意味着如用Winkler模型进行隧道纵向变形预测,需采取过多的保护措施来减小隧道隆起量。此外,本文理论解与隧道实测隆起量都满足地铁隧道的规范标准,即隧道最大隆起值不超过20 mm。
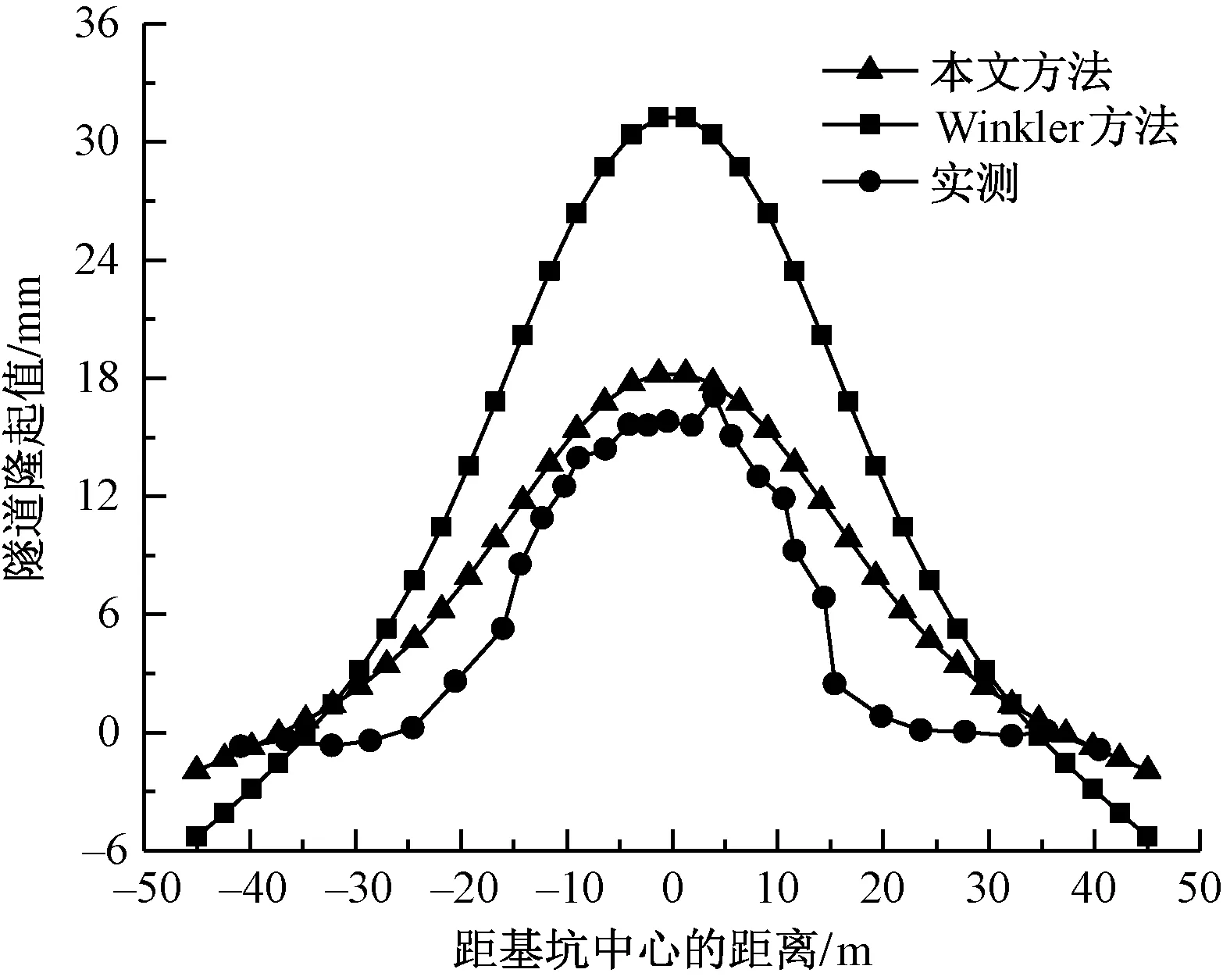
图10 隧道隆起值对比曲线
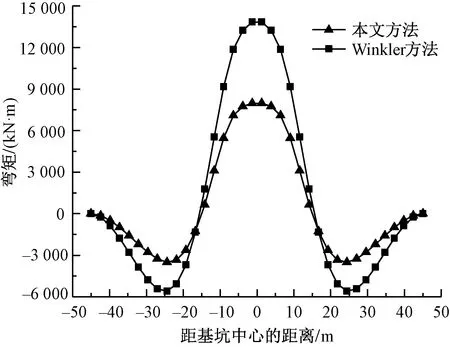
图11 隧道弯矩对比曲线
3 结论
(1)与以往基于均质地基的两阶段法不同,在计算基坑开挖卸荷作用于下卧隧道的附加荷载时,本文建立的集中荷载与矩形荷载下弹性层状体系应力解不仅考虑了弹性模量与泊松比随土体分层变化而不同的情况,还避免了均质地基中应力扩散能力过大的弊端,与工程实际情况符合,具有更好的计算精度。
(2)将地铁隧道简化为Euler-Bernoulli长梁架卧于Winkler-Pasternak地基模型中,从而建立梁的挠度平衡微分方程,通过有限差分法对方程进行降阶处理,最终得到隧道在附加应力作用下的纵向变形解答。
(3)在预测隧道纵向变形响应的方法中,采用Winkler地基模型通常导致计算结果偏大,Winkler-Pasternak模型充分考虑了土体弹簧之间的相互作用,与工程实际更贴近,计算结果更具参考性与精确性。此外,基坑中心下方区域导致隧道产生最大纵向位移且使衬砌管片处于最不利受弯拉状态,施工中应加强这部分区域的变形监测与保护力度。
(4)本文未考虑基坑侧壁土体卸荷作用以及隧道与周围土体之间的非线性作用,在将来研究中可进一步完善。
