基于列车备选集的技术站单组列车编组计划优化模型
2021-04-02魏玉光
方 波,魏玉光,杨 浩
(北京交通大学 交通运输学院, 北京 100044)
技术站列车编组计划作为货物列车编组计划的重要组成部分[1],是一个复杂的大规模组合优化问题。而单组列车作为我国技术站货物列车的主要组织形式,承担了大部分技术站间的车流运输任务。因此,技术站单组列车编组计划的优化是提高路网车流运输组织水平的关键。
大规模实际路网涉及范围广、因素多,使得单组列车编组计划成为NP-hard问题,用现有模型和方法几乎难以得到最优解,简化实际问题并求解出符合运输需要的编组计划成为研究重点。国内外学者围绕技术站单组列车编组计划开展了大量研究,研究成果主要集中于车流径路优化、单组列车编组计划优化、单组列车与分组列车编组计划协同优化、车流径路与单组列车编组计划的综合优化等方面。
车流径路优化方面:江南等[2]提出适合铁路管理方式的车流径路制定参照模型及算法,并针对各种车流径路的求解方法给出详细的数学模型与算法;温旭红等[3]以路网上车流的广义里程成本最小化为目标,以车流径路的树形结构约束、车流强度守恒以及路段通过能力限制等为约束条件,提出基于树形结构的铁路车流径路优化模型。
单组列车编组计划优化方面:史峰等[4]将给定编组去向集时有改编能力约束的编组计划问题转化为车流径路问题,提出交替添加、剔除编组去向的启发式算法;许红等[5]综合考虑车站编组能力、解体能力、调车线容车数等影响因素,构建了以技术站车流总消耗最小及改编能力利用程度最均衡的多目标0-1规划模型,并以改进的遗传算法求解;林柏梁等[6]基于最远站法则,构建了列车编组计划的双层模型,上层确定列车到发站,下层确定车流改编方案,并采用模拟退火算法对模型进行求解;Chen等[7]假设车流径路已知,构建了基于路径的单组列车编组计划线性模型,以车站最大编组去向数代替分类线数量约束来避免模型的非线性,并设计了一种启发式的树分解算法进行求解。
单组列车与分组列车编组计划协同优化方面:梁栋等[8]分析了分组列车相较于单组列车的耗费节省,在单组列车编组计划的基础上,以分组列车取代单组列车的节省最大为目标求解分组列车编组计划模型;肖杰等[9]建立了单组列车和分组列车编组计划的综合优化模型,以遗传算法求解得到的单组列车编组计划为基础,采用遍历算法求解综合优化模型;另外,Xiao等[10]开发了一种基于遗传算法和禁忌搜索的混合算法来求解单组列车编组计划模型,然后将分组列车替换为单组列车,并提出一种贪婪算法求解综合优化模型。
车流径路与单组列车综合优化方面:李德义[11]提出另一种列车备选集方法,构建以技术站车流集结、改编中转、无改编中转和走行总消耗最小的车流径路与编组计划综合优化模型,并设计基于分支定界和列生成算法的分支定价算法进行求解;林柏梁等[12]提出了将车流径路选择、装车地直达列车编组计划及技术站直达列车编组计划三者统一优化的模型;严余松等[13]根据机会约束规划理论,建立了基于车流量波动的列车编组计划与车流径路综合优化模型,并设计基于随机模拟的改进分枝定界法对模型进行求解。
文献[4-10,12-13]可归纳为“车流-车组-列车”的递归方法,即先将车流合并为车组(编组去向),再将车组分配给列车,大多基于点-弧或弧-路模型建模框架,通过引入决策变量表示车流是否在某站改编来递归求解车流的完整改编过程。这种方法容易导致模型的非线性结构,求解难度高,依赖于启发式算法,并且车流递归难以直观展示各支车流的改编过程。文献[11]可概括为“车流-列车”的研究方法,模型基于多商品网络流框架,车流改编接续过程直观,但冗余变量过多,求解结果不理想。
针对现有研究存在的不足,本文基于多商品流服务网络设计原理,提出列车备选集的方法,首先构建列车备选集,再进行车流分配,把单组列车编组计划问题转化为列车服务网络上的车流分配问题,并建立了两阶段线性规划模型分别求解最优车流径路和最优编组计划。第一阶段的车流径路模型用于求解各OD对的最优车流径路;第二阶段为编组计划模型,以上一阶段所得最优车流径路生成的列车备选集为输入,求解最优列车服务和车流分配方案。最后分别以小规模路网和大规模路网案例验证模型的可行性和结果的精确性。
1 列车备选集的构建及优化
1.1 列车备选集的构建
列车备选集是指技术站之间可开行的全部直达(直通)列车和区段列车的集合。以图1所示的直线方向5个技术站为例,t为列车,假定两相邻技术站之间必开区段列车,即t12、t23、t34、t45;方向上所有可开行的直达(或直通)列车(以下统称直达列车)为t13、t14、t15、t24、t25、t35,共6列。此时的列车备选集为{t12,t23,t34,t45,t13,t14,t15,t24,t25,t35}。同理,当直线方向有n个技术站时,备选列车数q为
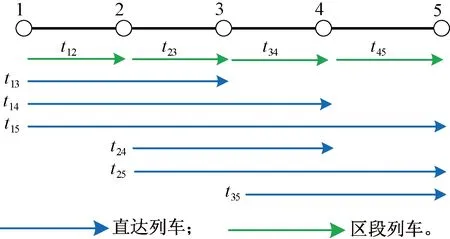
图1 直线方向5个技术站
式中:第一项为直达列车数;第二项为区段列车数。
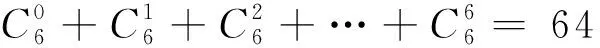
对于直线方向的铁路线路,相当于已经给定了任意两个站之间的车流径路,列车备选集的构建简单明了。简单路网示意见图2,以OD对(1,4)之间的车流为例,车流的走行径路可能为1→2→4或1→2→3→4,这两种车流径路会生成不同的备选列车{t12,t24,t124}和{t12,t23,t34,t123,t234,t1234}。因此,需要先确定路网条件下每个OD对之间的最终车流径路,从而将路网转化为各OD对间只有唯一径路的简单直线线路,以此构造路网条件下的列车备选集。
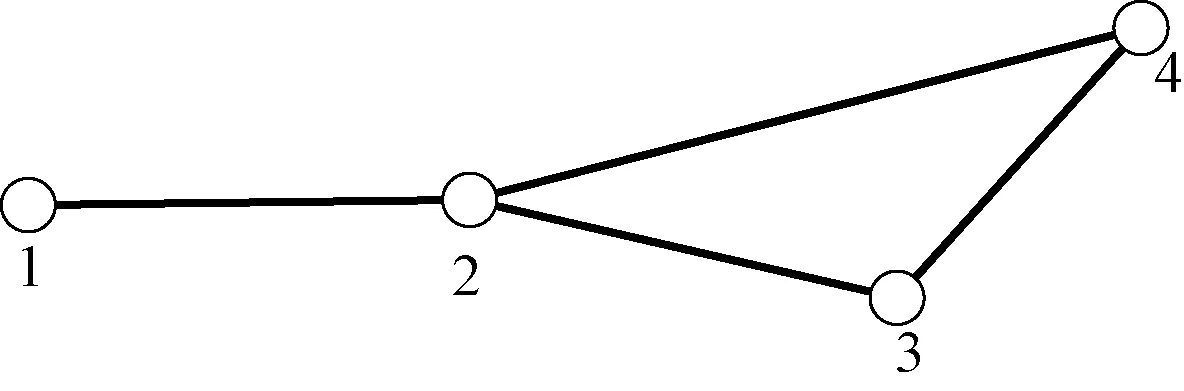
图2 简单路网示意图
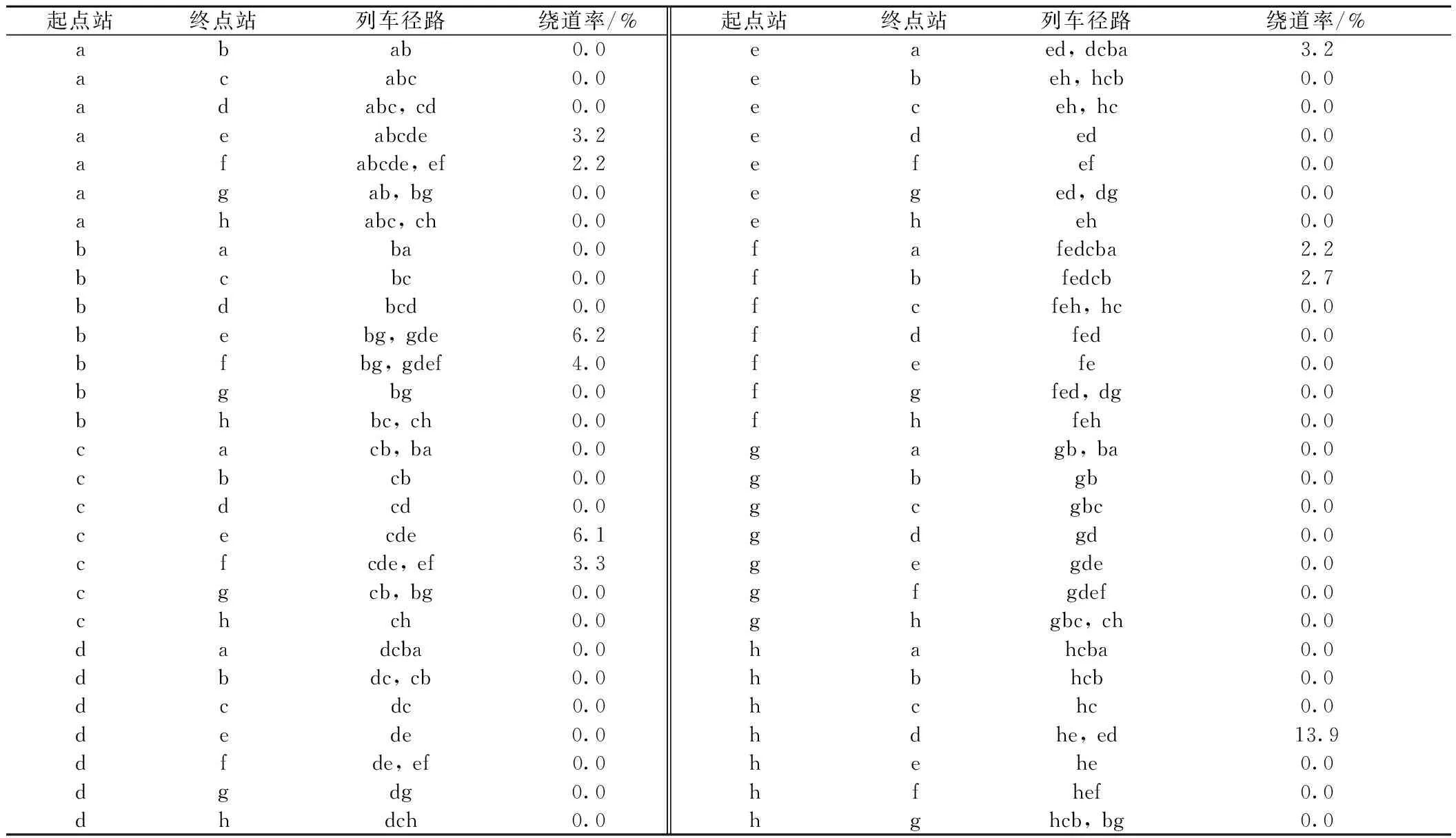
假设图2路网中所有OD间的所有车流径路都满足绕道率且最终径路已知,图2所示路网(单方向)列车备选集的构建过程见表1,剩余未列举的OD对恰好与表1中列举的对称。

表1 简单路网单方向的列车备选集构建
需要注意,对于备选集里的列车,每支车流只能选择由其车流径路产生的列车。以OD对(1,3)之间的车流为例,该支车流只能选择径路1→2→3产生的列车{t12,t23,t123}。该规定能够剔除大量冗余方案,进一步减少变量规模。
由于实际路网往往比图2所示情况复杂,每个OD对之间可能存在成百上千条车流径路,这些径路一方面难以全部纳入考虑范围,另一方面包含了大量过长的无效径路。为降低问题的复杂度,在求解各OD对间的备选车流径路时,引入车流径路绕道率μr[14]来剔除过长的不合理径路,定义为
(1)
式中:Lr为某OD间的任意一条径路r的长度;Lrmin为该OD间最短径路rmin的长度。
当某条径路的绕道率大于规定阈值(本文取1.35)时,该条径路将不予以考虑。
1.2 列车备选集的优化
上述列车备选集中的直达列车,是理论可开行的所有直达列车,而实际生产中,由于技术站作业设备、线路条件、改编时间消耗和车流量大小等条件的影响,两技术站间可能必须开行直达列车或是禁止开行直达列车,以下称为必开条件和禁开条件。
(1)必开条件
传统的分析计算法指出,若某一单支车流无改编通过其运行途中任何一个技术站所得车小时节省都大于或等于其在编成站的集结车小时消耗,则该车流满足绝对条件,可直接列入方向最优编组方案[1]。对应列车备选集,若某支车流满足绝对条件,则该车流起讫点之间必开直达列车。除此之外,规定两相邻技术站之间必开区段列车。
(2)禁开条件
编组计划需遵守技术站禁开去向规定,通过剔除禁开去向的直达列车,可以进一步缩减列车备选集。

2 单组列车编组计划两阶段优化模型
模型中的集合、参数及变量说明分别见表2~表4。

表2 集合符号及定义
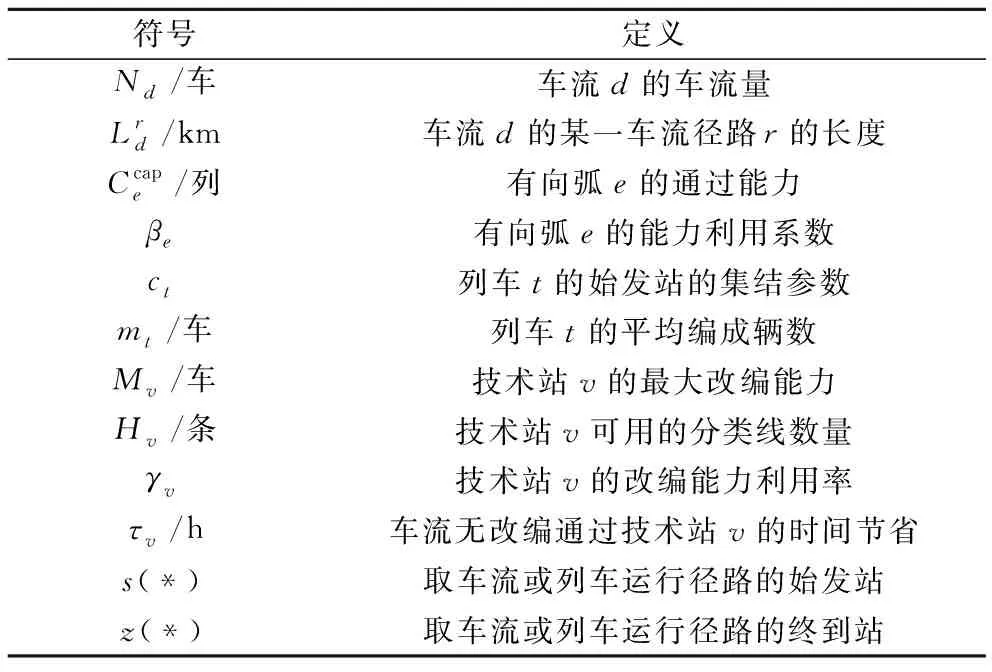
表3 参数符号及定义

表4 变量符号及定义
2.1 第一阶段——车流径路模型
(2)
(3)
(4)
(5)
(6)

目标函数式(2)第一项指车流选择不同径路时的总走行车小时消耗,第二项指车流完全改编车小时消耗,表示所有车流在其运行途中的每个技术站均进行改编时的车小时总和。由于车流总改编车小时消耗等于车流完全改编消耗减去车流无改编节省,而每支车流在每条径路下的完全改编车小时都是确定的,为了使总的车流改编车小时尽可能少,车流径路模型求解出的最终径路既要使车流走行总消耗少,也要使车流完全改编消耗尽可能少,同时,编组计划模型目标函数使车流无改编节省最大,两个模型的目标函数相加将能保证总的车流改编消耗最少。约束式(3)为径路唯一性约束,表示每支车流最终只能选择一条车流径路。约束式(4)为弧通过能力约束,弧通过能力以“列”为单位,每条有向弧代表一个单向站间区间,因此,流经任一有向弧的车流量不能超过其可用通过能力。
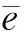
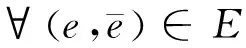
(7)
对于式(4)和式(7),模型任选一式即可。
2.2 第二阶段——编组计划模型
(8)
(9)
(10)
(11)
∀v∈V∀d∈D
(12)
(13)
xt=1 ∀t∈Ssuff
(14)
xt=0 ∀t∈Sforb
(15)
xt∈{0,1} ∀t∈P
(16)
(17)
wt∈N∀t∈P
(18)
式中:wt为列车t的车流所占用的分类线数,为非负整数;k为每条分类线一昼夜可服务的货车辆数,取值为200车/条[5-6],并规定每条分类线只能由一个编组去向的车组占用;M为一个很大的正数。
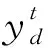
(19)
则每个编组去向占用的分类线数量为
(20)
因此,技术站的分类线约束为
(21)
式(21)为非线性约束,故引入辅助决策变量wt,因此,式(21)可线性化为
(22)
根据式(20),wt满足
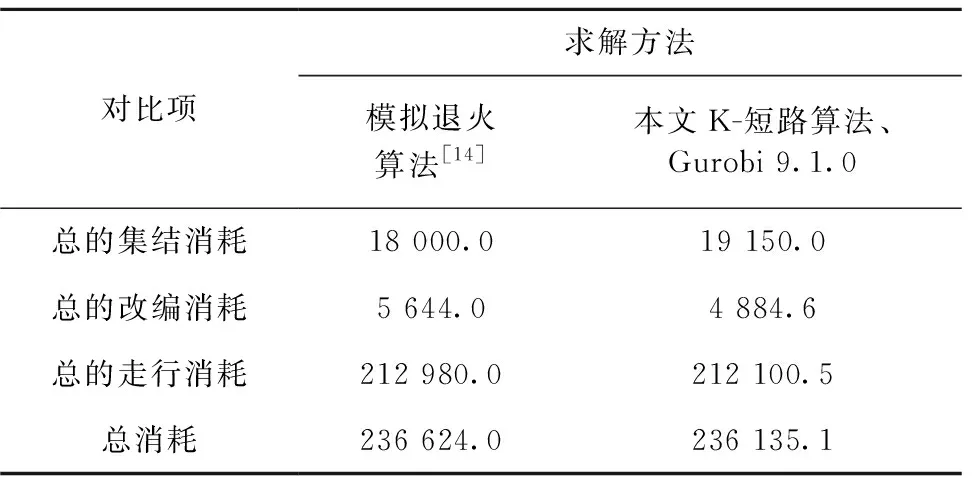
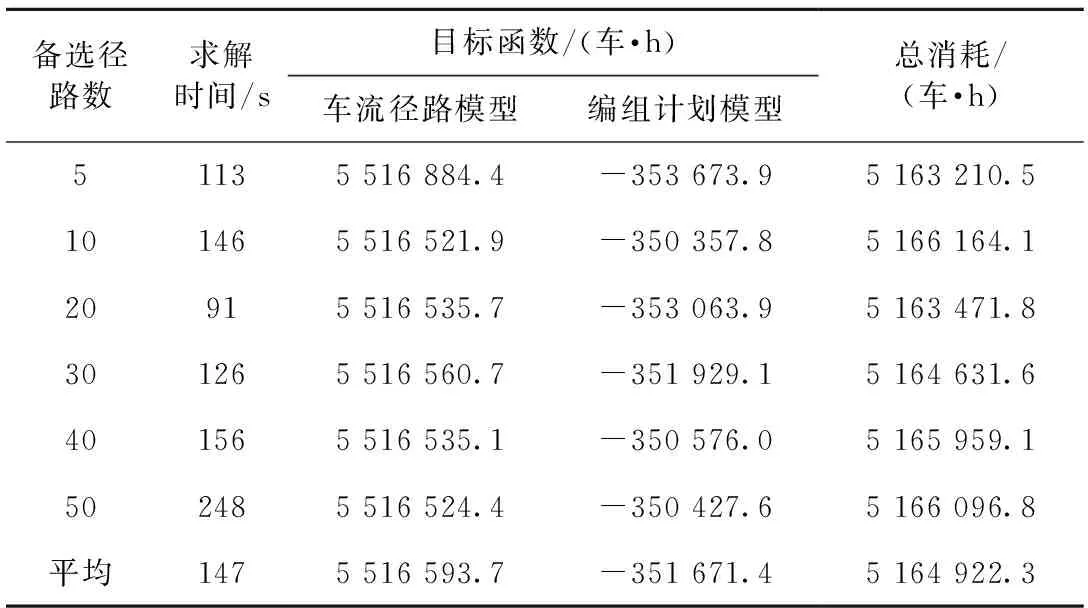
k(wt-1) (23) 式(12)为流平衡约束,能够保证两技术站间只有一种列车开行方案以及每支车流只选择一种输送方案,同时还能保证车流从始发站运输至终到站;式(13)为变量的逻辑约束,只有在列车开行的情况下,车流才能选择该列车;式(14)、式(15)分别表示满足必开和禁开条件时列车开行决策变量的取值;式(16)~式(18)分别表示列车开行决策变量、车流分配决策变量、辅助决策变量的取值范围。 经线性化处理后,模型整体为线性规划,可以通过功能强大的商业求解器或者传统精确算法求出精确解。模型的求解流程见图3。 图3 模型整体求解流程 表3 模型规模对比 分别以INFORMS 2019 RAS竞赛[14]中的8个技术站和32个技术站的路网对本文所提方法和模型进行求解验证。 8个技术站的小规模路网见图4,路网数据及参数均按照文献[14]要求设置,不考虑必开去向和禁开去向。在处理器为Inter(R) Core(TM) i7-9750 H 2.60 GHz,内存为16 GB,操作系统为Windows 10的Lenovo ThinkPad P53计算机上,用Python 3.7语言编程实现,并运用新一代大规模数学规划优化器Gurobi 9.1.0对提出的模型进行求解验证。 图4 小规模路网示意图 求解得到车流总的消耗为236 135.1车·h,最终开行34列列车,其中区段列车18列,直达列车16列。各技术站的改编能力及分类线使用情况见表4,各区间的通过能力利用情况见表5,最终的直达列车服务方案见图5,最终的车流分配方案见表6。 图5 最终的直达列车服务方案 表4 各技术站的改编能力及分类线使用情况 表5 各区间通过能力利用情况 表6 最终的车流分配方案 文献[14]求解结果与本文两阶段线性规划模型的求解结果对比见表7。其中,文献[14]基于模拟退火算法求解非线性综合优化模型,而本文采用精确方法求解线性模型,两者求解结果相比,本文总消耗减少了488.9车·h,结果表明本文所提方法和模型有效。 表7 小规模路网的求解结果对比 车·h 8个技术站的小规模案例已证明本文所提模型的可行性,为了更好验证和展示模型的求解效率和精确性,以文献[14]中32个站的大规模路网为例,路网共包括32个技术站,128个单向站间区间,992支车流,见图6。 图6 大规模路网示意图 由于该路网各技术站之间连接的复杂性和区间长度的特点,导致两技术站间满足绕道率μ=1.35的备选径路可能存在成百上千条,为了降低求解的复杂度,在满足绕道率的条件下,任意两技术站间的备选径路最多取20条,设置求解GAP为0.1%,其余参数不变,模型共耗时91 s得到最优解,车流总消耗为5 163 471.8车·h,较文献[14]所给结果共节省1 855车·h。 为研究模型的稳定性以及各OD对间备选径路数量对求解结果的影响,本文在求解车流径路模型时,每个OD对间满足绕道率的K-短路最多分别选5、10、20、30、40、50条。求解结果见表8,模型求解时间在91~248 s之间,平均耗时147 s,证明本文模型求解效率高且稳定;6次实验总消耗最大相差2 953.6车·h,平均总消耗为5 164 922.3车·h,较文献[14]平均节省404车·h,证明备选径路数量对本文模型的求解结果影响较小,同时也说明,在利用本文模型求解单组列车编组计划时,只需为每个OD对选取少量的备选径路便可得到近似最优解。 表8 各OD对间不同备选径路数对求解结果的影响 技术站列车编组计划作为货物列车编组计划的重要组成部分,规定了路网上所有技术站间的车流径路、列车的编成、到达站(或是装卸、解体站)以及列车的编组内容和编挂办法等,是车流组织计划,也是路网上各车站分工的战略部署[1],对发挥铁路运输能力,提高运输效率和经济效益有着重要作用,准确、高效地求解出符合运输需求的技术站列车编组计划对运输生产尤为关键。 本文基于多商品流服务网络设计原理,提出了列车备选集的构建方法,并建立了基于列车备选集的技术站单组列车编组计划两阶段线性规划模型,得到以下结论:①较车流递归方法,本文模型更加简单,能够直观展示车流的改编过程;②构建列车备选集可以限制每支车流只能分配到其最优径路生成的备选列车上,以此剔除不合理的车流分配变量,减小模型规模,加快求解效率;③将分类线约束有效转化为线性约束,既避免了复杂的非线性结构,也避免将分类线约束转化为最大编组去向数而造成与运输实际不符;④小规模和大规模路网的求解结果表明,本文模型能够快速、准确地得到最优解,求解结果质量优于非线性模型;⑤各OD对间不同备选径路数对本文模型求解结果影响很小,模型稳定可靠。下一阶段的研究将着重于车流径路和编组计划的综合协同优化,同时将分组列车纳入考虑,构建更加符合运输实际的编组计划模型。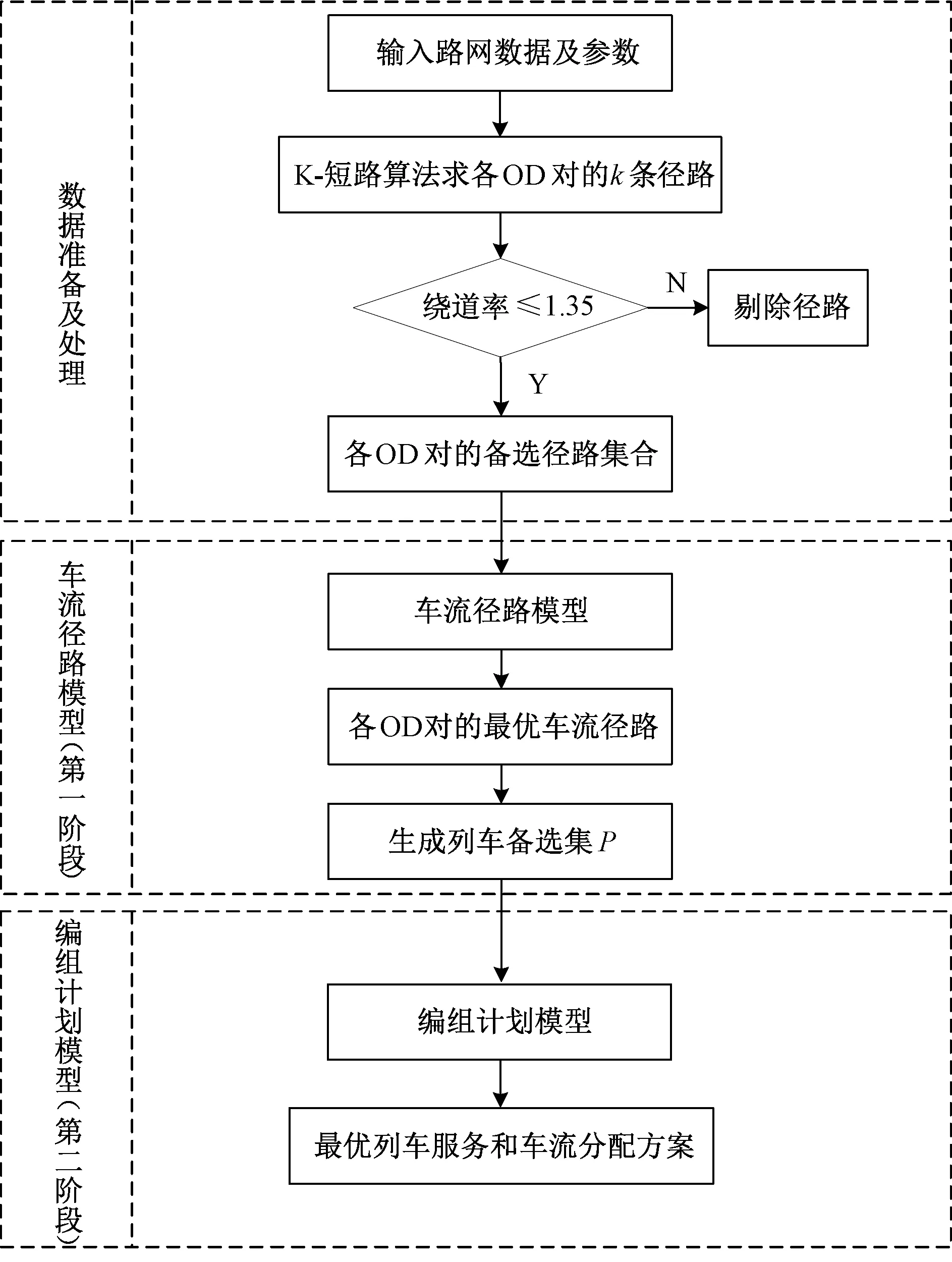
2.3 模型复杂度分析

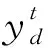
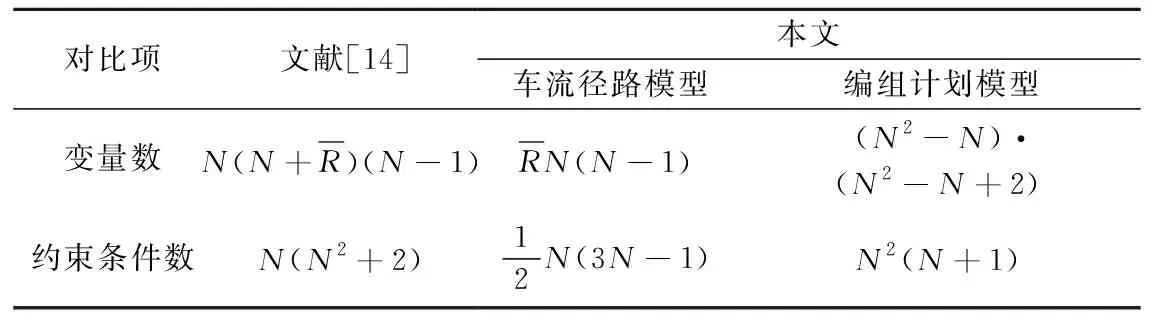
3 案例求解
3.1 小规模路网案例

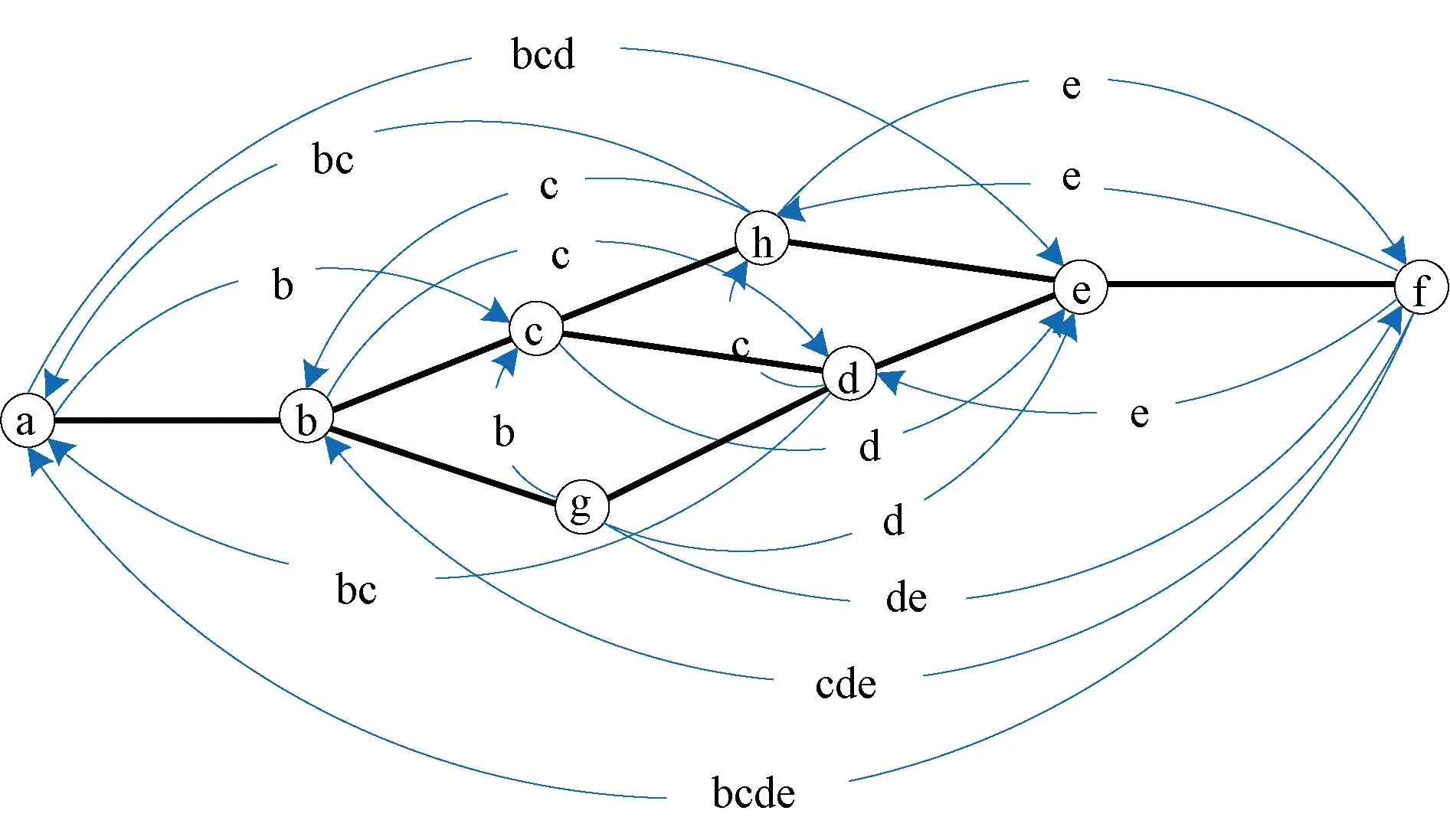

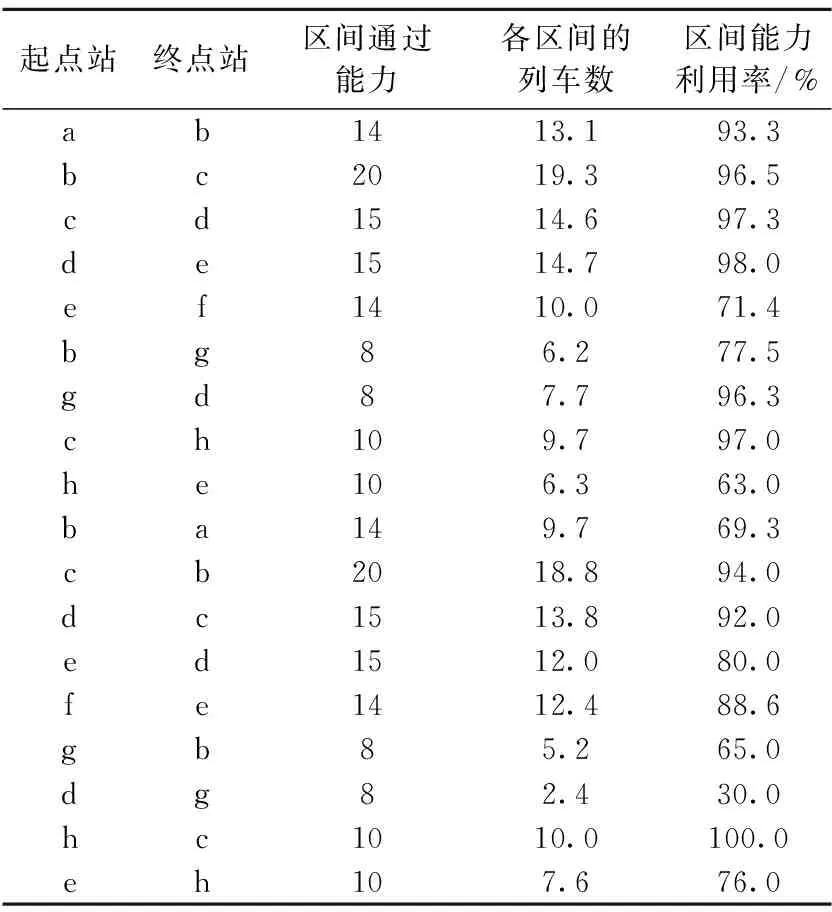
3.2 大规模路网案例

4 结论
