基于损耗模型的永磁同步电机高效控制参数敏感性分析

肖仁鑫，李健，贾现广

（650500 云南省 昆明市 昆明理工大学 交通工程学院）

0 引言

近年来，由于PMSM 具有结构简单、体积小、效率高、转矩电流比高、转动惯量低、控制性能好等诸多优点，被广泛用于各个领域[1-3]，因此，提高永磁同步电机的效率就显得尤为重要。永磁同步电机的损耗主要包括：铁损、定子电阻铜损、机械损耗及其杂散损耗。其中，机械损耗和杂散损耗属于不可控电气损耗，铁损和定子铜损属于可控电气损耗。

最小损耗控制的核心思想是在满足电机负载要求的情况下，通过控制电机的电流或者磁链，使得电机损耗降低，提高电机效率和功率因素[4]。目前，PMSM 常用的效率优化控制方法有基于损耗模型的控制（Loss Minimization Control）策略和基于搜索算法的控制（Search Control）策略两种[5-6]。基于搜索算法的控制策略是对逆变器直流输入功率进行采样，根据输入功率的变化，动态调节定子磁链或电流使电机在最小输入功率状态下工作，达到系统效率最优的目的[7]。效率搜索法一般有：黄金分割法、模糊搜索法、梯度法以及神经网络搜索法等，选用不同的算法可以直接决定系统的稳定性和响应效果[8-12]。基于搜索算法最小损耗控制方法的优点是不依赖电机参数且自适应能力强，算法的鲁棒性高，寻优精度较高[13-14]。但是，该控制方法的缺点是收敛时间长，在电机稳态运行下才可以启动搜索，不适用于频繁启动制动的动态场合；基于损耗模型的控制策略是建立电机的损耗模型，根据电机损耗模型方程得到目标函数，然后对目标函数求极值，求解最优工作点时的可控电气变量来控制电机。在矢量控制系统中，通常选择交直轴电流为控制变量[15-16]，简而言之，其核心思想是通过建立电机损耗数学模型推导出使电机损耗达到最小的定子电流或者定子磁链幅值来实现电机的效率优化[17-19]。基于损耗模型的优点是可以实现电机全局的效率最优化[20]，并且响应速度快，能够适用于各种场合[21]。但是，当电机在运行过程中，温度升高及其电枢绕组磁饱和会导致电机的参数发生变化，使得电机效率优化效果下降。

通过电机损耗的参数敏感性分析，为基于模型的电机高效率控制提供了重要参考。本文在搭建PMSM 的损耗模型后，根据公式推导出当前最优定子电流，使得电机的损耗功率最优。在此基础上，分别分析电机中的铁损电阻、铜损电阻及磁链对最优定子电流和总损耗功率的影响。

1 PMSM 损耗模型

本文采用表贴士永磁同步电机且仅考虑电机的可控电气损耗（铁损和铜损）。图1 所示为 d，q 轴旋转坐标系下带有铁损的永磁同步电机稳态时的等效电路图。

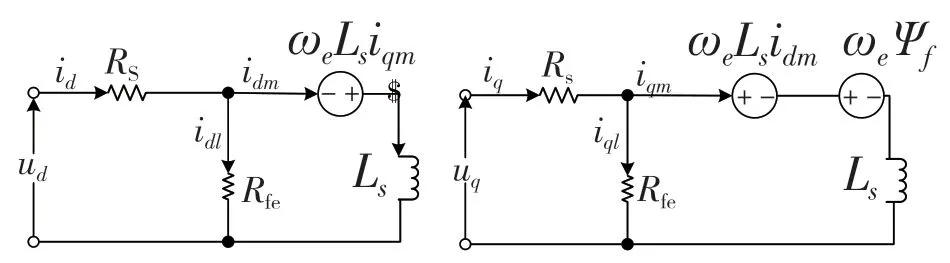
图1 永磁同步电机d、q 轴等效电路框图Fig.1 PMSM equivalent circuit in d,q axis coordinate system

由图1 中的d，q 等效电路图可知，Rs为永磁同步电机的三相定子绕组的电阻；Rfe为永磁同步电机的等效铁损电阻；ωe为永磁同步电机的转速；ψf为永磁同步电机的永磁体产生的磁链；id，iq分别为永磁同步电机的d，q轴定子电流分量；ud，uq分别为永磁同步电机的 d，q 轴定子电压分量；idm，iqm分别为永磁同步电机的d，q 轴定子电流的有功分量；idl，iql为分别为永磁同步电机的d，q 轴定子电流铁损分量；LS为永磁同步电机的电感且Ld=Lq=Ls。

在稳定状态下，根据图1 所示的等效电路图，利用基尔霍夫电压定律（KVL）得到永磁同步电机的回路电压方程

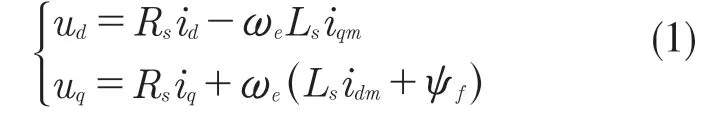
同时，利用基尔霍夫电流定律（KCL）得到永磁同步电机的节点电流方程

根据电路学知识可得永磁同步电机的d，q轴铁损电流分量

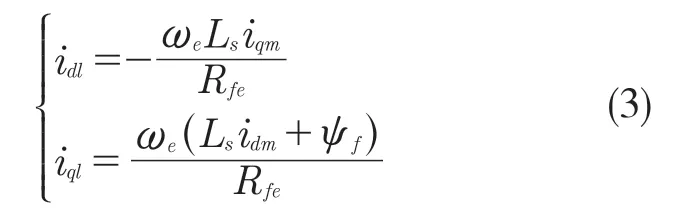
由上述公式可得永磁同步电机的d，q 轴定子电流铁损分量

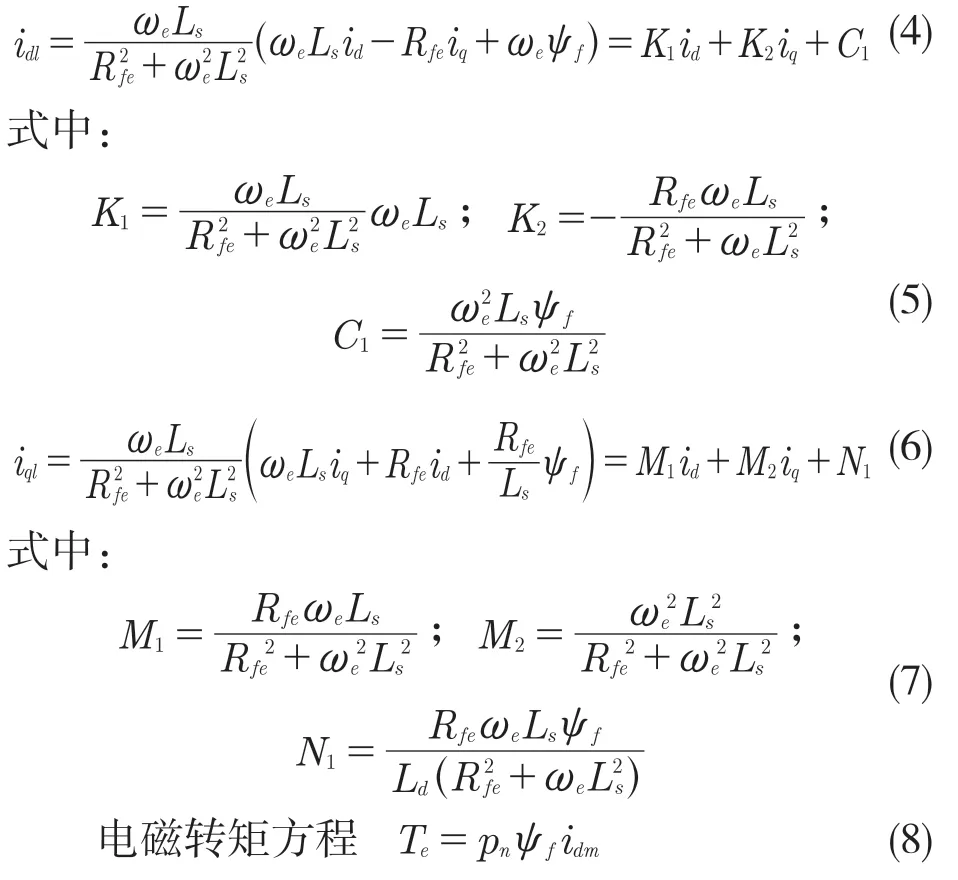
通过功率公式可得到永磁同步电机的铁损功率和铜损功率分别为

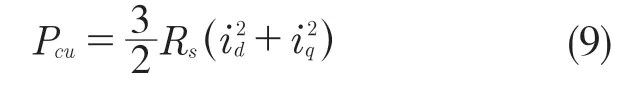
将永磁同步电机的d、q 轴定子电流铁损分量代入功率公式可得

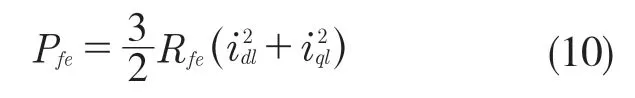
因此，在除掉不可控电气损耗机械损耗和杂散损耗后，永磁同步电机的电气损耗为

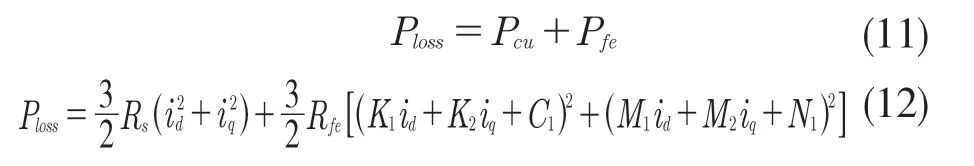
将永磁同步电机的参数代入上述公式，参数见表1。假设电机在运行过程中参数不发生变化，功率损耗函数Ploss是关于励磁电流id和iq的凸函数，可以寻找到1 组最优励磁电流，使得永磁同步电机的损耗达到最小。如图2 所示。

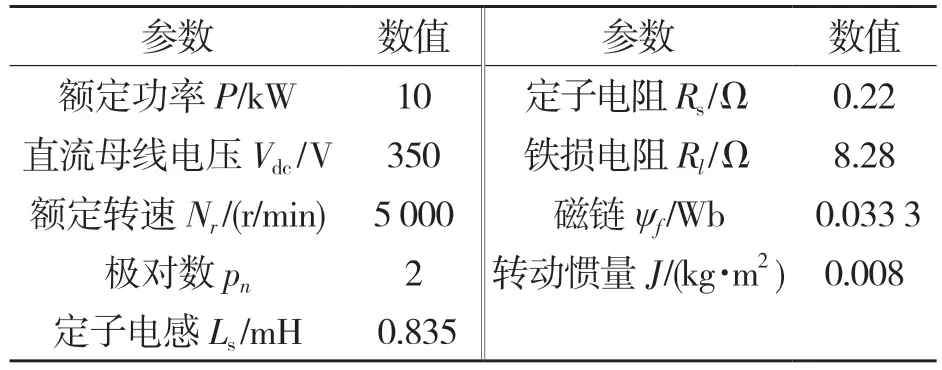
表1 电机参数表Tab.1 Motor parameters

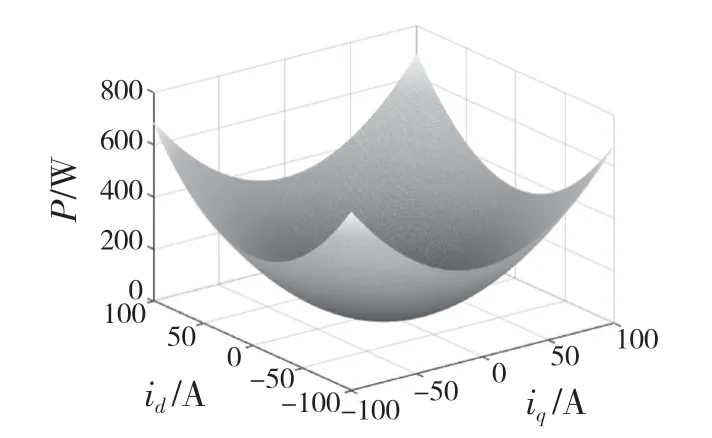
图2 电机可控损耗与d，q 轴电流关系损耗Fig.2 Controllable loss of motor and loss in relation to d,q axis current

2 推导PMSM 定子励磁电流

将式（8）代入式（9）以及式（10）中消去iqm，得到的Ploss是关于到idm，Te以及ωe的函数。在永磁同步电机达到稳态工作点时，Te和ωe是常数，可控电气功率损耗Ploss是关于idm的一元二次函数方程，要使得可控电气功率损耗最小也就变成一个二次函数求极值的数学问题。通过一元二次函数性质，可以寻找到一个最优电流idm，同时使得永磁同步电机可控电气损耗功率之和达到最小。通过求导，可得最优电流分量

通过以上公式可以发现，如定子励磁电流 id满足式（14），则可以找到永磁同步电机在运行中的最小可控电气损耗功率。通过方程式可以求出当前工况下永磁同步电机可控电气损耗功率下的最优定子励磁电流，从而使得永磁同步电机系统工作效率最高。

3 基于损耗模型效率最优仿真分析

损耗模型（LMC）效率最优化控制策略的核心思想是电机在稳态工况下，根据电机的等效电路方程建立系统的损耗模型方程，根据方程计算出各种损耗与定子电流之间的关系，最后利用数学求极值的思想，找到最优的励磁电流经过PI调节器的调节，从而实现电驱控制系统的效率最优。其控制框图如图3 所示。

永磁同步电机的仿真参数如表1 所示。该仿真模型是在矢量控制id=0 的基础上，加入了损耗模型模块，与传统的id=0 不同点在于，d 轴的电流分量是根据永磁同步电机输入的电角度、磁链、转矩、转速等经过计算得到的最优定子励磁电流，然后将得到的最优定子励磁电流输入到损耗模型中，降低损耗模型功率，提高电机的效率[22]。仿真条件设置：负载转矩为2 N·m，转速为5 000/min，在0.5 s 时，加入基于损耗模型效率最优控制策略。图4 和图5 所示为加入损耗模型前后d 轴定子励磁电流和损耗模型的变化。通过仿真结果图4 得知，在0.5 s 后加入损耗模型，最优定子励磁电流为-14.3 A。如图5 所示，电机的可控电气损耗功率由id=0 时的510.8 W 变成了446.9 W,可控电气损耗减少63.9 W，损耗下降12.5%。因此，基于损耗模型法效率最优控制策略相较于传统的id=0 可以有效降低永磁同步电机的可控电气损耗，从而使永磁同步电机系统在运行过程中能够保持较高的效率。

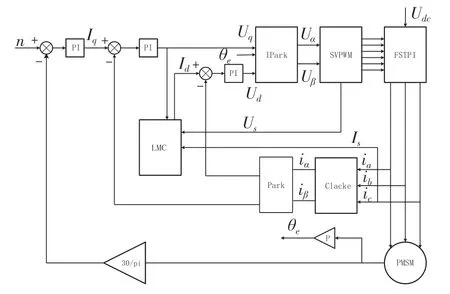
图3 基于损耗模型法永磁同步电机效率最优控制框图Fig.3 Efficiency optimal control block diagram of permanent magnet synchronous motor based on loss mode

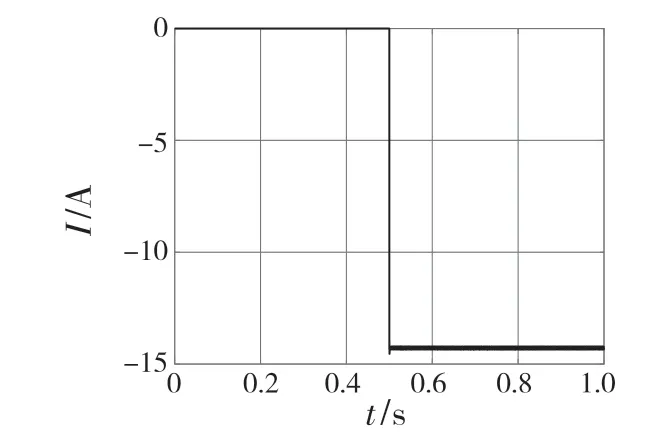
图4 最优定子励磁电流Fig.4 Optimal stator excitation current

图5 总可控电气损耗Fig.5 Total controllable electrical loss

4 参数敏感度分析

通过式（14）发现，永磁同步电机的最优定子励磁电流的大小与电机的参数（定子绕组电阻、电感、等效铁损电阻和磁链）存在一定关系，这几个参数均容易受到温度、磁饱和及负载变化影响。通过电机损耗的参数敏感性分析，为基于模型的电机高效率控制提供了重要的参考。下面将对损耗模型的中铁损电阻、铜损电阻以及永磁体磁链进行仿真验证并分析。

4.1 铁损电阻变化在损耗模型中的影响

在损耗模型中，仿真得到最优定子励磁电流为-14.3 A，总可控电气损耗功率为446.9 W。其他参数不变的情况下，转矩为2 N·m，将等效铁损电阻变为原来的0.8 倍和1.2 倍，进而得到等效铁损电阻变化后的最优定子电流和总可控电气损耗功率。图6 所示为铁损电阻变化后最优定子励磁电流，图7 所示为铁损电阻变化后总可控电气损耗功率。当铁损电流为原来的0.8 倍时，总损耗功率为448.6 W，比原来增加1.7 W，总损耗效率相对原来增加0.4%；当铁损电阻为原来的1.2 倍时，总功率为442.4 W，比原来减少4.5 W；铁损电阻变为原来的1.2 倍时，总损耗效率相对原来增加1%。

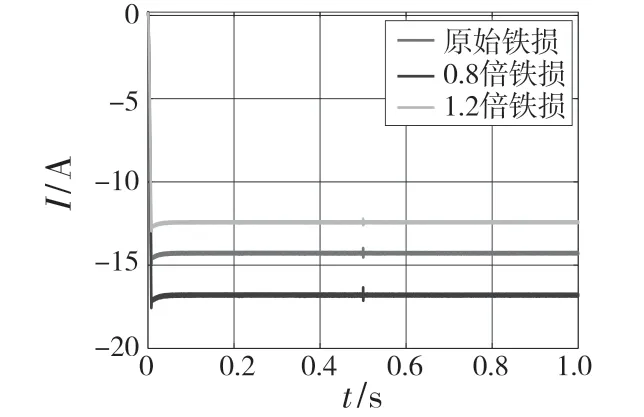
图6 铁损电阻变化最优定子励磁电流Fig.6 Optimal excitation current of stator with change of core loss resistance

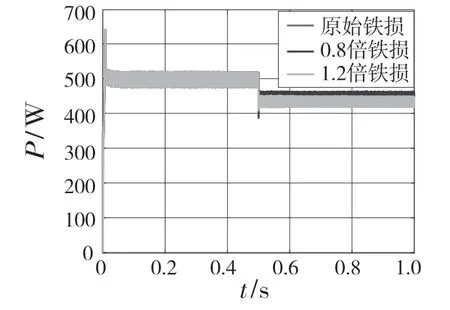
图7 铁损电阻变化总损耗功率Fig.7 Total loss power of iron loss resistance change

4.2 铜损电阻变化在损耗模型中的影响

在损耗模型中，仿真得到最优定子励磁电流为-14.3 A，总可控电气损耗功率为446.9 W。其他参数不变的情况下，转矩为2 N·m，将铜损电阻变为原来的0.5 倍和1.5 倍，进而得到铜损电阻变化后的最优定子电流和总可控电气损耗功率。图8 为铜损电阻变化后最优定子励磁电流，图9为铜损电阻变化后总可控电气损耗功率。

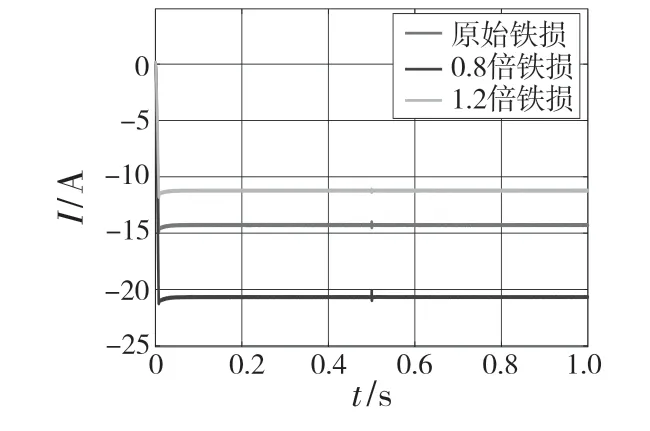
图8 铜损电阻变化最优定子励磁电流Fig.8 Optimal stator excitation current with copper loss resistance change

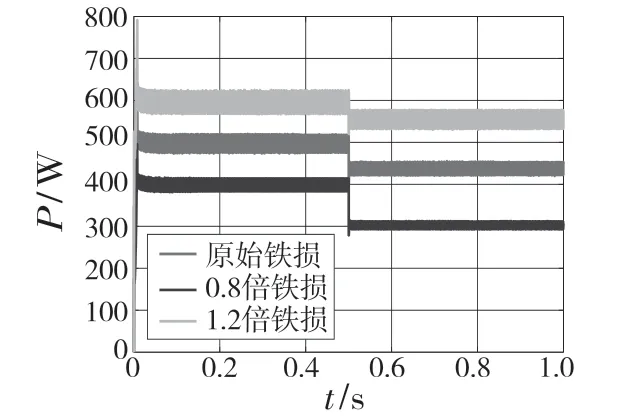
图9 铜损电阻变化总损耗功率Fig.9 Total loss power with copper loss resistance change

当铜损电阻为原来的0.5 倍时，损耗功率为304.9 W，损耗效率相对原来提高32%；当铜损电阻为原来的1.5 倍时，最优定子电流为-11.3 A，损耗功率为569.9 W，损耗效率相对原来下降约28%。

4.3 磁链变化对损耗模型中的影响

在损耗模型中，仿真得到最优定子励磁电流为-14.3 A，总可控电气损耗功率为446.9 W。其他参数不变的情况下，转矩为2 N·m，假定磁链的额定值变为原来的1.2 倍和1.4 倍，观察得到最优定子励磁电流和总可控损耗电流曲线。图10 所示为磁链变化后最优定子励磁电流，图11 所示为磁链变化后总可控电气损耗功率。当磁链为原来的1.2 倍时，损耗功率为450.6 W，损耗效率相对原来下降约0.8%。当磁链为原来的1.4 倍时，损耗功率为453.2 W，损耗效率相对原来下降约1.4%。

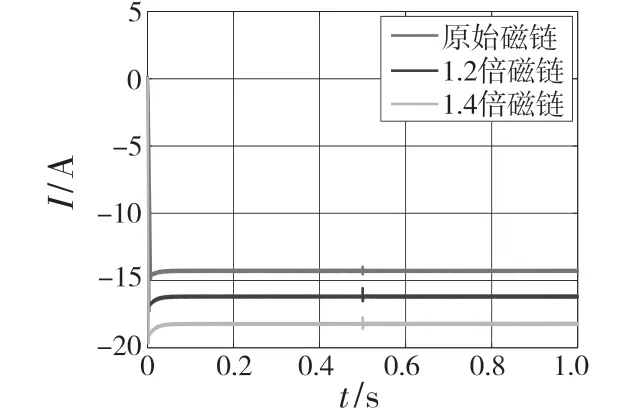
图10 磁链变化最优定子励磁电流Fig.10 Optimal stator excitation current with flux change

5 结束语

本文通过PMSM 损耗模型，推导出了最优定子励磁电流使得电机的损耗最低，并与传统的的矢量控制进行对比，通过仿真结果证明，应用损耗模型最优控制可以有效降低永磁同步电机的损耗。最后，在此基础上对电机的参数进行了敏感度分析，得到结论：当永磁同步电机铁损电阻增大时，损耗模型的功率会减少，其效率增加；当永磁同步电机铜损电阻和磁链增大时，损耗模型的功率会增加，其效率会下降。