某球型密封中橡胶圈的受力变形研究

2021-04-02梅杰卢曦

农业装备与车辆工程 2021年3期

梅杰，卢曦

（200093 上海市上海理工大学机械工程学院）

0 引言

随着密封技术向高压、高速、高温和大直径等方向发展，密封件的变形问题变得更突出，密封端面如果发生变形，会导致端面产生间隙，进而发生泄漏问题，端面上发生局部应力集中也会导致局部过度磨损和高温，影响整个端面的密封性能[1-2]。

目前国内对于密封件中的橡胶圈的变形研究比较少，其中大部分的研究都是通过有限元模型分析O 型橡胶圈，而对V 型橡胶圈的研究更少。文献[3]为了将端面比压值准确地应用到机械密封的安装或维修过程中，研究机械密封端面比压与变形量的关系；文献[4]针对3 种机械密封结构模型，利用ANSYS 有限元分析软件，模拟机械密封摩擦副端面的变形，讨论了橡胶O 型密封圈不同受力边界条件下机械密封端面变形的规律。

传统的密封结构计算和设计都是假定端面中完全接触，忽略了变形的差异，不能较准确地反应密封胶圈的变形问题，本文通过构建V 型橡胶圈的理论模型建立了载荷与接触面位移的关系，再通过有限元分析该橡胶圈的变形情况，并验证该模型的准确性，对密封结构的分析具有一定的理论和现实意义。

1 结构及理论计算模型

1.1 结构模型

该球型密封结构如图1 所示，包括压盖、2辅助密封圈、V 型密封圈、锁片和球笼式等速万向节。球笼式等速万向节又包括钢球、钟形壳、保持架和星形套；压盖的作用是挤压和固定胶圈，也能防止发生内部漏油的情况；辅助密封圈的作用是传递压盖的挤压力来固定V 型密封圈，使其减小轴向位移；V 型密封圈与下方的V 型支撑环紧密贴合，支撑环支撑V 型密封圈、对V 型密封圈的位置起决定性作用，稳定并保护密封圈。V 型密封圈在密封结构中具有较好的密封可靠性，使用寿命长且方便调节。本文所研究的V 型密封圈内部有一个L 型金属骨架，金属骨架是用以加强密封圈的刚度，根据使用要求的不同，金属骨架放置的位置也有所不同。这种金属骨架埋入式密封可以防止金属骨架生锈，也可以避免在高温时与橡胶的配合强度降低[5-6]。

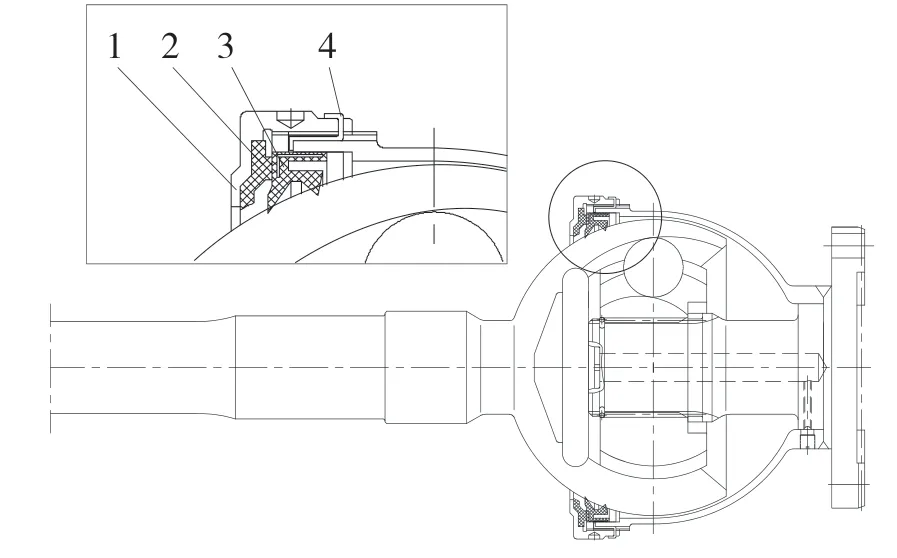
图1 球型密封结构Fig.1 Spherical seal structure

在V 型密封圈和辅助密封圈安装好后，把压盖贴紧辅助密封圈侧面，再通过压紧装置压紧密封圈。压紧装置通过对V 型橡胶圈施加垂直于接触面方向向下的载荷，挤压橡胶圈贴紧支撑环来达到提高密封性的作用。由于V 型橡胶圈内部有金属骨架，硬度提高，不易发生变形，现只考虑金属骨架下方的部分。

1.2 理论计算模型

在构建载荷的理论计算模型时，根据该密封件的密封原理和实际工作情况进行系列假设如下：（1）带有金属骨架的胶圈部分假设为绝对刚性，V 型橡胶圈与下方的V 型支撑环紧密贴合，所以V 型橡胶圈的下方可作为固定的约束边界；（2）V 型圈受挤压发生的变形较均匀；（3）V型橡胶圈在受挤压变形过程中只发生截面挤压变形，不发生拉伸变形；（4）不考虑润滑与内压的影响。

通过分析O 型圈的轴向力经验公式[7]，考虑到本文中的V 型橡胶圈同样受橡胶自身因素的影响，比如弹性模量、变形率、接触面积等。现以统一量纲为原则，引入影响系数K，有公式：

式中：Q——载荷；E——弹性模量；W——变形率；S——密封圈接触面面积。其中，V 型橡胶圈的变形率W 可由式（2）表示：

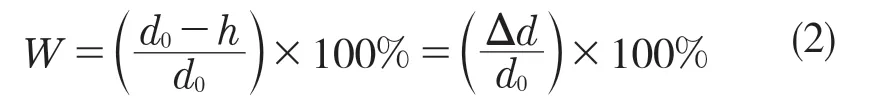
式中：Δd——V 型橡胶圈的变形量。

联立式（1）与式（2）求解载荷公式如下：

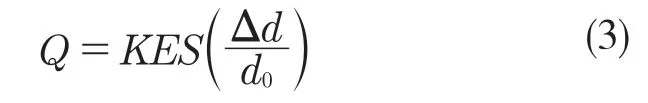
其中，接触面积的确定需要大量试验来修正，影响系数K 在小变形的情况下取1～3。

2 V 型橡胶圈的有限元分析

2.1 橡胶材料系数的理论估算

橡胶材料作为一种高分析非线性超弹性材料广泛应用于各种密封件中。材料特性的非线性和几何非线性让橡胶材料的研究变得非常复杂，所以利用有限元仿真软件ANSYS 中的高阶Mooney-Rivlin 本构模型来描述V 型圈的力学行为。Mooney-Rivlin 模型是基于材料变换理论和不可压缩各向同性超弹性材料的Mooney 有限变形弹性理论。超弹性材料的本构关系用应变密度函数描述。

Mooney-Rivlin 超弹性模型的应变能密度函数[8]如下：

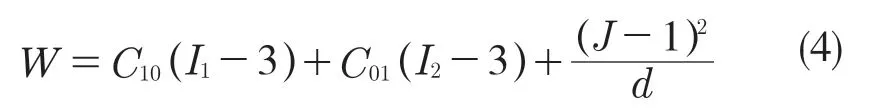
式中：I1，I2——应变不变量；C10，C01——Mooney-Rivlin 常数；d——常数，可由C10，C01及泊松比确定；W——应变能密度函数。

令C10为C1，C01为C2，对于不可压缩性橡胶材料其μ为0.5，其泊松比μ、弹性模量E 和材料系数有以下关系式[9]：

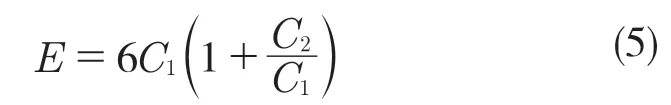
根据橡胶硬度HS 与弹性模量E 的实验数据拟合得到两者之间的关系式[8]:

综合式（5）、式（6）得关系式如下：

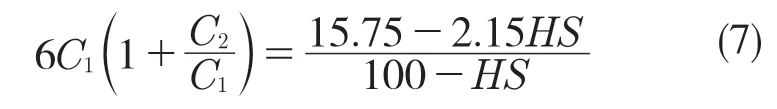
通过式（7）可以发现，橡胶的弹性模量可以通过测橡胶的硬度来得出，材料的系数C1与C2的值可以通过确定C2/C1的值来确定。

2.2 V 型橡胶圈有限元分析模型

现通过试验测得V 型橡胶圈的硬度为76，代入式（6）得弹性模量E 为7.8 MPa。由于模型较复杂，在ANSYS 建模分析中采用四面体单元solid187。

所建模型的截面图如图2 所示。实物模型如图3 所示。

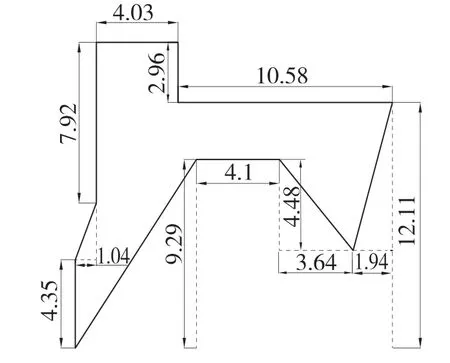
图2 V 型橡胶圈截面图Fig.2 V-type rubber ring side image

图3 V 型橡胶圈有限元模型图Fig.3 Finite element model image of V-type rubber ring

为方便该密封结构的仿真分析，做以下简化：（1）载荷在橡胶接触面上均匀分布；（2）V 型橡胶圈两边尖端点在橡胶受挤压时一直在支撑环面上，没有溢出；（3）只考虑橡胶圈在径向上的高度变化和轴向上的厚度变化。故对模型的边界条件做如下处理：V 型橡胶圈的上表面施加均匀的面载荷；在V 型橡胶圈的下方，与支撑环接触的表面施加固定约束；对V 型橡胶圈的左右两侧表面施加只沿轴向的自由位移，其余方向的限制位移。

2.3 V 型橡胶圈变形的有限元分析

为了确定合适的C2/C1的值，现给出3 组不同的C2/C1值[10]并计算出各组下的C1与C2值，如表1 所示。

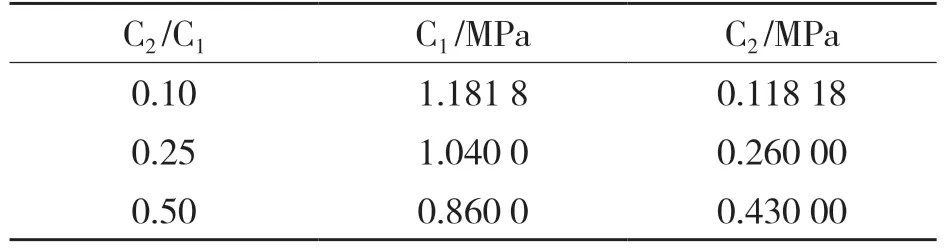
表1 橡胶在不同C2/C1值下的C1与C2的值Tab.1 Values of rubber C1and C2under different C2/C1values

选取V 型橡胶圈截面图上的2 个平面位置，如图4 所示。选取上侧平面，在不同的C2/C1值下，施加不同的载荷，仿真计算橡胶圈在上侧平面位置处的极限位移。

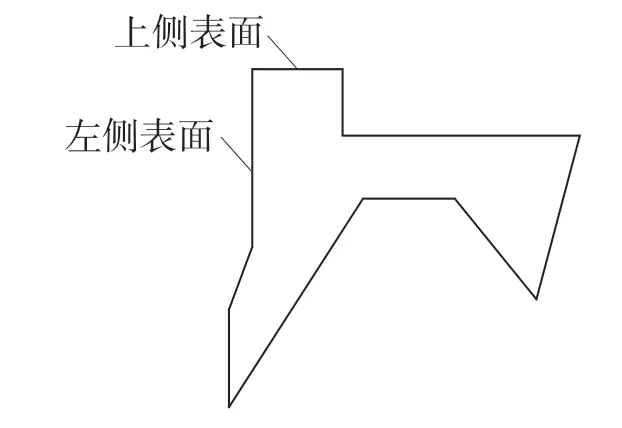
图4 两平面位置分布图Fig.4 Two-plane location image

这种具有往复运动的V 型橡胶圈在高速运动中所能承受的压力范围为0～20 MPa[11]，但具体的压力范围受自身结构的影响，为保证橡胶受挤压变形不被破环，有合适的变形率，现取载荷范围为0～10 MPa，并在范围内均匀地取10 个载荷数值，在有限元软件中对橡胶圈施加以上数值，并记录不同C2/C1值下的各个表面的位移值。绘制的载荷位移变化曲线如图5 所示。

从图5 可以看出，当C2/C1值为0.1，0.25，0.5 时，上侧表面的位移量都小于5 mm，可以发现C2/C1值对仿真结果的影响较小。因此在变形量小于5 mm 的前提下，分析不同节点处的载荷—位移关系时，C2/C1值为0.25 对应的曲线在3 条曲线的中间位置，所以一般计算可酌情选择这个值[10]。根据橡胶圈上2 个表面的分析结果，对应的不同载荷与位移量的关系曲线如图6 所示。

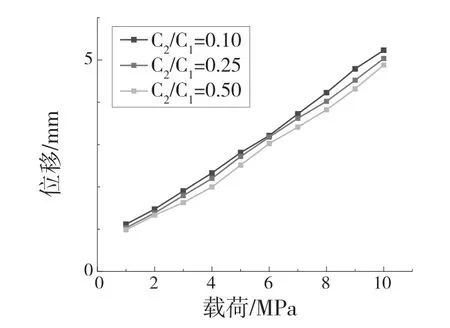
图5 上侧表面在不同C2/C1值下的载荷—位移曲线Fig.5 Load-displacement curve of upper surface at different C2/C1values

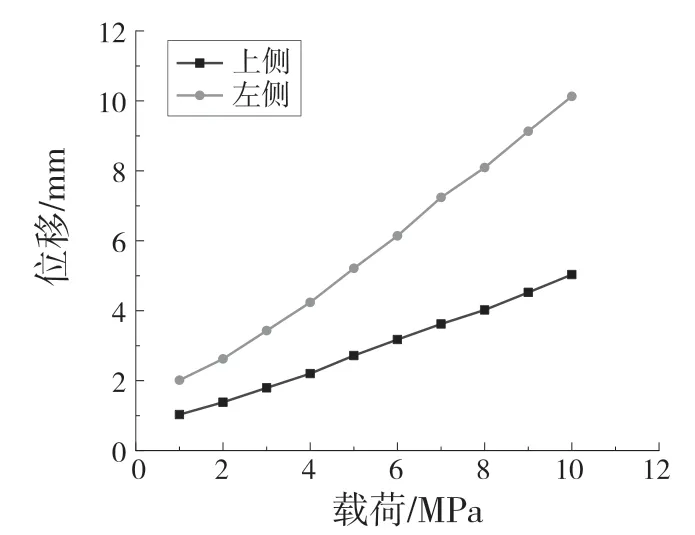
图6 两侧面的载荷—位移变化曲线Fig.6 Loads-displacement change curve on both sides

通过分析载荷与位移变化曲线能够看出，该橡胶圈在载荷较小的情况下会发生小变形；在受到相同载荷的情况下，侧表面的变形更加突出，对辅助橡胶圈的挤压更加严重，具体的侧表面变形情况如图7 所示。

图7 两侧表面变形图Fig.7 An image of surface deformation on both sides

图7 展示出V 型橡胶圈在受到载荷后的变形剖面图，能够看出V 型橡胶圈左侧面受到较大的变形，这会对辅助密封圈产生较大的挤压和冲击，使两橡胶圈的间隙逐渐减小，增加了密封圈之间的摩擦，使密封性能得到更好的提高，但是也缩短了胶圈的使用寿命。

另外，分析上侧表面的变形与载荷的变化曲线，可以发现上侧表面位移量与载荷近似线性，对图中的曲线用最小二乘法拟合公式如下，满足形式简单、方便计算和符合误差范围的要求。

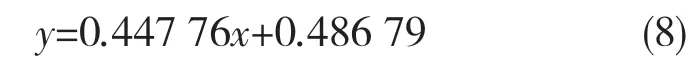
式中：x——橡胶圈上侧表面施加的载荷，MPa；y——橡胶圈上侧表面的位移量，mm。

通过式（8）能够将设计阶段的载荷直观地反应为胶圈的变形情况，从而为密封件的安装和压紧提供一定的指导意义，能够避免经验方法的安装带来的不确定性，同时也增加了安装的合理准确度，提高了密封的有效性。

为验证该理论模型的适用性，现将小变形下理论计算结果与有限元分析计算结果进行误差分析，见表2。

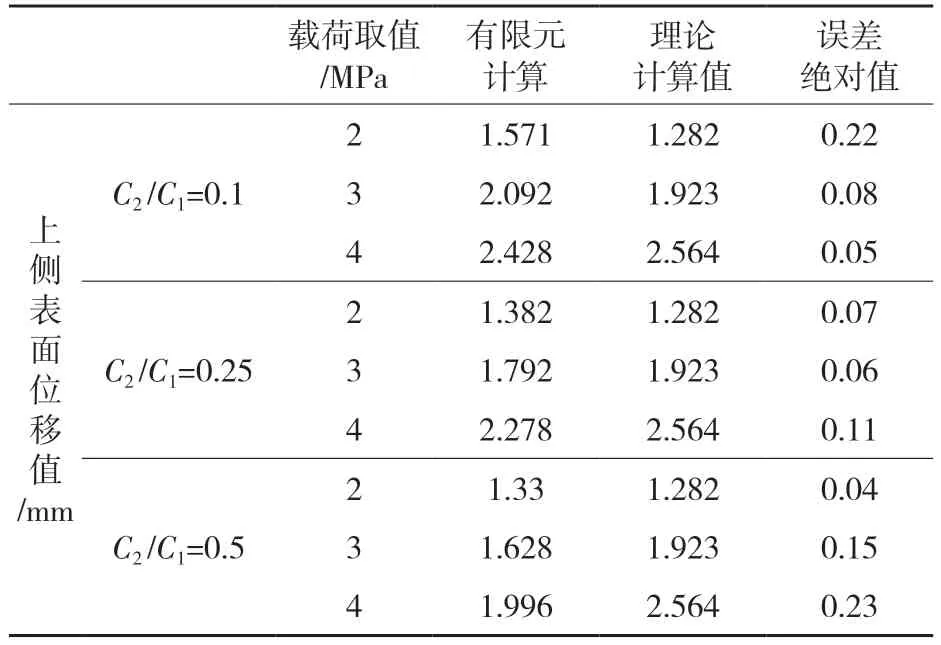
表2 仿真分析与理论计算之间的误差Tab.2 Errors between simulation analysis and theoretical calculations

通过表2 发现，当比值为0.1，载荷取2 MPa 时，误差为0.22 较大；比值为0.5，载荷取4 时，误差为0.23 较大；比值为0.25 时，误差值整体较小，相对于其他的比值，该比值更具可靠性，故选择0.25 比值的有限元模型材料材料系数。同时经检验，此理论计算值与有限元计算误差在10%以内，可以通过该理论模型建立载荷与变形量之间的联系。