基于改进的BP 神经网络胶铆接头的力学性能预测研究

2021-04-02刘文杰邢彦锋陆瑶

农业装备与车辆工程 2021年3期

刘文杰，邢彦锋，陆瑶

（201620 上海市上海工程技术大学机械与汽车工程学院）

0 引言

由于轻型材料与钢板的混合连接能够有效降低车身质量，提高汽车的燃油经济性能与汽车动力性能，已成为今后车身结构的发展方向[1]。自冲铆接技术具有工艺简单、外观美观等特点[2]，广泛应用于异种材料的连接。将结构胶接与自冲铆接技术结合形成的胶铆技术应用于车身连接中，既可以改善胶接技术的裂缝延伸、瞬间失效等问题，也缓解了铆接导致的集中应力过大、连接强度不稳定等问题[3]。

针对自冲铆接及胶铆工艺，国内外学者进行了大量研究。Fabrizio[4]对比了铝合金自冲铆接、胶接及胶铆接头的力学性能，发现低循环次数下，混合接头的性能比普通胶接接头差，而高循环次数下，混合接头的性能要好得多。并且，相对于粘结接头，混合接头中机械紧固的存在显著降低了粘合剂层中的裂纹扩展速率，因此疲劳寿命更长；刘洋[5-6]等制备了5052 铝合金以及钛合金和8090 铝锂合金的自冲铆接单搭接接头和粘接-自冲铆复合接头，通过力学试验获得各组接头的失效载荷，并计算了各组接头的能量吸收值，发现粘接剂可以提升自冲铆接接头的力学性能；周江奇[7]等研究了结构胶对自冲铆接接头成型过程的影响规律，发现结构胶能够在接头成型过程中减小铆钉的铆接力，使得胶铆接头的扩张程度小于自冲铆接接头；李明彬[8]等制作了一种新型耐高温复合材料2D-C/SiC 的胶铆接头，并研究了不同搭接宽度下接头的力学性能，发现接头失效模式均为胶层截面破坏以及铆钉剪切破坏，且胶层界面首先发生开裂。

反向传播神经网络，简称BP 神经网络（BPNN），这是一种基于误差反向传播的多层前馈网络，该算法在求解非线性连续函数时，通过不断改善多层前馈神经网络权重，能够快速有效地逼近原始结果[9-11]，但会存在一些缺陷：（1）学习收敛速度慢；（2）局部极小问题；（3）网络结构选取尚无理论依据，只能根据经验选取。遗传算法（Genetic algorithm）是模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优化方法[12-14]。该算法从多个初始点并行运行，能够改善BP 神经网络的训练缺陷。

目前，胶铆接头的质量评价方法主要为破坏性试验和在线监测[15]方法，不具有可预测性，因此，寻找一种可靠的胶铆接头的质量预测模型具有较大意义。本文利用遗传算法优化BP 神经网络的连接权值和阈值，并将遗传算法改进的BP 神经网络（GA-BPNN）应用于胶铆接头的力学性能预测中，建立了胶铆接头最大拉剪力预测模型，最后通过试验验证了该模型的精确度。

1 胶铆连接的工艺过程

胶铆工艺是在铆接之前使用胶粘剂对工件进行粘接，之后再使用铆接工艺进行铆接，包括表面处理、涂胶、铆接、固化4 个步骤进行。其中的铆接步骤为普通的铆接工艺，用于连接两种或两种以上金属板材的冷机械连接工艺。铆接工作过程为：首先将压边圈及铆钉下降到与板件接触的位置，将板件夹紧固定；然后在动力的推动下，冲头下降，推动铆钉刺穿；接着铆钉被进一步推入板件，铆钉腿部张开形成机械互锁，将板件固定在一起；最后达到预定的行程后，冲头与压边圈卸载对板件的夹紧力并回到初始位置。图1 所示为自冲铆接工艺过程依次为夹紧、刺穿、扩张、卸载4 个阶段。

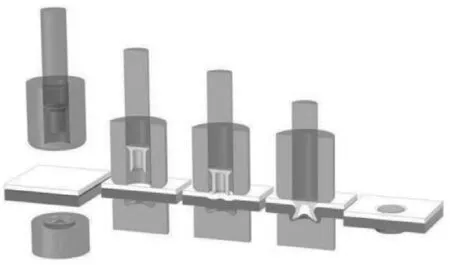
图1 自冲铆接工艺流程Fig.1 Self-piercing riveting process

2 胶铆连接试验

本研究使用的材料是AA6111 铝合金板和DP780 高强度钢板。板材力学性能如表1 所示。铆钉长度为6 mm，凸台凹模的深度为2 mm，内部底径为8.8 mm。本文选择的结构胶粘剂为ET5429，胶粘剂具体属性如表2 所示。

表1 板材力学性能Tab.1 Mechanical performance of the plates

表2 胶粘剂物理属性Tab.2 Adhesive physical properties

使用的液压铆接设备如图2（a）所示。胶铆试样如图3 所示，使用的叠加组合为上层钢板+下层铝板，红色阴影为涂胶区域，胶层厚度为0.1 mm，在涂胶时，撒上直径为0.1 mm 的玻璃珠控制胶层厚度。使用万能拉伸试验机对接头拉伸力进行测量，拉伸速率为0.5 mm/min，如图2（b）所示。进行拉伸试验时，夹持宽度为30 mm，并在试件两端添加了相同厚度的垫片，以保证实验时拉伸力方向与板料保持平行。

图2 铆接及拉伸实验设备Fig.2 Self-piercing riveting and tensile testing machine

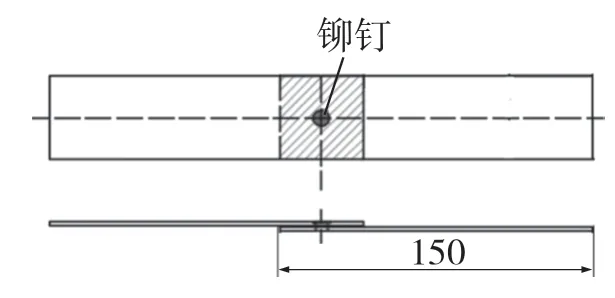
图3 胶铆接头试样Fig.3 Riv-bonding joint sample

3 GA-BP 神经网络预测模型

3.1 算法参数的确定

由于GA-BP 神经网络是在BP 神经网络模型的基础上改进的，因此，需要构建基于BP 神经网络的胶铆接头力学性能预测模型。神经网络参数包括神经元个数、隐含层数、隐含层神经元个数及传递函数等。

BP 神经网络结构包含1 个输入层、1 个或多个隐含层和1 个输出层。结合胶铆接头力学性能的课题，输入层中神经元个数为3，分别为铆接压强、搭接宽度和铝板厚度。输出层神经元个数是1，为胶铆接头最大拉剪力。随机改变铆接压强、搭接宽度和铝板厚度，共获得了100 组胶铆接头的最大拉剪力，其中部分数据如图4 所示。

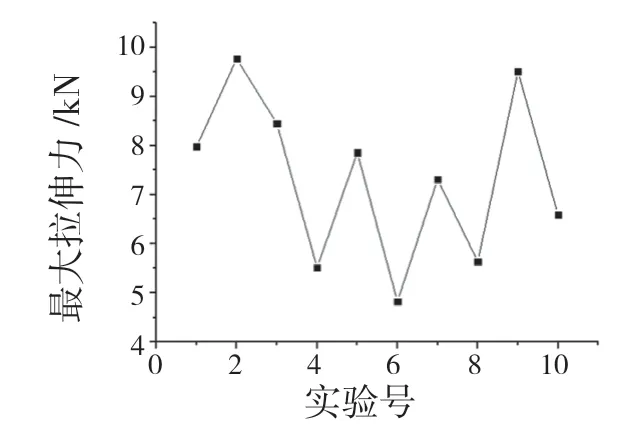
图4 最大拉剪力部分数据Fig.4 Partial data of maximum tensile force

在数据训练之前，首先使用式（1）对数据进行归一化处理。

式中：xmin——数据序列中的最小数；xmax——数据序列中的最大数。

归一化处理后，将前90 个数据作为训练样本，用来训练适合应用于分析胶铆参数和胶铆接头最大拉剪力的关系的预测模型，后10 个数据作为测试样本，用来验证所获得的胶铆接头最大拉剪力预测模型。

本文采用经典三层网络结构，即隐含层只有一个。隐含层节点数是决定BP 神经网络预测精度的关键因素，从而决定了胶铆接头最大拉剪力的预测精度。通常带有单个隐层的神经网络确定隐含层中神经元数量可以使用经验式（2）进行计算。通过式（2）计算隐含层神经元个数在3～13 之间。因此，本文不断改变隐含层神经元数目，并代入神经网络训练，得到在不同隐含层神经元个数下的均方误差如图5 所示。

式中：p，q——输入层和输出层中的节点数；a——取值范围为1～10 的常数。

从图5 中可以看出，当隐含层神经元个数为5 个时，均方误差最小，因此，本文所选择的隐含层神经元个数为5。本文的胶铆接头最大拉剪力预测模型网络结构如图6 所示。

图5 3 层BP 网络的训练Fig.5 Three-layer BP network training

图6 预测模型网络结构Fig.6 BP neural network structure

遗传算法参数对遗传算法的运算精度有着重要影响，算法参数主要包括编码长度、适应度函数选择、选择操作、交叉操作、变异方法、种群数目、最大进化次数选取等，具体选择如下所示：

（1）编码长度确定。采用浮点数编码，个体长度即染色体长度计算公式如式（3）所示。经过计算本文S=3×5+5×+5+1=26。

（2）适应度函数选择。为使预测值和实际值之间的残差尽可能小，选择预测样本的预测值和实际值之间的绝对误差之和作为目标函数的输出。适应度函数使用式（4）进行计算。

（3）选择操作。采用随机遍历抽样作为选择算子。并采用轮盘赌法选择竞争成功的个体。

（4）交叉操作。采用单点交叉作为交叉算子。在个体代码串中，仅随机选择一个交点，并且在该点交换两对个体的编码部分。

（5）变异操作。使用变异公式对基因进行变异[10]。

（6）种群数目选取。种群规模越大，代表可同时处理更多数据。一般来说，种群数目取20～100 之间。本文经多次试验，种群数目取60。

（7）最大进化次数选取。最大进化代数作为一种模拟终止条件，一般视具体问题而定。本文中的最大进化次数取100。

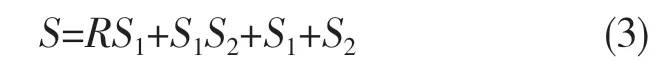
式中：S——染色体长度；R——输入层神经元个数；S1——隐含层神经元个数；S2——输出层神经元个数。

式中：F ——适应度函数；n ——网络输出节点数；yi——BP 神经网络中第i 个节点的实际结果；y'i——第i 个节点的预测结果。

3.2 BPNN 与GA-BPNN 训练结果

BP 神经网络与GA-BP神经网络模型结构为3-5-1，即3 个输入层神经元，5 个隐含层神经元，1 个输出层神经元。将准备好的100 组数据分别代入准备好的BP神经网络及GA-BP 神经网络程序中，对神经网络进行训练，训练在MATLAB 中实现。

图7 为BPNN 与GABPNN训练过程的性能比较。由图7可见，BPNN 与GABPNN 训练曲线、验证曲线以及测试曲线随着迭代次数的增加而下降，最后成功收敛于预设的均方误差；3 条曲线的走向与变化相似，且遗传神经网络三曲线误差更小。图7 中圆圈位置代表迭代停止，BPNN 在4 次迭代之后收敛结束，GA-BPNN 在8 次迭代后收敛结束。GABPNN 比BPNN的收敛时间长，这是因为遗传算法全局寻优，且本文中预设的种群规模较大，种群进化需要较多的迭代次数。

图8 为神经网络模型在样本训练后的线性回归结果，从图8可以看出，BPNN 的相关系数为R=0.968 63，而GA-BPNN 的相关系数为0.979 10，说明遗传BP 神经网络的回归性能更好，具有更好的泛化能力。

3.3 预测结果分析

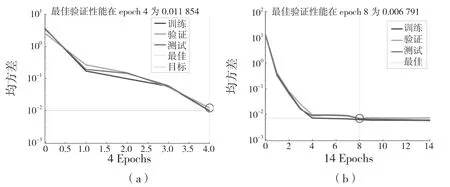
图7 性能验证比较Fig.7 Comparison of training performance of two neural networks

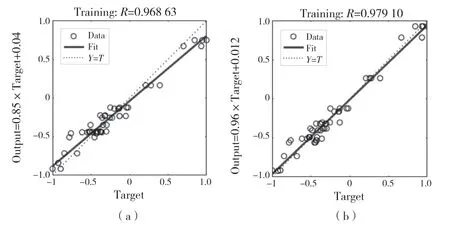
图8 相对系数比较Fig.8 Relative coefficient of two neural networks

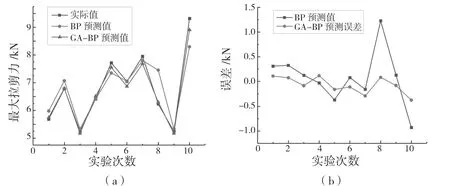
图9 神经网络预测结果及预测误差Fig.9 Neural network prediction result and prediction error

将用于验证的后10 组胶铆接头最大拉剪力数据分别代入训练好的BP 神经网络与GA-BP 神经网络进行预测。实际值与预测结果的比较如图9（a）所示。由图9（a）可知，两者预测输出曲线与期望输出曲线拟合效果较好，基本符合期望输出的变化趋势。由图9（b）可知，BP 神经网络与GA-BP 神经网络误差均在零点附近上下波动，且GA-BP 神经网络波动幅度更小。BP 神经网络预测误差范围在-0.92～1.23 kN，最大相对误差为2.16 kN。而GA-BP 神经网络预测误差范围在-0.37～0.12 kN，最大相对误差为0.49 kN。因此，GA-BP 神经网络的预测精度更高。

对于预测结果，可以通过均方误差（MSE），均方根误差（RMSE）以及平均绝对误差（MAE）这3 个指标来评价。MSE 是实际值与预测值之差的平方的平均值，在线性回归法中为损失函数；RMSE 是衡量观测值与真实值之间的偏差，为机器学习模型预测结果衡量的标准；MAE 是绝对误差的平均值，可以更好地反映预测值误差的实际情况。

具体计算公式如下：