导向臂空气悬架结构有限元仿真与试验验证

2021-04-02潘公宇李阿龙王万青曹崇禧

农业装备与车辆工程 2021年3期

潘公宇，李阿龙，王万青，曹崇禧

（1.212013 江苏省镇江市江苏大学汽车与交通工程学院；2.215000 江苏省苏州市方盛车桥（苏州）有限公司）

0 引言

随着人们生活水平的提高，在物质生活得到满足的同时，人们对于精神方面的需求越来越受到重视。车辆的乘坐舒适性受到了许多生产厂家及客户的关注。在国外，大多数商用车及一些高档乘用车均采用了极受欢迎的空气悬架系统；国内对于空气悬架的使用也在逐渐增多，像多数客车及城市公交车已基本采用了这一系统。空气悬架以其质量轻、结构简单、能够根据实时路况进行气囊刚度的适时调节等优点，极大满足了车辆乘坐舒适性的要求。在获得一定乘坐舒适性的同时，车辆悬架结构系统在正常使用期间的强度及其使用寿命也是研究的重点。

在汽车悬架系统的疲劳耐久性方面，学者也进行了相关的研究。文献[1]通过仿真的方法获得了后扭力梁结构的外部载荷，根据准静态应力分析法及相应的累积损伤准则，利用疲劳软件计算得到了后悬架扭力梁结构的疲劳寿命，通过分析得到了后扭力梁结构产生疲劳失效的原因，但缺少疲劳试验验证仿真计算分析的准确性；文献[2]提出了载荷测试信号分析处理过程，确定低通滤波频率分别为40 Hz和15 Hz，通过频谱分析，得出载荷信号频域能量主要集中在15 Hz，频谱分析结果符合车体结构频率范围；文献[3]基于多轴高周疲劳临界平面损伤参数，即等效应力功率谱密度（PSD），提出了一种多轴随机振动疲劳损伤参数。基于等效应力PSD，结合单轴随机载荷谱法，可以进行多轴随机载荷下的疲劳寿命计算；在文献[4-6]中，相关学者研究了控制臂及其摆臂发生疲劳失效的原因，分析得到疲劳失效多是从焊接位置附近开始萌生，基于此，对焊接质量、材料等进行深入分析。

目前，在许多文献中，学者仅对悬架系统中某一具体结构进行研究，如双横臂悬架的上下横臂、转向节等。鉴于前人对空气悬架系统及疲劳试验的研究较少，本文以某企业开发的一款商用车后导向臂空气悬架系统为研究对象，对组成该悬架的金属结构件进行分析并提出以一种近似等效随机载荷的试验加载方式进行悬架结构台架试验验证；通过在ADAMS/Car 中进行动力学仿真并与有限元仿真分析相结合，得到对悬架系统的随机输入载荷谱以及通过静力分析在3 种极限工况下校核悬架是否存在明显应力集中现象；通过采用线性累积损伤疲劳准则理论，借助N-Code DesignLife 软件进行随机载荷下疲劳寿命的分析计算来预测结构系统在随机载荷下的寿命及损伤值；通过在企业疲劳试验机上进行疲劳试验，对比验证仿真结果的正确性，进一步改善以往疲劳寿命预测分析只进行仿真而缺乏试验验证研究的不足，对预测车辆悬架结构件安全寿命具有重要的现实意义，同时，为企业产品的推广应用及类似产品的开发与验证提供了方法与思路。

1 悬架建模及动力学仿真

空气悬架作为汽车行驶系统中重要的承载部件，与传统的悬架结构相比有独特的优势，空气弹簧取代以往各种形式的弹簧结构减轻了总体质量，并提高了乘坐舒适性。通过与车架、车桥及相关结构相连接来承载地面作用在后轴的各个方向的载荷及车身所传递的载荷。本文所研究的某商用车导向臂空气悬架系统主要由减震器、空气弹簧总成、减震器上支架、减震器下支架、空气弹簧上下安装支架、下横梁、导向臂、衬套及导向臂安装支架等结构组成。根据企业提供的空气悬架设计尺寸，采用专业的三维实体建模软件UG 画出总体结构图。按照工程分析中的等效原则，将所受载荷施加于轮心处进行有限元静强度分析校核，故将驱动桥桥壳加入分析模型，如图1 所示。

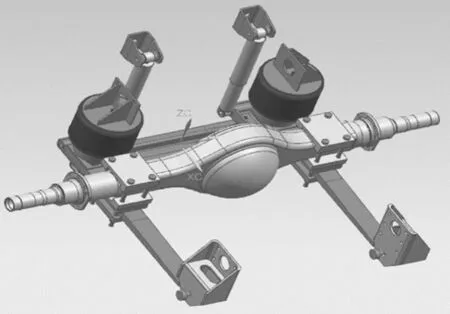
图1 系统CAD 模型Fig.1 CAD model of system

在ADAMS 软件中建立导向臂后悬架动力学分析模型。首先，在ADAMS/Car 中建立后悬架、副车架、减振器、车桥、轮胎等子系统并将子系统组装成所需模型，然后确定模型各参数，如悬架质量、弹簧刚度以及衬套的各向刚度等。建立的动力学仿真模型如图2 所示。

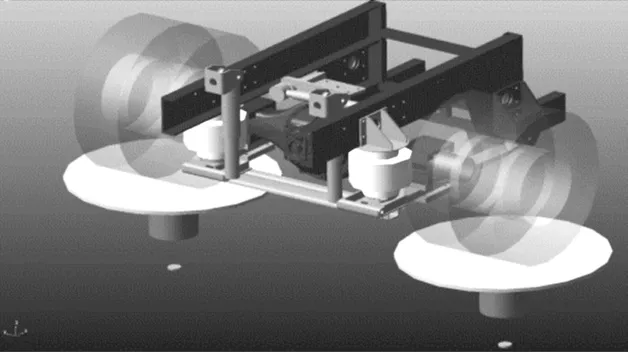
图2 动力学仿真模型Fig.2 Dynamic simulation model

为了对悬架进行静强度的校核及疲劳寿命的预测，必须得到所需要的输入条件，由于所涉及车辆行驶的路况较好，故采用B 级路面的输入作为路面激励。采用滤波白噪声建立路面输入时域模型作为动力学仿真的路面输入激励。在动力学仿真软件ADAMS 中仿真得到给定路面下轮心处所受到的随机载荷分布及在特定工况下的最大载荷，从而对该模型进行结构强度校核与疲劳寿命的预测分析[7]：

式中：G（qn0）——路面不平度系数，m3；n0，f0——参考空间频率与路面空间截止频率，n0=0.1 m-1，f0=0.062 8 Hz。

在MATLAB Simulink 环境下，搭建与式（1）相一致的仿真分析模型，如图3 所示。

在B 级路面，以车速为30 km/h 工况下进行路面不平度输入仿真分析作为动力学仿真模块的路面输入[8]，设定好相关参数，通过动力学仿真分析得到在该路面输入下的载荷时间历程曲线，如图4 所示；并且，在3 种特定工况下进行仿真，得到在给定工况下的最大载荷。

图3 路面不平度时域仿真模型Fig.3 Road surface roughness time domain simulation model

图4 路面载荷时间历程曲线Fig.4 Road load time history curve

2 悬架结构有限元仿真分析

在汽车产品的开发与设计过程中，有限元分析方法起到了极其重要的作用，尤其应用于求解复杂的物理数学问题以及处理工程中的实际问题。通过有限元软件对所研究结构的离散化处理，运用计算机的快速计算求解得到结构的平衡方程结果。获取结构在边界条件及各约束下的响应来评价所设计的产品的合格与否，对产品的开发及优化具有指导意义[9]。

由于主要研究对象是悬架结构的金属构件部分，在静力学分析时，对悬架结构件受力特点进行适当的简化，简化后的模型如图5 所示。

图5 系统简化后CAD 模型Fig.5 CAD model after system simplification

2.1 有限元分析

根据已有的悬架结构模型，能够较为容易地对目标结构进行有限元建模，将简化后的实体模型导入到专业的划分网格软件中，分别对悬架结构与驱动桥桥壳进行有限元网格划分。将结构部件的三维实体模型导入到HyperMesh 模块中对其进行实体网格划分，得到有限元网格模型。考虑到结构比较规则易于生成质量较好的网格，因此，在网格的选择上，主要通过Solid map 命令进行六面体网格的生成。划分的网格如图6 所示，共得到233 053 个网格单元，81 773 个节点。划分完网格后，对网格进行单元质量的检查，并将各组件单元及材料属性赋予相对应的网格。该悬架结构部件材料分别采用Q345 普通碳素结构钢、用于导向臂结构的弹簧钢50CrVa，45 钢及所用衬套的各向刚度。另外，桥壳材料采用510L。各部件所对应的的材料参数如表1 所示。

图6 有限元实体模型Fig.6 Finite element entity model

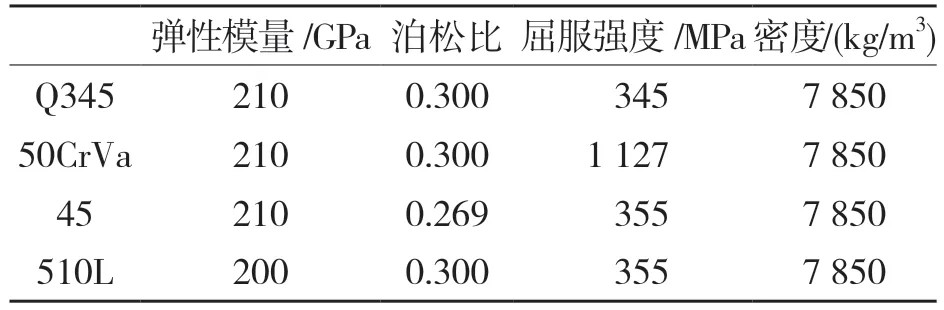
表1 材料参数属性Tab.1 Material parameter properties

另外，在校核悬架结构的静强度之前，对导向臂衬套部分进行6 个方向上的静态刚度分析。将衬套中心点各向自由度设为固定，并赋予衬套外侧节点的缩径量 0.8 mm，以模拟实际安装情况。在3 个轴向依次释放相应的自由度，并沿该方向给予3 mm 的位移量，再绕轴向方向依次给予10°的转动量，仿真结果如图7 所示。

图7 衬套六向刚度曲线Fig.7 Six-way stiffness curve of bushing

由图7 可知衬套在X，Y，Z 向及绕 X，Y，Z 向扭转刚度，其大小如表2 所示。

表2 衬套各向静刚度值Tab.2 Static stiffness value of bush in all directions

2.2 工况分析

在对悬架的强度校核分析中，常常将汽车结构在实际行驶过程中处在极限工况下的状况进行分析，因此，分别选择在急加速工况、受最大侧向力工况及受到冲击载荷3 种极限工况下，对悬架结构件进行强度校核。基于在ADAMS 中的仿真，得到静态下3 种极限工况的载荷输入条件如图8 所示。

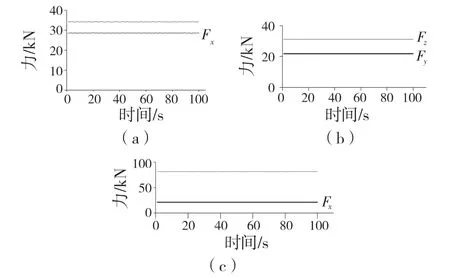
图8 3 种极限工况下的最大载荷Fig.8 Maximum load under three extreme conditions

2.2.1 急加速工况

汽车起步后，经驾驶员加速达到某一速度时，分析计算在该过程中车辆悬架所受到的最大载荷情况，校核在这一工况下，悬架在受力作用后是否存在应力集中现象，以判断是否满足设计要求。

在此工况下，突然加速会使车辆产生轴荷转移现象，会使后轮的载荷变大，汽车后悬架主要受到车辆纵向平面内的推力和横向平面内的车轮作用于悬架的力。因此，悬架受到2 个方向的合力。在ANSYS-Workbench 中施加载荷及约束，其中，载荷施加于轮心处，沿2 个方向分别输入上述载荷，将悬架与车架相连的部件进行全约束，约束结构在6 个方向上的自由度。求解后应力结果如图9 所示。

2.2.2 最大侧向力工况

汽车在转向时，在离心力的作用下，会朝着与转弯方向相反的方向发生侧倾，致使悬架在车身侧倾的一侧受到的载荷变大，对结构的破坏比较大，因此，需要校核在这一工况下结构的强度是否满足使用的要求。由于车辆的侧倾现象，侧倾一侧轮心受力为重点考虑对象，同时，忽略前进方向所受到的力。按上述加载方式在ANSYSWorkbench 中施加载荷及约束，求解后应力结果如图10 所示。

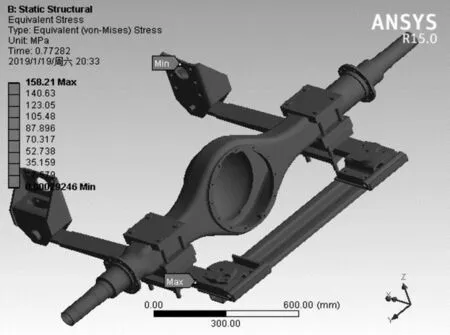
图9 急加速工况下应力云图Fig.9 Stress cloud diagram under rapid acceleration

图10 最大侧向力工况应力云图Fig.10 Maximum lateral force condition stress cloud

2.2.3 冲击载荷工况

汽车在通过凸起的减速带或凹坑的路面时，会受到作用于车辆的冲击载荷的影响，因此在垂向平面内，此工况会对车辆悬架结构产生相应的影响。需校核在受到冲击载荷时所研究的悬架结构是否满足设计的要求。此工况下，按照规定的标准给予垂向受力的动载荷系数为2.5。求解结果如图11 所示。

图11 冲击载荷工况下应力云图Fig.11 Stress cloud diagram under impact load conditions

综上分析可知，3 种工况下悬架结构的应力均未达到材料的强度极限，受到的最大应力均出现在导向臂与减震器下支架之间，说明在悬架的结构中该处是容易出现应力较为集中的部位，后期可以考虑对其进行优化分析。受到的最大应力在极限范围内，因此一般情况下该结构部件不会发生脆性断裂，为确保满足设计使用要求，在此基础上对该结构进行疲劳研究尤为重要。

3 疲劳寿命预测

汽车行驶过程中，悬架承载构件受到随时间变化的随机载荷作用而产生动态循环应力，在高应力区会引发疲劳损伤。疲劳是应力或应变的波动所引起的，这些波动被称为循环，应用雨流循环计数法可从时间关系曲线中获取循环中的应力幅值与均值。在满足强度需求的基础上，为进一步确定车辆悬架部件在运行期间的安全性，疲劳寿命的分析研究尤为重要。

由于车辆在实际运行情况下载荷的随机性，为便于分析，需要对载荷时间历程进行处理。实际载荷谱包括大量数据，通过雨流循环计数法能够将一系列不规则的随机载荷转换成各种不同幅值下的循环数，并利用获得的峰值及谷值求出载荷的幅值和均值，最终构成计算所需要的雨流矩阵[10]。基于静力分析结果，在3 种极限工况下，应力值均小于材料的屈服极限，故悬架结构的破坏落在了高周疲劳的范畴，从而考虑运用应力疲劳强度分析方法对悬架结构进行疲劳寿命的分析预测。根据材料库中相应材料的S-N 曲线及疲劳损伤累积理论，在N-Code DesignLife 中对悬架结构的疲劳寿命进行解算，得到相应的疲劳寿命及损伤云图如图12 所示。

分析表明，悬架结构在受到随机载荷条件下的最小寿命为4.151E7 次，达到了普遍公认的最小疲劳寿命106次级的要求，符合企业产品质量设计要求。并找到了容易受到破坏的位置区域，对所开发悬架结构作进一步优化提供参考。

4 疲劳试验分析验证

为验证疲劳预测的准确性与真实性，通过疲劳试验台架对悬架结构进行疲劳耐久性试验验证。按照与前述静力分析相同的方式，从底部轮心部位对悬架进行载荷的施加，将悬架及驱动桥用螺栓按照汽车实际装车状态相连接，倒放在试验台架上，将其与车架相连接的部位用螺栓与试验台架底部固定以模拟在实际过程中与车架间连接的情况。

图12 随机载荷下悬架疲劳寿命及损伤云图Fig.12 Suspension fatigue life and damage cloud map under random load

在测试之前，将悬架结构安装在台架测试台上，参照上述分析，在悬架导向臂应力集中部位粘贴应变片，分别在悬架两侧导向臂处、气囊下支架、导向臂安装支架各粘贴1 个应变片，用测定计、应变仪及光线示波器进行检测[11]。液压油缸作为力输入部件，提供试验所需的力，力的大小由力传感器反馈。由控制器直观显示和控制力的值，如图13 所示。另外，为保护油缸，在气缸的每个端部处存在球铰接头，确保油缸仅受到轴向力的作用。

图13 悬挂试验台监控系统Fig.13 Suspension test bed monitoring system

轮心两侧的液压伺服作动器固定在龙门架上作为施力装置。试验时，为尽可能贴近仿真得到的随机载荷，采用了与前人不同的载荷作用方式。在载荷幅值范围内从最小值增加到最大值的区间内取一组值来近似模拟在实际过程中所受到的力，通过对数据进行相应拟合，近似构成三角波的形式，以该方式输入台架试验控制台，从而作用于2 个液压机构。试验过程中，考虑到现有设备功能有限，无法实现高频加载，在此不考虑载荷频率对台架试验的影响。通过在悬挂试验台监控系统中进行参数设置，两侧液压作动装置分别设定为幅值范围内的载荷值，通过时间的迟滞性交替作用到车桥上，以此将受到的力在悬架系统中进行传递。为增强试验说服力，避免因巧合或人为安装方式对实验结果的影响，试验选择专业人员进行安装及加载，具体安装及实施方式如图14 所示。