顾及气候差异的区域加权平均温度模型——以中国陕西为例

朱 海，黄观文，张菊清

长安大学地质工程与测绘学院，陕西 西安 710054

天顶对流层延迟(zenith tropospheric delay,ZTD)是大气的一个重要参数。GNSS技术可以获取精确的ZTD、站点坐标等信息，具有时间分辨率高、站点分布广泛、精度高、不需要对仪器进行定标等特点，目前已广泛应用于灾害监测、反演大气可降水量等方面的研究。

Tm为加权平均温度，是测站天顶湿延迟(zenith wet delay)在转换可降水量(precipitable water vapor,PWV)时，水汽转换因子Π中唯一的变量。Tm的精度对PWV的精确确定起着极其重要的作用。但是，我国幅员辽阔，地形起伏较大，使得实际的大气湿廓线变化复杂，难以在大范围建立高精度的Tm模型。因此，国内外学者针对Tm模型展开了一系列的研究。文献[1]根据计算13个美国(27°N—65°N)范围内8718次的探空站资料，得出Tm和Ts的一元线性表达(Tm=0.72Ts+70.2)，首次将加权平均温度与地表温度联系了起来。该模型简单，实用，但难以保证在其他区域获取高精度Tm估计值。文献[2]使用2001年—2010年10年的ERA-Interim数据，改进并合并了GPT(global pressure and temperature)和GMF(global mapping function)，建立了新的全球GPT2模型。文献[3]改进了GPT2模型，在该模型基础上将格网分辨率提高至1°，并添加了Tm项。文献[4]基于球谐函数构建了全球大地观测系统的大气数据建立了GTm-Ⅲ(global weighted mean temperature-Ⅲ)，提出了新的近地大气温度全球Tm模型[5]，并且构建了顾及非线性高程归算的Tm模型[6]GTm-H(global weighted mean temperature-height)。文献[7—8]利用ERA5数据构建了新的全球和中国地区Tm经验模型。文献[9]针对中国区域起伏较大的特点，构建了估计季节精细变化的Tm垂直递减率函数模型。以上研究均对Tm模型提出了建设性的意见，将依赖地面气象资料的难度降低，只需要地理和天文资料。但这样势必会牺牲与实时气象信息的联系，精度也会因此受损。针对区域化的Tm模型，还有很多专家学者也提出了有建设性的意见。一些学者基于探空资料，采用多元线性回归分析的方法分别得到了湖南[10-11]、长三角[12]、贵州[13]、新疆[14]等地区的Tm的区域模型。以上研究拓展了Tm的多因子模型，提高了Tm回归模型的精度，但存在探空站分布不均，导致回归分析误差较大，且未考虑季节周期误差对模型的影响。文献[15]对中国区域Tm分气候区进行回归分析发现，Tm-Ts模型中a、b系数与气候相关关系明显，但未就其原因给出进一步讨论。

本文针对目前主流Tm模型所存在的问题，建立了一种与气象信息紧密联系，顾及周期改正和气候差异的区域Tm模型，将季节周期改正加入到传统回归模型中。陕西省是中国气象灾害最频繁的地区之一，夏季气象易变，加上黄土高原土质松软的地质特征，遇暴雨天气极容易发生泥石流、山体滑坡等地质灾害。此外，陕西省相较其他地区地形起伏较大，气候类型相较其他区域更复杂，对模型适用性的要求更高。陕西省已有大量的地基GNSS站，但目前极少用于高精度可降水量观测，缺乏气象应用[16-19]。因此，对陕西省进行高精度大气可降水量的观测对于天气预报、防灾减灾，保障人民财产安全具有极其重要的意义。

1 数据及处理方法

1.1 ECMWF格网数据

由于陕西省探空站分布过于稀疏，而根据已有的探空站得出的Tm预测公式难以在陕西省全域实现高精度Tm的解算。因此，本文提出利用ECMWF提供的2016—2018年空间分辨率0.5°×0.5°，时间分辨率6 h一次的气压分层数据，垂直分辨率为37层，每层气象数据有温度T(K)、位势Z(m2/s2)、比湿q(kg/kg)、气压P(hPa)和对应时段的表面数据：“2 m温度(2 meter temperature)”、“表面压力(surface pressure)”(pa)结合SRTM(shuttle radar topography mission)提供的高分辨率、高精度的数字高程模型(digital elevation model,DEM)计算陕西省所有研究格网点上的Tm弥补了探空站空间分辨率的不足。

Tm的计算利用数值积分法，将水汽压e和温度T沿着测站或格网点上空天顶方向进行积分

(1)

Tm=Tm0+β(h-h0)

(2)

式中，T为绝对温度(单位为K)；β为温度衰减率；h0和Tm0为参考点的高度和Tm；h-h0范围为整个对流层；Z为沿天顶方向高度(单位为km)；水汽压e(单位为hPa)无法通过实测获得，需要利用式(3)计算

e=q×P/0.622

(3)

式中，q为比湿；P为大气压(单位为hPa)。

1.2 无线电探空数据

本文利用美国怀俄明大学提供的陕西境内Yanan(36.6°N,109.5°E)，Jinghe(34.43°N,108.97°E)，Hanzhong(33.06°N,107.03°E)3个无线电探空站数据资料研究陕西省3个探空站点的Tm，并对ECMWF数据计算的结果进行验证。同样利用数值积分法(式(3))计算Tm，水汽压e通过露点温度Td和饱和水汽压es公式间接计算[7]

(4)

水汽压e的计算公式如下

(5)

式中

(6)

1.3 高程转换

气象数据在记录的时候，通常是对不同等压面进行记录。数值气象资料用位势Z(m2/s2)记录，无线电探空数据用位势高记录，GNSS站点与DEM高程往往采用WGS-84坐标系。因此，在高程转换方面需要将其位势高转为大地高，步骤如下：

1.3.1 计算位势高度

h位势=Z/g

(7)

式中，g为重力加速度。

1.3.2 位势高转换为正高

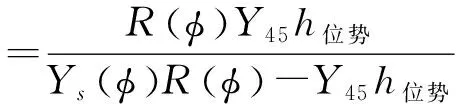
(8)

式中，R(φ)为地球有效曲率半径；Ys(φ)表示旋转椭球正常重力值；Y45为标准重力加速度(Y45=9.806 65 m/s2)，即在纬度φ为45°时，海平面位置的重力加速度。R(φ)、Ys(φ)可由式(9)和式(10)获得

(9)

(10)

1.3.3 正高转换为大地高

h=h正+η

(11)

式中，η表示高程异常，利用美国国家地理空间情报局发布的EGM2008(earth gravitational model 2008)提供的高程异常信息进行改正[20]。

1.4 研究区域

选取包含整个陕西省的北纬40°N—31°N，东经105°E—111.5°E作为研究区域。选取19个均匀且覆盖整个陕西省的格网点，以及陕西境内3个探空站Yanan(36.6°N,109.5°E)，Jinghe(34.43°N,108.97°E)，Hanzhong(33.06°N,107.03°E)构建区域化回归模型。具体分布如图1所示。

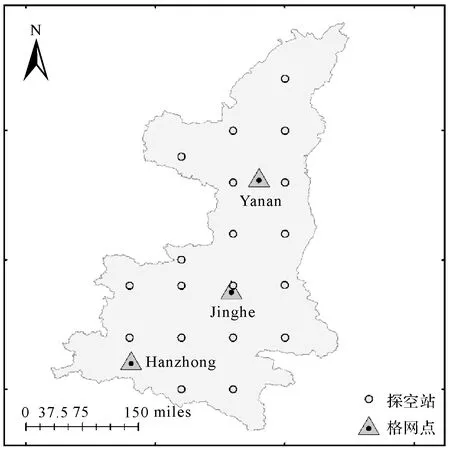
图1 研究区域内选取格网点及探空站分布Fig.1 Various network points and sounding stations in the study area

2 陕西省Tm区域化模型建立

2.1 相关影响因子分析

在此研究之前，众多专家学者已得出Tm与地表温度Ts、露点温度Td、地表气压P、地表水汽压es等均呈良好的相关性，如图2(a)、(b)。除此之外，文献[21]推导出Tm与地表温度Ts存在非线性函数关系，突破了传统的Tm与地表温度Ts近似为一次函数关系的认识。但因为陕西省内并无较高海拔的地区，非线性模型增加了模型复杂程度，相较于线性模型精度却没有明显提高。在实际应用中，采用线性模型来描述陕西省Tm和地表气象因子的关系更加切合。还有专家学者提出了其他影响因素，文献[22]探讨了温度递减率对Tm的影响;文献[23]认为对流层顶的变化趋势对Tm存在一定程度的影响;文献[24]考虑了地形起伏对水汽转换因子的影响等；文献[25]对Tm回归公式进行了验证和分析。以上众多专家均得到了诸多有价值的结论。在本文中，考虑到陕西省地形起伏，南北温差较大，因此选择与Tm相关性较好的Ts与P，探讨与Tm之间的关系。

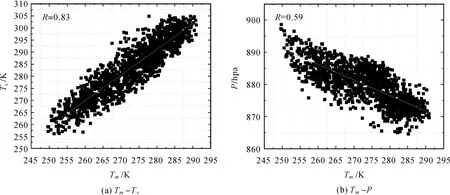
图2 Tm与相关气象因子关系图Fig.2 The relationship between Tm and related meteorological factors

2.2 陕西省多气象因子Tm区域化模型建立

利用ECMWF提供的2016—2018年再分析数据结合3个探空站数据进行建模，考虑到选择较多的气象因子加入模型对精度并没有提高，而且增加了模型复杂程度以及实际应用的局限性。因此本文选择与Tm相关程度较高的地表温度Ts，地表压强P两个气象因子，对陕西省所有研究格网点和探空站的数据进行多元线性回归分析。

设多元线性方程

Tm=aTs+bP+c

(12)

则其误差方程为

(13)

根据最小二乘原理

VTPV=min

(14)

得到不同气象因子的陕西省整体的回归模型如表1所示。

表1 陕西省Tm区域化模型

2.3 陕西省单因子Tm区域化模型精化

从上述研究发现，多因子模型可以提升区域建模的精度，但效果并不显著。同时，增加气象因子意味着加大实际获取气象数据的难度。需针对单气象因子模型进行了季节周期性改正的研究。改进的单因子Tm模型表达式如下

(15)

Tm与Ts相关性是众所周知的

(16)

式中，Tm与Ts之间存在较强的相关性，且两者均呈现出随季节变化周期性，见图3(a)、(b)。

所以，在传统回归模型中，由于Tm与Ts均呈现出随季节变化周期性，因此线性公式平滑了大部分周期。但依旧存在着一部分周期导致的误差并未被消除，模型残差中依旧存在比较明显的周期项，如图4所示。

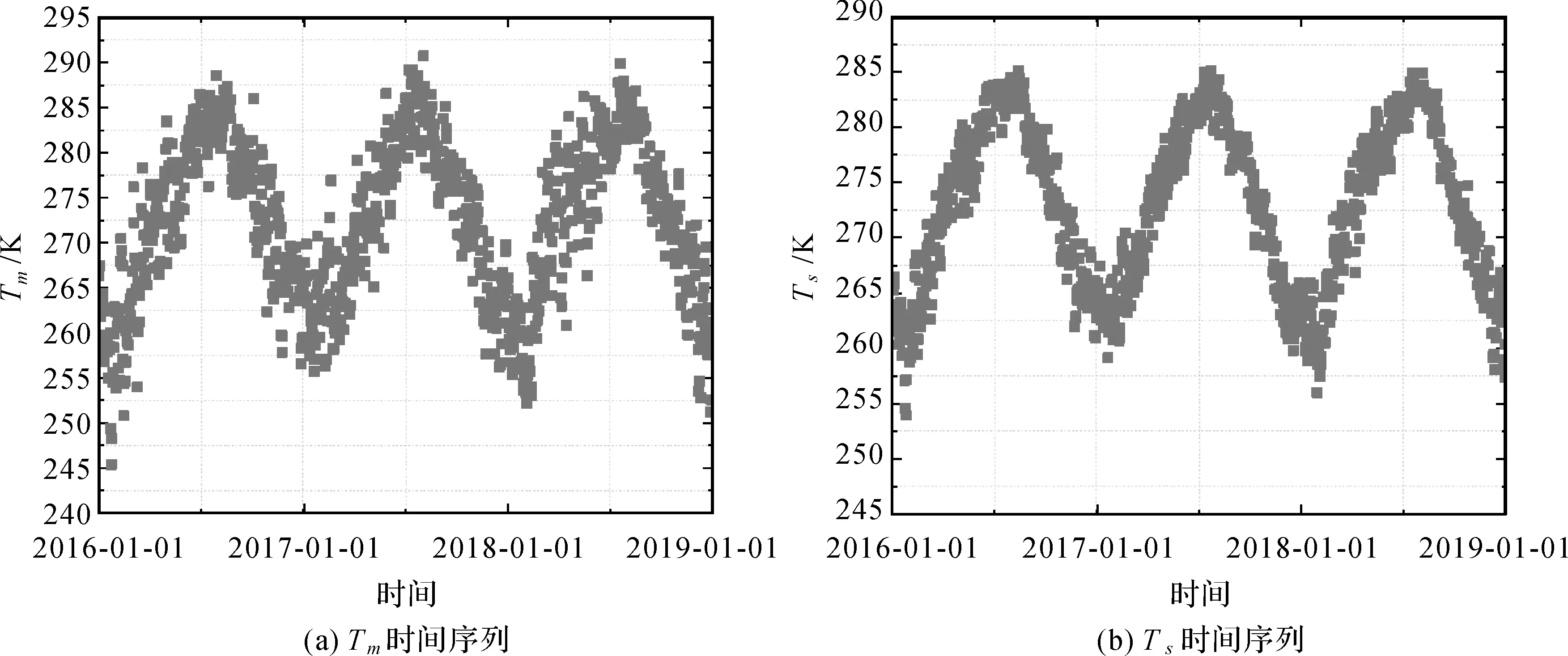
图3 Tm-Ts时间序列图Fig.3 Time series graph

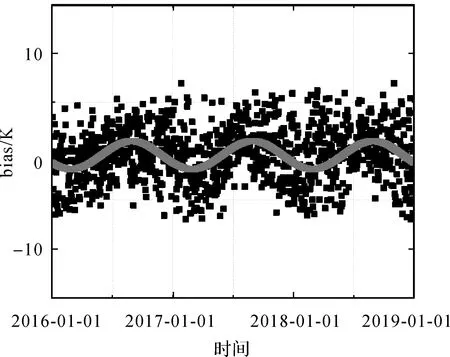
图4 Tm-Ts模型残差时间序列图Fig.4 Model residuals time series graph

Tm-Ts模型的bias随年积日变化呈现出季节特征，这部分未被消除的周期误差对模型精度影响较大。本文参考GPT2w[3]采用的顾及年周期和半年周期的三角函数表达式反映Tm的季节变化。在本文中也使用该函数对模型进行修正，以消除模型中仍旧存在的周期性误差。表达式如下

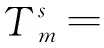
(17)

式中，DOY为年积日；β1、β2为年周期振幅；β3、β4为半年周期振幅；α1、α2、β5均为常数。

因此，本文利用均匀覆盖陕西省的19个格网点结合3个探空站的2016—2018年数据根据最小二乘原理建立了顾及周期性改正的陕西省Tm区域化模型如下

(18)

2.4 顾及气候差异的Tm区域化模型

由于回归分析的方法要求研究区域的范围不能过大，否则精度将不能得到保证。而陕西省与其他省份不同，有着极大的自然地域差异。陕西省被北山和秦岭划分为三大自然区：北部为陕北黄土高原、中部为关中平原、南部为陕南秦巴山区。复杂多样的地形地貌以及海拔高度(图5(b))也决定了陕西多样的气候特征：陕北大部地处海拔较高的黄土高原，属于中温带季风气候、关中为一马平川的平原，暖温带季风气候、陕南处山峦纵横的秦巴山区，属于北亚热带季风气候。其气候特征差异较大，而回归模型适合气候类型简单的区域，否则会影响模型精度。因为其自身局限性，使用一种回归模型在如此复杂多变的气候环境中是不合适的。因此，本文在建模时考虑了陕西省复杂的气候类型对Tm的影响。

本文以北山-秦岭为分界线将陕西省划分为3个气候区，北部为以黄土高原为主的中温带季风气候区，中部为以关中渭河平原为主的暖温带季风气候区，南部为以秦巴山区为主的北亚热带季风气候区。如图5(a)所示。

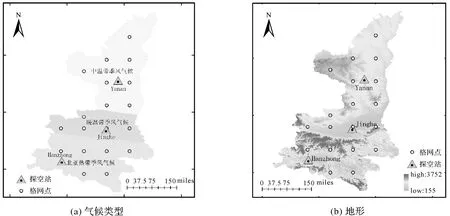
图5 陕西省气候类型及其高程信息(DEM)Fig.5 Climate types and digital elevation model (DEM) in Shaanxi

气候类型对Tm有着很大的影响，文献[15]对中国区域Tm分气候区进行回归分析发现，Tm-Ts模型a、b系数与气候相关关系明显，因此在不同气候类型的区域分类进行建模对于提升模型精度有显著的作用。本文对处于不同气候区格网点与探空站的数据进行回归分析，得到不同气候区顾及年周期单因子区域模型(表2)。

表2 陕西省不同气候区回归模型

通过对比，不同气候类型地区模型有所差异。这是由于中温带季风气候区(陕北地区)属半干旱区，大部地处黄土高原，气候特点为春季气温回升相对较快，干燥且温暖；夏季日照时间充足，大部较为炎热；秋季温度下降较快，凉爽且干燥；冬季寒冷干燥，气温较低。一年四季干旱少雨，日夜温差较大，因此Ts与Tm的相关性相对其他气候区较低。北亚热带季风气候区(陕南地区)属湿润区，温度适中。而暖温带季风气候区(关中地区)则属半湿润区，中和了前两者的特征，四季分明，从模型系数可以很好地看出其不同气候特征的表现以及过渡。

由陕西省整体DEM(图5(b))看出，不同气候区选取的格网点以及探空站纬度，格网点高程差异较大。说明这些点所处的不同气候区有着极大的气候差异，这也说明在陕西省顾及气候差异的建模方法更为合理，可靠。

为了降低实际工程应用中使用该模型的局限性，本文根据建模所利用的探空站以及格网点的空间分布提出应用于陕西省的Tm分段函数模型，在实际应用中，可以根据测站纬度来选择要使用的模型。模型表达式如下

(19)

3 模型可靠性验证

本文利用平均偏差(bias)，标准差(STD)和均方根误差(RMS)来评价建模精度。bias表示模型与真值的偏离程度，即模型预测的Tm与探空数据实测得到的Tm之间的偏差v累加的平均值；STD表示误差离散的程度；RMS表示模型的稳定性以及可靠性。

(20)

(21)

(22)

3.1 多气象因子模型可靠性验证

利用未参与建模的2019年1—12月无线电探空数据对计算结果进行验证。选择研究区域内3个探空站Yanan(36.6°N,109.5°E)，Jinghe(34.43°N,108.97°E)，Hanzhong(33.06°N,107.03°E)，分别验证模型bias、RMS和STD。

由表3可以看出，3个探空站数据的RMS变化趋势表现出一致性，双因子模型和单因子模型精度相当，模型STD较稳定且均小于3 K，说明模型可靠性较高。模型整体RMS与STD随纬度上升而降低，处于陕南地区的Hanzhong(33.06°N,107.03°E)RMS范围在2.12～2.90 K，多因子建模对精度提升较高；陕北地区的Yanan(36.6°N,109.5°E)RMS范围在2.81～3.03 K，增加的多气象因子并无带来明显的精度提升。

陕北地区大部地处黄土高原，属半干旱区，纬度以及海拔相对其他研究区域较高，Ts、P变化幅度较大，Ts与Tm的相关性相对于其他研究区域较高。研究区域内随纬度变化体现出较大的气候差别，因此，分气候区对研究区域进行建模对提高模型精度是必要的。陕西省处于中低纬度地区，将单因子模型与Bevis模型进行比较可以间接说明建模合理性(图6)。

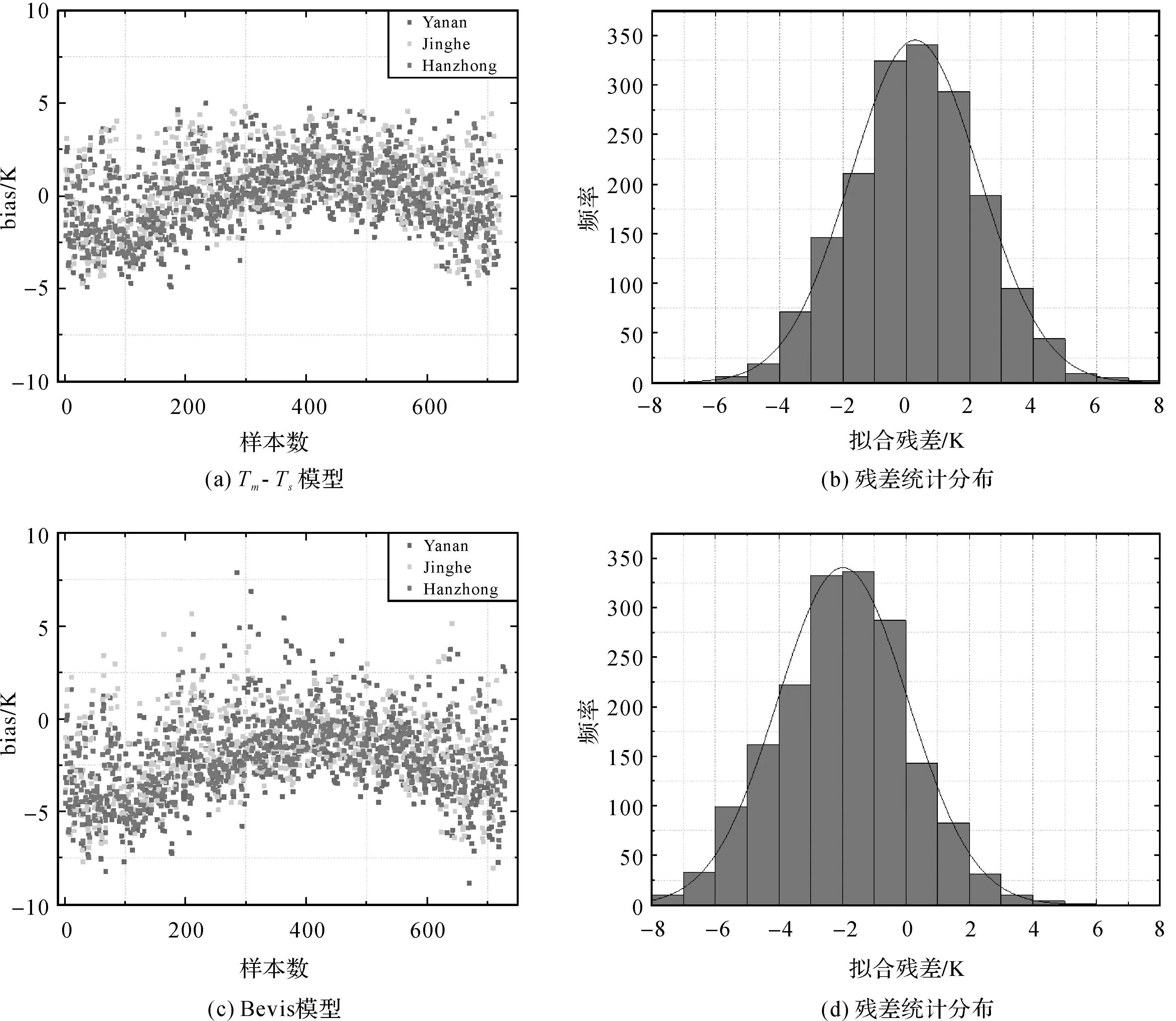
图6 区域化Tm-Ts模型残差与Bevis模型比较Fig.6 The bias of Tm-Ts model comparison with Bevis model

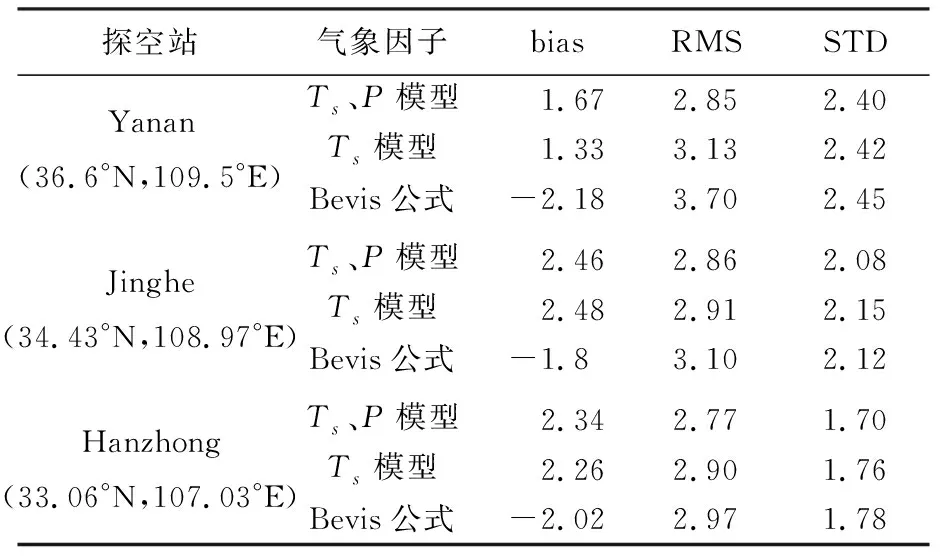
表3 陕西省Tm区域化模型误差分析

Bevis模型是利用中低纬度的无线电探空数据建立的。从表3可以看出，Bevis模型与本文建立的Tm-Ts模型精度变化表现出一致性，整体精度随纬度上升而降低。本文得出的Tm-Ts模型与Bevis模型一次项大致相等，但该Tm-Ts模型相较于Bevis模型在常数项有所修正。与探空数据比较， 精度提升幅度0.07～0.57 K不等，说明本文提出的建模方法是正确以及可靠的。同时，本地化的Tm模型很好地修正了Bevis模型的系统偏差，使得区域化Tm模型准确性更高，更适用于陕西省。

3.2 顾及周期性改正的Tm区域化模型可靠性验证

利用未参与建模的3个无线电探空站2019年1—12月的数据(对一天内两次采样取平均值)评估顾及周期性改正的Tm区域化模型精度，见表4、图7。

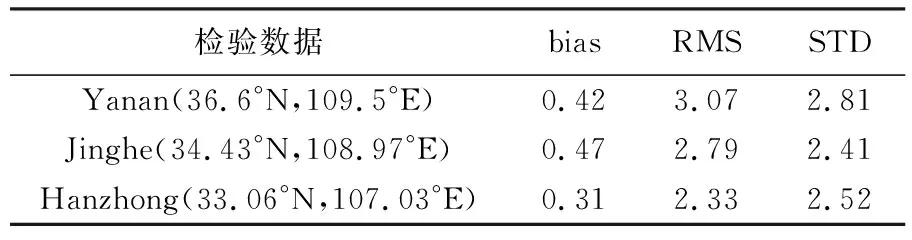
表4 顾及周期性改正Tm区域化模型精度

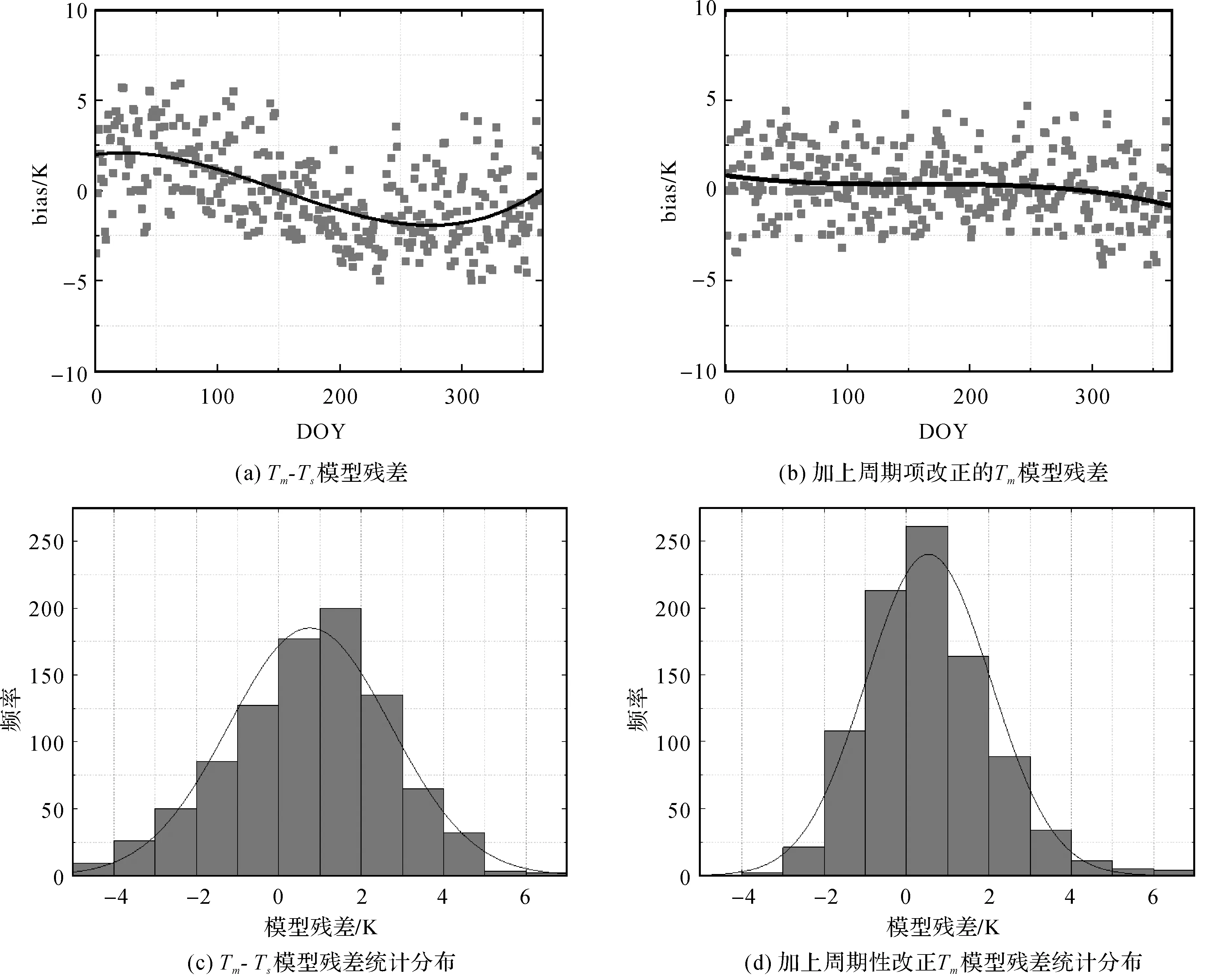
图7 加周期项前后残差变化Fig.7 Residual variation of periodic correction

如图7(b)所示，顾及周期性的陕西省Tm区域化模型虽然同样呈现出一定的周期性，但相比之前明显减小。说明在增加了周期项之后，使得残差的周期特性减弱，残差随高程变化特性降低，模型精度变高。由表4可知，精度分别提升17%、10%和21%，提升幅度较为显著。

3.3 顾及气候差异Tm模型可靠性验证

3.3.1 利用无线电探空数据验证

从表5可以看出，考虑气候差异对Tm进行建模有着明显的优点，利用探空数据验证顾及气候差异的Tm模型，其RMS明显小于整体模型。因为陕西省气候类型复杂，这是其在建立区域化Tm模型需要区别于其他省份的主要特点，同时证明了分气候区建模的必要性(图8)。

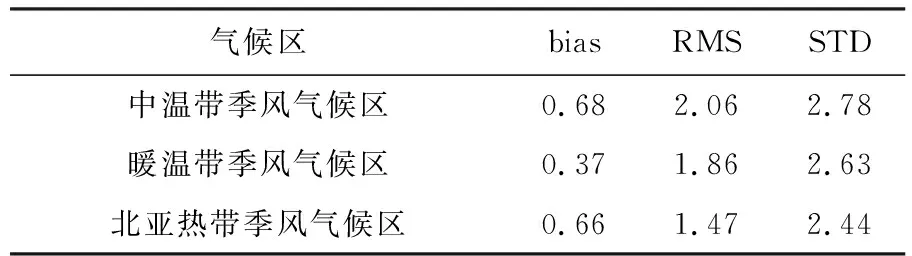
表5 顾及气候差异的Tm模型精度

3.3.2 利用ECMWF数据验证

为了更好地验证顾及气候差异的Tm模型在陕西全域的精度，除验证3个探空站的精度以外，本文利用未参与建模的2019年1—8月ECMWF数据对陕西省所有研究格网点上的气象数据进行了模型精度验证，见表6、图9。

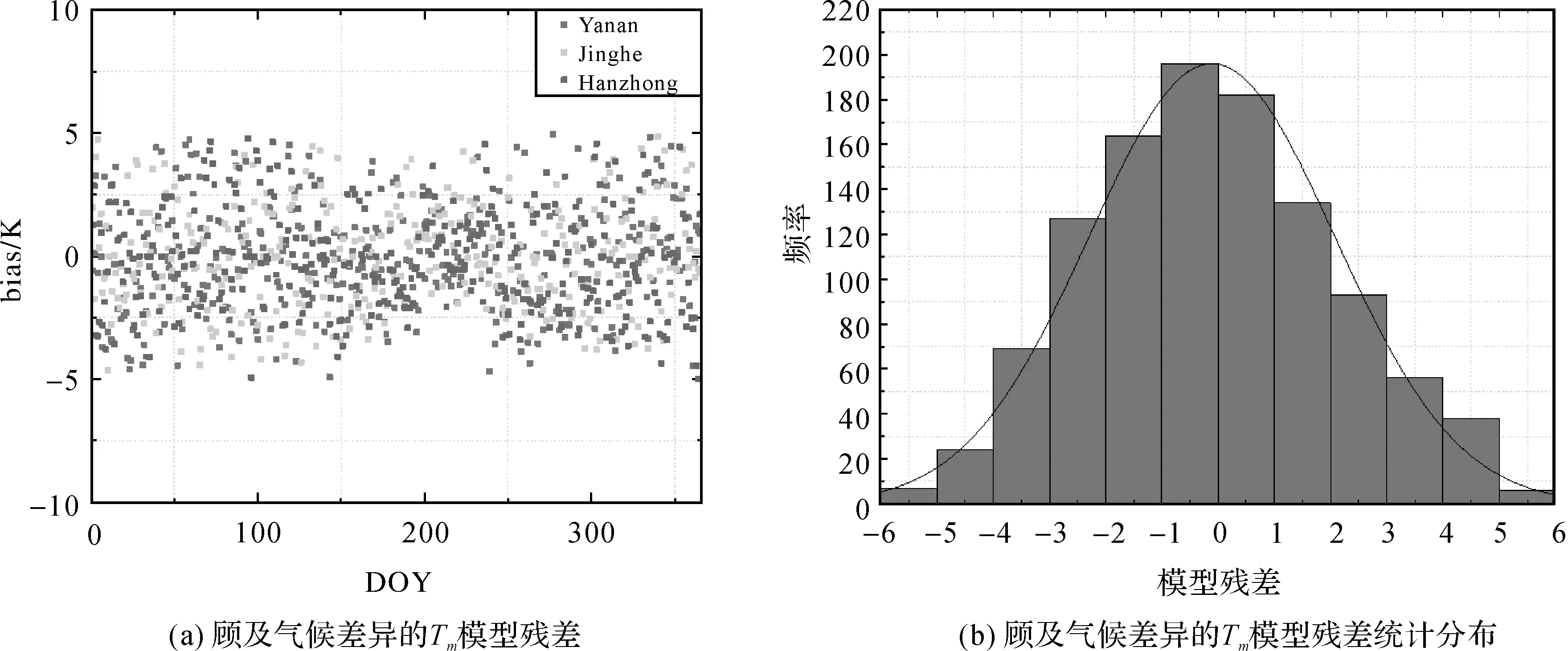
图8 顾及气候差异的Tm模型日均残差变化Fig.8 Daily residual variation of the model

图9 顾及气候差异的模型RMS与STDFig.9 STD and RMS of the model in different climatic regions

从表6可以看出，最大RMS为3.67 K，即对应PWV的误差大约为0.55 mm。考虑区域气候差异可以在不同气候类型的地区有效减小误差，提高模型精度，从图9(a)、(b)可以看出，顾及气候差异的Tm模型在整个陕西省都有很高的精度，在陕西省均可以满足高精度Tm的获取。

3.4 Tm模型综合精度评价比较

为了便于GPS气象学应用，获得最为适合陕西省的Tm模型，本文将所建立的模型与Bevis模型进行统一模型精度评价，结果见表7。在实际工程应用中，可以根据实际情况选择合适的模型。

表6 顾及气候差异的Tm模型精度

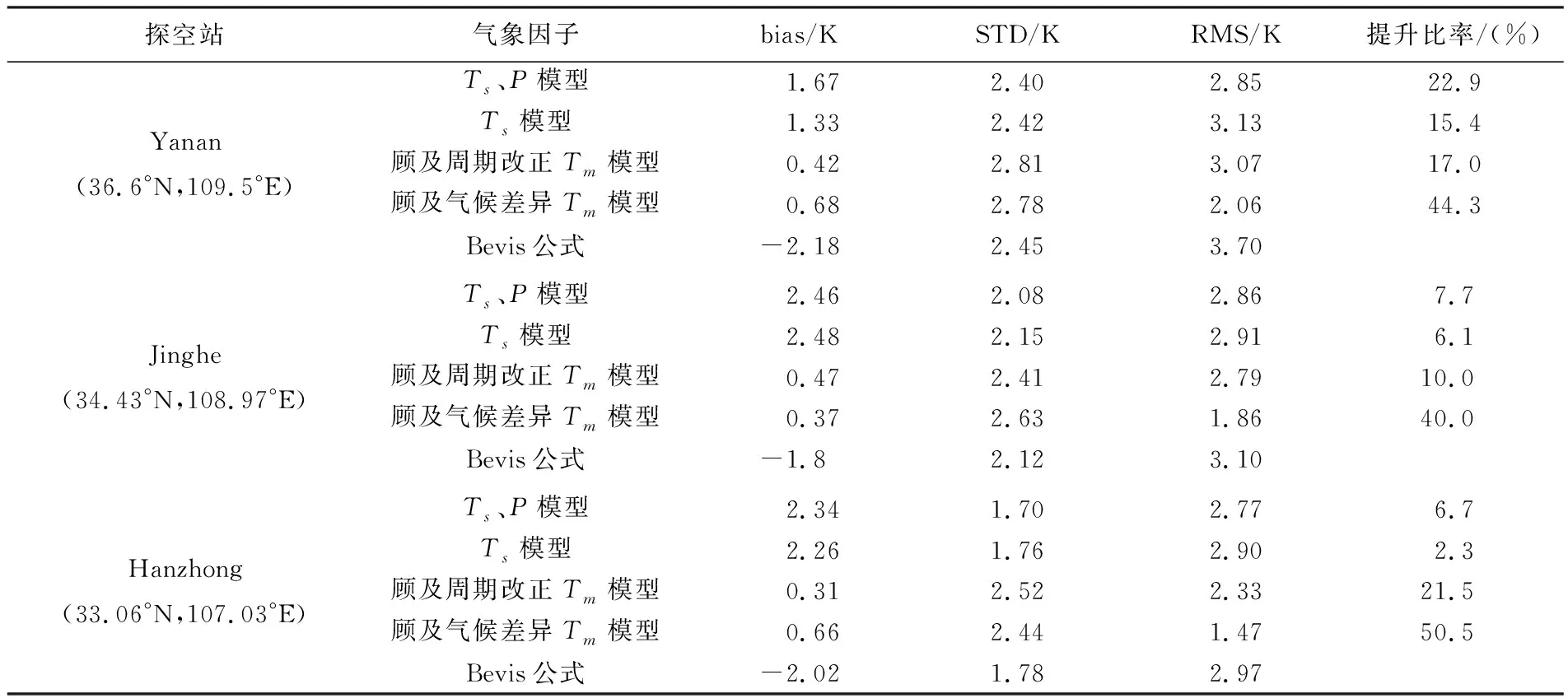
表7 模型综合精度评价

4 结 论

(1) 试验结果显示，本文利用ECMWF数据结合无线电探空数据建立的多气象因子和单气象因子的陕西省Tm模型。相较于传统仅使用无线电探空数据进行区域建模的方法，本文方法明显增加了站点空间分布，提升了数据采样率以及可靠性，使气象数据过渡更平滑，建模结果更加合理可靠。

(2) 利用研究区域内未参与建模的3个探空站的数据进行验证。陕西省区域化单因子模型比Bevis模型整体精度分别提升了2.3%、6.1%和15.4%，而加上周期性改正的Tm区域化模型，精度分别提升17%、10%和21%，提升幅度显著。这主要得益于加上周期改正Tm模型相较于传统回归模型，考虑了季节周期性改正，显著降低了模型随年积日变化和高程变化导致的误差，使得模型精度更高。

(3) 本文提出将陕西省划分为3个气候区，在不同气候区分别建立Tm回归模型，并与探空数据进行比较，外符合精度范围为1.47～2.06 K，PWV误差约为0.22～0.309 mm，相较于Bevis模型精度提升40%左右，效果明显好于对于研究区域整体建模。这说明建模时考虑不同气候差异可以有效减小模型误差，从而进一步提高模型精度。利用未参与建模的ECMWF数据对模型进行精度评估，平均RMS为3.26 K，最大RMS为3.67 K；平均STD为2.69 K，最大STD为3.19 K。模型内外符合精度较高，说明顾及气候差异的Tm模型在整个陕西省均可以获取高精度Tm。