基于非线性自回归神经网络的燃气轮机建模方法研究

李俊昆， 张绪炎， 杨志鹏

(上海发电设备成套设计研究院有限责任公司， 上海 200240)

燃气轮机控制系统需要保障燃气轮机长期安全运行，并在各类故障情况下保证机组安全停机，所以在控制系统开发过程中，需要对燃气轮机的工作情况进行各种试验，验证控制系统设计的可靠性。若直接在燃气轮机机组上进行控制系统设计验证，需要在燃气轮机本体制造完成后，才能进行控制系统验证，并且可能会因为控制系统的缺陷造成机组损伤。而采用仿真的方法对控制系统进行试验验证，不仅可以缩短控制系统研制周期，而且能降低试验风险。仿真验证是控制系统开发过程中的必要环节，可以提前发现控制系统的缺陷并进行改进；而燃气轮机控制系统仿真验证，需要建立燃气轮机数学模型。燃气轮机系统属于高度非线性的复杂系统，其建模方法通常可以分为三类：白盒建模、灰盒建模和黑盒建模。

传统的燃气轮机建模采用白盒建模的方法，以遵守质量守恒、能量守恒、动量守恒三大定律为前提，分别对压气机、燃烧室、透平和转子进行机理研究，建立机理模型，该建模方法需要厂家提供的性能曲线，一般性能曲线难以获得。文献[1]～文献[4]均是采用机理建模方法，利用部件特性曲线建立燃气轮机模型。

灰盒建模是通过简化物理特性，建立简化的燃气轮机数学模型，然后利用运行数据，通过参数辨识等方法推导出模型中的参数，该方法建立的模型通常动态特性不够精准。文献[5]～文献[7]介绍了采用传递函数建立燃气轮机模型的方法，该方法的难点是模型参数的估计，由于燃气轮机的高度非线性特点，很难用一个传递函数模型表示燃气轮机的整个运行工况。

黑盒建模则是完全根据运行数据来建立燃气轮机模型，规避了燃气轮机物理过程的描述，不需要获得压气机及透平的性能曲线，只需要获得实际运行数据就可以建立燃气轮机模型，且建模速度快、模型精度高。文献[8]介绍了采用黑盒建模进行燃气轮机建模的方法。笔者采用的非线性自回归神经网络的燃气轮机建模方法，属于黑盒建模的一种。

随着人工智能算法的发展，神经网络算法逐渐被应用到燃气轮机等热力系统的建模中。KAIADI M[9]开发了一种基于人工神经网络(ANN)的热电厂模型用于性能检测与分析，利用商业软件对网络进行交叉验证训练及测试。BETTOCCHI R等[10]研究了单转子燃气轮机的神经网络模型，并将其作为物理模型的替代，试图在准确性和鲁棒性方面探索最合适的神经网络模型。FAST M等[11]使用满负荷运行的工业单转子燃气轮机中获得的实际数据，为系统建立了具有高预测准确度的简单ANN模型，并将ANN方法与预测技术相结合，用于燃气轮机的状态监测和性能异常监测。笔者将探讨非线性自回归神经网络的基本原理，基于该方法建立燃气轮机数学模型，并对模型进行仿真验证。

1 建模的基本原理

非线性自回归神经网络是一种在静态多层感知机基础上通过引入延时单元及其反馈的循环神经网络，常用于时间序列模型。燃气轮机热力系统建模是个时序问题，因此采用该方法建立燃气轮机模型。该方法最大的特点是在输入层引入了延时单元和输出反馈，从而记录了过去的输入输出状态，再结合多层感知机的非线性映射特点，便可通过过去状态预测下一时刻状态值[8]。非线性自回归神经网络模型的定义如下：

y(t)=f(y(t-1),y(t-2), …,y(t-ny),

u(t-1),u(t-2), …,u(t-nu))

(1)

式中：y(t)为t时刻的待求变量；u(t)为t时刻外部确定的变量；f(·)是关于y(t)、u(t)的函数；ny为变量y的延时单元数量；nu为变量u的延时单元数量。下一时刻的输出参数由上一时刻的输出参数和输入参数共同回归得到。

非线性自回归神经网络由三层构成，分别是输入层、隐藏层和输出层，其基本构成见图1。输入层包含当前时刻的输入参数、前n个时刻的输入参数、前m个时刻的输出参数。而隐藏层和输出层则是由基本的感知机算法构成。

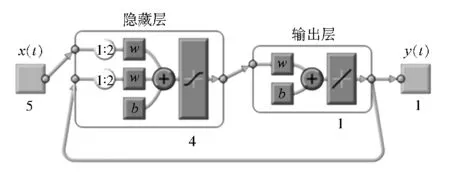
图1 非线性自回归神经网络原理

2 燃气轮机建模方法

2.1 系统分析

燃气轮机建模的主要目的是为燃气轮机控制策略的研究提供仿真对象，便于控制策略的设计验证，通过建立燃气轮机回路模型，可以分析小扰动对控制回路的影响及控制回路的稳定性。燃气轮机控制系统的主要控制回路有转速/负荷控制回路、压比限制回路、排气温度控制回路等，主要实现对转速、负荷、压比和排气温度的控制。因此，需要模型能够提供转速、负荷、压气机出口压力和排气温度等仿真信号。

笔者主要建立并网后的数学模型，并网后转速为3 000 r/min，其他参数需要由模型仿真提供。基于黑盒建模理论分析，燃气轮机建模所需的输入参数为压气机进口温度、压气机进口压力、压气机进口导叶(IGV)开度、值班阀开度和预混阀开度，输出参数为压气机出口压力、透平排气温度、输出功率。

燃气轮机控制系统仿真应用时，压气机进口温度、压气机进口压力作为外部输入参数，可以直接设定。IGV开度、值班阀开度和预混阀开度，可以用燃气轮机控制系统的指令，作为模型的输入参数。

2.2 数据采集及处理

根据建模所需要的输入参数和输出参数，获得燃气轮机电厂的运行数据。选用某430 MW级单轴联合循环机组的运行数据，其中燃气轮机型号为AE94.3A，燃料为天然气，燃气轮机的单机功率为310 MW，单机效率为40%，排烟温度为566 ℃，采用15级轴流式压气机，压比为20。

选取燃气轮机0%～38.5%(0～115.5 MW)负荷点的运行数据，该过程含有燃气轮机升负荷和降负荷的运行工况(见图2)。

图2 燃气轮机运行数据

该运行数据是从燃气轮机控制系统的历史站中获得，导出后需要进行数据处理后才能用于建模，主要处理方法如下：

(1) 以额定负荷点的数据进行归一化处理。

(2) 获得的运行数据特点为有波动的数值是毫秒级的变动，没波动的数值或波动小的数值存在时间点缺失。在进行处理时以秒为单位，对于1 s中多个采样点采用平均处理，对于缺失值，则以前一个非缺失值进行填补。

2.3 燃气轮机模型网络结构设计

燃气轮机模型的网络结构见图3。

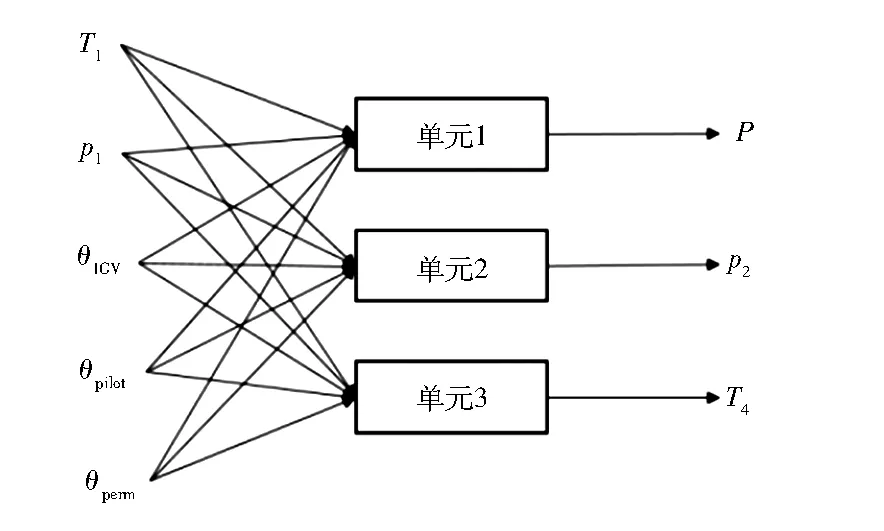
T1—压气机进口温度；p1—压气机进口压力；θIGV—进口导叶开度；θpilot—值班阀开度；θperm—预混阀开度；P—燃气轮机功率；p2—压气机出口压力；T4—透平排气温度。

上文所介绍的非线性自回归神经网络仅是单维度的网络结构，燃气轮机建模是多维度输入多维度输出的问题，以非线性自回归神经网络为基本单元，构成三维度输出的燃气轮机神经网络模型，这三个参数是燃气轮机模型的重要参数，其他参数可以利用这些参数通过简单的运算得到。

2.4 燃气轮机模型训练

神经网络训练过程通常基于迭代逼近，参数在迭代过程中依次进行更新，在每一步中，将期望的结果与实际结果进行比较，并且利用与网络结构有关的信息，对参数进行调整，以减小该组数据的预测误差。

模型训练时，网络结构先采用开环结构(见图4)，预测仿真时再采用闭环结构。

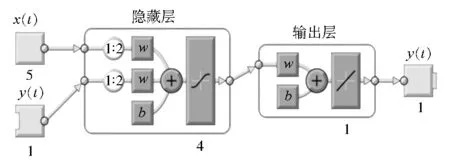
图4 非线性自回归神经网络开环结构

模型中的训练参数为权重和偏置，模型中的超参数为学习率、隐藏单元数和延迟单元数。训练参数采用随机梯度下降算法进行迭代更新。超参数以网格搜寻的方式选择确定超参数。

在使用随机梯度下降算法时，采用以下代价函数：

(2)

参数更新方法如下：

(3)

(4)

式中：C(w,b)为代价函数；y(x)为实际值；y′(x)为模型仿真值；n为样本总数；wk为第k次的样本权重；bk为第k次的样本偏置；xj为第j个样本；m为单位批量采样数；η为学习率。

在网络训练过程中，对更新的参数采用滑动平均处理，使变量的更新与一段时间内的历史值有关，以增加模型的泛化能力，增强模型的鲁棒性。

滑动平均的计算方法如下：

vt=αvt-1+(1-α)εt

(5)

(6)

式中：vt为第t次更新后的最终参数值；vt-1为第t-1次更新后的最终参数值；εt为第t次更新时计算的参数值；α为衰减率；α0为衰减率初始值；Z为模型参数更新次数。

为解决模型在训练后期振荡问题，采用指数衰减学习率，使模型在训练后期更加稳定，避免参数在最优解两侧来回振荡。

η′=η×βN/N0

(7)

式中：η′为衰减学习率；β为学习率衰减率；N为训练总步数；N0为学习率衰减步数。

在隐藏层中使用的激活函数是Tan-Sigmoid函数，输出层采用纯线性函数。Tan-Sigmoid函数是处理非线性特性的常用方法，其函数公式如下：

(8)

式中：T为缩放系数；s为位移参数。

2.5 模型测试与评估

对于训练完成的燃气轮机模型，需要用另外的燃气轮机运行数据对模型进行仿真测试，以评估模型的泛化能力。测试方式为全时间序列仿真预测，即在只给出外源输入u(t)的全时间序列值和输出参数y(t)的初始值的条件下，对y(t)的完整时间序列进行预测。

通常采用均方误差(MSE)作为评价指标，计算方法如下：

(9)

式中：yi,pred为样本i的仿真值；yi,actual为样本i实际值；nd为样本数量。

对于燃气轮机模型的建模精度，不仅要考虑均方误差，还要考虑单点最大相对误差，这样才能真实反映模型的准确度。单点最大相对误差绝对值e的定义为：

e=max(|ei|)

(10)

(11)

式中：yi,iso为样本i的额定运行工况值。

以均方误差和单点最大相对误差作为模型的评价指标，可以保证模型输出的整个时间序列中没有单点误差过大的部分。

3 动态工况建模与仿真

基于以上非线性自回归神经网络的燃气轮机建模方法，以Matlab/Simulink工具对燃气轮机进行建模仿真研究。

首先基于Matlab软件建立燃气轮机模型，并进行模型训练。训练选用12：54：00—17：27：00的运行数据，该过程燃气轮机负荷逐渐从0 MW升负荷至115.5 MW后，又下降至20 MW。训练时，选用训练数据集中的80%作为训练数据，另20%数据作为验证数据。

以压气机出口压力仿真模型训练过程示例，训练过程会随着训练次数的增加，均方误差会逐渐降低，直至趋于稳定(见图5)。

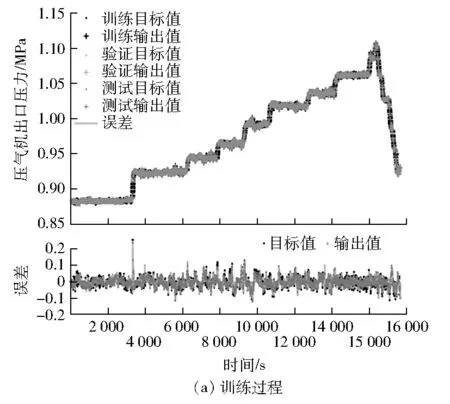
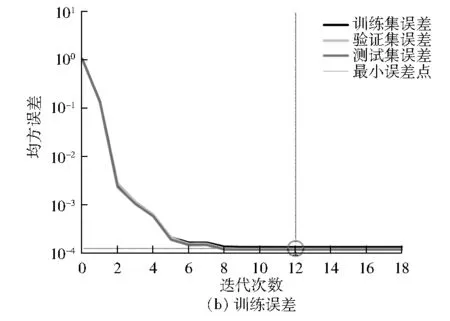
图5 压气机出口压力仿真模型训练结果

然后基于Simulink平台，以训练后的模型参数w和b搭建Simulink模型，该模型可以直接接收外界参数设定和燃气轮机控制系统的控制信号。该模型参数也可以在燃气轮机控制系统软件平台上搭建燃气轮机模型，如ABB Symphony组态工具等，在模型运算时，不需要迭代计算，模型具有较好的实时性。

搭建的Simulink燃气轮机仿真模型见图6。

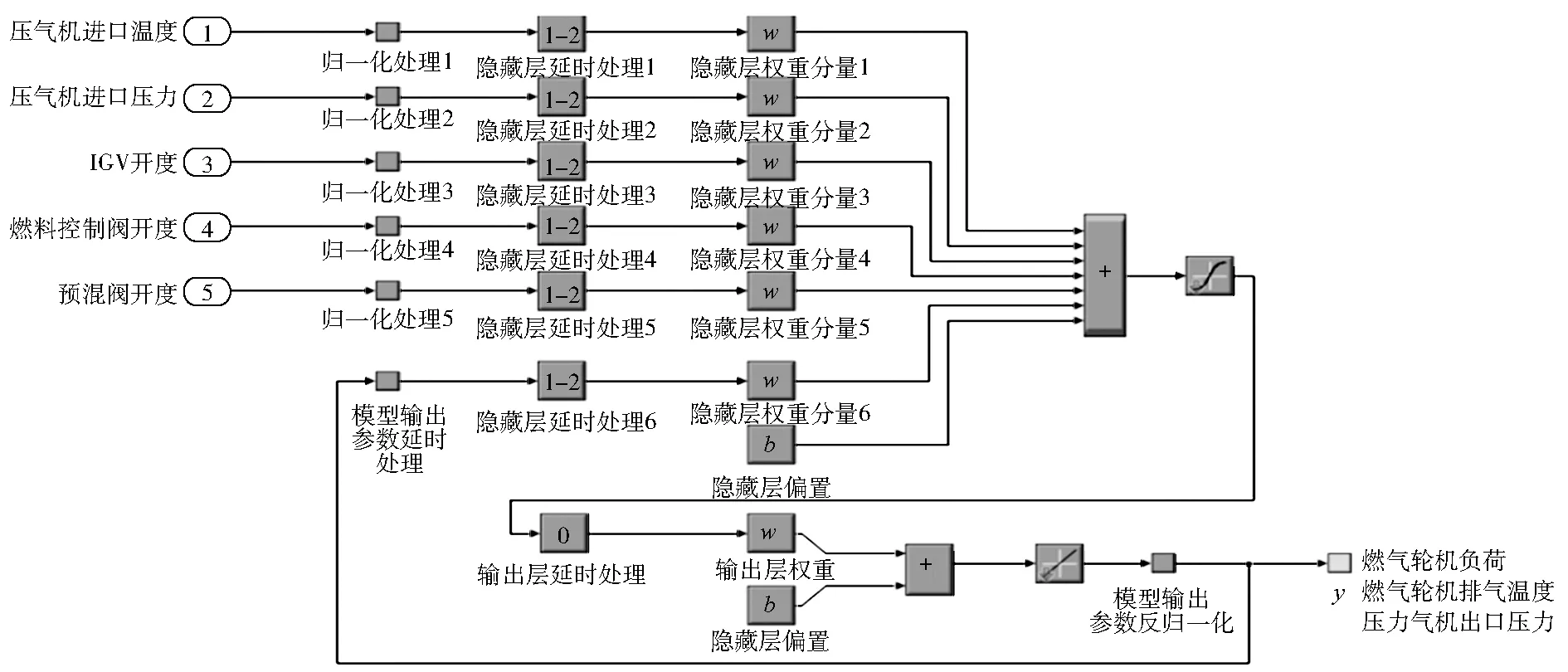
图6 燃气轮机非线性自回归神经网络模型

选取的模型超参数见表1。

表1 燃气轮机模型超参数

分别选取20～115.5 MW升负荷和115.5～20 MW降负荷的运行数据作为测试数据，以验证模型升负荷和降负荷的动态性能。

仿真结果见图7～图9。

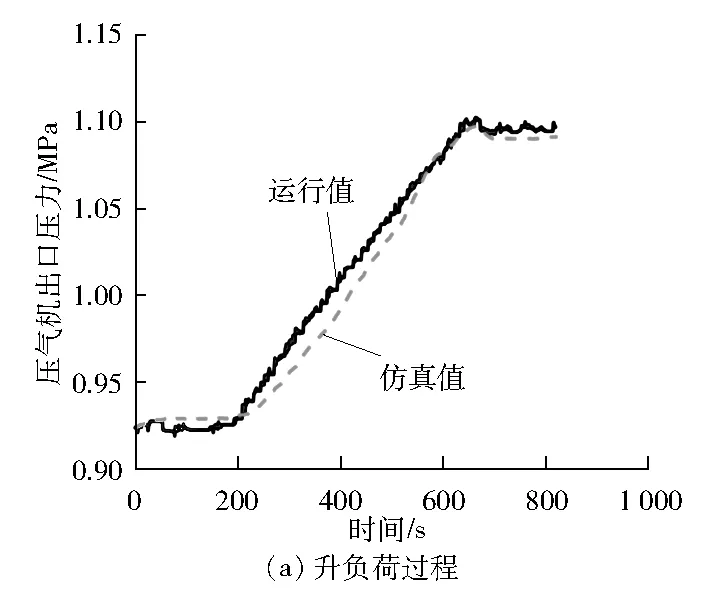
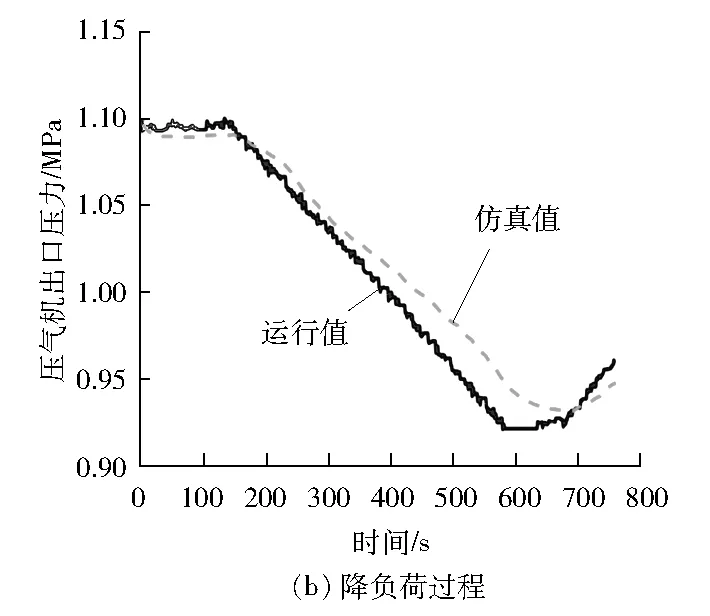
图7 压气机出口压力仿真测试结果

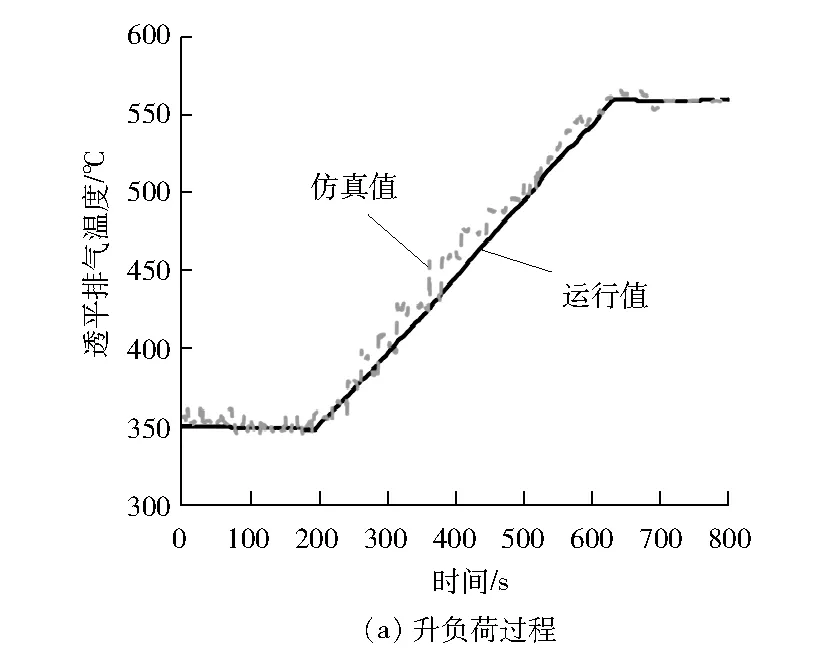
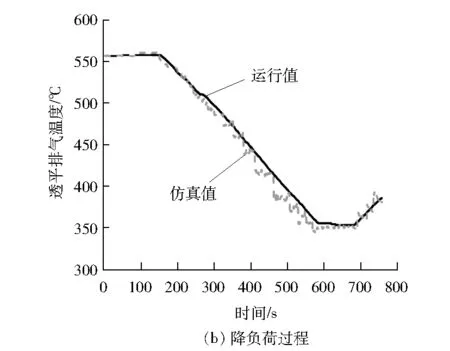
图8 透平排气温度仿真测试结果

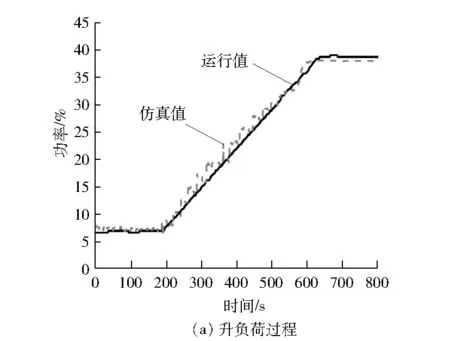
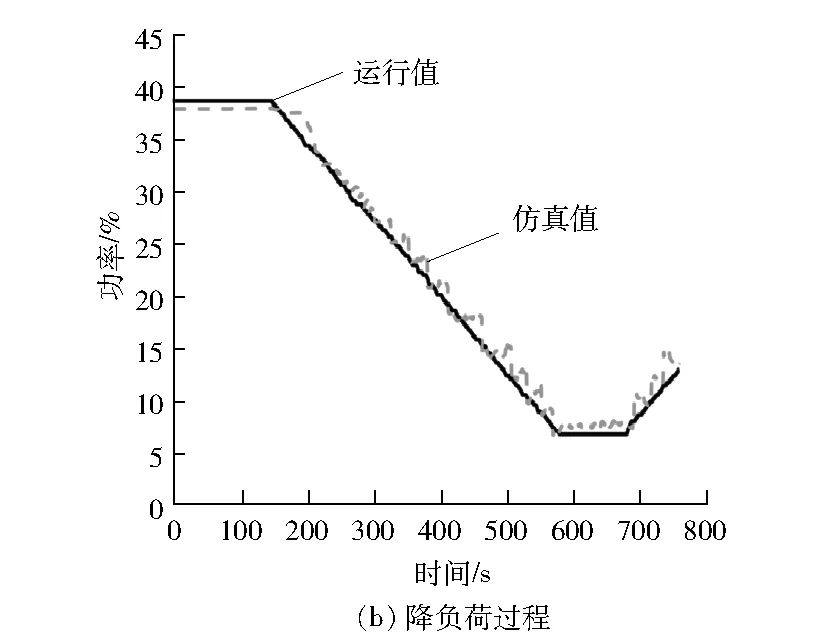
图9 功率仿真测试结果

仿真误差见表2。

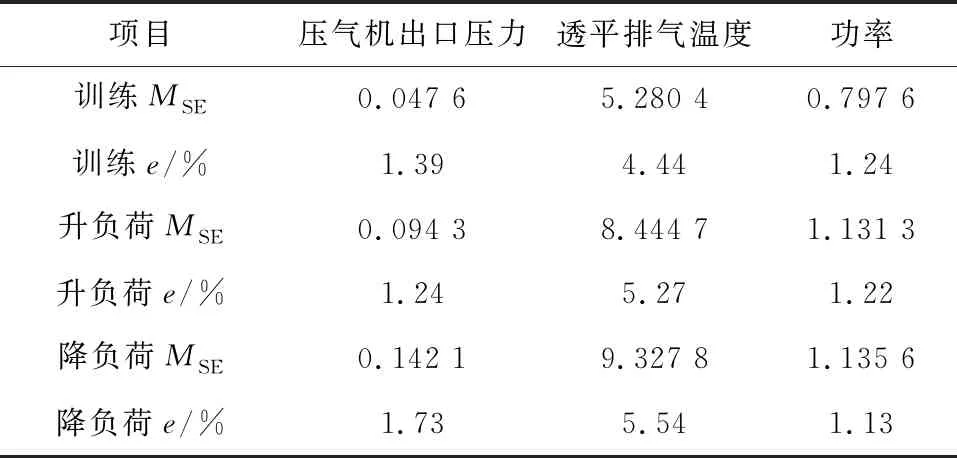
表2 燃气轮机模型仿真误差

根据仿真结果发现，无论模型中的超参数如何选取，透平排气温度和压气机出口压力的仿真的误差均无法再降低，因此需要对以上燃气轮机模型进行改进。通常情况下燃气轮机的机理建模是模块化建模，模块化建模可以很清楚地反映各模块系统的输入和输出信号(见图10)。

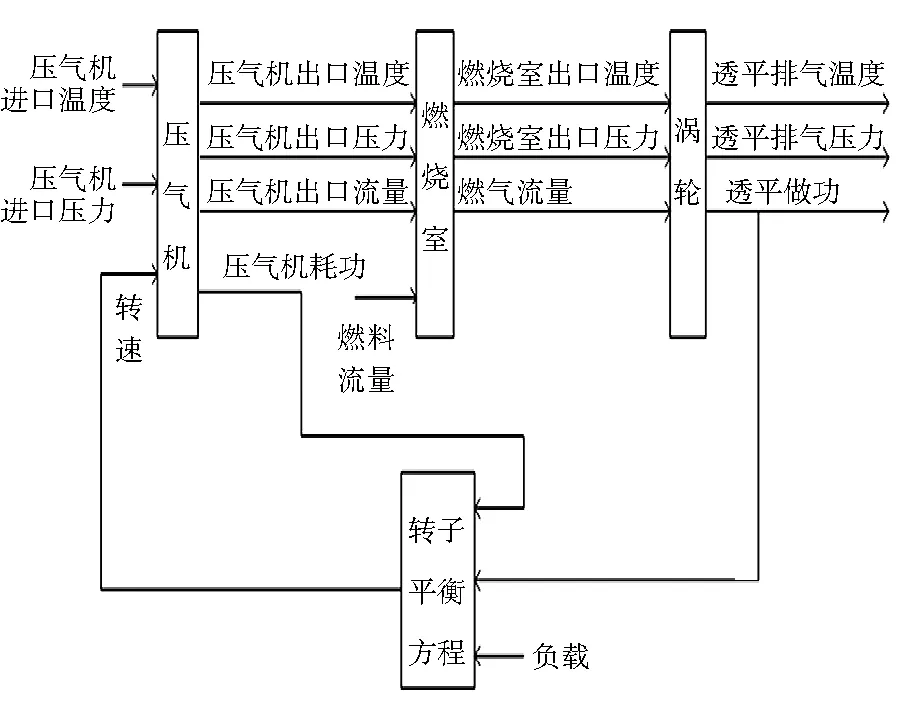
图10 燃气轮机模块化建模思想

根据模块化建模的思想，对燃气轮机非线性自回归神经网络模型的结构进行改进。在改进的模型中通过先对功率进行仿真计算，然后将功率用于其他参数仿真模型的输入中。改进后的网络结构见图11。

图11 改进的燃气轮机非线性自回归神经网络模型结构

改进的燃气轮机模型超参数见表3。

表3 改进的燃气轮机模型超参数

改进后模型的仿真结果见图12～14，仿真误差见表4。由图12～图14可以看出：改进后的燃气轮机模型对压气机出口压力和透平排气温度的仿真精度有较大提高。在建立燃气轮机非线性自回归神经网络模型时，不能简单地使用非线性自回归神经网络单元，应根据燃气轮机的特点进行模型结构的设计。

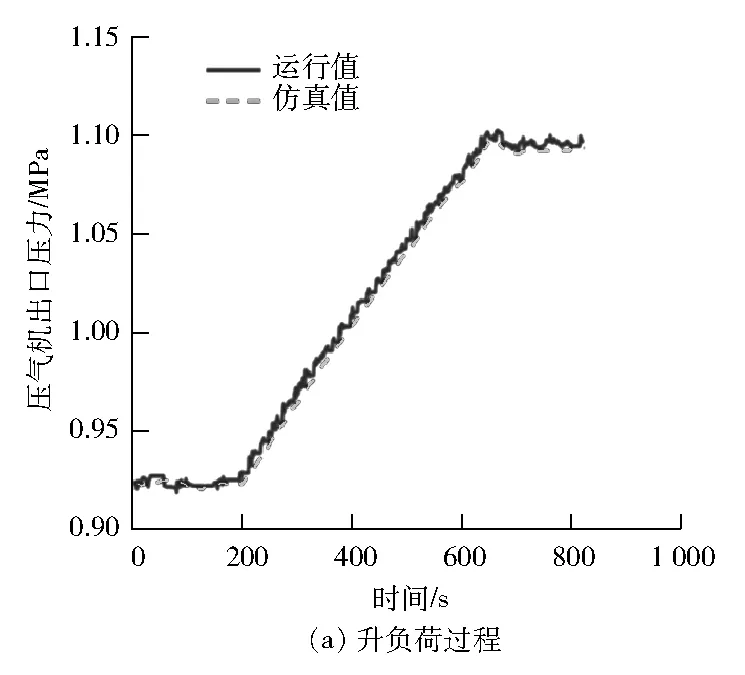
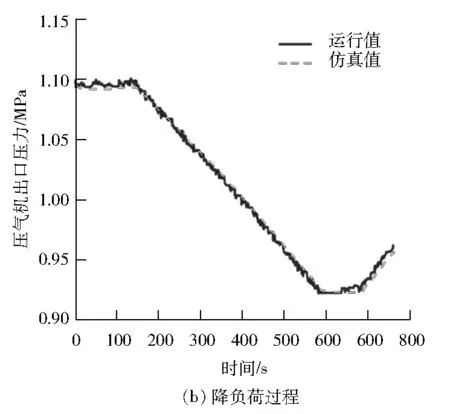
图12 压气机出口压力仿真测试结果

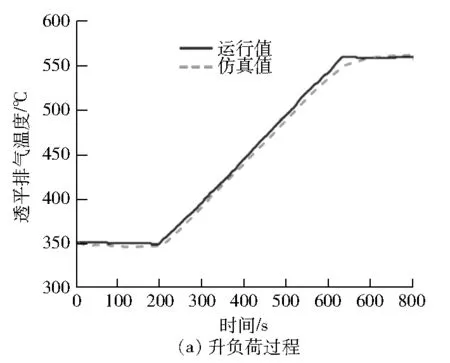
图13 透平排气温度仿真测试结果

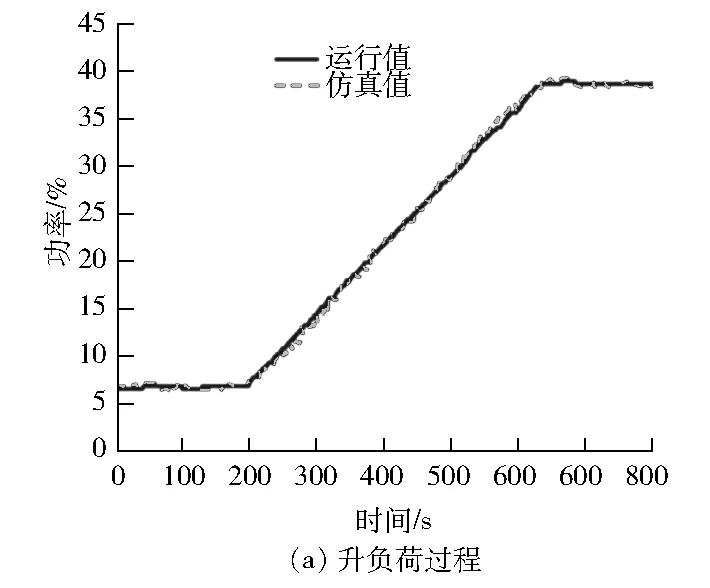
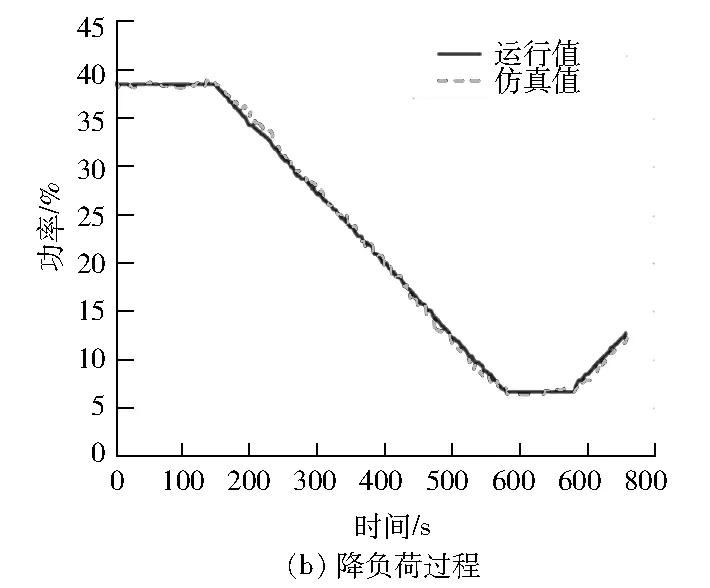
图14 功率仿真测试结果

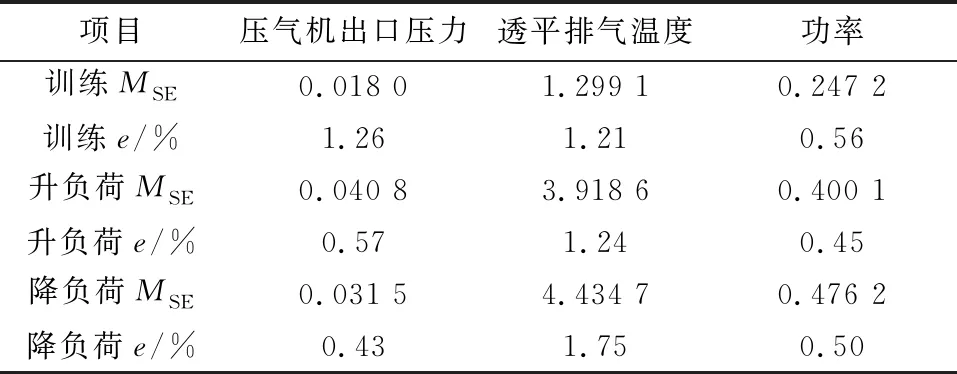
表4 改进的燃气轮机模型仿真误差

4 结语

通过对非线性自回归神经网络建模的基本原理进行阐述，给出了利用非线性自回归神经网络进行燃气轮机建模的方法，并基于某燃气-蒸汽联合循环机组的运行数据，分别对压气机出口压力、透平排气温度和功率进行了建模，最后对模型进行了仿真验证。

经验证，以实际电厂的运行数据为依据，利用该方法所建立的燃气轮机仿真模型，能够正确反映电厂燃气轮机的外特性，其仿真精度能够达到控制策略研究的要求，可以为燃气轮机控制系统的设计和控制策略的研究提供快速准确的模型，解决了常规燃气轮机机理建模方法所面临的设计参数难获取、迭代计算时间长等问题。后续仍需要获得燃气轮机全工况运行参数，以建立适用于全工况仿真的燃气轮机模型。