基于欧拉-拉格朗日模型的不同含水率生物质热解对比研究

2021-04-01于博阳尹丽洁昌庆航

发电设备 2021年2期

于博阳，尹丽洁，昌庆航

(同济大学机械与能源工程学院，上海 201800)

目前，化石能源短缺的问题逐渐严重，而生物质能作为唯一的可再生碳源[1]，其热解后的产物用途广泛[2]。随着计算机技术的进步，对于生物质在固定床内热解的研究已不仅通过实验探究方式，数值模拟也越来越受到研究者的青睐。开源软件OpenFOAM便于二次开发，所以其应用越来越广泛。关于气固两相流的模拟主要是利用双流体模型及欧拉-拉格朗日模型，双流体模型不需要计算每个颗粒的行为，可以应用在工程级别的运算上，但双流体模型难以研究颗粒输运机理，而欧拉-拉格朗日模型更适合在颗粒层面上提取具体的速度、温度等信息。

国内外的许多研究者基于拉格朗日模型对生物质热解进行了模拟。ZHOU Z Y等[3]利用计算流体动力学-离散单元法(CFD-DEM)对鼓泡流化床中的气固流动及传热进行了模拟，并与实验结果进行对比后发现，在一定条件下，单个颗粒表面的对流传热系数是恒定的，不受气相速度的影响。ZHAO Y Z等[4]采用湍动能耗散模型对带埋管的流化床气固流动及传热进行了模拟，并与实验相结合对流化床内的速度及温度分布进行了分析，结果表明CFD-DEM可较好地模拟埋管周边气固流动及传热。GENTILE G等[5]通过新的bioSMOKE求解器模拟了球体、圆柱体及长方体颗粒在热解过程中尺寸的变化，并利用bioSMOKE求解器较为准确地预测了颗粒的质量损失，证实了bioSMOKE求解器处理颗粒收缩功能的可靠性。桂莹[6]利用OpenFOAM软件模拟了煤粉射流燃烧的过程，结果表明煤粉颗粒尺寸会影响燃烧强度和燃烧稳定性。LI T等[7]基于OpenFOAM软件模拟了高温下生物质的热解，并引入了新的颗粒收缩模型来更精确地模拟热解过程中颗粒粒径的变化，与等体积模型和简化的等密度收缩模型相比，新的模型对颗粒热解过程中粒径变化的模拟结果与实验数据更接近。

上述研究主要围绕在固相较为稀疏的工况下不同物质热解与燃烧的过程，而当固相较为稠密时，以上模型由于缺少对固相体积分数的考虑，故将其应用于固相较为稠密的固定床反应器不太适合。因此，笔者引入固相体积分数，并基于新开发的求解器对固定床反应器内不同含水率(水分质量分数)生物质的热解过程进行模拟，旨在探究水分的存在对热解过程中颗粒温度、温度分布均匀性及有效传热系数的影响。

1 模型的建立及求解

1.1 控制方程

在OpenFOAM软件中，基于欧拉-拉格朗日模型的求解器有许多，其中：DPMFoam求解器适用于固相稠密工况，但缺少了传热及化学反应的模型；coalchemistryFoam求解器适用于热解及燃烧的工况，但由于忽略了固相体积分数的影响，故不适合稠密的固相固定床的模拟。故在以上两个求解器的基础上，对coalchemistryFoam求解器进行二次开发，引入固相体积分数，得到的新求解器将更适合稠密固相的工况。改进后的求解器对于气相采用欧拉法处理，颗粒相则采用拉格朗日法处理，具体的气固流体动力学方程见表1[8]和表2[8-10]，反应产物包括气体(CO2、CO、CH4、H2和H2O)[11]、可凝挥发分(生物质油和焦油)和木炭[12]。

表1 气相控制方程

表2 颗粒相控制方程

1.2 边界条件

图1为计算模型示意图，模拟对象为一个常压固定床热解炉(见图1(a))，热解时物料堆积在反应器底部，模拟时仅建立物料堆积段的模型(见图1(b))，模拟区域高度为0.1 m，直径为0.08 m。物料为生物质颗粒，粒径为2 mm，初始内部充满氮气，反应器壁面提供热量，颗粒初始温度均为300 K，其中前0.1 s为颗粒的喷入过程，此时固定床内温度及壁面温度均为300 K，0.1 s后壁面开始加热，加热温度为873 K，研究含水率分别为0%、5%、10%和15%时的热解过程。利用ICEM软件划分网格后，将网格文件导入OpenFOAM软件进行计算，网格总数约为18 000(保证颗粒尺寸小于网格)，自动调整计算时间步长，生物质颗粒从计算域的顶部喷入反应器内。

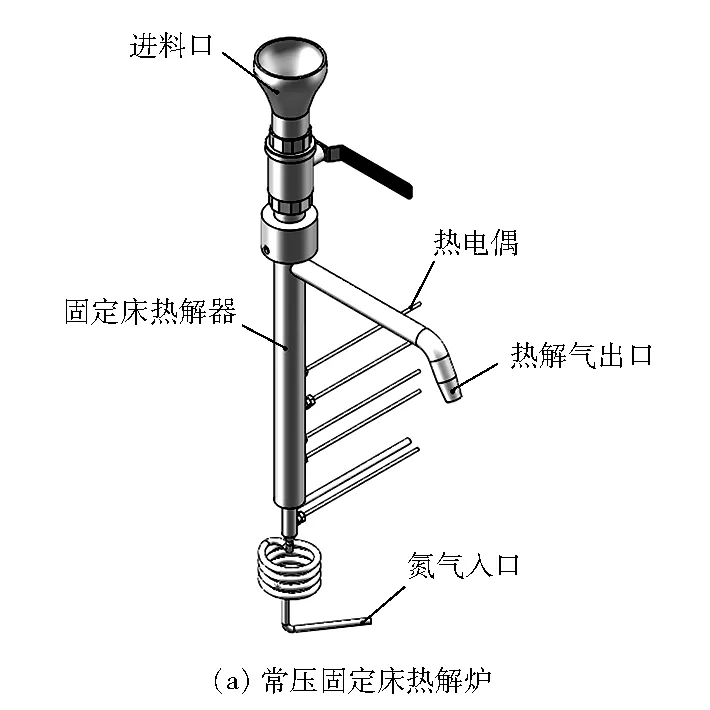
图1 计算模型示意图

1.3 求解过程

在欧拉-拉格朗日模型中，利用守恒方程求解连续相，通过计算大量遵循牛顿第二定律的粒子求解颗粒相。使用的求解器中动量守恒方程与压力校正耦合采用了PIMPLE算法，首先更新密度，并计算不包含压力相的速度，其次由式(1)导出压力方程，求解压力方程并校正非正交性，更新表面通量，最后计算连续性方程，根据新计算的压力更新速度，而动能和因压力产生的能量相也将更新用于能量的计算。颗粒相的位置更新由式(5)确定，颗粒温度则由式(3)、(6)计算得到。

2 结果与分析

2.1 模型验证

图2为不同条件下反应器内固相剩余质量分数随颗粒平均温度变化的模拟结果和实验结果，其中：图2(a)所设置的热解温度为873 K，含水率为0%，升温速率为20 K/min；图2(b)为生物质大颗粒热解实验结果[13]与模拟结果的对比，采用大颗粒热重实验台对厘米级别的生物质颗粒进行了热重实验，先将大颗粒热重实验台以20 K/min的升温速率加热至993 K，然后迅速将盛有颗粒的容器放入实验台，模拟设置与文献一致。

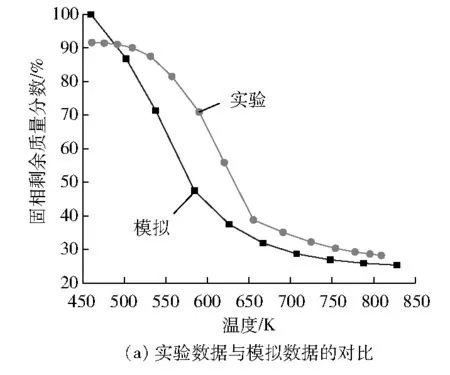
图2 模拟结果与实验结果的对比

由图2可得：热解过程可分为3个阶段，即刚开始少量颗粒达到热解温度，颗粒质量缓慢减少，随后大部分颗粒开始热解，颗粒质量迅速下降，最后少部分颗粒未完成热解，挥发分少量析出的阶段，并且模拟结果与实验结果能够较好地吻合。与实验结果曲线相比，模拟结果曲线存在左移的现象，主要是模拟时设置的热解温度是单个颗粒温度并不是颗粒平均温度，而不同颗粒的温度在同一时刻存在差异，所以当部分颗粒达到热解温度开始热解时，容器内颗粒平均温度低于所设置的热解温度。

2.2 颗粒温度的分布

图3为颗粒粒径为2 mm、含水率为0%、热解温度为873 K时，颗粒热解开始(固相质量分数为99%)及热解完成(固相质量分数为35%)时反应器底部的温度分布。由图3可得：颗粒整体温度分布呈现从壁面向中心逐渐降低的趋势，部分区域出现靠近中心处颗粒温度高于外围的现象，可能是当0.1 s时壁面维持873 K开始加热，颗粒从反应器顶部喷入，此时还有少部分颗粒仍在下落过程中，受到辐射传热的影响，这部分颗粒升温较快(部分已达到热解温度)，当这些颗粒落入底部后会与周围温度较低的颗粒进行传热，故在部分区域出现了温度较高的颗粒。

图3 颗粒温度的分布

2.3 含水率的影响

图4为不同含水率的生物质热解时颗粒平均温度随时间的变化，颗粒总数为25 000，颗粒粒径均为2 mm。由图4可得：与不含水的生物质相比，含水的生物质颗粒升温明显变慢，且含水率越高，热解所需的时间越长。当颗粒平均温度在400～500 K时，颗粒的升温明显有放缓的趋势，且含水率越高，升温的时间越长，主要是因为水分的存在抑制了颗粒的升温过程。同样将颗粒升温至700 K，与含水率为0%的颗粒相比，含水率为5%、10%、15%的颗粒所需的时间分别多了26.1%、52.1%、73.9%。

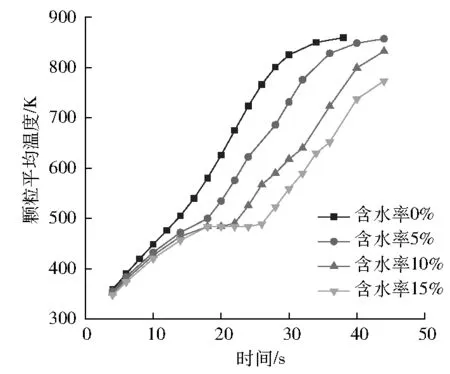
图4 颗粒平均温度随时间的变化

表3为不同含水率的颗粒在不同热解阶段颗粒数量随温度变化的分布。

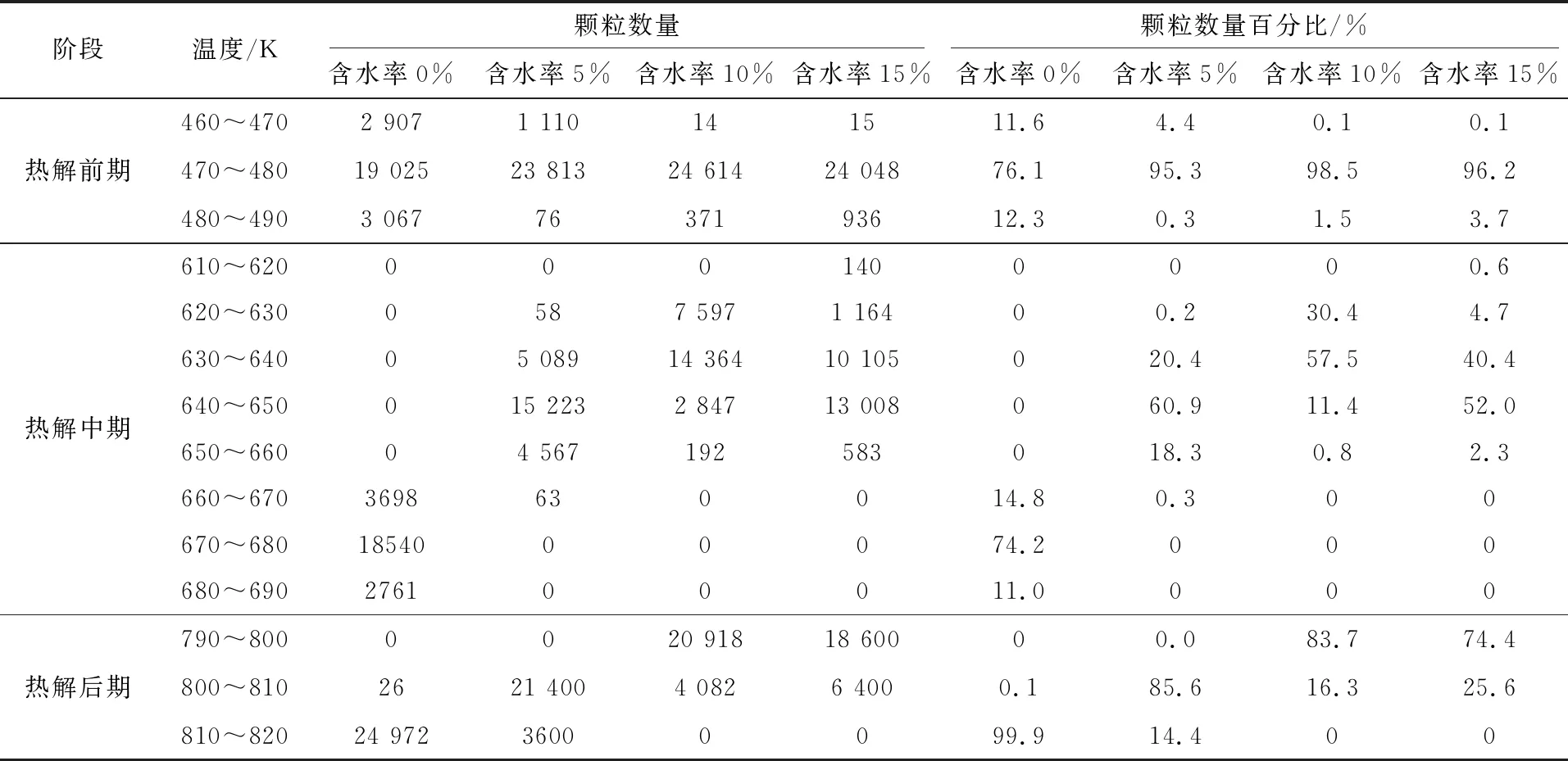
表3 不同热解阶段颗粒数量随温度变化的分布

由表3可得：在热解前期，水分的存在使得颗粒更集中于470～480 K。在剧烈热解阶段即热解中期，含水率越高，颗粒温度分布越不均匀，具体表现为：当含水率为0%时，颗粒主要集中于670～680 K，其数量百分比为74.2%；当含水率为15%时，颗粒主要集中于640～650 K，其数量百分比为52.0%。随着含水率的升高，在热解中期的颗粒温度分布也越发不均匀。最后，在热解即将结束的阶段即热解后期，颗粒温度分布无明显变化规律。水分的存在对热解前期及后期的颗粒温度分布的均匀性没有明显影响。

图5为热解过程中颗粒平均温度标准差随颗粒平均温度的变化。由图5可得：在剧烈热解阶段，颗粒平均温度在500～650 K时，颗粒温度分布处于最不均匀的阶段，且含水率越高，温度分布越不均匀。含水率为15%、10%、5%、0%时，最大平均温度标准差分别为14.4 K、9.3 K、7.6 K、6.4 K，主要是因为汽化后的水蒸气储存了大量汽化潜热，这部分热量会传递给颗粒，使部分颗粒升温较快。同时在热解后期，平均温度标准差逐渐减少，且含水率对热解后期颗粒温度分布的均匀性无明显影响，可能是因为此时水分已经全部蒸发。

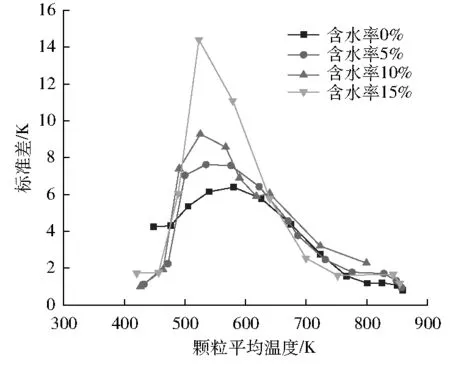
图5 颗粒平均温度标准差随平均温度的变化

在热解过程中颗粒吸收的热量用于颗粒温度的升高和提供热解反应所需的热量，图6为不同热解温度对有效传热系数的影响，有效传热系数是指从颗粒进入反应器加热开始至热解结束的平均传热系数。

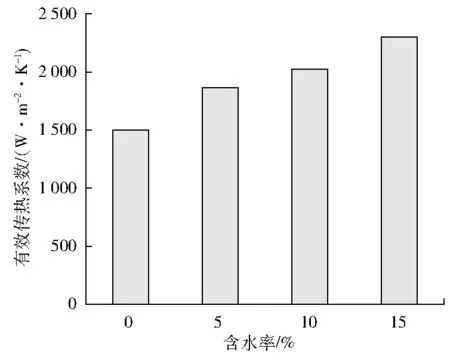
图6 有效传热系数随含水率的变化

由图6可得：含水率越高，有效传热系数越大。含水率为0%时，有效传热系数为1 498 W/(m2·K)；含水率为15%时，有效传热系数为2 202 W/(m2·K)。将含水率为5%时的有效传热系数作为比较基准，可得：含水率为10%时，有效传热系数增加了8.3%；含水率为15%时，有效传热系数增加了18.1%。这是因为水蒸气储存了大量的汽化潜热，可强化气流与颗粒间的传热过程。