不同剪切变形下橡胶隔震支座竖向压缩刚度试验研究

金建敏，肖 骥，刘彦辉，冯德民，谭 平，黄襄云

(1.广州大学 工程抗震研究中心，广州 510405；2.藤田技术研究中心，厚木 243-0125)

历次大地震中，隔震结构均表现出良好的隔震效果，使得隔震技术得到快速的发展和应用。在众多隔震装置中，由于橡胶隔震支座性能相对稳定、构造简单、造价相对较低，已成为隔震结构中最常用的隔震装置，其中以天然橡胶支座及铅芯橡胶支座为代表性的橡胶隔震支座应用最为广泛。目前，进行隔震结构地震响应分析时，橡胶隔震支座竖向压缩刚度通常采用线弹性压缩刚度，采用水平零位移时在0.7倍～1.3倍设计压应力下的测试结果，在整个地震作用过程中，竖向压缩刚度保持不变。但是在真实地震作用下，橡胶隔震支座发生水平剪切变形，有效承载面积发生变化，且由于整体倾覆弯矩的影响，橡胶隔震支座实际压应力变化范围远大于±30%的设计压应力。因此，有必要研究不同剪切变形下橡胶隔震支座竖向压缩刚度，以及研究压应力变化范围对竖向刚度的影响。

在国外，Ryan等[1]采用第一形状系数(S1)为15.0、第二形状系数(S2)为2.86的直径180 mm铅芯橡胶支座，以及S1为20.0、S2为4.0的直径176 mm的高阻尼橡胶支座，研究了不同水平剪切变形下铅芯橡胶支座和高阻尼橡胶支座的竖向压缩刚度。Warn等[2]采用S1为10.17、S2为2.53的直径152 mm天然橡胶支座，以及S1和S2分别为12.67和2.53的直径152 mm的铅芯橡胶支座，进行了竖向压缩刚度受水平剪切位移影响的试验研究。Ryan和Warn等的研究结果表明，基于双弹簧模型的竖向压缩刚度计算公式可较好反映橡胶隔震支座的竖向压缩刚度随水平剪切变形的增大而减小趋势，但与建筑结构中常用的橡胶隔震支座相比较，试验所采用的橡胶隔震支座的S1及S2有一定的差异。在国内，刘文光[3]采用橡胶剪切模量为0.55 MPa、S1分别为23.3和24.0、S2分别为4.8和5.0的直径300 mm天然橡胶支座，以及S1分别为27.8和30.0、S2分别为4.8和5.0的直径300 mm铅芯橡胶支座，进行了压应力为10 MPa下的竖向压缩刚度受水平剪切变形影响的试验研究。王建强等[4-5]采用橡胶剪切模量为0.392 MPa、S1和S2分别为20.0和5.0的直径200 mm铅芯橡胶支座，以及橡胶剪切模量为0.8 MPa、S1和S2分别为8.66和6.67的直径200 mm高阻尼橡胶支座，进行了压应力及水平剪应变对竖向压缩刚度影响的试验研究。王维等[6]针对S1为35、S2为5.1的G3橡胶隔震支座进行了不同压应力下的竖向压缩刚度测试试验(剪应变为0)，试验结果显示，随着压应力的增加，竖向压缩刚度增大。本文在以上研究的基础上，研究橡胶隔震支座在不同水平剪切变形状态下的竖向压缩刚度理论计算方法，基于双弹簧模型，提出了改进的求解不同剪切变形状态下橡胶隔震支座竖向压缩刚度理论计算公式。然后，采用建筑结构中常用的S1>30、S2=5系列(G4)天然橡胶支座及铅芯橡胶支座，进行了不同压应力及不同剪切变形下的压缩性能试验，研究不同水平剪切变形状态下的橡胶隔震支座竖向压缩刚度。

1 竖向压缩刚度理论计算方法

纯压缩状态下，水平剪切位移为零，橡胶隔震支座的竖向压缩刚度KV可用式(1)求得

(1a)

(1b)

(1c)

式中：Ecb为橡胶的修正压缩弹性模量;Ec为橡胶的压缩弹性模量;E0为橡胶的弹性模量；κ为修正系数;Eb为橡胶的体积弹性模量，可取为1 960 MPa;A为支座面积;Tr为内部橡胶总厚度。

文献[7]以橡胶隔震支座有效承载面积(支座顶部与底部重叠部分的面积)Ae代替橡胶隔震支座面积A，当水平剪切位移为X时，橡胶隔震支座竖向压缩刚度计算公式为

(2)

(3)

式中，D为支座直径。

式(3)可简化为

(4a)

(4b)

虽然基于橡胶隔震支座有效承载面积计算其竖向压缩刚度的公式简单易行，但该公式缺乏严格的理论基础。为了获得理论严密的橡胶隔震支座不同水平剪切变形下竖向压缩刚度，Koh等[8]提出了一种模拟橡胶支座力学性能简化的双弹簧模型，该模型可用于计算不同水平剪切位移时的支座竖向压缩刚度，由剪切弹簧、转动弹簧、无摩擦滚轴、T形刚性单元及刚性底板(底部铰接)组成，如图1所示。

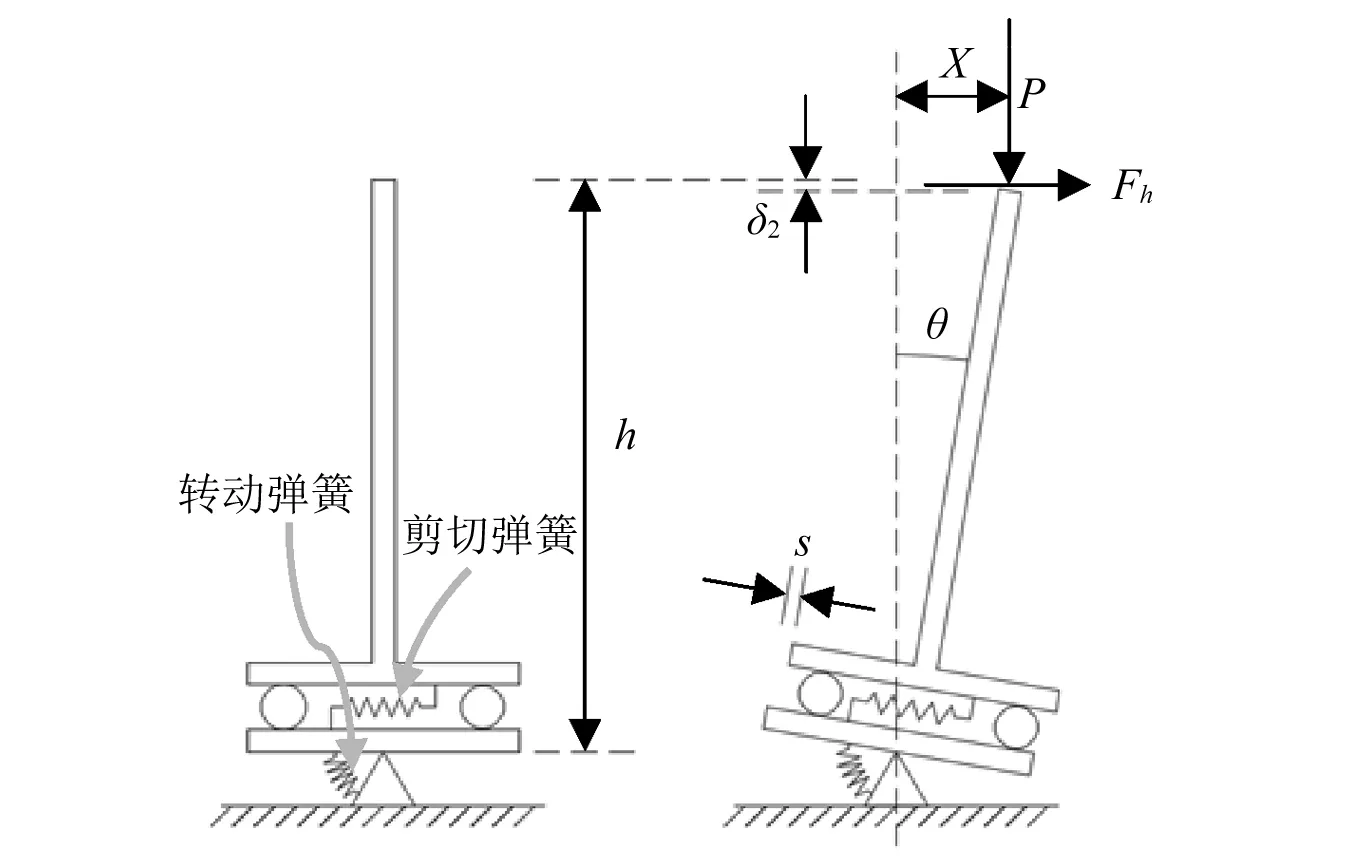
图1 双弹簧模型Fig.1 Two-spring model

在小转角时，双弹簧模型的平衡方程为

-Pθ+Khs=Fh

(5a)

(Kθ-Ph)θ-Ps=Fhh

(5b)

式中：Fh为水平力；P为竖向压力；h为内部橡胶及内部钢板的总厚度；Kh为剪切弹簧的刚度；s为剪切弹簧的变形；Kθ为转动弹簧的刚度；θ为转动弹簧的转角。

Kh可表示为

(6)

Kθ可表示为

(7a)

(7b)

(7c)

Is=Ih/Tr

(7d)

PE=π2ErbIs/h2

(7e)

式中：Erb为橡胶的修正弯曲弹性模量;Er为橡胶的弯曲弹性模量;I为支座截面惯性矩;PE为欧拉屈曲荷载。

支座水平剪切位移X及竖向位移δ由式(8)求出

X=s+hθ

(8)

(9)

式中:δ1为竖向压力所产生的竖向位移;δ2为支座水平位移所产生的竖向位移。

设PS=GAs=Khh，由式(5a)、式(5b)、式(8)和式(9)，联立可求得

(10)

(11)

由于PE远大于P及PS，式(11)可简化为

(12)

将式(12)代入式(9)，由KVX=dP/dδ，可得

(13)

Kelly[9]将Ecb取为Erb的3倍，即Ecb=3Erb，对于有中孔的橡胶隔震支座，内、外半径分别为R0及R，A=π(R2-R02)，I=π(R4-R04)/4，设a=R0/R，代入式(13)可求得KVX为

(14)

式中，r为回转半径。式(14)在OpenSees中得到应用，分别为Isolator2spring截面[10]、ElastomericX单元及LeadRubberX单元[11-12]所采用。

由Ecb和Erb的计算公式可见，二者均受到第一形状系数的影响。为了研究第一形状系数对Ecb与Erb比值的影响，由式(1b)和式(7b)可得

(15)

对于建筑隔震常用的G4橡胶隔震支座，橡胶剪切模量G=0.392 MPa，κ取为0.85，Eb取为1 960 MPa，橡胶的弹性模量E0，天然橡胶支座取为1.18 MPa(即按E0=3G取值)，铅芯橡胶支座取为1.44 MPa(考虑铅芯的影响)。将以上参数代入式(15)，可得到Ecb/Erb与橡胶隔震支座第一形状系数S1关系曲线如图2所示。由图2可见，当橡胶隔震支座S1仅在5～10时接近3，在S1约大于6后，随着S1的增加，Ecb/Erb越来越小于3，当S1达到30以上后，天然橡胶支座取Ecb/Erb为3与实际的Ecb/Erb相差47.2%以上，铅芯橡胶支座取Ecb/Erb为3与实际的Ecb/Erb相差54.7%以上。目前我国相关规范规定建筑橡胶隔震支座S1一般需大于15[13]，在实际工程实践中，为了进一步提高橡胶隔震支座竖向承载力及竖向稳定性，S1的取值大多在30左右或以上，显然采用式(14)计算建筑橡胶隔震支座不同剪切变形下的竖向压缩刚度是不合适的，将带来较大的计算误差。

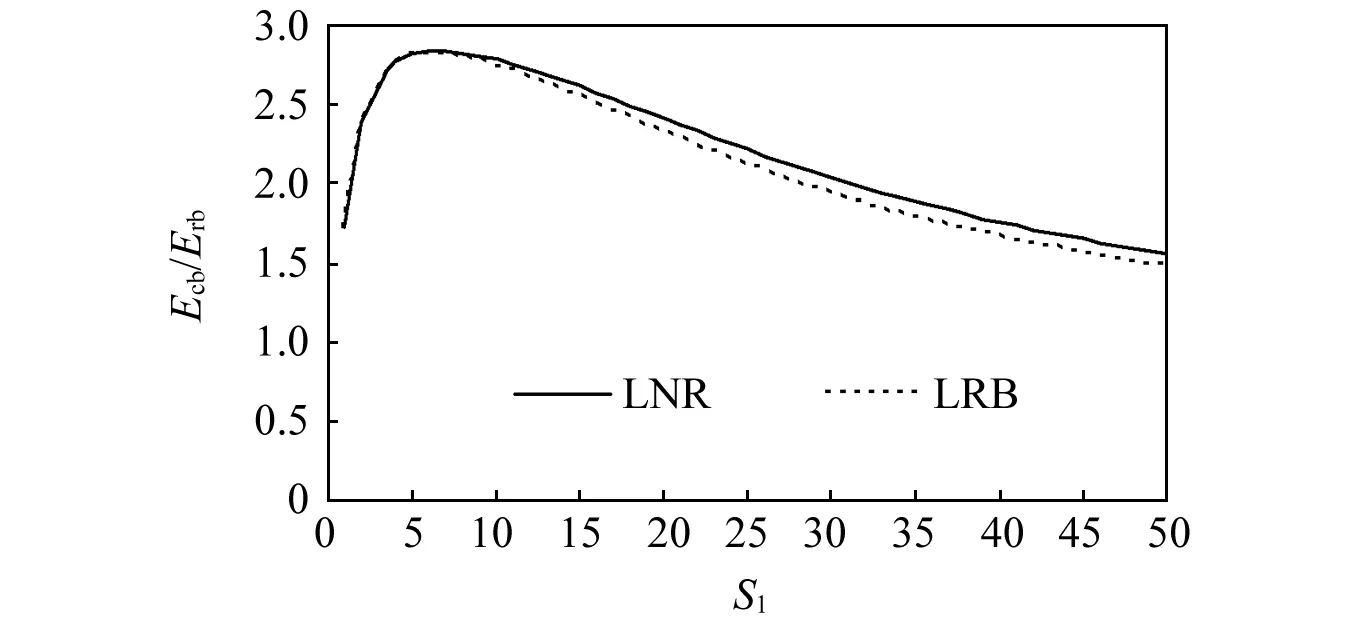
图2 Ecb/Erb-S1曲线Fig.2 Ecb/Erb-S1 curves

为了提高Kelly提出的橡胶隔震支座不同剪切变形下的竖向压缩刚度计算精度，将式(15)代入式(13)，可获得改进的橡胶隔震支座不同剪切变形下的竖向压缩刚度计算公式

(16)

橡胶隔震支座中孔对KVX/KV计算结果的影响随中孔半径与支座半径的比值a增大而增大；当a为0.2，即使X=2R(支座顶部与底部重叠部分的面积为零，实际应用中允许的支座水平剪切位移小于支座半径2倍)，采用式(14)时，忽略橡胶隔震支座中孔影响计算KVX/KV，误差仅为3.3%，此误差为橡胶隔震支座水平剪切变形过程中的最大误差；而由于式(16)Ecb与Erb比值小于3，采用式(16)时，忽略橡胶隔震支座中孔影响计算KVX/KV，误差相比式(14)将有所减小。因此，采用推导的式(16)计算橡胶隔震支座不同剪切变形下的竖向压缩刚度可不考虑中孔的影响。

2 竖向压缩刚度试验

2.1 试验橡胶隔震支座

制作了直径为300 mm的2个天然橡胶支座(LNR300-1,LNR300-2)及2个铅芯橡胶支座(LRB300-1,LRB300-2)，橡胶剪切模量为0.392 MPa(G4)，LNR300-1及LRB300-1由同一厂家制作生产，LNR300-2及LRB300-2由另一厂家制作生产，单层内部橡胶厚度均为2 mm，由于2个厂家的模具高度及生产工艺的不同，单层内部钢板厚度(LNR300-1及LRB300-1的单层内部钢板厚度为2 mm)及天然橡胶支座的中孔有所不同(LNR300-1的中孔为30 mm)，支座参数见表1。

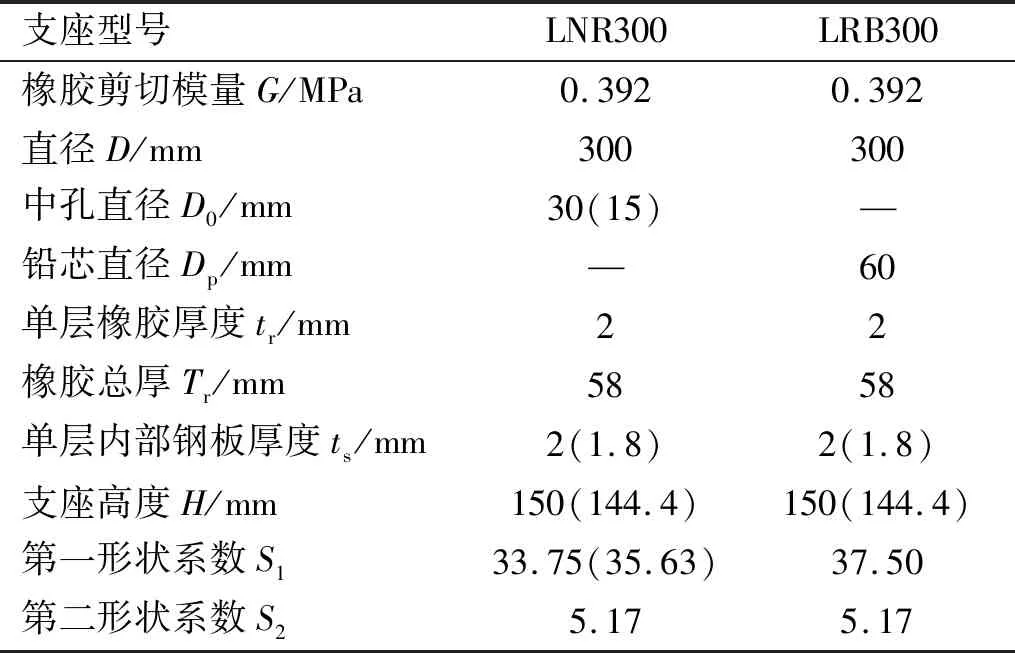
表1 支座参数Tab.1 Parameters of isolators

2.2 加载设备及试验工况

试验加载设备为广州大学工程抗震中心的拉压剪试验机，设备竖向最大压荷载500 t、拉荷载300 t，水平最大荷载100 t。根据GB/T 20688.1—2007《隔震橡胶支座试验方法》[14]中规定的竖向压缩刚度的剪应变相关性试验方法，加载剪应变依次为0γ0,0.5γ0,1.0γ0和1.5γ0，其中γ0为设计剪应变，本文取为100%，0为基准剪应变。考虑到在强震中，橡胶隔震支座剪应变往往超过200%，所以4个支座均完成了剪应变0%～200%的竖向压缩刚度的剪应变相关性试验，并选择LNR300-1进行剪应变250%，LRB300-1进行剪应变250%及300%的竖向压缩试验。

由于橡胶隔震支座设计压应力σ0可取为10 MPa，12 MPa及15 MPa[15]，所以LNR300-1，LNR300-2及LRB300-2，分别进行了加载压应力为10 MPa±30%，12 MPa±30%及15 MPa±30%的竖向压缩刚度的剪应变相关性试验；为兼顾竖向压缩刚度的压应力相关性试验(即压应力变化范围对竖向压缩刚度的影响)，参考《隔震橡胶支座试验方法》，设计压应力σ0取为12 MPa，基准加载条件σ0±30%，在LRB300-1支座进行不同剪应变试验时，加载压应力为12 MPa±30%，12 MPa±50%，12 MPa±100%的竖向压缩刚度压应力相关性试验。

试验时，首先用水平作动器将橡胶隔震支座推到指定剪应变对应的水平剪切位移，然后进行相应不同压应力下的竖向压缩刚度测试，在橡胶隔震支座四周布置4个竖向位移传感器，支座竖向变形取4个竖向位移传感器实测值的平均值，各工况试验结果均以第3圈试验结果为准，各支座的试验工况见表2。

表2 试验工况Tab.2 Test conditions

3 试验结果分析

首先进行纯压缩状态下(剪应变γ=0%)竖向压缩刚度测试试验，测试试验结果见表3，由表3可见，在不同设计压应力下，橡胶隔震支座竖向压缩刚度随设计压应力的增大而增大；LRB300-1支座在设计压应力12 MPa下，随着橡胶隔震支座压应力变动范围的增大，竖向压缩刚度逐步减小。

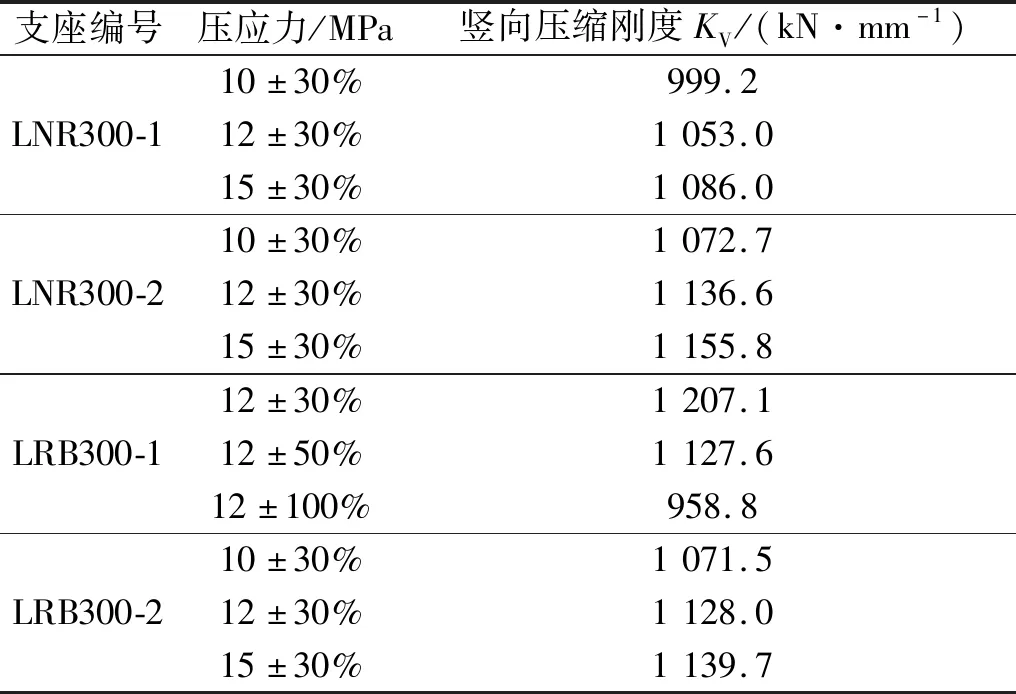
表3 试验结果Tab.3 Test results

然后进行橡胶隔震支座不同剪切变形状态下竖向压缩刚度的测试，如图3所示，图4为不同剪应变时，实测的LNR300-1及LRB300-1支座竖向压力-竖向位移曲线(12 MPa±30%，第3圈)，图中竖向位移未考虑由水平剪切位移的影响，即竖向压力为零时，竖向位移为零，由图4可见，随剪应变的增大，橡胶隔震支座竖向压缩刚度呈现下降的趋势。

图3 不同剪切变形的隔震支座试验Fig.3 Test of isolators under different shear deformation

图4 竖向压力-竖向位移曲线(12 MPa±30%)Fig.4 Vertical compressive force-vertical displacement curves(12 MPa±30%)

图5为不同加载压应力下和不同剪应变工况下支座竖向压缩刚度测试结果。图6给出了加载压应力条件相同的情况下，以剪应变γ=0%的试验结果为基准值，归一化后不同剪应变的竖向压缩刚度(偏压竖向刚度与纯压竖向刚度比值，KVX/KV)试验结果，以及采用不同计算公式计算的结果。由图5及图6可见，LNR300-1，LNR300-2及LRB300-2支座，不同设计压应力(10 MPa，12 MPa，15 MPa) 下，无论是天然橡胶支座或是铅芯橡胶支座，不同剪应变工况的竖向压缩刚度试验结果均表明随剪应变的增大，即随水平剪切位移的增大，竖向压缩刚度实测值逐渐变小，支座竖向压缩刚度随设计压应力的增大而增大；LRB300-1支座的竖向压缩刚度试验结果(12 MPa±30%，12 MPa±50%，12 MPa±100%)显示，当压应力变化范围不同时，竖向压缩刚度仍随水平剪切位移的增大而逐渐变小。加载压应力12 MPa±30%的不同剪应变下竖向压缩刚度试验，与纯压缩状态下试验结果相比较，剪应变γ=200%时，2个天然橡胶支座的竖向压缩刚度分别降低了21.2%和30.2%，2个铅芯橡胶支座的竖向压缩刚度分别降低了14.9%和21.1%；随着剪应变进一步增大，剪应变γ=250%时，LNR300-1及LRB300-1支座的竖向压缩刚度降低程度增大，分别由21.2%增大为27.4%，14.9%增大为21.9%；剪应变γ=300%时，LRB300-1支座的竖向压缩刚度降低程度进一步增大为27.7%。LRB300-1的测试结果表明，在设计压应力12 MPa下，随压应力变动范围的增大，竖向压缩刚度实测值逐渐变小；剪应变相同时，与压应力12 MPa±30%的试验结果相比较，压应力12 MPa±50%的试验结果略有降低，降低程度为3.4%～6.6%，压应力12 MPa±100%的试验结果进一步降低，降低程度为18.4%～22.3%；以压应力12 MPa±30%下(剪应变γ=0%)测试结果为基准值，在剪应变γ=300%时，12 MPa±100%的试验结果为678.2 kN/mm，降低程度达到43.8%。

图5 竖向压缩刚度试验结果Fig.5 Test results of vertical compressive stiffness

同时由图6可见，基于有效承载面积Ae计算橡胶隔震支座竖向压缩刚度的方法(式(2))与不同压应力和不同剪应变工况的试验结果相比较，高估了竖向压缩刚度随剪应变增大而减小的趋势，计算误差较大且随着剪应变的增大而变大，与LNR300-1及LRB300-1支座试验结果(12 MPa±30%，剪应变γ=250%)相比较，基于支座有效承载面积计算隔震支座竖向压缩刚度的误差分别为43.6%及47.6%；与基于有效承载面积计算隔震支座竖向压缩刚度的方法相比较，既有的基于双弹簧模型计算橡胶隔震支座竖向压缩刚度的方法(式(14))与试验结果更为相符，但该计算方法在剪应变150%以上时，其计算误差变得较大，与LNR300-1及LRB300-1支座试验结果(12 MPa±30%，剪应变γ=250%)相比较，计算误差分别为35.2%及40.1%；本文提的改进的基于双弹簧模型计算橡胶隔震支座竖向压缩刚度的方法(式(16))计算精度明显高于基于有效承载面积Ae计算橡胶隔震支座竖向压缩刚度的方法和既有的基于双弹簧模型计算橡胶隔震支座竖向压缩刚度的方法，与LNR300-1及LRB300-1支座试验结果(12 MPa±30%，剪应变γ=250%)相比较，提出的改进的基于双弹簧模型计算橡胶隔震支座竖向压缩刚度的方法计算误差分别为19.9%及22.6%，对于LNR300-1及LRB300-1支座，在压应力12 MPa±30%和剪应变250%时，该竖向压缩刚度计算方法减小既有的基于双弹簧模型计算橡胶隔震支座竖向压缩刚度的方法的计算误差分别为15.3%和17.5%，计算精度提高至1.77倍。

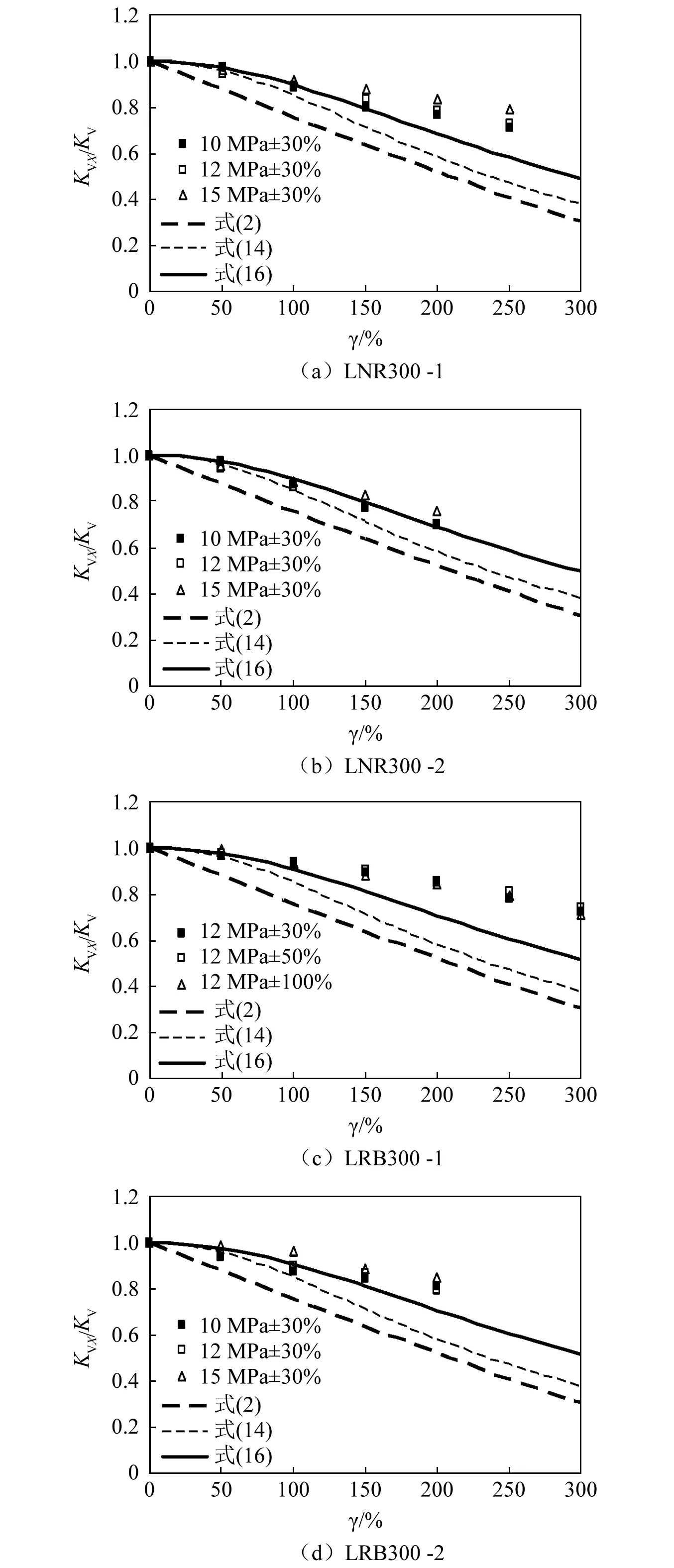
图6 试验结果与计算结果对比Fig.6 Comparison between test results and calculation results

4 结 论

本文基于双弹簧模型，提出了改进的计算不同剪切变形状态下橡胶隔震支座竖向压缩刚度计算公式，然后采用建筑结构中常用的天然橡胶支座及铅芯橡胶支座，进行了不同压应力及不同剪切变形下的压剪力学性能试验，通过理论与试验研究，得到以下结论：

(1)天然橡胶支座和铅芯橡胶支座的竖向压缩刚度随剪应变增大而逐渐减小；隔震支座竖向压缩刚度随设计压应力的增大而增大；设计压应力相同的条件下，随压应力变动范围的增大，竖向压缩刚度变小。

(2)基于有效承载面积的竖向压缩刚度计算公式虽能反映竖向压缩刚度随剪应变增大而逐渐减小的趋势，但与试验结果相比误差较大。既有的基于双弹簧模型的竖向压缩刚度计算公式计算精度优于基于有效承载面积的竖向压缩刚度计算公式，但在150%以上剪应变时，也存在误差较大的问题，可见，对于建筑结构中常用的天然橡胶支座及铅芯橡胶支座，橡胶的修正压缩弹性模量Ecb不应取为修正弯曲弹性模量Erb的3倍。

(3)提出的改进的基于双弹簧模型的橡胶隔震支座竖向压缩刚度计算公式能较好地计算不同剪切变形下支座的竖向压缩刚度，计算精度优于基于有效承载面积的竖向压缩刚度计算公式以及既有的基于双弹簧模型的竖向压缩刚度计算公式，在剪应变250%时，有效地提高既有的基于双弹簧模型的竖向压缩刚度计算公式的计算精度。