基于OHF Elman-AdaBoost算法的滚动轴承故障多时期诊断方法

卓鹏程，夏唐斌,2，郑美妹，郑 宇，奚立峰,2

(1.上海交通大学 机械与动力工程学院，上海 200240；2.上海交通大学 机械系统与振动国家重点实验室，上海 200240)

随着我国工业水平的不断发展,工业领域的设备在不断趋向大型化、复杂化。大型复杂装备的平稳安全运行关系到生产安全的关键核心[1]。滚动轴承作为大型复杂设备的重要组成部分，其性能退化或失效将影响整机性能甚至导致设备非计划停机，造成严重经济损失甚至重大人员伤亡。据统计，约45%～55%的旋转机械故障是由于滚动轴承的损伤所造成的[2]。然而当滚动轴承处于故障初期时，其故障信息往往表现比较模糊，振动信号异常不明显。同时因为缺乏对轴承故障程度的掌控，往往当滚动轴承处于故障晚期时才有明显表征，诊断滞后会造成严重的失效风险。因此，对于滚动轴承故障中早期的诊断则十分必要，可以有效地预先设计维修与更换方案。在当前制造业中，对滚动轴承建立退化模型或进行剩余寿命预测需要大量全生命周期状态数据，且预测模型与实际退化状态之间的误差较大。因此，实现滚动轴承实时精确的故障初期、中期及晚期诊断，可以有效降低事故发生率，对于提高企业的制造运维和健康管理水平具有重要意义。

滚动轴承故障诊断技术目前主要包括两个方面：故障信号提取与故障模式识别。在故障信号提取方面，目前常用的方法有Hilbert-Huang变换、小波变换(wavelet transform,WT)、经验模态分解(empirical mode decomposition,EMD)与集合经验模态分解(ensemble empirical mode decomposition,EEMD)等[3-6]。EEMD对于滚动轴承振动信号有着较好的去噪效果，可以有效地提取出滚动轴承早期故障信息。在故障模式识别方面，常用的方法包括概率统计方法、支持向量机(support vector machine,SVM)和人工神经网络(artificial neural networks,ANN)等[7-12]。滚动轴承故障早期数据具有非线性、强干扰与数据源复杂等特性，概率统计方法与支持向量机均存在一定的局限性，目前神经网络由于其自适用能力与容错性，成为最热门的滚动轴承故障诊断方法。Shi等[13]基于Elman神经网络提出OHF Elman (output hidden feedback Elman) 网络，并证明了OHF Elman相较Elman神经网络的优越性。但是，单个OHF Elman神经网络无法保证对所有测试样本都有较好的适用性。为了实现更为精确的滚动轴承全样本故障诊断方法，Singh等[14]通过Bagging (bootstrap aggregating) 算法将朴素贝叶斯(Naïve Bayes)与决策树结合，提高了对多类分类的准确度。Li等[15]提出了一种AdaBoost-BP检测器，实现了对液压执行器内部泄露故障的自动评估。鉴于滚动轴承不同故障时期特征信号的相似性，本文提出一种基于OHF Elman神经网络与AdaBoost的新型集成算法，以适用早期故障信号的多样性与鲁棒性。

为了对滚动轴承不同时期的故障进行有效的诊断，本文提出整合EEMD与OHF Elman-AdaBoost算法的整体诊断框架，重点将集成算法引入故障诊断领域。鉴于Bagging算法是通过选择不同的样本数据训练得到不同的弱学习器，弱学习器的个数与样本数量有关，而AdaBoost算法则是调整样本权重得到不同的弱学习器。相比较而言，AdaBoost算法原理更易理解且更具有适用性，因此，本文选择以OHF Elman神经网络作为弱回归器，利用AdaBoost集成算法构造一个强回归器，从而实现对滚动轴承故障诊断误差的显著降低。

1 问题描述

以滚动轴承振动信号作为原始数据进行故障多时期诊断。在故障诊断中，不仅需要诊断出滚动轴承所处故障时期，同时也需要准确剖析出故障源。本研究全面分析了滚动体、内圈与外圈这三种主要故障部件，因此所涵盖的滚动轴承故障多时期诊断可转化为多分类问题，如图1所示。

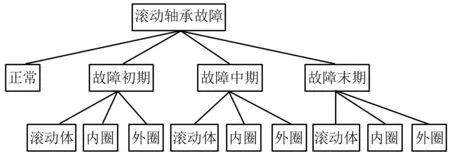
图1 滚动轴承故障分类图Fig.1 Classification diagram of rolling bearing faults

由于滚动轴承振动信号的非平稳性、非线性，且掺杂不同程度的噪声，选用EEMD进行模态分解与信号重构，从振动信号中提取有效的特征向量。在此基础上，选择OHF Elman神经网络作为故障模式识别的方法，并结合AdaBoost算法集成得到强回归器，研究对滚动轴承进行更为准确地故障诊断。所构建的技术方法框架如图2所示。

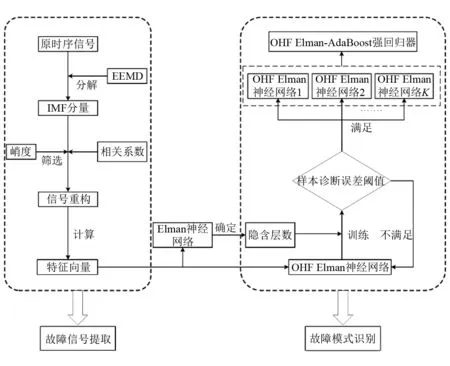
图2 滚动轴承故障诊断技术框架图Fig.2 Technical framework of fault diagnosis for rolling bearing

该框架主要由故障信号提取与故障模式识别两部分组成。故障信号提取方面，采用峭度与相关系数作为EEMD模态分解得到基本模态分量(intrinsic mode function,IMF)筛选的判断准则。故障模式识别方面，通过Elman神经网络的诊断误差效果确定OHF Elman的隐含层数，从而保证两种神经网络的参数一致性，进而证明OHF Elman神经网络相较于Elman神经网络的优越性。在与AdaBoost算法集成时，采用样本误差阈值作为样本权重变化的判断准则。利用所构建的机制，最终形成的OHF Elman-AdaBoost强回归器在全样本数据上可实现更为准确的故障诊断水平。

OHF Elman基于Elman神经网络增加输出层对隐含层的反馈实现处理动态数据的能力。鉴于单个OHF Elman神经网络无法保证对所有测试样本都有较好的适用性，本研究为了提供更为精确地诊断滚动轴承全样本故障，将AdaBoost集成算法引入故障诊断领域。所建立的OHF Elman-AdaBoost算法的优势在于：

(1) 选择以OHF Elman神经网络作为诊断算法核心，以其独特的反馈结构，拥有对数据的动态处理能力，特别适用于滚动轴承的故障诊断。

(2) AdaBoost算法通过集成多个弱学习器得到一个强学习器，从而拥有对样本数据更强的学习能力。

(3) 以OHF Elman神经网络作为弱回归器，结合AdaBoost算法集成出新的强回归器，从而实现对滚动轴承全样本数据更有效的故障诊断。

2 诊断方法建模

2.1 OHF Elman神经网络模型

人工神经网络在理论上可以任意精度逼近任意非线性映射，无需建立精确的数学模型，一旦输入输出数据确定，神经网络即可挖掘输入输出之间的连接关系。与BP神经网络相比，Elman神经网络在结构上增加了一层隐含层对输入层的反馈，具有更高的动态性与准确性。而OHF Elman神经网络则是在Elman神经网络基础上增加了输出与隐含层的反馈，进一步提高了网络对历史数据的记忆功能。OHF Elman结构如图3所示。

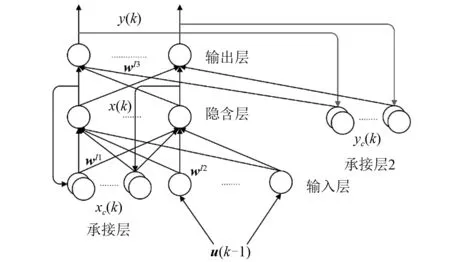
图3 OHF Elman网络结构示意图Fig.3 Illustration of OHF Elman network structure

OHF Elman神经网络的数学模型

x(k)=f(wI1xc(k)+wI2u(k-1))

(1)

xc(k)=αxc(k-1)+x(k-1)

(2)

yc(k)=γyc(k-1)+y(k-1)

(3)

y(k)=g(wI3x(k)+wI4yc(k))

(4)

式中：g(·)为线性函数；α，γ均为反馈增益因子，其取值范围为(0,1)；f(t)通常取为sigmoid函数,即

(5)

误差函数为

(6)

式中：k为系统迭代步数；u为r维输入向量；x，xc分别为n维隐含层与承接层输出；y，yc分别为m维输出层与承接层2的输出；wI1，wI2，wI3，wI4分别为n×n，n×r，m×n，m×m维权值矩阵；yd为实际输出。

2.2 原AdaBoost算法模型

AdaBoost是一种常用于提高数据训练性能的机器学习集成算法。一般AdaBoost算法在使用的时候会选择一种弱学习器，目前常用的有分类树、支持向量机与神经网络等。AdaBoost主要是通过在下一次弱学习器训练之前适当调整训练数据分布中的权重，来强调先前学习效果错误或者学习误差较大的样本。因此，通过集成每一步的弱学习器可以更好地对测试数据进行预测诊断[16-17]。

AdaBoost算法主要解决分类与回归问题，分类算法目前主要有AdaBoost基本算法、AdaBoost M1与AdaBoost M2算法，分别适用于两类分类、多类离散分类与多类连续分类问题。回归算法主要有AdaBoost R2与AdaBoost RT算法。AdaBoost算法构建强学习器时比较灵活且结果不易发生过拟合。AdaBoost R2模型的流程如下。

弱回归器个数：K

弱回归器：Gj(X),j=1,…,K

输出：强回归器G(X)

(1) 训练集样本权重初始化：w1(i)=1/N,i=1,…,N

(2)j=1,…,K循环训练

① 对样本进行训练并得到弱回归器Gj(X)，计算弱回归器Gj(X)在样本数据上的最大误差Ej

Ej=maxi|Oji-Yji|,i=1,…,N

(7)

式中，Oji为弱回归器Gj(X)对训练集Xi的预测结果。

(8)

(9)

(10)

上面分别为线性误差、平方误差与指数误差情况下的相对误差计算公式。

③ 计算弱回归器Gj(X)的误差率ej

(11)

④ 计算弱回归器Gj(X)的权重系数αj

(12)

⑤ 训练集样本权重更新

(13)

(14)

(3) 强回归器G(X)获得

(15)

2.3 OHF Elman-AdaBoost算法模型

为了进一步提高对滚动轴承故障多时期诊断的准确性，本研究构建了一种OHF Elman-AdaBoost算法：选择以OHF Elman神经网络作为弱回归器，反复训练OHF Elman神经网络预测输出，通过AdaBoost算法集成得到一个由多个OHF Elman神经网络组成的强回归器。

OHF Elman-AdaBoost模型流程如下。

弱回归器个数：K

弱回归器：OHF Elman神经网络Cj(X)，j=1,…,K

输出：强回归器H(X)

(1) 训练集样本权重初始化：w1(i)=1/N，i=1,…,N

(2)j=1,…,K循环训练

① 初始化ej=0，对样本Xi与wj(i)(i=1,…,N)进行弱回归器Cj(X)训练，并计算弱回归器Cj(X)在各个样本数据上的绝对误差εi

(16)

② 计算弱回归器Cj(X)的误差率ej

ej=∑wj(i)，εi>τ

(17)

式中，τ为预先设定的阈值，高于τ即为预测不准确。

③ 计算弱回归器Cj(X)的权重系数αj

(18)

④ 训练集样本权重更新

(19)

(20)

(3) 弱回归器Cj(X)权重系数归一化

(21)

(4) 强回归器H(X)获得

(22)

OHF Elman-AdaBoost模型与AdaBoost R2模型的区别：①在计算弱回归器的误差率部分，OHF Elman-AdaBoost模型使用样本的绝对预测误差阈值进行样本划分，因为当阈值设置合理时，小于阈值的样本预测误差已经可以达到要求，只考虑预测误差较大样本会加快模型迭代；②在计算弱回归器的权重系数部分，OHF Elman-AdaBoost模型借鉴了AdaBoost分类模型，通过对数函数减慢弱分类器权重系数的变化，从而得到更好的强回归器；③在训练样本权重更新部分，OHF Elman-AdaBoost模型选择使用不同的常数系数来更新，这样会加快样本权重的变化，也是对第二点的呼应，中和弱分类器权重变化速度，从而加快强回归器的集成。

3 案例分析

3.1 数据集说明

本研究采用自凯斯西储大学轴承中心的滚动轴承振动数据，即采用SKF轴承进行的0.017 78 cm,0.035 56 cm和0.053 34 cm故障直径的实验。分析电机转速为1 797 r/min，采样频率为12 kHz的内圈、滚动体与外圈故障数据(包括正常模式)，共有十种故障模式。每种故障状态选择120 000个样本点，正常状态选择240 000个样本点。该实验是采用电火花加工将单点故障引入试验轴承，0.017 78 cm,0.035 56 cm和0.053 34 cm均为故障点的直径，现实设备的滚动轴承一旦发生单点故障，故障点的直径会随着故障时间的发展而增大。因此，本文选择故障直径为0.017 78 cm的故障状态为故障初期，故障直径为0.035 56 cm的故障状态为故障中期，故障直径为0.053 34 cm的故障状态为故障晚期。下文中b017，b035，b053代表直径为0.017 78 cm,0.035 56 cm和0.053 34 cm下的滚动体故障；IR017，IR035，IR053代表直径为0.017 78 cm,0.035 56 cm和0.053 34 cm下的内圈故障；OR017，OR035，OR053代表直径为0.017 78 cm,0.035 56 cm和0.053 34 cm下的外圈故障。

3.2 数据处理

轴承故障振动信号通常表现为周期性瞬态脉冲，为了有效地显示时频域内的特征，采样信号应至少覆盖两个或三个周期。考虑采样频率和特征频率，本文选择2 000个样本点代表故障振动信号的特征。因此，按时序每2 000个样本点设定为一组输入数据，即每种故障状态(涵盖滚动体、内圈、外圈的各自初期、中期、晚期故障共九种)各有60组样本数据，正常状态有120组样本数据。

以2 000个样本点正常信号的EEMD分解波形图为例，其结果如图4所示。从上至下，10个波形图分别为2 000样本点分解出的9个IMF分量和一个残余分量R。从图4中可见，各个IMF分量之间基本消除了模态混叠且残余分量R单调递减。

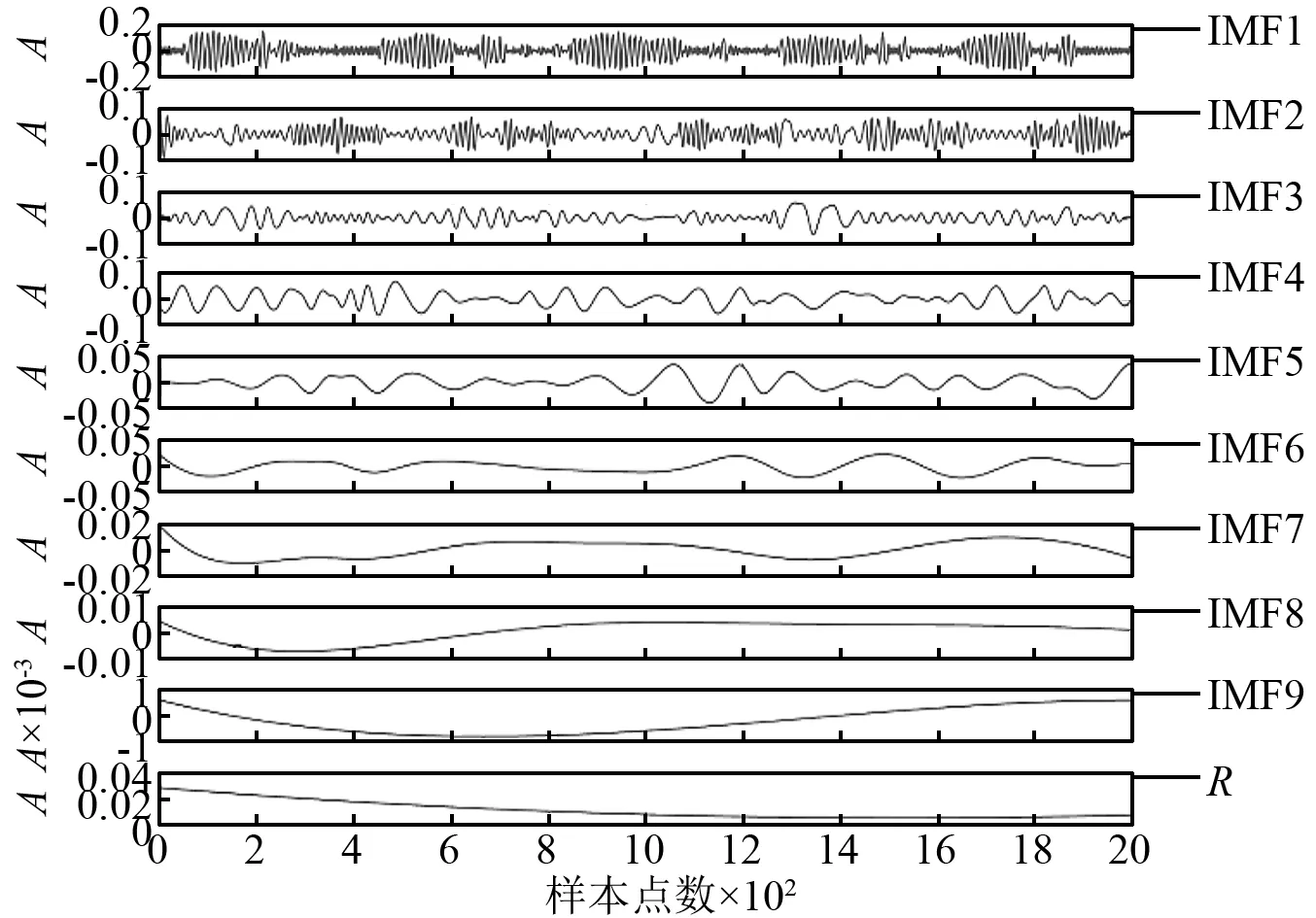
图4 正常信号EEMD分解波形图Fig.4 Decomposition waveform of normal signal

3.2.1 信号重构

由于噪声与原时序信号完全无关与无量纲参数：峭度K对信号的冲击成分比较敏感，因此可将IMF分量与原时序信号的相关系数与分量的峭度值作为IMF分量选择的指标。本文选取相关系数0.1作为筛选阈值，相关系数高于0.1的IMF分量保留下来，相关系数低于0.1的IMF分量移除。不同故障模式保留的IMF分量不尽相同，正常模式选择保留IMF1～IMF5，而OR017故障模式选择保留IMF1与IMF2。通过计算保留下来的IMF分量峭度值发现，内圈与外圈故障保留的IMF分量峭度值较高，且在故障直径上存在较大差异。选取峭度值较高的前两个IMF分量进行信号重构：正常状态选择IMF3与IMF5；b017与b053故障状态选择IMF1与IMF3；b035故障状态选择IMF1与IMF4；IR017，IR035，IR053，OR017与OR053故障状态选择IMF1和IMF2；OR035故障状态选择IMF3和IMF4。

3.2.2 故障特征提取

选择合适的故障特征是进行准确故障诊断的前提，通过EEMD的重构信号分析可以计算信号的特征参数，以此来判断轴承是否发生故障与发生故障的类型。在时域内分别选择三种有量纲参数：均值、标准差、均方根值与三种无量纲参数：偏度、峭度、裕度，见表1。

表1 三种有量纲与三种无量纲参数Tab.1 Three dimensional and three dimensionless parameters

3.3 参数设计

在模型参数设计之前，首先明确样本数据。样本数据的输入由故障特征提取的六种时域参数组成，每种故障状态下选择60组样本数据，正常状态下选择120组样本数据。样本数据的输出则由[0,…,0,1,0,…,0]T向量表示(1对应的位置i表示为第i种故障模式，其余为0)，正常、b017，b035，b053，IR017，IR035，IR053，OR017，OR035，OR053分别代表第1～第10种故障模式。同时将样本数据按照5∶1的比例进行随机分成训练数据与测试数据。

3.3.1 OHF Elman神经网络参数设计

OHF Elman神经网络算法的参数主要有精度指标与隐含层神经元数。参数确定过程与结果如下：

(1) 精度指标，选取均方误差MSE(mean square error)

(23)

式中：Ti为真实输出数据；Oi为网络输出数据；s为数据维度。

(2) 神经网络隐含层神经元数n的确定

根据式(24)首先确定隐含层神经元数在4～14。通过Elman神经网络在不同隐含层神经元数下进行训练，选择测试误差MSE较小的神经元数作为隐含层神经元数。如图5所示，隐含层数n确定为10。

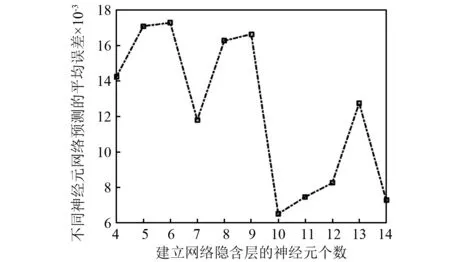
图5 神经元个数不同的Elman神经网络预测误差图Fig.5 Elman neural network prediction error graph with different number of neurons

(24)

式中：n为隐含层神经元数；r为输入层神经元数；m为输出层神经元数；a为1～10的常数。

3.3.2 OHF Elman-AdaBoost模型参数设计

根据OHF Elman-AdaBoost模型流程，OHF Elman-AdaBoost模型参数主要是阈值τ与弱回归器数量K，参数确定过程与结果如下：

(1) 阈值τ的确定

阈值τ的确定直接决定了样本的权重变化，从而决定了强回归器对样本的预测误差水平。为了确定阈值τ，首先选择弱回归器OHF Elman神经网络进行样本数据训练与测试，结果为：平均绝对误差为0.051 1，最大绝对误差为2，最小绝对误差为8.427 2×10-19，因此τ确定为0.01。

(2) 弱回归器数量K的确定

由于强回归器的诊断效果与弱回归器数量之间的相关性并不确定，弱回归器数量的增加甚至可能造成过拟合。考虑到集成学习的迭代时间和有效性，首先选择8～15作为弱回归器的数量范围，并分别进行OHF Elman-AdaBoost算法的测试训练，试验结果如图6所示。

为了选择弱回归器数量，以所有测试样本的MSE误差之和作为判别准则，如图6中的纵轴所示。图6说明了弱回归器数量对强回归器的影响是非线性的，并且在弱回归器数量为13时预测误差之和较小，因而确定弱回归器的数量K=13。

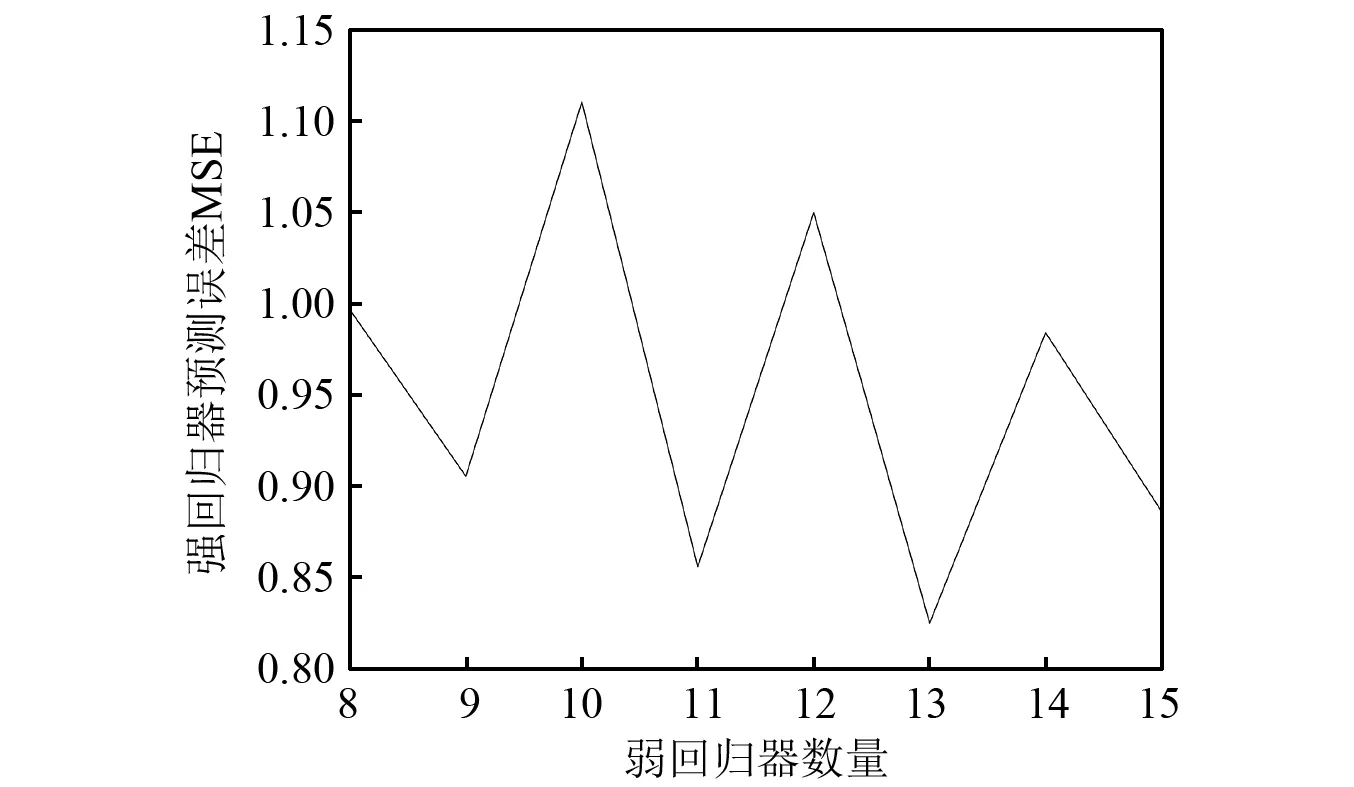
图6 不同数量弱回归器下的强回归器预测误差Fig.6 Prediction error of strong regressor under different numbers of weak regressors

3.4 模型训练

时小虎等学者在理论上证明了OHF Elman神经网络的收敛性与相较于Elman神经网络的优越性，但是这一结论还是需要进行实例验证。因此，本文在进行OHF Elman-AdaBoost模型的测试训练之前，首先进行Elman神经网络与OHF Elman神经网络的对比训练，其结果如图7所示。

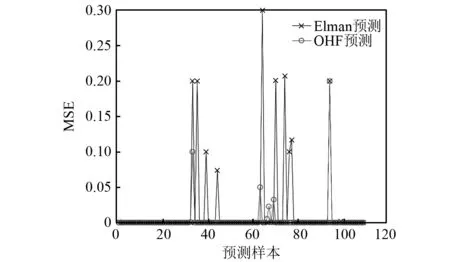
图7 Elman与OHF Elman神经网络预测误差图Fig.7 Prediction error of Elman and OHF Elman neural network

因为一组测试样本会得到一个10×1的绝对误差矩阵，将0.2作为误差数据的上限，10个误差结果均低于0.2为诊断正确，否则为诊断错误。根据诊断结果，Elman神经网络的诊断准确率为90.91%，OHF Elman神经网络的诊断准确率为91.82%。表2为OHF Elman神经网络的部分测试样本诊断结果。

表2 OHF Elman神经网络的部分测试样本诊断结果Tab.2 Diagnostic results of some test samples under OHF Elman neural network

图7是两种神经网络在各个测试样本上的诊断效果。可以看出，除去一组样本数据的预测误差上两种神经网络基本相同，在其他样本数据上的预测误差，OHF Elman神经网络皆小于Elman神经网络，证明OHF Elman神经网络的预测性能确实优于Elman神经网络。

在证明了OHF Elman神经网络更适合滚动轴承的故障诊断后，进行OHF Elman-AdaBoost的训练与测试，测试结果如图8与图9所示。

图8展示了每个弱回归器与强回归器对滚动轴承样本数据的平均诊断效果。如图8所示，强回归器的预测误差要远小于每一个弱回归器的预测误差。各个弱回归器的平均预测误差具体数据如表3所示。

表3 各个弱回归器的样本平均预测误差MSETab.3 Average of sample prediction error MSE for each weak regressor

图8 强回归器与各个弱回归器的预测误差对比图Fig.8 Comparison of prediction error between strong regressor and each weak regressor

图9展示了OHF Elman-AdaBoost算法得到的强回归器与OHF Elman神经网络弱回归器在各个测试样本上的预测误差效果。可以看出，除去在一组样本上强回归器与弱回归器预测误差几乎相等，强回归器基本上在所有测试样本上都取得了更好的预测效果。

图9 强、弱回归器在测试样本上的预测误差MSE对比图Fig.9 Comparison of prediction errors between strong and weak regressors on test samples

表4计算了表3中弱回归器的预测误差均值，并与强回归器预测误差进行了对比。结果可见，通过OHF Elman-AdaBoost算法得到的强回归器在弱回归器OHF Elman神经网络的基础上降低了61.7%的预测误差。

表4 强、弱回归器预测误差对比表Tab.4 Comparison of prediction error between strong and weak regressors

表5对比了所有弱回归器对于不同故障时期的平均预测误差与强回归器对于不同故障时期的预测误差，强回归器在不同故障时期的预测效果均优于弱回归器，其中在故障晚期预测效果提升最为明显，同时也在故障初期与故障中期上降低了约25%与66.5%的预测误差。在不同的故障部位上，强回归器也拥有较好的诊断效果，其中，对于内圈故障诊断效果最好，外圈故障次之，滚动体故障诊断误差最大。

表5 强、弱回归器下不同故障时期诊断预测误差对比图Tab.5 Comparison of prediction errors between strong regressor and weak regressor in different fault periods

表6则进一步细分对比了所有弱回归器对于不同故障不同时期的平均预测误差与强回归器对于不同故障不同时期的预测误差。如表所示，强回归器对于故障初期与故障中期的诊断误差主要集中于滚动体故障诊断，对于故障晚期诊断均具有非常好的效果。对于内圈故障的三种时期均具有较低的诊断误差，对于外圈的故障诊断误差主要来源于故障中期，而对于滚动体的故障初期与中期诊断效果较差。与弱回归器诊断结果相比，强回归器同时提高了在三种故障的不同时期诊断精度。由此可以验证，所提出的OHF Elman-AdaBoost算法在滚动轴承故障多时期诊断的精确性方面有着很好的性能优势。

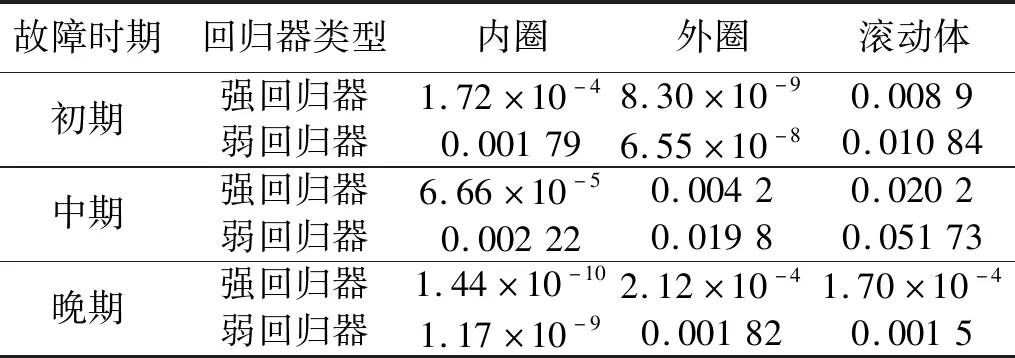
表6 强、弱回归器下三种故障的不同时期诊断预测误差对比图Tab.6 Comparison of prediction errors for different periods of three faults under strong regressor and weak regressor

4 结 论

针对滚动轴承不同故障时期故障信息的相似性与振动信号的非平稳性和非线性，本文提出了一种基于EEMD与OHF Elman-AdaBoost算法的研究框架。通过EEMD进行信号分解与重构，提取了有效的故障特征。然后选择OHF Elman神经网络作为滚动轴承故障诊断的主要方法，通过其独特的反馈结构，提高了对不同故障时期信息的动态处理功能。然后结合AdaBoost算法设计了一种新颖的OHF Elman-AdaBoost算法模型。经算例分析，OHF Elman-AdaBoost算法可以有效地对滚动轴承进行故障多时期诊断，同时提高了对全样本数据的预测精度。未来将进一步考虑优化神经网络结构与AdaBoost算法参数设计，以期在滚动轴承故障多时期诊断上提供更为精确的解决方案。