气液混输下侧流道泵内压力脉动特性研究

2021-03-31曹璞钰袁寿其洪秋虹

振动与冲击 2021年6期

陈轲，张帆，洪锋，曹璞钰，袁寿其，洪秋虹

(1.江苏大学国家水泵及系统工程技术研究中心，江苏镇江 212013；2.三峡大学机械与动力学院，湖北宜昌 443002；3.昆明嘉和科技股份有限公司，昆明 650000)

侧流道泵是一种新型超低比转速泵，其结构形式介于容积式泵和离心式泵之间[1]。侧流道泵具有小流量、高扬程和可自吸等特点，并且所有侧流道泵都具有一定的气液混输能力,部分多级侧流道产品甚至可以输送进口含气量高达50%的流体[2]。但由于侧流道泵内部流动复杂，侧流道和叶轮中流体受到了不同的离心力作用，在圆周运动同时又会产生纵向旋涡[3]，势必会产生较大的压力脉动，因此对气液混输下侧流道泵压力脉动特性研究是研发高性能侧流道泵的必要环节之一。

自20世纪20年代初，Siemen等[4]首次提出了侧流道泵的概念。随后，Schmiedchen等[5-7]基于Ritter的基础上继续对侧流道泵进行了深入研究，得到的理论沿用至今。进入21世纪，伴随着计算流体动力学(computational fluid dynamics，CFD)的快速发展，长期停滞的侧流道泵研究已经取得了很大进展。Fleder等[8-9]结合数值模拟和试验，通过修改几何参量，探寻侧流道泵水力性能变化规律。国内，Pei等[10-13]对侧流道泵内部流动形式、旋涡分布以及流动损失进行了详细研究分析，并通过试验探寻了不同叶片吸力角对侧流道泵气液混输能力的影响。总体看来，上述学者主要在纯水条件下对侧流道泵进行了水力性能优化设计研究，但对侧流道泵气液混输内部流动和不稳定流动机理缺少深入的研究，并且关于此内容的研究公开文献较少。

由于侧流道泵结构特殊、内部流动复杂，因而试验观测效果差，此外侧流道泵扬程极高，大部分侧流道泵无法进行安全可靠的可视化试验，而叶片泵常用的气液两相数值模型，如Mixture模型和Eulerian-Eulerian非均相流模型[14-20]无法准确适用于侧流道泵气液两相数值模拟。由于流动形式的区别，常规叶片式泵气液两相条件压力脉动规律[21-24]与侧流道泵也有一定区别。因此，尝试新的气液两相流数学模型，并对侧流道泵气液混输工况下压力脉动规律进行研究具有很高的经济意义和学术价值。

常用的气液两相数值模型基于离散相均一尺度的假设，假定处于流体中的气泡具有相同的直径。但实际上，由于气泡间或气泡与流体间的相互作用，气液两相流中的气泡还不断地有聚合与破碎现象的发生，产生多种尺寸大小不同的气泡[25]，在侧流道泵内复杂流动中作用更加明显。多气泡组质量传递(multi-size-group，MUSIG)模型通过将气泡按直径大小分为若干组，考虑了由于气泡聚合或破碎引起的气泡尺寸变化，具有较好的模拟精度[26-28]。目前尚未发现有在侧流道泵气液两相流动中的研究与应用。

本文首次应用MUSIG模型，对侧流道泵气液混输进行数值模拟，并对其内部压力脉动特性进行分析。

1 几何模型

侧流道泵核心水力部件为叶轮和侧流道，如图1所示。本文中选用叶片数z=24、吸力角θ=30°的开式叶轮，其他主要参数为：叶轮外径D2=150 mm，内径D1=80 mm，叶片宽度w=15 mm，轴向间隙σ与径向间隙s均为0.2 mm，间隙内径D0=50 mm；侧流道是1个截面为半圆的环形圆柱，其半径rc=35.2 mm；电机转速n=1 500 r/min。

图1 侧流道泵主要部件图Fig.1 The main components of a side channel pump

为了减少交界面设置，以降低计算偏差，计算水体中将轴向间隙和径向间隙并入叶轮水体，将出口管与侧流道并为一体，因此，整个侧流道泵水体主要分为3个部分，如图2所示。

图2 侧流道泵水体图Fig.2 The entire water domain of a side channel pump

2 数值模拟

2.1 网格划分

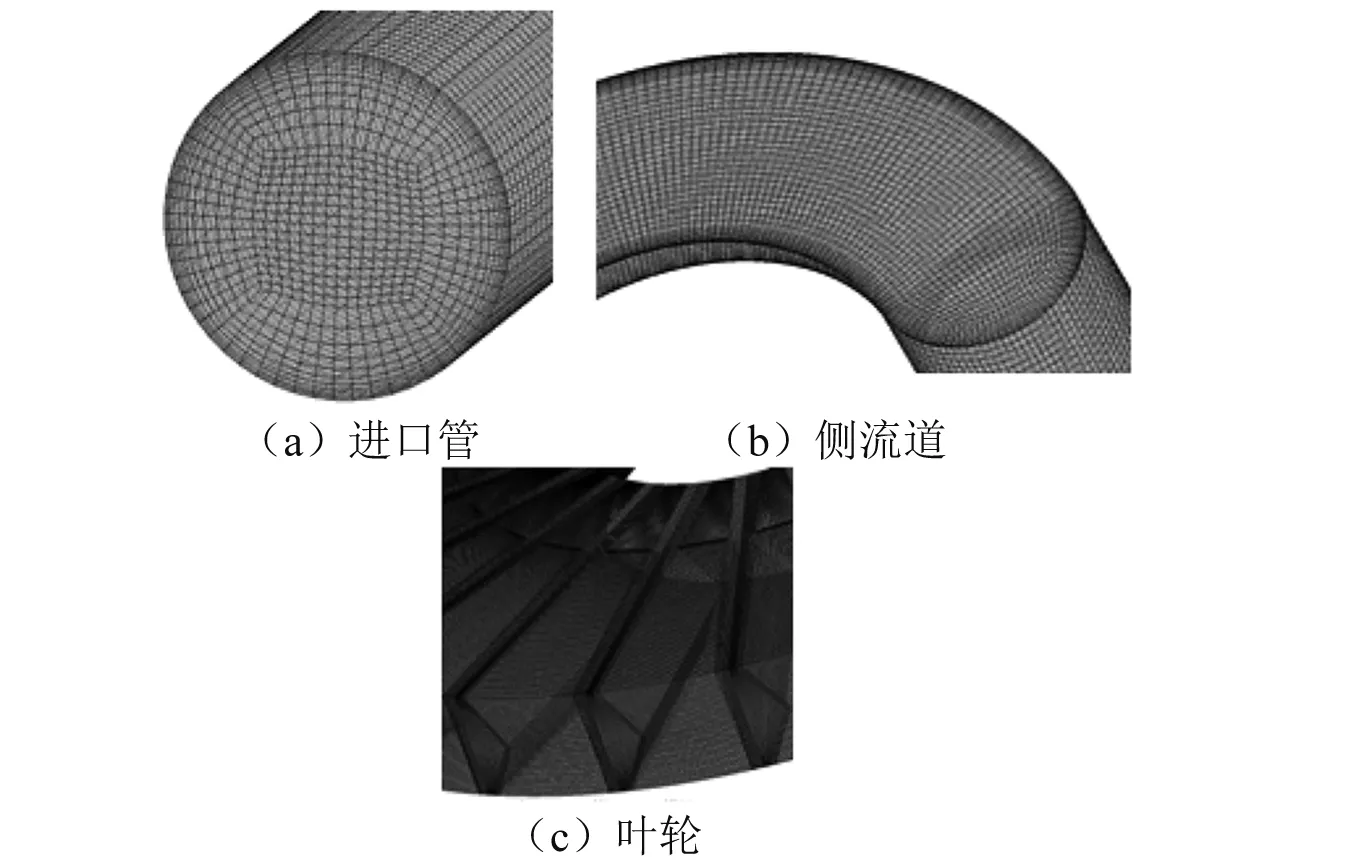
图3 侧流道泵计算网格Fig.3 Detailed mesh view

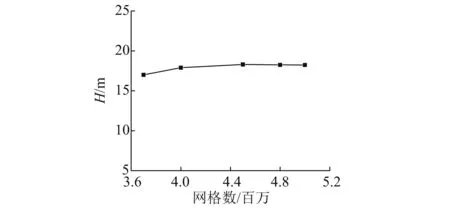
图4 网格无关性Fig.4 Mesh independence

表1 主要流域网格参数Tab.1 The grid quality

2.2 MUSIG模型

MUSIG模型是一种描述多相流体系中离散相大小与分布随时空变化的通用模型，能够描述离散相实体的分布特性以及引起分布变化的离散相微观行为。MUSIG模型的核心是群体平衡方程[29]，如式(1)所示

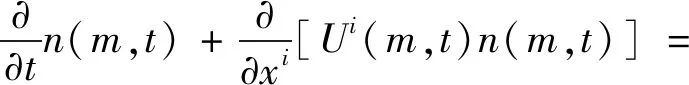
(1)

式中：等式左边n(m,t)为在时间t内质量粒子的密度；等式右边BB,DB,BC,DC分别为气泡破碎所形成的新的气泡出生率、气泡破碎所导致的原气泡死亡率、气泡凝聚所形成的新的气泡出生率、气泡凝聚所导致的原气泡死亡率，其表达式分别为

(2)

(3)

(4)

(5)

式中：g(m;ε)为质量粒子m破碎为ε和m-ε的破碎速度；Q(m;ε)为质量粒子聚并为ε和m+ε时的聚并速度。

2.3 计算设置

利用软件ANSYS CFX 17.0来求解基于质量守恒定律的不可压缩流体连续性方程和RANS方程，湍流模型选用SST模型；设置质量流量进口，出口压力设置为101.325 kPa；综合考虑侧流道泵结构参数，气泡直径设为0.1～3.0 mm，分为5组[30-32]；交界面设为counter rotating wall以减小间隙并入叶轮水体的影响，收敛精度设为10-5。

非稳态计算基于稳态计算结果，每旋转1°作为1个时间步长，电机转速n=1500 r/min，因此，时间步长Δt=1.11×10-4s，叶轮一共旋转4圈，总时间t=0.16 s，取稳定后最后一圈结果进行分析。

在叶轮内有代表性位置设置监测点，如图5所示。以叶轮进口处旋转角度为0°时设立监测点A1，在旋转角度分别为60°，150°，240°，300°和330°时设立监测点A2，A3，A4，A5，A6，各旋转角度自叶轮内缘至外缘等距离设置6个监测点，监测点所处半径r分别为42 mm，48 mm，54 mm，60 mm，66 mm和72 mm时分别为Im1，Im2，Im3，Im4，Im5，Im6。

图5 监测点Fig.5 Monitor points

3 计算结果

3.1 水力性能分析

为了探究单级侧流道泵气液两相流动规律，因此，统一侧流道泵在单相与气液混输工况流动中的流量及性能，定义流量系数Ф与扬程系数ψ，如式(6)和式(7)所示。试验台如图6所示。试验结果如图7所示。

图6 试验台示意图Fig.6 Schematic diagram of test rig

图7 扬程试验结果Fig.7 The result of test hydraulic head

(6)

(7)

式中：Ql为液体流量，m3/s；Qg为气体流量，m3/s；u2为出口圆周速度，m/s；Δptot为进出口总压差，Pa。

将额定流量下进口含气率(inlet gas volume fraction，IGVF)为0%，2%，4%和6%时单级侧流道泵气液混输模拟结果后处理得到的扬程系数曲线，如图8所示。由图8可知，通气状态下模拟值大于试验值，但模拟总体趋势与试验结果相似，随进口含气率增加扬程逐渐减小。试验扬程在进口含气率从0%提升到2%时陡降，这是由于侧流道泵抗汽蚀能力差，少量通气，极易发生汽蚀导致性能陡降[33]，这也是气液混输工况下模拟值偏低的原因之一。

图8 不同进口含气率下试验与模拟扬程对比Fig.8 Hydraulic head of test and simulation under different IGVFs

同时可以发现：当进口含气率由2%提升到4%时，模拟扬程系数降低0.384，试验扬程系数降低0.43；当含气率由4%提升到6%时，模拟扬程系数降低0.22，试验扬程系数降低0.167，差值接近。结果证明，MUSIG模型适用于侧流道泵气液混输模拟计算。

3.2 气泡直径变化

MUSIG模型将气泡按直径大小分为若干组，考虑了由于气泡聚合或破碎引起的气泡尺寸变化，再采用所谓群体平衡原理量化各组内气泡数量。以叶轮中间截面圆心为原点设置3个截面，如图9所示。其中，P1,P2和P3在XY面上且Z方向位置分别为z1=-7.6 mm,z2=0,z3=7.6 mm。

图9 截面设置Fig.9 Section setting

大直径气泡主要聚集于侧流道泵的进口段处，除进口段以外的其余部分气泡直径相对进口段明显较小，并且变化幅度不大，如图10所示。而常规离心式叶轮通气时，气泡汇聚并形成大直径气泡，严重时将堵塞流道，而侧流道泵由于叶轮流道内强剪切流导致无法形成大直径气泡，气泡会迅速破碎，这与通常气泡流形式不同，这也是几乎所有侧流道泵都具有一定气液混输能力的原因。而叶轮与侧流道交界的轴向间隙的内缘处会聚集大直径气泡，尤其是中段至出口段之间的轴向间隙处气泡直径明显大于其他部位。

图10 气泡直径在各截面上分布图Fig.10 The diameter distribution of bubbles on different sections

3.3 流线分布

单相和气液两相在扬程最大值工况时在叶轮各截面上的流线图，如图11所示。由图11可知，在各截面上单相时旋涡的强度与旋涡数量明显大于气液两相工况下，尤其是在间隙处，单相工况下旋涡强度较大。在监测点所在P2面上，可以发现进口段强旋涡强度降低，而出口段旋涡在通气后旋涡明显减小甚至消失，因此少量通气有助于改善侧流道泵流态。

图11 液相流线在各截面上分布图Fig.11 The streamlines distribution on different sections

3.4 压力波动强度特性研究

3.4.1 压力波动强度分布

为了计算整个旋转周期内所有节点的整体压力波动强度，定义压力波动强度系数Cp*，如式(8)所示，该式可以反映1个周期内，叶轮内每个网格节点压力波动强度。

(8)

式中：ς为网格节点；N为一个旋转周期内压力p的采样次数；t0为旋转初时刻；j为时间步数。

侧流道泵在纯水工况下和进口含气率为2%时，气液两相流动下全流域压力波动强度对比图，如图12所示。由图12可知，叶轮流域靠近进口侧相对于靠近侧流道侧压力波动强度较大，这是由于靠近进口侧除进口管外均为平壁面，且壁面间隙仅为0.2 mm，这种结构必然会阻碍离心力作用下的各方向旋涡的运动，狭窄的流动空间无法使近壁面处旋涡无阻碍运动，随之而来大量的液流必定会冲击壁面，造成此处压力波动强度高于靠近侧流道的叶轮流域。

图12 全流域压力波动强度分布Fig.12 Pressure fluctuation intensity distribution in entire flow domain

当进口含气率为2%时，压力波动强度有所减小，原因是少量的气体进入叶轮后，一定程度上降低了压力脉动的波动幅度。而侧流道内整体压力波动强度在单相和气液混输工况时近似且明显小于叶轮内压力波动强度，这是由于弧形侧流道具有充分的流动空间，可以使旋涡从叶轮流出后在侧流道内充分衍化，减少了由于流动空间不足而导致流体与壁面之间的冲击。

为了更确切地显示叶轮内部压力脉动，选取P1,P2 和P3，如图13所示。由图13可知，叶轮外缘处的压力波动强度往往大于该叶轮内缘处。由于P3是叶轮与侧流道之间的交界，可以发现在如图13(c)所示的叶轮半径位置出现明显的压力波动高强度区，这是因为流体受到从叶轮进入侧流道和从侧流道中返回至叶轮过程中的交换作用，此处为流体进出流道交汇区域，因此具有较高的压力波动强度，因而也出现了所示的狭长高压力波动强度区域。

图13 单相流动下叶轮内压力波动强度分布Fig.13 Pressure fluctuation intensity distribution in impeller under single-phase flow

气液两相流动时各截面压力波动强度，相较于单相时，进口含气率为2%的气液两相工况下侧流道泵叶轮内部压力波动强度较低，整体变化规律与单相时近似，如图14所示。但在位于侧流道泵进口处靠近侧流道的轴向间隙内径处，出现一段系数高达130的高压力波动强度区，较叶轮内其他区域强度系数高近百倍，这也是侧流道泵气液混输工况下易发生振动的主要原因。

图14 两相流动下叶轮内压力波动强度分布Fig.14 Pressure fluctuation intensity distribution in impeller under two-phase flow

3.4.2 压力脉动时域分析

不同旋转角度下由叶片外缘至内缘各监测点压力脉动时域图，如图15所示。单相状态下，同角度，外缘处压力通常大于内缘处，压力极大值总出现在外缘处，极小值总出现在内缘处，这是由于叶轮内流体往往由外缘处流出叶轮进入侧流道，由内缘处从侧流道流入叶轮，因此同一旋转角度，外缘处流体比内缘处流体多进行一次叶片机械能转化为压力势能的过程。在叶轮内任何监测点1个旋转周期内压力脉动总会出现18个规则的周期性波动、2个过渡阶段波动以及4个不稳定的振荡式波动，这是由于侧流道泵进出口之间存在1个中断位置，以隔开进口低压区和出口高压区，减小高低压区域之间的干扰。因此当叶片旋转时，在中断位置会恒定有两枚叶片加上完全在进出口的两枚叶片，总计有4枚处于特殊位置的叶片，与4个不稳定振荡式波动相对应。在不稳定振荡式波动前后各有1个过渡阶段，分别为即将离开进口和进入出口的叶片各一枚，与周期性波动和振荡式波动形式都有区别，因此命名为过渡阶段波动。不稳定振荡式波动和过渡阶段波动是侧流道泵与普通叶片式离心泵主要区别之一。

图15 单相时叶轮内各监测点压力脉动时域图Fig.15 Time domain characteristics of pressure pulsation at each monitoring point in the impeller under single phase

侧流道泵气液两相流动下时域图，如图16所示。IGVF为2%工况下规则周期脉动及不稳定振荡式波动发生时经过的时间步长与单相工况下相同，各周期压力峰值略小于单相工况下而压力谷值相较单相则偏大。

图16 气液两相时叶轮内各监测点压力脉动时域图Fig.16 Time domain characteristics of pressure pulsation at each monitoring point in the impeller under two-phase flow

侧流道内各监测点压力脉动对比，与叶轮相比，侧流道内各监测点无论是单相还是气液两相流动下都具有24个规律性的压力脉动周期，如图17所示。由进口至出口，流体的压力逐渐增加。与叶轮内不同，单相工况下侧流道内各监测点压力谷值于气液两相时近似相等，但峰值单相较气液两相时大。

图17 单相与气液两相时侧流道内各监测点压力脉动时域图Fig.17 Time domain characteristics of pressure pulsation at each monitoring point in the side channel under single phase and two-phase flow

3.4.3 压力脉动频域分析

对最后1个周期各监测点压力脉动时域值进行快速傅里叶变换，得到压力脉动频域值。

各监测点的主要频域特性近似，压力脉动激振频率主要发生在600 Hz(24×fn)，1 200(48×fn)，1 800(72×fn)等频率，压力脉动峰值主要出现在轴频的整数倍处，也是侧流道泵叶片数的整数倍，如图18所示。叶轮上全部36个监测点主频相同，且在主频上压力脉动幅值基本相同，这说明侧流道泵叶轮内压力脉动主要受到流体在叶轮域侧流道之间的交换流动作用影响，这与常规离心式叶片泵由于叶轮与蜗壳之间动静干涉压力脉动幅值变化较大的结论不同。

图18 单相时叶轮内各监测点压力脉动频域图Fig.18 Frequency domain characteristics of pressure pulsation at each monitoring point in the impeller under single phase

当进口通气时，与单相时近似，如图19所示。压力脉动激振频率主要也发生在轴频的整数倍处，证明了侧流道泵主频与通气量无关，而与叶片数有关。而相较于单相，IGVF为2%的情况下，主频及次频的压力脉动幅值明显较小，与上述压力波动强度分布对应。

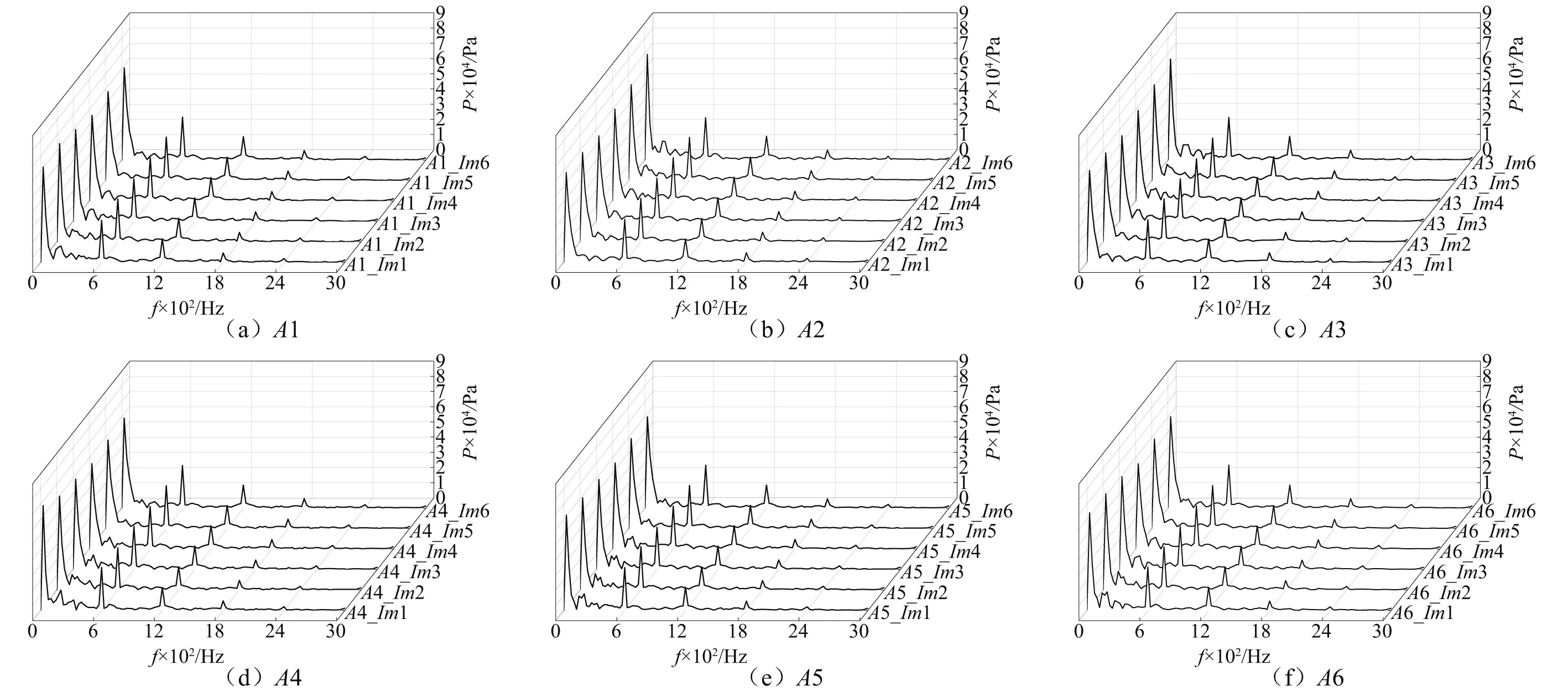
图19 气液两相时叶轮内各监测点压力脉动频域图Fig.19 Frequency domain characteristics of pressure pulsation at each monitoring point in the impeller under two-phase flow

侧流道泵单相和气液两相流动时侧流道内监测点的压力脉动频域图，如图20所示。与叶轮内监测点相同，侧流道内压力脉动的主频也发生在600 Hz(24×fn)，1 200(48×fn)，1 800(72×fn)等频率。气液混输工况下，侧流道主频及次频的压力脉动幅值相对于单相小，与叶轮内情况相同。此外，在进口所在旋转0°的监测点，其主频及次频的压力脉动幅值明显小于其他位置，与上文所述原因一致，初始位置流动刚开始由规则状态进入螺旋运动状态，旋涡没有充分衍化，此时压力脉动受叶轮与侧流道中交换流影响较小。

图20 单相与气液两相时侧流道内各监测点压力脉动频域图Fig.20 Frequency domain characteristics of pressure pulsation at each monitoring point in the side channel under single phase and two-phase flow