一种准零刚度车载隔振系统的设计与试验研究
2021-03-31李韶华冯桂珍
赵 权,李韶华,冯桂珍
(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043;2.石家庄铁道大学 机械工程学院,石家庄 050043)
军用特种车辆行驶工况复杂、环境条件恶劣,车载精密仪器会受到振动等多个干扰源的影响,会产生较大的振动加速度和振幅,严重时会对精密仪器设备造成损害。为了减小由于振动对车载精密仪器的磨损,减振器得到了广泛的应用和发展。
由于车体本身具有一定的减振功能,再并联上传统隔振系统的隔振效果,对于20~200 Hz内的振动能有很好的隔离[1]。同时,由于车内空间限制,减振系统应尽量体积轻便,便于安装。
近年来国内外学者对准零刚度系统进行了大量的研究,准零刚度隔振系统是在正刚度弹元件基础上并联负刚度机构,负刚度机构用于刚度校正,使隔振系统在承载力不变的情况下总刚度减小,固有频率降低[2-4]。Carrella等[5]提出的经典三弹簧结构,其基本原理就是用两条倾斜的弹簧产生负刚度,抵消竖直弹簧的正刚度,被隔振物体的质量由竖直弹簧支撑。孟令帅[6]和Niu等[7-8]分别采用变厚度碟形弹簧和开槽碟簧作为负刚度元件设计了正负刚度并联的隔振器,并通过理论分析与试验验证研究了系统的低频隔振性能。杜宁等[9]针对车载光电设备低频振动,设计一种新型准零刚度隔振系统,并对其振动响应进行了模态仿真及性能测试,验证了系统的隔振有效性。王勇等[10-11]将立方速度反馈控制、时滞立方位移反馈策略引入到准零刚度隔振器的主动控制中,有效的提高了准零刚度隔振系统的隔振特性。邵栋等[12]运用谐波平衡法分析系统强非线性振动的功率流,探讨非线性刚度和非线性阻尼对隔振系统功率流的影响,并验证其隔振有效性。赵艳影等[13]采用多尺度法研究了时滞非线性动力吸振器对主系统的减振性能,以及反馈增益系数对时滞控制主系统的振动的影响。传统的车载隔振系统存在空间占比大、结构复杂、安装困难、低频隔振效果不理想等问题。为了提高车载隔振系统的低频隔振性能,且能达到良好的控制效果。本文首先设计了一种空间占比小、结构简单且安装方便的准零刚度隔振器,可安装在车体较小空间内。通过理论分析和装配零件实测数据分析确定了系统在平衡位置处系统的参数。通过低频段小振幅简谐位移激励工况试验结果分析得到,设计的准零刚度车载隔振系统在0~4 Hz低频段,在降低系统固有频率的同时保持良好的隔振性能。车载随机激励工况仿真结果表明,准零刚度隔振系统稳定性较好,具有良好的隔振性能。
1 准零刚度隔振系统静力学分析
如图1所示为自行设计的准零刚度隔振器,由斜置弹簧作为负刚度调节机构与正刚度弹性元件并联组成。图示虚线位置为系统受载后,系统达到静平衡状态。m为承载质量;kv,kh分别为垂向弹簧与斜置弹簧刚度;L为斜置弹簧初始长度,l为其位于水平位置时的长度;y为承载质量位移;q为系统受到的简谐激励位移;cv为垂向阻尼阻尼系数,斜置弹簧安装会有摩擦,考虑到阻尼力,设其阻尼系数为ch。
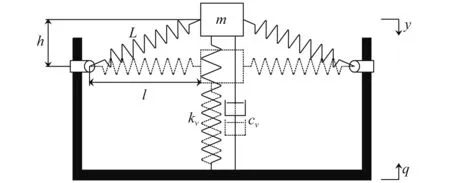
图1 准零刚度隔振器结构示意图Fig.1 Structure diagram of quasi-zero-stiffness vibration isolator
对系统进行静力学分析时,不考虑质量m、垂向阻尼和斜置阻尼的影响,产生的弹簧力为垂向弹簧和斜置弹簧产生的弹性力的矢量和,准零刚度隔器的弹性力及刚度表达式为
(1)
进行变换坐标,令x=y-h,则式(1)变为
(2)
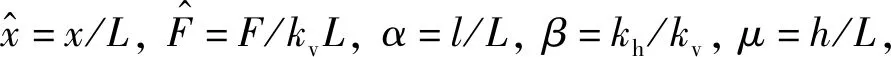
α2+μ2=1
(3)
得到式(2)无量纲化关系式为
(4)
对式(4)求导,可得到其无量纲刚度表达式
(5)
式中:β为垂向与斜置弹簧的刚度比;α为斜置弹簧位于水平位置时的压缩比。
由式(4)和式(5)可以得到准零刚度隔振系统的无量纲力-位移、刚度-位移曲线,如图2所示。
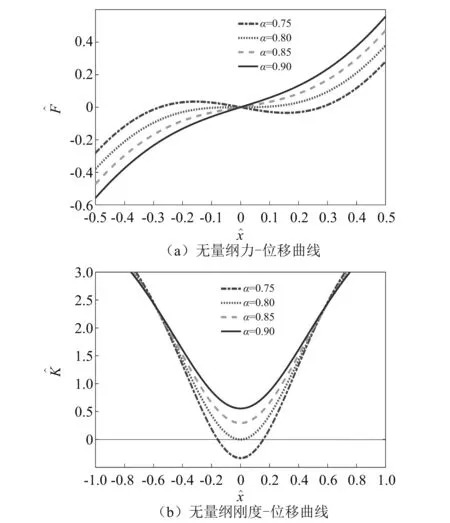
图2 无量纲力-位移和刚度-位移曲线Fig.2 Dimensionless force-displacement and stiffness-displacement curves
图2中可看出,系统刚度特性随着α的递增,系统刚度越大,当α=αqzs=0.8,系统在静平衡位置处斜置弹簧产生的负刚度与垂向弹簧产生的正刚度相互抵消,并且在一定的位移量内,可获得准零刚度特性;当α≤αqzs=0.8时,系统在静平衡位置附近处的刚度为负值;当0.8=αqzs≤α≤1时,系统刚度为正值。α越小表示斜置弹簧预紧程度越高,提供给系统的负刚度也越强,系统表现出的非线性特征越明显。
由图3所示,当β>4时,位移-力的曲线斜率小于等于0,系统在一定范围内存在负刚度。当β=4时,与图2中α=αqzs=0.8的曲线相同,系统处于静平衡位置的无量纲刚度为零,恰好处于准零刚度状态。当β<4时,系统的刚度为正值。结合图2,当β=4时准零刚度隔振系统在静平衡位置附近小振幅范围内具有低动刚度特性。实际工程中很难达到负刚度,β取值应满足1≤β<4。
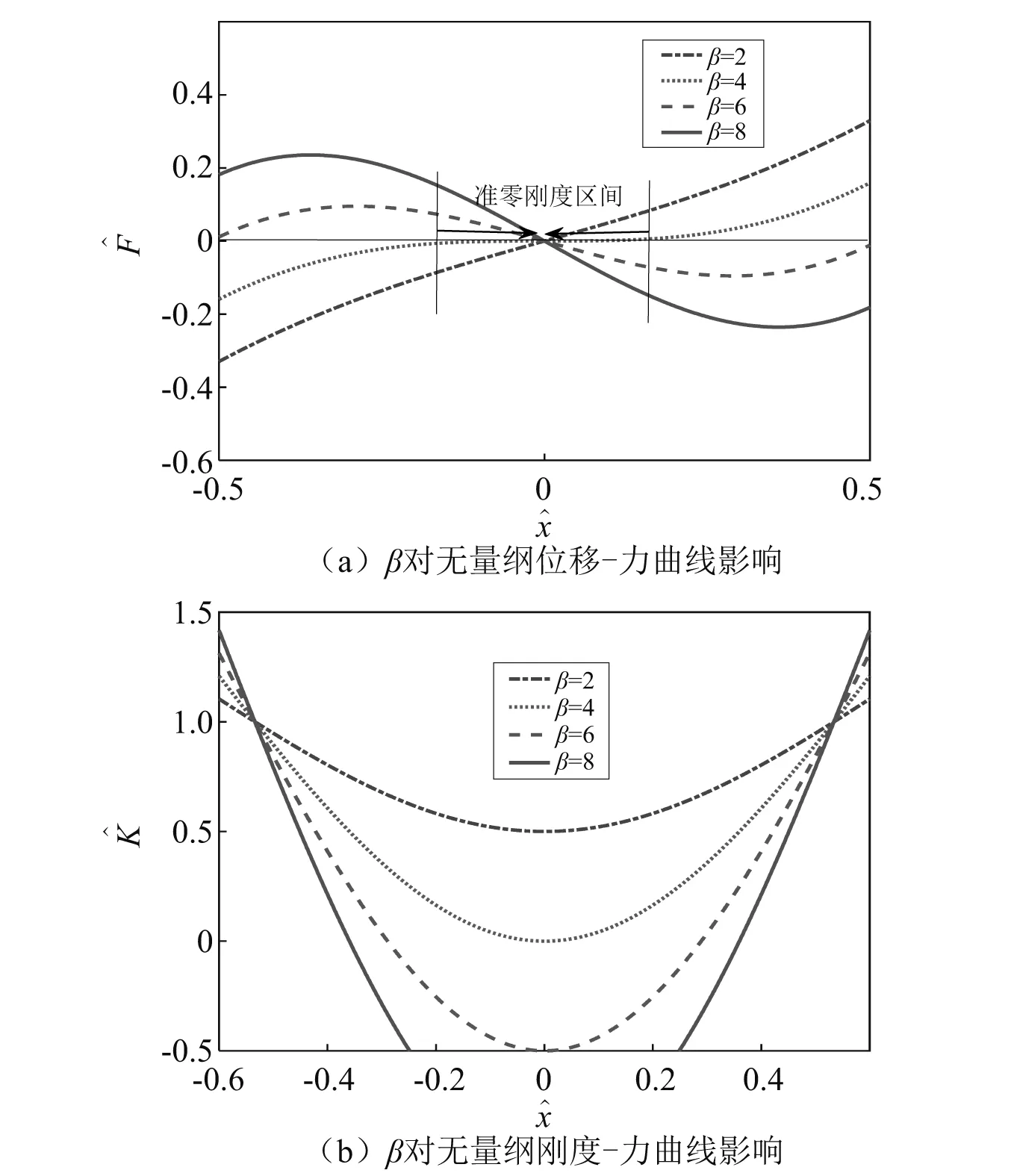
图3 β对无量纲位移-力和刚度-力曲线影响Fig.3 Influence of β on displacement-force and dimensionless stiffness-force curves
2 刚度特性分析
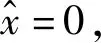
(6)
由式(6)可以求得系统使平衡位置满足无量纲刚度为零的参数条件为
(7)
式中,下标qzs为使静平衡位置处的满足等式(6)的无量纲参数值。理论上,如果系统在静平衡位置刚度越接近零则能够隔离外界的最低频率也接近零,可以实现低频甚至超低频隔振。而实际工程应用中考虑到加工、安装误差等因素影响,且负刚度具有不稳定性,因此在设计正负刚度弹簧并联结构时,必须避免出现负刚度,且保证系统刚度为大于零的正值。综上,在进行正负刚度弹簧并联系统设计时,无量纲参数α,β应为α=(1+ε)αqzs或β=(1+ε)βqzs,其中ε为加工误差系数,取为加工误差对系统参数影响的百分比。
设β=(1+ε)βqzs,且β>βqzs,代入式(5),得到无量纲刚度表达式
(8)
同理,设α=(1+ε)αqzs,α>αqzs,代入式(5)得到无量纲刚度表达式
(9)
在静态平衡位置处的刚度值为
(10)
根据式(8),取α=0.8,对加工误差系数ε进行不同赋值,得到无量纲位移刚度曲线,如图4(a)所示。根据式(9),取β=2,改变ε取值,也可得到无量纲位移刚度曲线,如图4(b)所示。由图分析得,当ε=0时,无量纲刚度在静平衡位置处的刚度值为零;随着加工误差系数ε的增大,在静平衡位置处的无量纲刚度值也随着增大且等于ε的改变量。加工误差直接影响着系统在静平衡位置处的刚度值。因此,在实际装置的设计加工中,应综合考虑加工难度、经济性等因素,保证尽量小的加工误差。
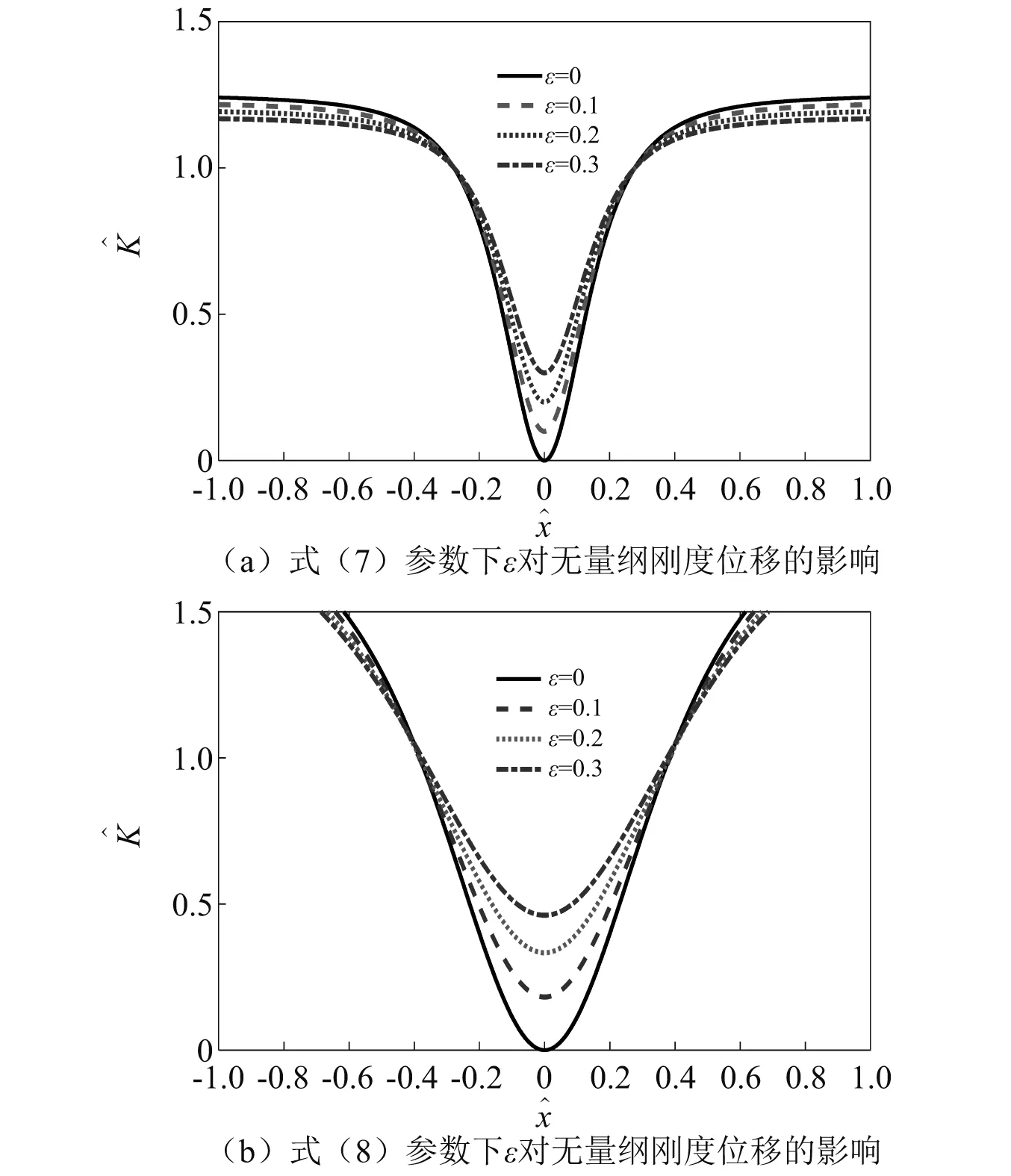
图4 式(7)和式(8)参数下ε对无量纲刚度位移的影响Fig.4 Influence of ε on dimensionless stiffness-displacement under formula (7) and formula (8) parameters
综上分析,通过改变ε的大小,合理设计参数α=(1+ε)αqzs或β=(1-ε)βqzs,正负刚度弹簧并联机构刚度比在1≤β<4区间取值较好,对应压缩比的取值范围为0.5≤α<0.8,可控制正负刚度并联系统的静平衡位置处的刚度值,从而得到准零刚度系统。
3 简谐位移激励下系统非线性动力学分析
考虑到车载仪器工作性能会受到外界干扰引起的振动的影响,研究准零刚度隔振系统在简谐位移激励下的微分方程。如图1所示,系统承载质量为m的被隔振物体,受到重力作用,垂向弹簧和斜置弹簧会受到压缩,最终达到静态平衡位置,且满足准零刚度特性。对其施加简谐位移激励q=Acos(ωt),被隔振物体m的绝对位移为X,并且考虑到负刚度机构阻尼,得到系统的非线性振动微分方程
(11)
式中:m为承载质量;L为斜置弹簧初始长度;l为斜置弹簧在水平位置长度;kv为垂向弹簧刚度;kh为水平弹簧刚度;cv为垂向阻尼器阻尼;ch为负刚度机构阻尼。
对式(11)进行无量纲化可得
(12)
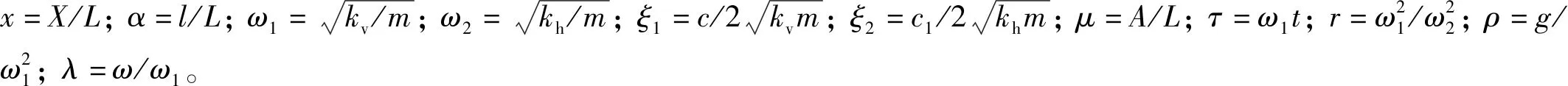
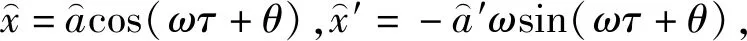

(13)
将所设的周期解和(13)式代入式(12)得到
(14)
其中,
设ωτ+θ=φ,对式(14)在(0~2π)周期内平均化处理
(15)
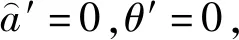
(16)
其中,
(17)
式(16)消去三角函数项可得
(18)
整理式(18)可得准零刚度隔振系统稳态幅频响应解析表达式
(19)
(20)
其中,
当准零刚度隔振系统受简谐位移激励时,稳态幅频响应为
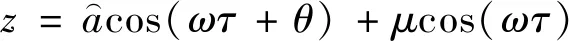
(21)
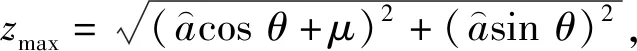
(22)
准零刚度隔振系统去除负刚度机构,系统变为准零刚度隔振系统对应的线性隔振系统,在相同的简谐激励下的位移传递率为
(23)
式中,λ为激励频率与线性隔振系统固有频率之比。
4 系统参数对隔振性能影响
综上分析,对于在简谐位移激励下的准零刚度隔振系统,由式(21)的系统稳态幅频响应关系,图5(a)所示为激励幅值μ和垂向、斜置阻尼比ξ1,ξ2一定,系统的响应峰值随着压缩比α递增而增加,同时共振频率向右移动,同时系统的向上跳跃起始频率、向下跳跃起始频率均增大,且系统的共振频率随着α增大而增大。随着频率的增大,系统的稳态响应幅值变化缓慢,趋于稳定。图5(b)为其他参数一定,改变激励幅值大小,研究不同激励幅值对系统幅频响应曲线的影响,随着μ的增大,曲线的骨架线保持不变,系统的幅频响应峰值和共振频率均增大,μ的变化会影响系统起始幅值,低频段对系统的幅值影响明显,高频段影响不大,总体而言,激励幅值较小时,准零刚度隔振系统的隔振效果表现得更明显。
图5(c)和图5(d)分别为其他参数一定,改变垂向阻尼比ξ1和斜置阻尼比ξ2大小,研究其对幅频响应曲线影响,在整个频率区间上随着垂向、斜置阻尼比增大,响应峰值和共振频率均减小,共振支也得到有效抑制,且系统表现得非线性也越弱,低频段垂向阻尼对系统幅频响应影响不大,高频段随着垂向阻尼的增大系统稳态响应幅值会随着增大,而斜置阻尼的变化在整个频段范围内对系统稳态响应幅值的影响不大。因此,适当增大垂向阻尼,有利于降低系统稳态响应幅值,提高系统的隔振性能。

图5 不同参数对系统幅频响应曲线的影响Fig.5 Influence of different parameters on amplitude frequency response curves
由图6所示,为不同垂向、斜置阻尼比和不同激励幅值下的准零刚度隔振系统位移传递率曲线与对应线性系统的传递率曲线的对比。设ξ1+ξ2=ξ,由图6(a)和图6(b)可以看出,随着阻尼比的增大准零刚度隔振系统位移传递率的共振峰值减小,隔振频带变宽,跳跃现象得到抑制。由图6(c)可以看出,随着激励幅值逐渐增大,准零刚度隔振系统的共振峰处的幅值增大,系统发生跳跃现象越来越明显,并且系统的起始隔振频率也越大。虽然共振峰值小于线性系统,可随着阻尼比越小、激励幅值越大系统表现的非线性越较为明显,且位移传递率的共振峰值越大,则可能会导致准零刚度隔振系统比线性隔振系统效果差。综上分析,系统对小位移激励的隔振效果更好。

图6 不同阻尼比和激励幅值对位移传递率影响Fig.6 Influence of different damping ratio and excitation amplitude on displacement transfer rate
5 准零刚度隔振系统试验与结果分析
5.1 隔振器实验参数设计
考虑到负载试验时弹簧需要有很好的弹性形变能力和稳定的力学性能,选择常用的60Si2Mn弹簧钢,切变模量G=79 000 N/mm2,制作成圆柱螺旋压缩式弹簧。
设定静载质量为9 kg,垂向弹簧在静载作用下的压缩形变量h=0.09 m,由mg=kvh,得到垂向弹簧刚度为kv=980 N/m,根据机械设计手册中的弹簧设计准则,选取弹簧丝径d=4 mm,中径D=65 mm,有效圈n=8,由弹簧刚度计算公式
(24)
求得kv=1 040 N/m,利用拉压弹簧刚度测试仪测得实际垂向弹簧刚度为kv=1 017 N/m,根据静载受力平衡条件,将静载质量修正为9.2 kg。
由于负刚度只在理论上出现,实际系统的刚度只能为接近于零的正值,由式(7)准零刚度条件及误差系数分析,设垂向弹簧与斜置弹簧的刚度比为1/2,选取弹簧丝径d=2.8 mm,中径D=42 mm,有效圈n=7.5,由式(24)计算得到每根倾斜弹簧的刚度为1 085 N/m,实测值为1 010 N/m。为保证平衡位置斜置簧处于水平状态,需满足L2=l2+h2,得L=0.121 m,l=0.081 m。

表1 试验模型的物理参数Tab.1 Physical parameters of the test model
5.2 试验装置及技术条件
课题组自行研制的准零刚度隔振系统,如图7所示。试验系统及原理图如图8、图9所示。具体包括以下三个部分:

图9 试验系统示意图Fig.9 Schematic diagram of test system
(1) 准零刚度隔振系统试验装置。该部分由课题组自行研制。主要包括——承载质量块、弹簧(一个垂向弹簧、两个斜置弹簧)、垂向弹簧定位导杆、套筒结构,压缩量调节装置。其中定位导杆为垂向弹簧导向,防止弹簧振动时产生弯扭,保证垂向的刚度。压缩量调节装置可以调节垂向弹簧与斜置弹簧的压缩量,保证隔振器的初始位置处于水平状态。套筒结构是为了避免隔振器在振动过程中产生碰撞,其各部件均用机油润滑,以尽量减小摩擦和阻尼。
(2) 激振系统。采用澳大利亚卧龙岗大学与合肥工业大学联合研发的六自由度振动试验台,主要由NI控制系统、PC端电脑控制器、DMKE电动缸等组成。参数范围为沿xyz轴移动,速度v<200 mm/s,加速度a<3 000 mm/s2;绕xyz轴向转动,角速度v<70 °/s,角加速度a<300 °/s2。
(3) 数据采集。Keyence LK-G500激光位移传感器、数据采集仪(型号:INV306U),通过DASP软件采集实时波形、并对数据进行保存及处理。

1-垂向弹簧;2-限位调节结构;3-承载质量块;4-垂向导杆;5-斜置弹簧和套筒结构。图7 准零刚度隔振器实验装置Fig.7 Experimental equipment of quasi zero stiffness vibration isolator

1-振动台控制电脑;2-数据采集电脑;3-采集仪;4-振动台;5-准零刚度隔振系统;6-激光位移计。图8 振动试验现场及实验设备Fig.8 Vibration test site and equipment
5.3 简谐激励工况试验与结果分析
研究准零刚度隔振系统在简谐位移激励下的隔振特性。选取激励振幅分别为3 mm,5 mm,7 mm,依次对隔振器Z轴方向进行正弦激励试验。
在满足振动台参数设定要求的情况下,设定振动台的频率范围为0.5~4.0 Hz,信号采集仪的采样频率设置为1 024 Hz,应用 DASP 软件的数据采集功能记录受试质量块的实时位移数据,通过时域分析和频域分析功能对采集到的数据进行初步处理。试验参数见表2。
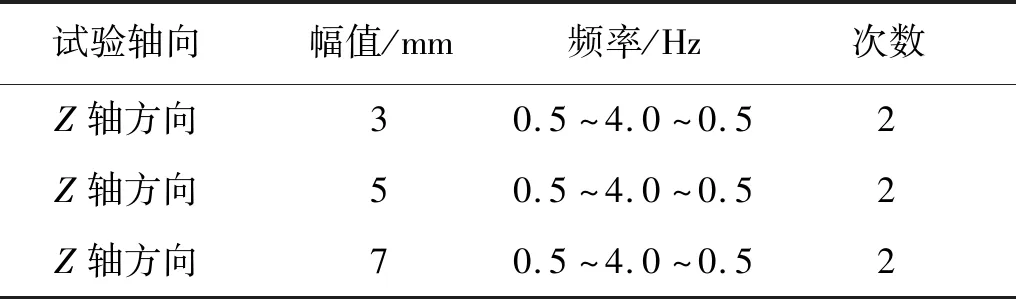
表2 正弦激励试验设置参数Tab.2 Parameters setting of sine excitation test
正弦激励试验可以连续测定系统在一系列设定频率下的响应。控制振动台从0.5 Hz开始振动,待系统运动状况趋于稳定时,采集质量块的位移信号数据。增加到下一设定的激励频率,重复上述操作。激励频率为间隔0.1 Hz测定一次系统响应幅值。将试验测得的响应时域波形的波峰和波谷差值的1/2作为系统响应幅值,响应幅值和激励振幅之比就是准零刚度隔振系统的位移传递率。
准零刚度隔振系统在不同小振幅简谐位移激励下的位移传递率试验结果、理论计算结果及数值仿真结果的幅频响应如图10(a)所示。

图10 位移传递率(3 mm,5 mm,7 mm)Fig.10 Displacement transfer rate (3 mm,5 mm,7 mm)
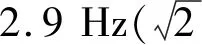
同时得到不同激励幅值下位移传递率最大值、最小值和均方根值并与理论结果进行比较,如表3所示。
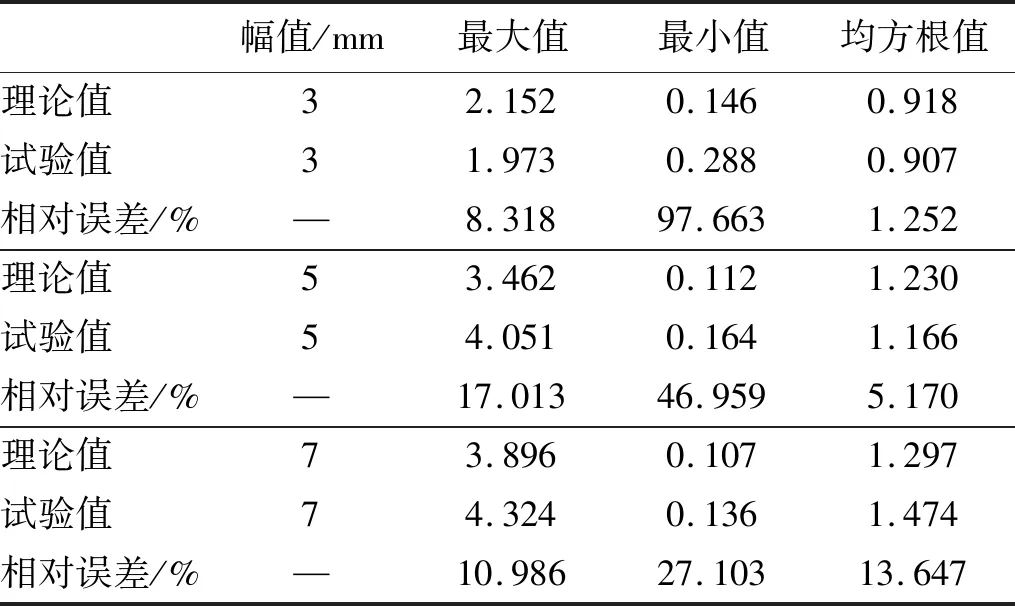
表3 试验结果与理论结果的数值比较Tab.3 Numerical comparison between test results and theoretical results
由表3可知,试验结果的最大值与理论值对比存在偏差,但在±20%的误差范围之内;最小值与理论结果的偏差较大,但随着激励振幅的增大误差率减小,这是由于小振幅激励时响应的最小值数值较小,对安装误差和试验参数变化更加敏感。均方根值与试验结果比较接近,偏差在14%以内,能够反映隔振系统的试验结果与理论结果的整体对比效果。综上分析,准零刚度隔振系统属于非线性系统,对试验参数的变化比较敏感,试验装置的加工精度及安装误差对试验结果造成一定的影响和偏差,但误差在合理范围内,从而验证了准零刚度隔振系统理论建模和分析方法的正确性。
6 随机振动工况仿真试验
6.1 TruckSim车辆与路面模型
车辆在实际工程中所受外界激励大都是随机的或者有很强的随机性[15],研究准零刚度隔振系统在随机振动工况下的响应更有工程应用价值。文献[16]结合动力吸振构型对电动车辆垂向性能进行研究,使系统的平顺性和操作稳定性得到了提升。由于六自由度振动试验台参数设置限制,不能进行随机振动工况试验。采用TruckSim/Simulink联合仿真,分析随机振动工况下系统隔振性能。
车辆模型为TruckSim中某8×8整车模型,如图11所示,文献[17]对该车辆模型进行了不同工况下的仿真试验,验证了该模型具有良好的操作稳定性和平顺性,满足此次仿真试验要求。

图11 8×8车辆TruckSim整车模型Fig.11 8×8 vehicle TruckSim model
路面模型采用文献[18]中基于分形理论建立的三维随机路面,该三维路面谱较高精度反映路面的三维纹理特性,既反映了路面纵向的不平顺激励,也满足仿真试验对随机路面横向高程变化的要求。选用B等级路面,并在TruckSim软件中编译,随机路面横断面设置及路面模型如图12所示。
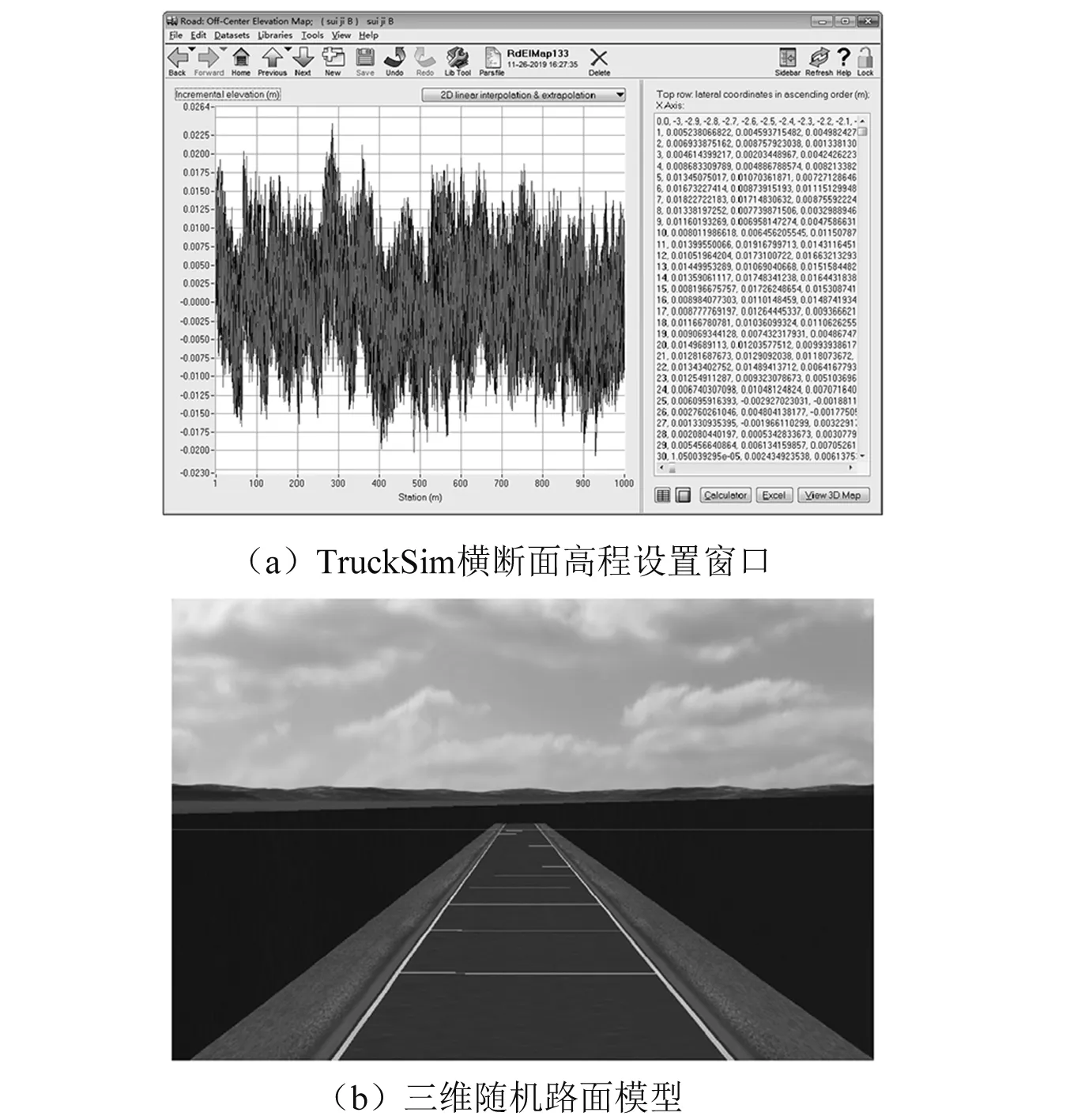
图12 TruckSim随机路面横断面设置及路面模型Fig.12 TruckSim cross section elevation settings window and three-dimensional random pavement model
6.2 TruckSim/Simulink联合仿真
由式(12)和上文确定的隔振系统相关参数,在Simulink中搭建其仿真模型。将TruckSim车辆模型中车体质心垂向位移响应、垂向速度、垂向加速度作为输出量,其中车体质心垂向位移响应作为Simulink模型的输入量,联合仿真模型如图13所示。
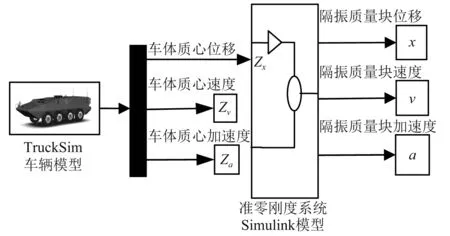
图13 TruckSim/Simulink联合仿真模型Fig.13 Co-simulation model of TruckSim/Simulink
隔振系统参数见表4,设车速为30 km/h,40 km/h,50 km/h,路面长度500 m,通过联合仿真,得到车体质心和准零刚度隔振系统的垂向位移响应、垂向加速度如图14所示。提取稳态数据得到位移响应、加速度均方根值及隔振效果,如表5所示。
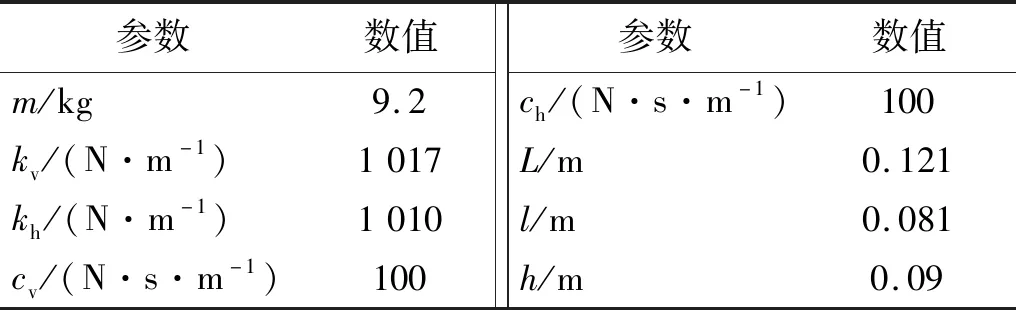
表4 隔振系统仿真模型参数Tab.4 Simulation model parameters of vibration isolation system
通过分析图14和表5,与车体质心处响应相比,隔振系统在车速30 km/h,40 km/h,50 km/h下垂向位移响应分别下降84.6%,82.4%,81.4%,垂向加速度分别下降90.1%,89.9%,89.7%,有效的降低外界激励对被隔振单元的影响。因此,所设计的QZS隔振器,在各车速下发挥了良好的隔振性能。
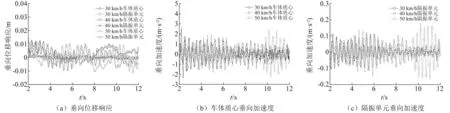
图14 车载随机激励工况仿真结果Fig.14 Simulation results of vehicle random excitation

表5 垂向加速度与位移响应均方根值Tab.5 RMS value of vertical acceleration and displacement response
7 结 论
通过正负刚度并联原理设计了一种结构简单、安装方便、占比空间小的准零刚度车载隔振系统,通过理论建模分析了系统参数对其隔振性能的影响,开展了简谐激励工况试验和车载随机振动工况仿真试验,主要结论如下:
(1) 静力学分析表明,隔振器系统刚度呈非线性,加工误差直接影响系统在静平衡位置的刚度,合理控制参数可使系统在静平衡位置的刚度趋近零。动力学分析表明,适当增大垂向阻尼或者减小激励幅值,可使系统共振峰值减小,且更好的实现低频隔振。
(2) QZS隔振系统的共振峰随着激励幅值的增大右移;准零刚度隔振系统的起始隔振频率更低,可有效降低系统的固有频率,表现出低频隔振性能;试验结果的最大值和均方根值与理论结果基本吻合,验证了准零刚度隔振系统理论建模和分析方法的正确性。
(3) 在随机路面激励下,车载准零刚度隔振系统的位移响应的均方根值同比车体质心降低80%以上,加速度的均方根值降低90%左右,可以在各车速下有效降低外界激励对被隔振单元的影响,具有良好的隔振效果。
