基于测后模拟原理的半波长输电线路暂态量纵联保护
2021-03-31韩一鸣束洪春达慧唐玉涛
韩一鸣, 束洪春, 达慧, 唐玉涛
(1.昆明理工大学 国土资源工程学院,昆明 650051;2.昆明理工大学 电力工程学院,昆明 650051)
0 引 言
半波长交流输电(half wavelength AC transmission,HWACT)是指输电线路的距离达到一个工频半波的超远距离的三相交流输电技术[1-4]。特高压半波长交流输电技术作为远距离、大容量的交流输电方式,其优势在于全线可以实现无功自平衡,不需要安装无功补偿设备。从功率传输的角度而言,其等效电气距离为0,理论上输电能力为无穷大[5-6]。从经济特性方面来说,相较于目前发展势头迅猛的特高压直流输电技术(UHVDC),半波长交流输电技术利用纯交流系统的自然特性,线路感性无功与容性无功相互抵消,首末两端电压相差180°,相当于变比为-1的变压器,因此无需直流输电系统复杂的运行控制模块,且输送容量更大[7]。随着我国电力需求的持续增长以及西部能源基地与东部负荷中心远距离大容量输电的客观要求使得特高压半波长交流输电技术可作为我国未来的输电方式之一。
半波长交流输电线路由于其输送距离远、电压等级高,正常运行状态以及故障状态下的电压电流分布特征都与传统交流输电线路不同,由于其分布参数特性显著,线路分布电容大,由于电容效应引起的过电压较严重,传统的交流线路保护方案不能直接用于半波长交流输电线路[8]。对于依靠工频测量阻抗的距离保护来说,半波长交流输电线路的测量阻抗随着故障点的位置不同呈现出非线性的变化趋势,线路在空间上的距离与其等效的阻抗不再呈现单调变化规律,无法有效区分出线路末端的正向出口故障与背侧的区外故障,存在严重的正向暂态超越问题[9]。对于纵联差动保护来说,半波长交流输电线路在发生故障后,难以准确计算电容电流并加以补偿,即此类保护方法对于半波长交流输电线路而言也不适用[10]。
文献[11]根据缩尺等效实验原理,在户外场地搭建了半波长缩尺实验线路,开展了半波长输电技术的实验研究。实测了不同末端负载下线路两端、中间、1/4和3/4处电压值,验证了稳态下半波长输电的点对点和过电压特性。文献[12]为了解决半波长线路过长所导致的动作量与故障点电流间的误差问题提出了一种基于贝瑞隆模型,能够保护线路全长的电流差动保护新方法,该方法通过在全线上人为设置3个参考点,来提高故障点电流计算值的精度,从而保证电流差动保护的灵敏性和可靠性。文献[13]利用半波长输电线路故障发生后线路两侧保护元件感受到故障的时间差来确定最优差动点,解决了长线路差动点与故障点不一致时,保护灵敏性会受到影响这一问题。在此基础上,文献[14]利用补偿电压和电流构造了基于全量和突变量的伴随阻抗,并通过该阻抗在区内外故障时的特征差异,来识别半波长线路的区内、外故障。文献[15]分析了方向纵联保护在半波长输电线路中的适用性,并指出了常规纵联保护应用于半波长输电线路时存在动作速度慢的问题。由于半波长线路反向故障时,波的折反射过程较长,文献[16]提出了一种适用于半波长输电线路的新型故障分量方向保护方法,该方法通过计算出反向识别系数,实现了对半波长线路反向故障时的快速识别。
本文分析了常规保护应用于半波长交流输电线路的不适应性,结合基于贝杰龙模型的半波长输电线路的运行特性,提出一种基于测后模拟原理的半波长输电线路暂态量纵联保护方法,将测后模拟原理与纵联保护相结合,利用发生短路故障后线路两端暂态电流计算至线路中点处实现半波长输电线路故障辨识,通过PSCADEMTDC验证了此保护方法的适用性,相比于工频量保护更加快速、可靠,并仿真证明了此方法具有较好的耐受过渡电阻能力且不受故障距离和故障角变化的影响。
1 常规保护适用性分析
半波长交流输电线路由于其超远的输电距离,相比于常规输电线路,故障信息发生了显著的变化。输电距离带来的最直接的影响是电磁波传播及通道延时增长,故障信息传送到两端线路的时刻存在显著差异。其次,沿线电压呈现非线性、不单调的波动特征。在理论分析上,对于半波长输电线路,基于集中参数的故障分析方法不适用,需要利用分布参数模型进行分析。
目前,距离保护、电流差动保护及方向元件等构成了超、特高压输电线路的保护配置方案。对于半波长输电线路,由于故障特征的空间特性,基于KVL的差动保护、基于阻抗线性特征的距离保护不再适用于半波长输电线路。
1.1 距离保护
当半波长线路沿线发生三相短路时,测量端电压、电流为:
(1)
由式(1)可知,半波长线路沿线不同位置发生三相短路故障时,保护安装处的测量阻抗为
Z=Zcth(γlF)。
(2)
半波长交流输电线路在沿线不同的位置上发生单相接地故障时,线路首端保护安装处的测量阻抗的幅值和相位分别如图1和图2所示,测量阻抗随故障点位置非线性变化,然而,距离保护是建立在测量阻抗与故障位置呈线性关系的基础上,对于半波长线路,无法区分线路首端及正向出口故障,存在严重的正向超越,故不适用于半波长输电线路。

图1 半波长线路沿线三相短路保护测量阻抗幅值Fig.1 Amplitude of measured impedance in a half-wavelength lines three-phase short circuit

图2 半波长线路沿线三相短路保护测量阻抗相角Fig.2 Phase angle of measured impedance in a half-wavelength three-phase short circuit
1.2 电流差动保护
在传统特高压线路中,由于电流差动保护原理简单、使用电气量单纯、保护范围明确、动作不需延时等优点得到了广泛应用。
半波长输电由于输电距离超长,受到分布电容电流的影响,需要对差动电流按下式进行电容电流补偿,补偿电流公式为
(3)
式中:Uφ为相电压;U0为零序电压;Xc0为正序容抗;Xc1为零序容抗。
由1.1节可知半波长输电线路故障后,沿线的电气量呈现出非线性、非单调的特征,无法准确计算出电容电流并对其进行补偿,现有的电流差动保护所依赖的差动电流无法得到,故常规的电流差动保护无法应用于半波长输电线路。
常规线路由于输电距离短,电磁波传输及通道延时对电流差动保护的速动性影响较小。相比之下,半波长输电线路超长的输电距离,传输延时最长可达30 ms,发生故障后,故障信息将在不同时刻传输到两侧保护。若故障发生在M侧近端,对于M侧保护,启动后30 ms内将产生虚假差流,需要闭锁差动保护,在此基础上,还需加上10 ms的保护计算时间,则自故障发生时刻到保护出口动作时刻,将有40 ms的延时,这是保护的速动性所不容许的。
1.3 方向元件
方向元件能够准确反映半波长输电线路末端发生正向出口故障时的母线背侧系统阻抗,也能反映反向故障时的半波长线路及对侧系统综合阻抗,半波长线路复杂故障特征不会影响方向元件的动作。若半波长输电线路利用方向元件构成纵连方向保护时,如1.2节分析所言,在故障发生于近端或者远端的情况下,保护启动40 ms后才能接收到对侧方向保护元件的动作信号,保护出口时间为感受到故障后40 ms,保护速动性较差。
由以上分析可知,传统的距离保护和电流差动保护无法直接应用于半波长输电线路,方向元件虽能准确反映故障方向,但由于电磁波传输及通道延时较长,保护时间显著大于现有线路保护动作时间,已不满足保护的速动性要求。
2 基于测后模拟的纵联保护原理
2.1 故障启动判据
半波长输电线路发生故障后,线路电压电流会发生变化,但是由于过长的输电距离导致线路两端保护安装处检测到的电气变化量不足以作为发生故障的判断依据。在此基础上,本文采用瞬时功率作为保护启动判据,满足速动性、灵敏性的要求。
定义瞬时功率为
P=uaia+ubib+ucic。
(4)
当线路正常运行时,由于传输功率是恒定的,测量端的瞬时功率应为恒值,如图3所示。
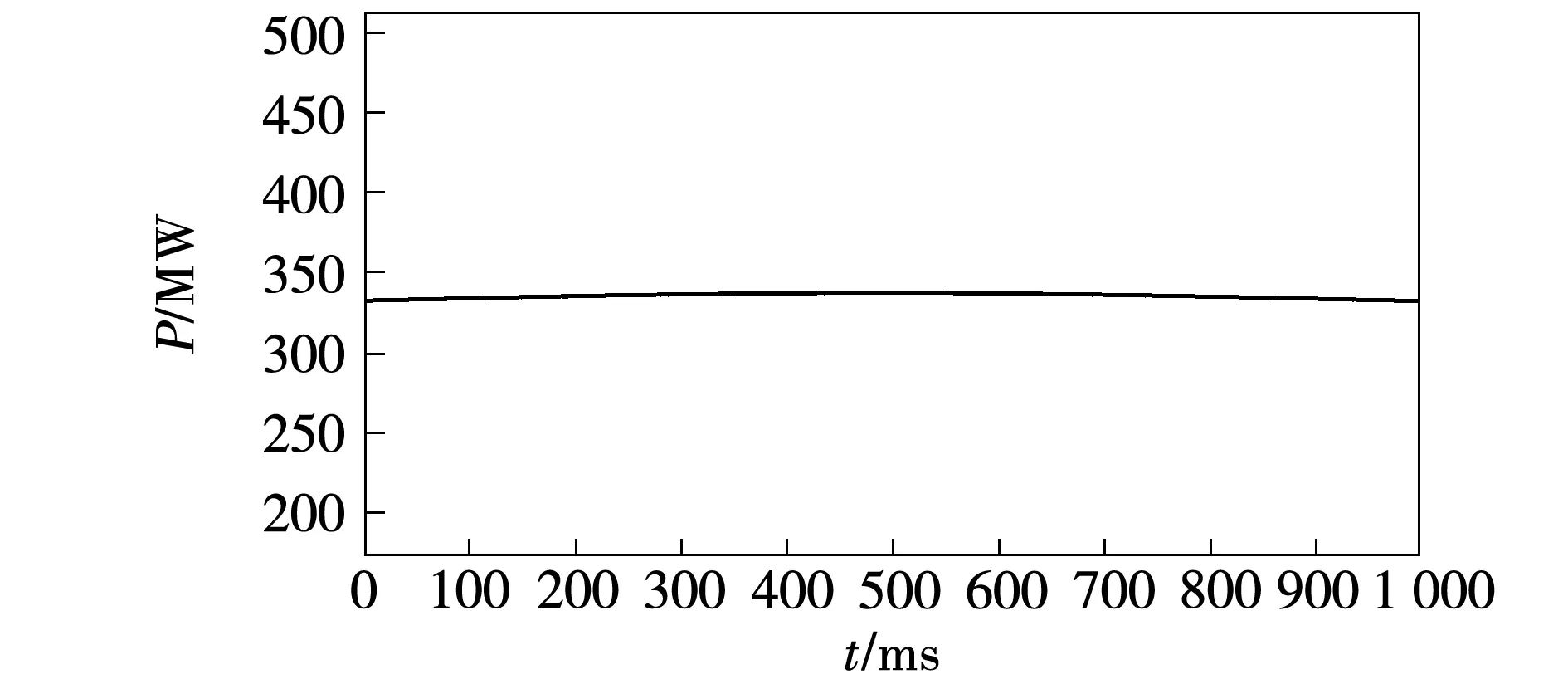
图3 正常运行时的瞬时功率Fig.3 Instantaneous power at normal operation
但发生故障时,故障相电流失去原本的正弦特性,故障点处电压也将随之变化,显然,瞬时功率相较于单一电流、电压信号变化将更加显著,故可作为保护启动判据,如图4所示。
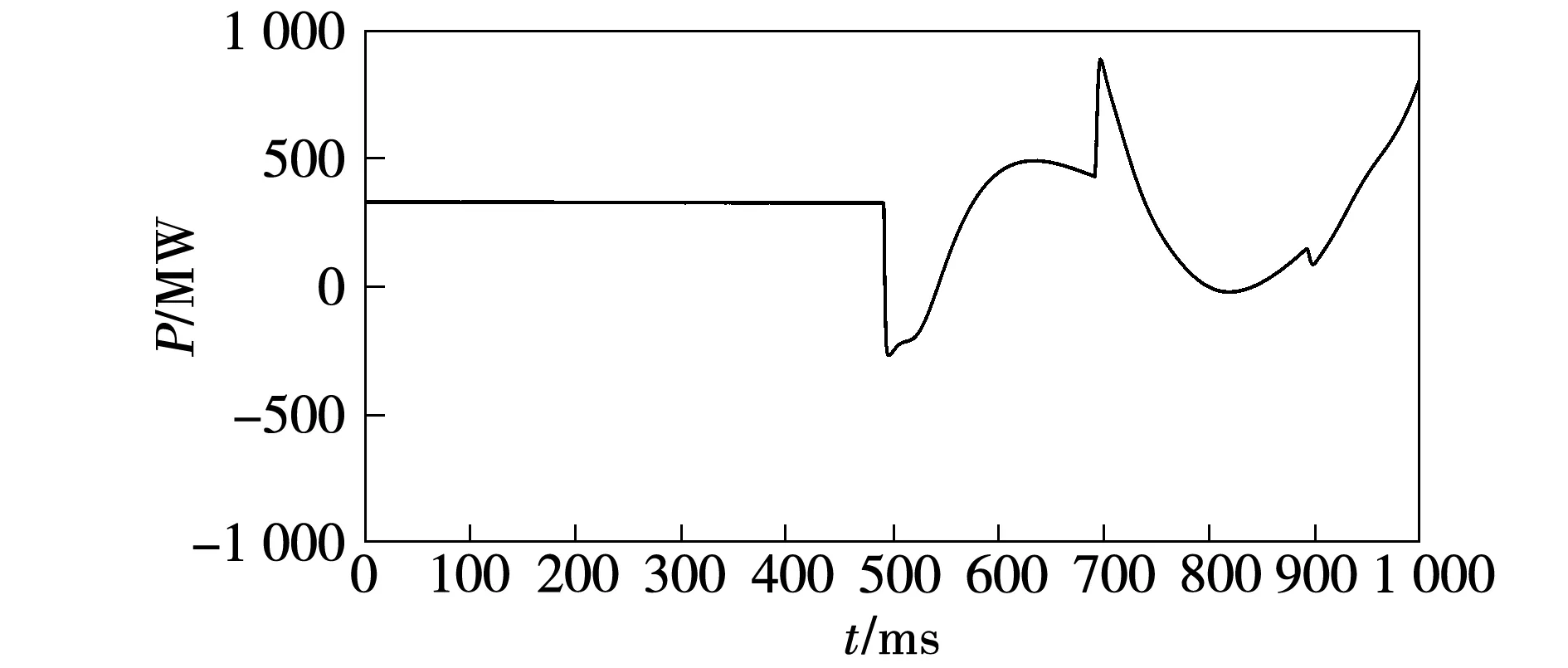
图4 发生故障时的瞬时功率Fig.4 Instantaneous power in case of failure
2.2 保护判据
上世纪90年代初,测后模拟原理被广泛应用于模拟电路故障诊断,先后提出了基于测后模拟原理的辐射状配网故障分支识别、中性点经消弧线圈接地的补偿电网单相接地选故障线、UHVDC线路(内部)故障辨识和电力变压器内、外部短路故障甄别方法。模拟电路故障诊断的测后模拟方法,其本质是在电路内部不含故障或者含有故障的假设条件下其电网络(模型)和参数的匹配和辨识之命题,因此,测后模拟原理可以作为电网络故障与健全两种模式的辨识之原理。输电线路电流纵联差动保护是利用被保护线路两端的电流,根据基尔霍夫电流定律、基于内部故障引起的不平衡电流实现的一种保护原理,选择性、灵敏性、速动性方面均具有优势。从故障信息的应用来看,它在提取并利用线路内部故障信息、反应线路故障方面具有很强的能力,这一点是其他保护无法比拟的。
假设被保护线路未发生故障,以输电线路等效模型为其基准模型,根据量测端的电压电流实测值按照线路模型的沿线电压电流分布规律,计算线路末端的电压电流,利用其模拟计算获取的线路末端电压电流与实测的电压电流进行比较、匹配,即可构成基于输电线路故障暂态电气量的纵联保护。当然,模拟计算所推求并进行比较匹配的点可以是线路末端,亦可以是其它方便描述和计算的点,比如线路中点。
如图5所示的仿真系统图中,假设被保护线路未发生故障,以输电线路(无故障)等效模型为基准模型,根据M端电压电流的实测值uM、iM按线路模型的电压电流分布规律计算输电线路中部的模拟电流iM,1/2,首先将M端测得的电流uM、iM做相模变换,计算线模分量,根据提取的母线M的保护安装处所获得的线模电流推算至线路中点得到中点电流iM,1/2。同理,可根据N端电压电流的实测值uN、iN按线路模型的电压电流分布规律计算输电线路中部的模拟电流iN,1/2,首先将N端测得的电流uN、iN做相模变换,计算线模分量,根据提取的母线M的保护安装处所获得的线模电流推算至线路中点得到中点电流iN,1/2。如图6所示。
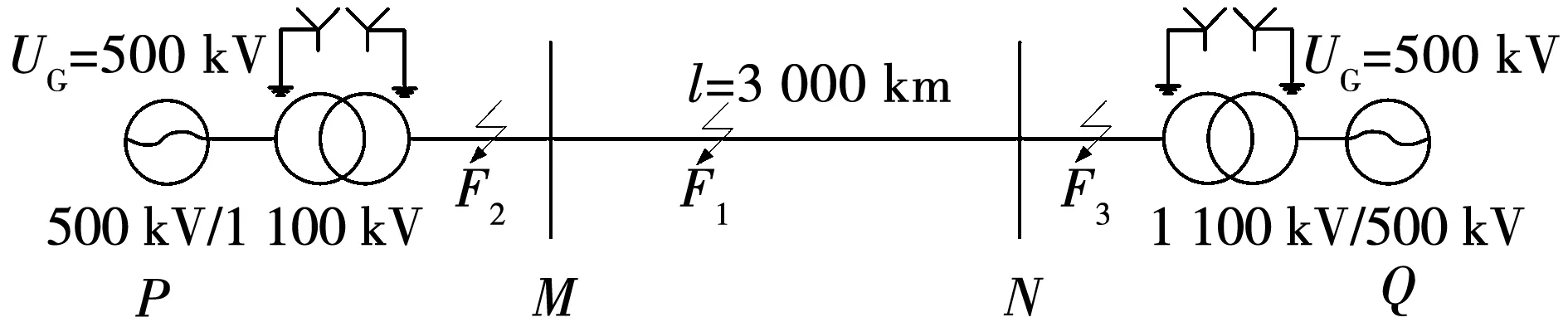
图5 仿真系统图Fig.5 Simulation system diagram

图6 两侧电压电流实测量计算线路中点的模拟电流Fig.6 Real measurement of voltage and current on both sides of the line to calculate the simulated current at the middle point of the line
将两侧测得的电压、电流做相模变换,计算线模分量并提取故障分量,根据提取的两侧母线M、N的保护安装处所获得的线模电流、电压故障分量推算至线路中点得到故障电流曲线,即
(5)
式中:iM,1/2、iN,1/2分别为从线路两端母线M、N推算至线路中点的电流;C为半波长输电线路全长的电容值;L为半波长输电线路全长的电感值;uM、uN分别为线路两端母线M、N测得的电压做相模变换后提取的故障分量值,iM、iN分别为线路两端母线M、N测得的电流做相模变换后提取的故障分量值。
相模变换公式(相电压变换为模电压、相电流变换为模电流)为:
(6)
(7)
式中:uα、uβ、u0分别表示α模、β模和零模电压;iα、iβ、i0分别表示α模、β模和零模电流;ua、ub、uc分别表示线路量测端测得的A、B和C三相电压;ia、ib、ic分别表示线路量测端测得的A、B和C三相电流。
将模拟电流iM,1/2与iN,1/2求和的绝对值于短时窗内积分,正方向均取从母线流向线路,在此定义δ为中点电流和的绝对值于短时窗内的积分,则δ的计算公式为
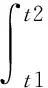
(8)
为了满足速动性的要求,式(8)中:t1=0、t2=2.5 ms;iM,1/2表示从母线M推算至线路中点的电流;iN,1/2表示从母线N推算至线路中点的电流。
若被保护线路未发生故障或线路MN发生外部故障时,线路MN本身电气参数未发生变化且没有附加故障源注入,M端和N端电压电流方向始终一致,且均满足贝杰龙线路模型关系,由线路两端电气量计算至线路中点2个模拟电流大小相同,方向相反,电流和绝对值的短时窗积分δ近似为0。若被保护线路MN发生故障时,线路MN电气参数改变,且内部出现附加故障激励源,不再满足原有的贝杰龙模型关系,M、N两端电压电流经贝杰龙模型推算至线路中点时将不再相等,即计算得到的δ不为0。据此可分别提出基于测后模拟算法的电流纵联保护判据:
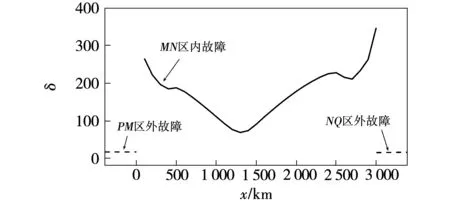
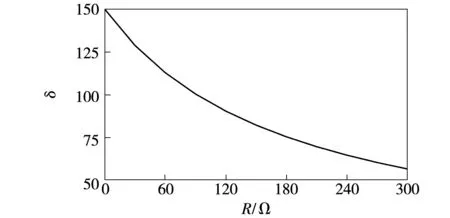
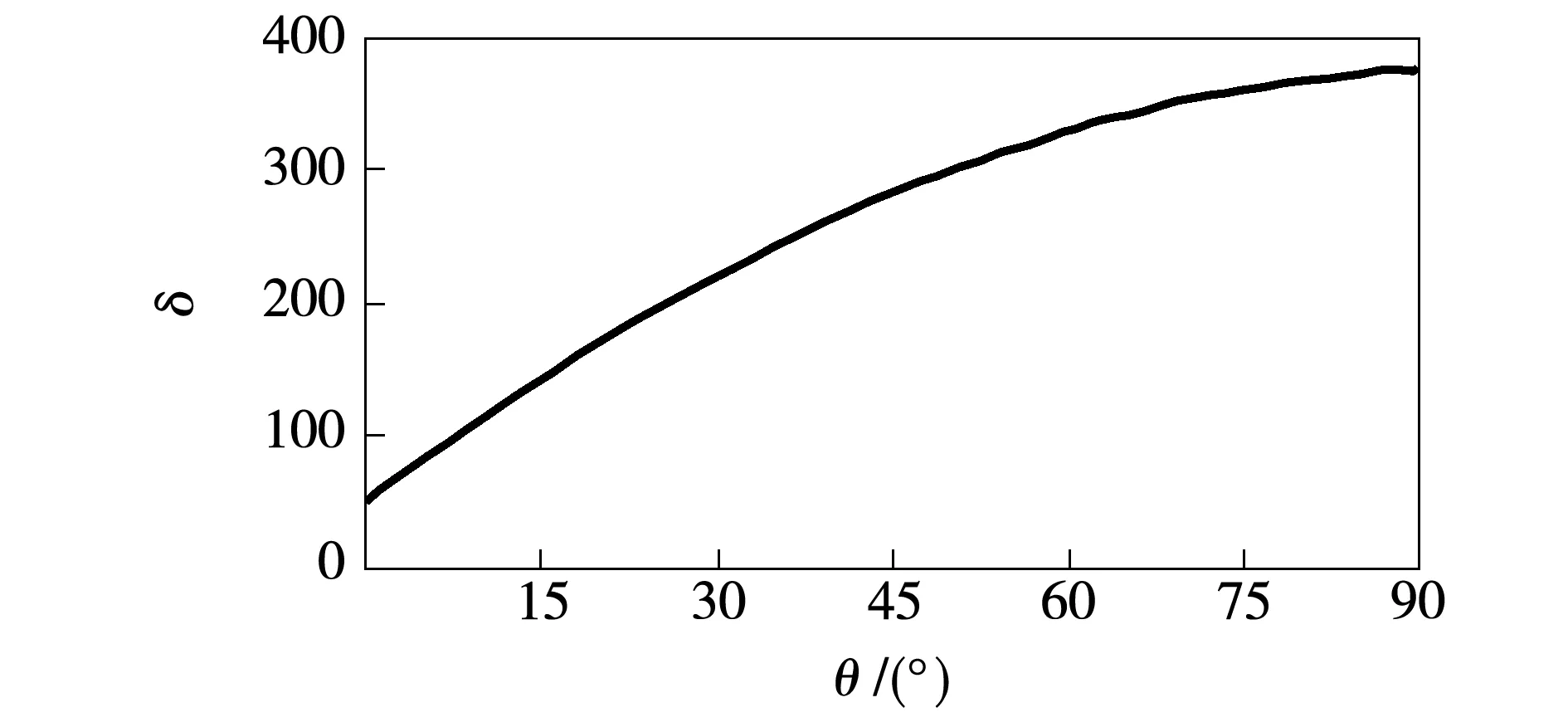
若δ (9) 则被保护线路区内未发生故障; 若δ≥kδset, (10) 则被保护线路区内发生故障。 式中:δset为被保护线路无故障情况下,M、N两侧所推得的线路中点处模拟电流之和的最大值;k为可靠系数,考虑到两侧线路保护CT存在误差,区外故障时计算中点处短时窗电流积分不一定为0,因此需要设置可靠系数k以保证区内外故障的准确、可靠辨识,经过大量仿真遍历数据验证,将δset取30,可靠系数k取1.5效果最好。 本文的仿真采用PSCADEMTDC搭建半波长输电线路仿真模型,模型如图5所示。模型参数选用特高压1 000 kV线路参数[17],以图7所示特高压杆塔作为特高压半波长输电线路杆塔,设线路均匀换位,两端电源系统,根据计算线路全长2 938 km,仿真采样率设置为10 kHz。利用图5所示仿真系统对线路MN内距M侧1 300 km处F1点、母线M的反方向F2点以及母线N反方向F3点3处故障情况分别进行分析,M侧以及N侧推算至中点的电流如图6所示,三相线路经过相模变换解耦后,忽略长线路的电阻和电导,计算得到工频且α模波阻抗Zc=246.11 Ω、光速v=2.98×108m/s时窗长度为2.5 ms。图8(a)、(b)、(c)分别为线路MN、母线M侧反方向PM和母线N侧反方向NQ上故障时,由M、N两侧电气量分别计算得到的线路中点处α模电流模拟波形iM,1/2与iN,1/2。 图7 线路杆塔模型Fig.7 Tower model 图8 区内、外单相接地故障时线路中点处模拟电流Fig.8 Analog current at the midpoint of the line when single-phase ground fault occurs internal and external 由图8(a)可以看出,线路MN区内故障时,双端电气量推至线路中点处模拟电流波形极性相同,此时根据式(8)计算得到的δ=80。对于区外故障,由图8(b)、(c)可以看出,M端和N端电气量推算至线路中点所得模拟电流波形iM,1/2与iN,1/2波形极性相反,此时应用式(8)可计算2.5 ms时窗内的δ=10。与图8(b)、(c)相比,图8(a)区内故障时电流和的值很大,以此差异可构成判别被保护线路故障与否的判据。 基于测后模拟原理的纵联保护其原理本质是线路区内故障改变了线路本身电气参数,线路中间出现了附加故障激励源,两端的电气量参数不再满足原有贝杰龙模型关系,与故障类型不存在直接关系,因此本方法不仅适用于单相接地故障,对于两相短路故障和两相短路接地故障同样适用。以3.1节仿真模型为基础,在线路MN上距离M端600 km的F1处、PM段F2处以及NQ段F3处分别设置AB两相短路故障以及AB两相短路接地故障,故障设置为金属性短路。两相短路故障、两相短路接地故障后两端电流计算至线路中点的模拟电流波形分别如图9、图10所示。 MN线路区内故障时根据式(8)计算线路中点计算电流短时窗积分和分别为δ=100(两相短路)与δ=112(两相短路接地)。区外故障时由图9、图10(b)、(c)可以看出,中点计算电流呈现方向相反,幅值相近的特性,这将导致线路中点计算电流绝对值远小于线路MN区内故障时的中点计算电流绝对值,根据实际计算,4种情况下线路中点电流和在短时窗内的积分和δ最大值为25,可见对于两相短路与两相短路接地故障,基于测后模拟原理的纵联保护依旧能够准确实现线路故障区段的辨识。 图9 区内、外两相短路故障时线路中点处模拟电流Fig.9 Analog current at the midpoint of the line when two-phase short fault occurs internal and external 图10 区内、外两相短路接地故障时线路中点处模拟电流Fig.10 Analog current at the midpoint of the line when two-phase ground fault occurs internal and external 对于故障危害最严重的三相短路来说,其本身故障分量相较于3.1节的单相接地故障与3.2节的两相短路与两相短路接地故障更大,附加激励源能量更高,因此对于测后模拟原理适应性更好。根据3.1节仿真模型设置线路MN上距离M端600 km的F1处、PM段F2处以及NQ段F3处三相短路故障,线路中点计算模拟电流波形如图11所示。 由图11可以看出而对于被保护线路MN区内故障,由M、N两侧电气量计算得到的线路中点处电流iM,1/2与iN,1/2波形差异性较大,这是由于三相接地故障较强,短路电流大,故障分量也更大,使得原有的线路运行状态发生较大改变,从而导致基于无故障线路双端电压电流量推导得到的中点电流值与实际不符,此时计算出的δ值为360,为所有故障类型中计算电流短时窗之和最大的情况,而区外故障计算出的δ值为36,也相对较大,由此可见若没有可靠系数k,半波长输电线路发生三相故障时,将出现保护误动作的情况。 图11 区内、外三相短路故障时线路中点处模拟电流Fig.11 Analog current at the midpoint of the line when three-phase short fault occurs internal and external 3.4.1 故障距离的影响 对于半波长输电线路这种超长线路输电体统,故障距离的不同很大程度上将影响保护动作的可靠性,本文以3.1节中的3 000 km输电线路模型为基础,考虑不同故障距离对判据可靠性的影响,以100 km的增量对线路MN区内外全长进行遍历,以单相接地故障为例,故障初始角70°,故障过渡电阻设置为10 Ω,根据式(8)计算线路中点处的模拟电流之和的绝对值短时窗内积分δ随故障距离变化如图12所示。可以看到,被保护线路MN区内故障时,δ始终大于50,而区外故障时,δ几乎为0。由此可见,故障位置对于电流和的短时窗积分构成测后模拟纵联保护判据影响很小,判据对线路全长均有可靠性。 图12 中点处电流计算积分随故障距离的变化规律Fig.12 Variation of midpoint current and fault distance in transmission line 3.4.2 故障过渡电阻的影响 对于依靠电气暂态量的测后模拟纵联保护来说,过渡电阻的大小将改变暂态过程的强弱,直接影响到保护判据的可靠性,本节以3.1节中半波长输电线路模型为基础,考虑故障时过渡电阻的影响,假设在线路MN内距M端600 km处发生A相接地故障,保持故障角为70°不变,过渡电阻从0以30 Ω递增至300 Ω进行仿真,δ随故障点过渡电阻的变化如图13所示。 图13 中点处电流计算积分随过渡电阻的变化规律Fig.13 Variation of midpoint current and transition resistance in transmission line 由图13可见,随着故障过渡电阻的增大,根据式(8)计算线路中点处的模拟电流之和的绝对值短时窗内积分δ逐渐减小,高阻故障时,δ仍可以超过50,因此,基于测后模拟原理的纵联保护具有较好的抗过渡电阻能力。 3.4.3 故障初始相角的影响 故障发生时刻故障角对于以暂态量为基础的测后模拟纵联保护有一定影响,故障角不同,其故障后的暂态过程强弱也有不同,本节依旧以3.1节仿真模型为例,考虑故障初始角的影响,假设在被保护线路距母线M端600 km处发生单相接地故障,过渡电阻设置为10 Ω,故障初始角从0开始,以5°为间隔递增长至90°进行遍历,线路中点处的模拟电流之和的绝对值短时窗内积分δ根据式(8)计算,δ随故障初始角的变化分别如图14所示。 图14 中点处电流计算积分随故障初始角的变化规律Fig.14 Variation of midpoint current and initial fault angle in transmission line 由图14可知,δ随故障初始角增大而增大,即使在初始角为0时,其中点模拟电流之和视窗内积分δ可达到50,较区外故障时仍较大,由此可知在小角度故障的情况下利用模拟电流和构建的判据仍然可靠。 由以上分析可知,基于贝杰龙模型的测后模拟暂态量纵联保护能够可靠判断被保护线路是否故障,且几乎不受故障距离、过渡电阻的影响,受故障初始角的影响较小。经大量全线范围内仿真分析验证,δset取为30,可靠系数k均取为1.5,可以满足保护可靠性要求,不会出现误动。 本文分析了半波长交流输电线路区内外故障时线路两侧暂态电流特性,根据贝杰龙线路模型将两侧电流推导至线路中点计算两侧电流之和绝对值在短时窗的积分,以此为构造区内外辨识判据,通过分析得出以下结论: 1)线路区内故障时,由于线路本身电气参数发生改变,两端电气量不再满足原本贝杰龙方程,因此两侧电流推导至线路中点时初始极性相同,线路中点计算电流之和的绝对值较大,其在短时窗内积分将与保护区外故障或者未故障情况产生较大差异,依靠此原理形成的基于测后模拟原理的暂态量纵联保护可以可靠识别故障区段。 2)测后模拟原理的暂态量纵联保护基于暂态电气量,依靠短时窗内的中点计算电流计算积分值,保护原理简单,计算速度快,满足半波长交流输电线路保护的速动性要求。 3)基于测后模拟原理的暂态量纵联保护其本质是被保护线路电气参数的改变导致两端电气量计算至线路中点时产生不同,与被保护线路发生何种电气改变无关,因此具有良好的抗过渡电阻特性,且不受故障距离和故障角影响。3 保护方法仿真分析
3.1 单相接地故障仿真

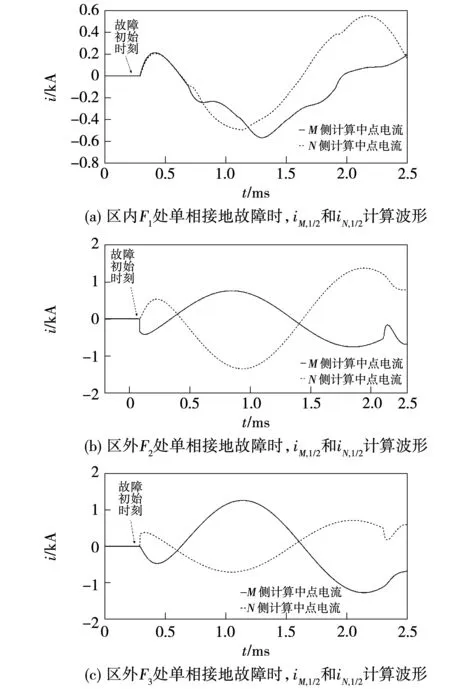
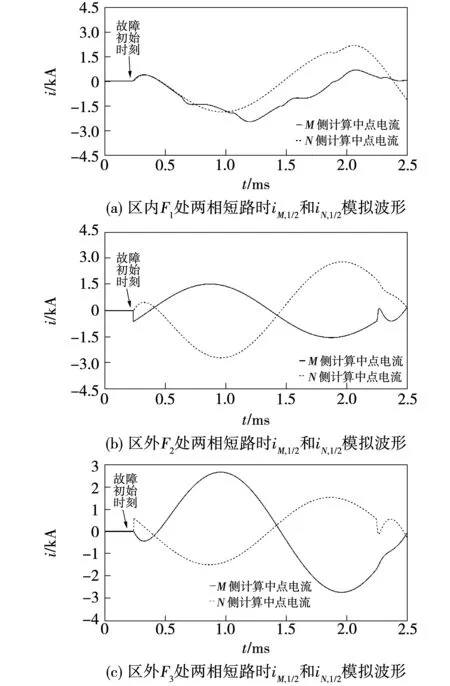
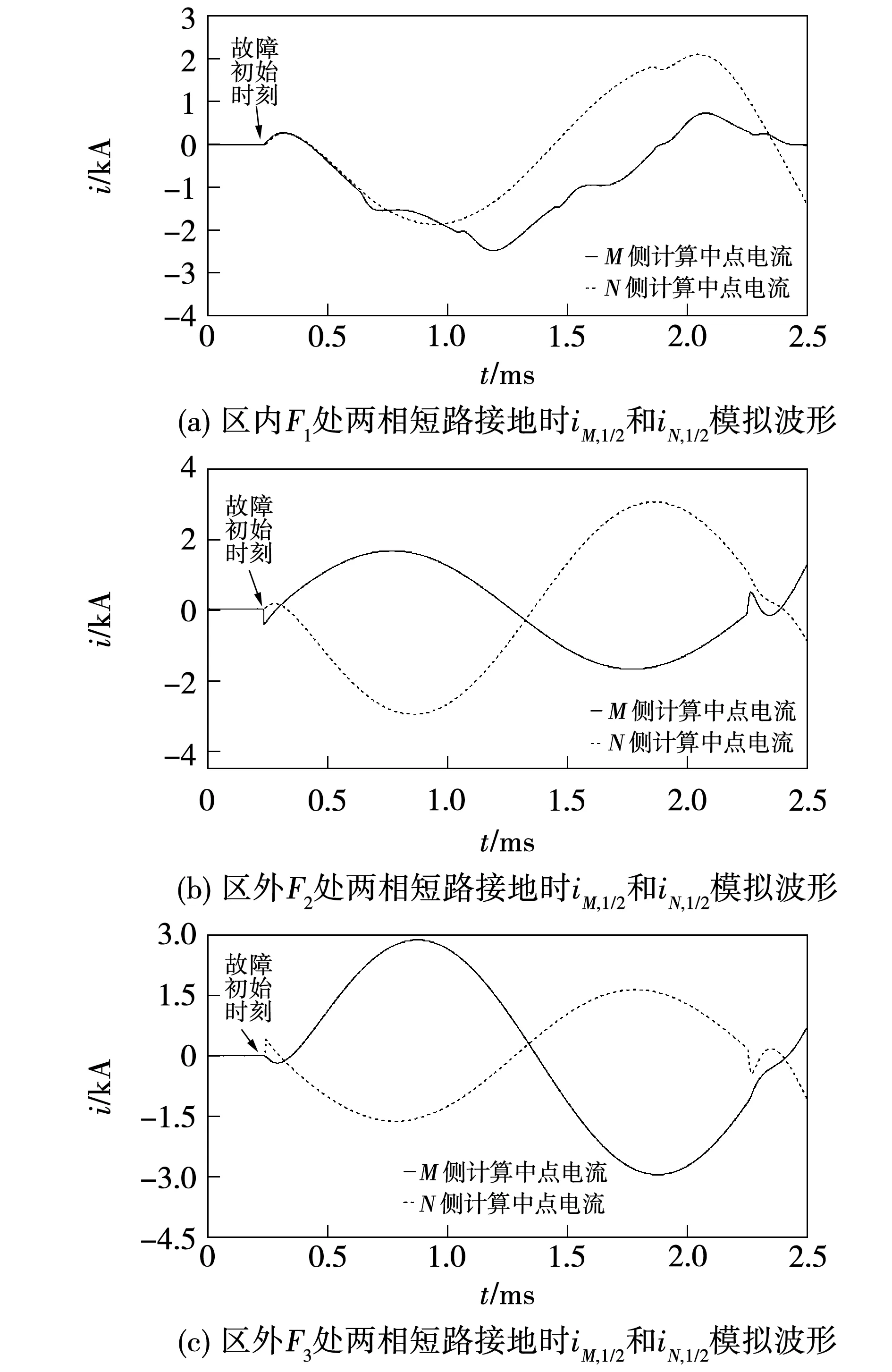
3.2 两相短路和两相短路接地故障仿真
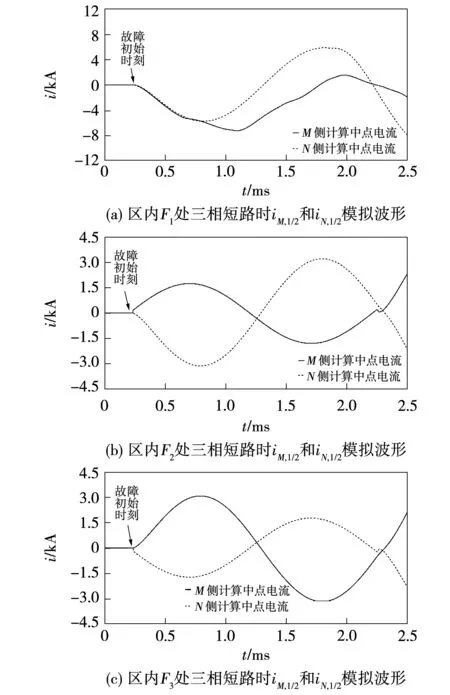
3.3 三相短路故障仿真
3.4 故障距离、过渡电阻以及初始相角的影响
4 结 论
