基于改进暂态能量方向的半波长输电线路保护方法

束洪春， 韩一鸣1，， 达慧， 曹璞璘， 范作云， 唐玉涛

(1.昆明理工大学 国土资源工程学院，昆明 650051；2.昆明理工大学 电力工程学院，昆明 650051)

0 引 言

半波长交流输电技术是指在工频运行条件下，传输距离为半个工频波长的超远距离交流输电技术，于20世纪40年代由苏联学者首次提出[1-3]。近些年来，随着±1 100 kV特高压直流输电(UHVDC)工程的成功投运以及模块化多电平换流技术(MMC-HVDC)的成熟，长距离、大容量的输电方式逐步成为了目前最合理的能源传输的手段[4-7]。半波长交流传输技术作为一种长距离、大容量的交流输电方式具有全线无功功率自平衡的优点，不需要沿线安装相关补偿设备[8]。在经济特性方面，与特高压直流输电技术相比，半波交流输电技术利用了纯交流系统的自然特性，无需额外运行控制设备，在3 000 km输电距离下输送相同功率输电成本仅为 UHVDC的一半[9]。现如今，半波长输电领域内相关的基础课题研究已经被纳入中国国家电网公司的战略发展规划，并且受到国内外学者的广泛关注[10-14]。

长距离与大规模分布电容导致半波长输电线路故障时线路沿线电压及电流的分布特征与传统交流线路完全不同，故传统保护原理在半波长输电线路中适应性需要具体分析。对于传统保护方法来说，半波长交流输电线路的测量阻抗随着故障点的位置不同呈现出非线性的变化趋势，线路在空间上的距离与其等效的阻抗不再趋于线性化的关系，且故障后相关电气量在沿线上呈现出非线性、非单调的特征，难以准确计算电容电流并加以补偿，故而传统距离保护以及纵联差动保护对于半波长线路不再适用[15-16]。

文献[17]提出了一种利用线路伴随阻抗保护的方法来进行半波长交流输电线路的适应性研究，此方法需要同时利用到输电线路两端的全信息电气量，因此需依赖电磁通道。文献[18]发现故障行波量、稳态工频量和故障突变量依然能够来表示半波长输电线路在发生故障后准确的故障方向，为方向元件应用于半波长交流输电线路的保护奠定了基础。文献[19]推导出了半波长交流输电线路无功功率损耗的分布规律，并求解出了沿线上的最高电压及其对应位置。文献[20]分析了半波长交流输电线路上行波的传播特性，在考虑了半波长输电线路依频特性的前提下，对线模和零模行波在线路发生故障后所体现出波速上的不同进行分析。文献[21]介绍了一种适用于半波长输电线路的Bergeron差动的改进保护算法, 该算法从原理上解决了传统的Bergeron差动保护应用在半波长交流输电线路上时由于计算值受到参考点影响而存在的问题。

本文针对半波长输电线路的特点提出了一种暂态能量方向的半波长输电线路保护方法。将初始行波、暂态行波和工频稳态归纳为统一行波的概念，在此基础上提出统一行波的故障分析法，兼顾了保护可靠性和速动性两方面的要求。由于暂态能量方向元件的能量和功率信息始终是存在于故障的初始瞬间、暂态和稳态期间，因此故障过程可视为行波能量和功率在新的边界条件下通过行波的多次折反射不断地重新达到平衡的一个过程，在这一基础上提出的暂态能量方向纵联保护将可快速、有效识别线路区内故障，实现线路保护。

1 半波长输电线路故障特征分析

1.1 半波长线路接地故障时测量阻抗特征

半波长线路沿线不同位置发生接地故障时，保护安装处的测量阻抗[22]为

Z=Zce(γxF)。

(1)

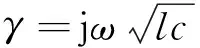
半波长输电线路在沿线不同的位置上发生接地故障时，首端的测量阻抗的幅值和相位分别如图1和图2所示。测量阻抗随接地点的位置不再呈现单一线性变化，线路测量阻抗的幅值关于线路的中点对称，其最大值出现在距离线路首端1 500 km处，在线路首端和末端发生故障时，测量阻抗的幅值是相等的，因而不能够区分出故障在线路首端还是正向末端出口处，继而容易产生暂态超越问题，传统的距离保护便不再适用。

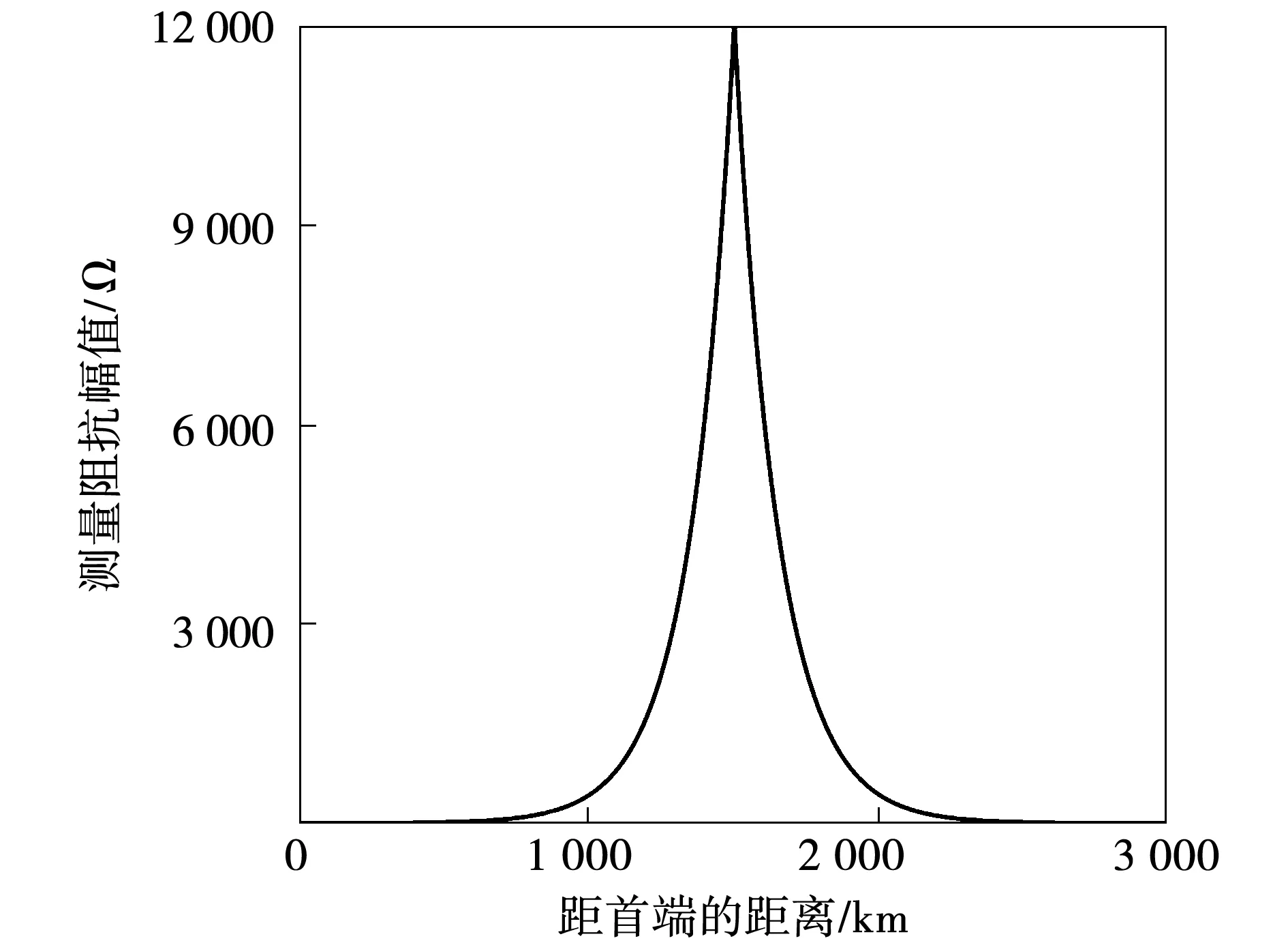
图1 半波长线路沿线三相短路保护测量阻抗幅值Fig.1 Amplitude of measured impedance in a half-wavelength line three-phase short circuit

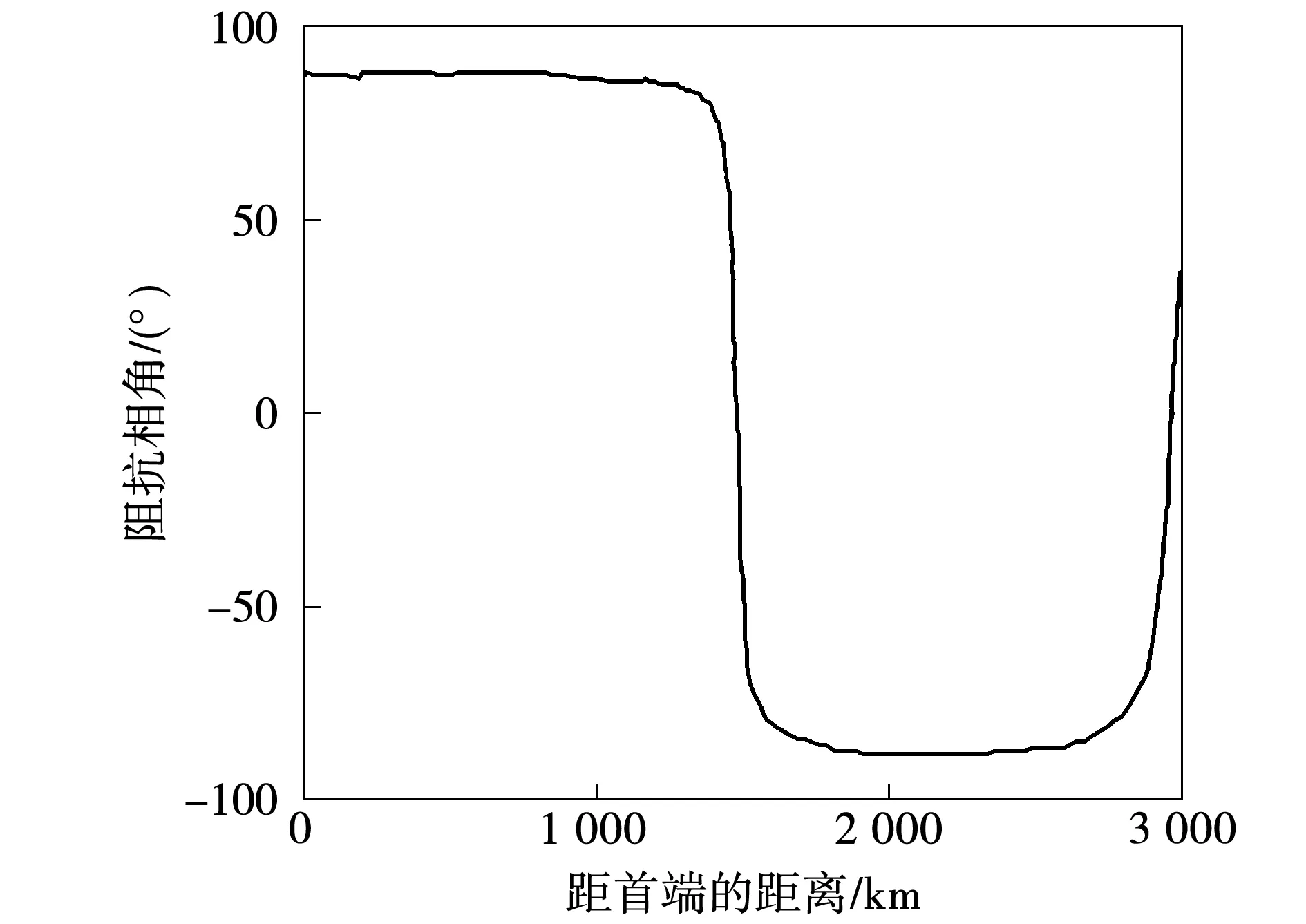
图2 半波长线路沿线三相短路保护测量阻抗相角Fig.2 Phase angle of measured impedance in a half-wavelength three-phase short circuit

1.2 半波长输电线路行波特性分析

特高压半波长线路由于超长的传输距离使得其在继电保护方案设计时需考虑线路参数的频变特性，行波在沿着线路传播的过程中会发生一定的畸变和衰减，行波的初始波头随着传播距离的增加会变得越来越平缓，相较于普通线路而言，行波在超长的交流输电线路上传播将导致更加严重的波形上的衰减和畸变。传输常数反映出了一定能量的衰耗和相位的移动，由于输电线路上电阻的存在而产生能量的衰耗，电能按照电磁波的形态在输电线路上传送的本质便有了相位移动，其计算公式[22]为

(2)

式中：实部α称为衰减常数；虚部β称为相位常数。由于线路参数R0、L0、C0、G0均为已知参数，化简可得

(3)

根据式(3)可计算衰减常数α，α表示入射波和反射波沿线的衰减特性，其单位通常用Np/m。在半波长输电线路运行条件下，可通过计算得到不同频率、不同位置产生的行波到达测量端的衰减程度，具体计算结果如图3。

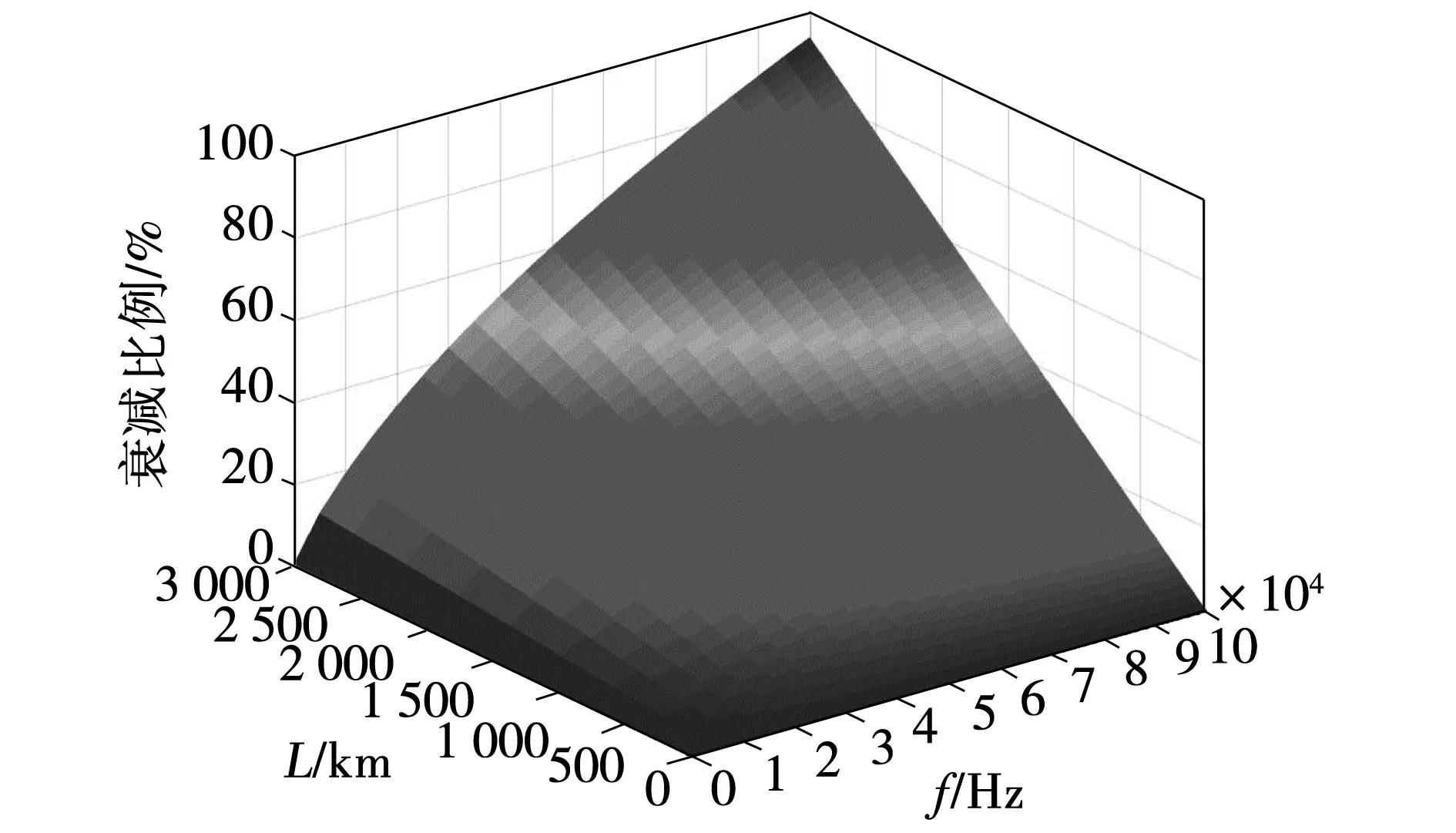
图3 不同频率、位置下行波衰减情况Fig.3 Attenuation of traveling waves at different frequencies

由图3可见，行波在半波长输电线路中传播衰减很快，超过一定距离发生的故障将很难在保护安装处检测到故障行波初始波头，因此很难以行波波头检测作为半波长输电线路的继电保护启动判据。

1.3 故障后工频波形特征及工频变化量保护适用性分析

常规工频变化量的保护是以工频的故障分量为基础，事实上，基于工频的故障分量以及序分量的功率方向判别元件利用线路背侧的测量阻抗特征能够实现对输电线路上正向与反向故障的判别，但过长的输电线路使得保护安装处感受到的故障工频分量的变化并不明显，故障前后故障相电压电流变化如图4所示，由图4可以看出故障发生后保护安装处检测到故障相的△u、△i很小，加大了工频变化量保护的难度，同时过长的通道延时导致保护动作时间明显大于现有特高压半波长交流输电线路保护的动作时间。而且，半波长交流输电线路发生反方向故障时，因半波长交流输电线路的波过程来回的折反射时间相对较长，常规保护的方向元件不能够在保护启动后快速而准确地判别反向故障。

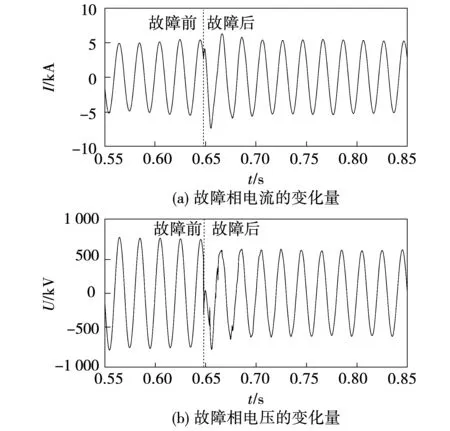
图4 工频变化量示意图Fig.4 Power frequency variation diagram

1.4 纵联差动保护适用性分析

半波长输电线路故障后，沿线的电压、电流等电气量呈现非线性分布，加之过长的输电距离导致分布电流不可忽视，传统高压交流输电线路中依靠两端作为差动点的纵联差动保护适用性受限。

与此同时，电流差动保护还受到通道传输延时的影响，常规线路电磁波传播及通道延时较短，对保护速动性影响较小。但由于半波长输电线路超长的输电距离，电磁波传播及通道延时最长可达30 ms。发生故障后，两侧保护将在不同时刻感受到故障。若故障发生在M侧，对于M侧保护，启动后30 ms内将产生虚假差流，需要闭锁差动保护，在此基础上，保护整定时间还需增加，则自故障发生时刻到保护出口动作时刻，将有超过30 ms的延时，这是保护的速动性所不容许的。

2 暂态能量方向保护原理

2.1 故障启动判据

输电线路发生故障后，线路电压电流会发生变化，但是变化量不足以作为发生故障的判断依据。在此基础上，本文采用瞬时功率作为保护启动判据，满足速动性、灵敏性的要求。

定义瞬时功率为

P=uaia+ubib+ucic。

(4)

当线路正常运行时，由于传输功率是恒定的，测量端的瞬时功率应为恒值，如图5所示。

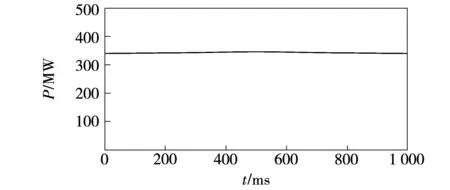
图5 正常运行时的瞬时功率Fig.5 Instantaneous power at normal operation

但发生故障时，故障相电流失去正弦特性，故障点处电压也将随之变化，显然，瞬时功率变化将更加显著，故可作为保护启动判据，如图6所示。

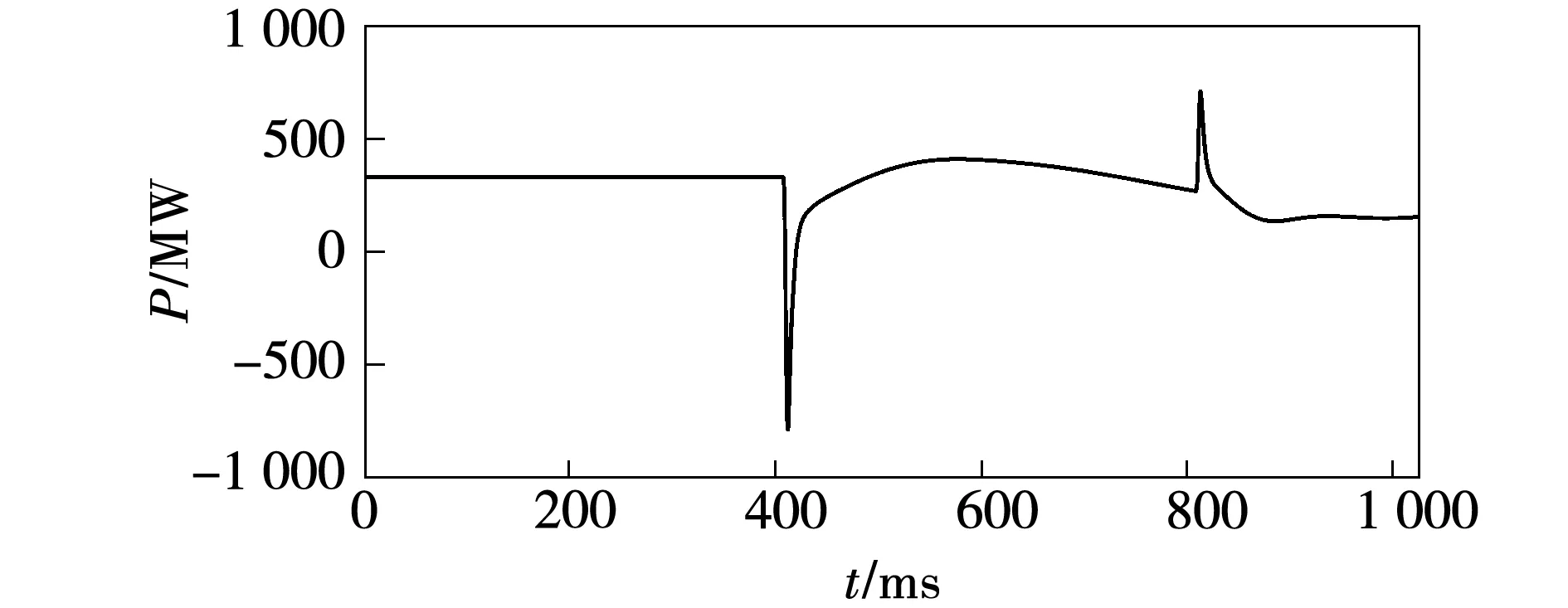
图6 发生故障时的瞬时功率Fig.6 Instantaneous power in case of failure

2.2 保护判据

在特高压交流输电系统中，两相运行状态下将产生较高的过电压，在线路中点处可达到1.7 pu，不允许采用单相重合闸，只能三跳三合[23]，因此，保护测量元件采用分相采集，不需要进行故障选相。本文所提出的保护原理是以相量为基础，不涉及模量，因此，在保护启动算法中不需要进行相模变换。暂态能量方向保护原理利用了故障附加激励产生的电流行波、电压行波含有的故障信息，可以在极短的时间内检测出故障，具有动作速度快的优点，但由于暂态行波信号的不确定性和不可重复性限制了行波保护的可靠性。因此，本文将初始行波、暂态行波和工频稳态可统一为行波的概念即统一行波，在此基础上提出的统一行波的故障分析法，兼顾保护速动性与可靠性的要求。由于暂态能量方向元件的功率和能量信息恒存在于故障初瞬、故障暂态和故障稳态期间，故障过程因而可视为行波功率和能量在新的边界条件下通过行波的反复折反射重新达到平衡的过程。

当输电线路发生区内故障时，按照叠加原理可以分解为正常负荷状态和故障分量附加状态，其故障分量状态如图7(a)所示；同理，当区外故障时，根据叠加原理，分解出其故障分量附加状态，如图7(b)所示。在图7中，可看出其电压、电流以及功率的方向，根据正、反向故障时的附加状态图，进而分析得出线路区内外故障的判据。

图7 正、反方向故障附加状态Fig.7 Additional states of positive and negative direction faults

图7中P、Q分别线路两侧等效系统，M、N为对应两侧系统的母线，Δu、Δi为线路电压和电流故障分量(图中箭头方向仅代表参考方向，不代表实际方向)，图7中故障分量系统是一个单激励网络，故障前系统各元件的初始值都等于0，为无源网络，故障发生时(t时刻)相当于在故障点F处附加上一个与当前时刻相电压大小相等方向相反故障等效电源UF(t)。Δu、Δi相乘即可得到瞬时功率，其符号代表了功率方向，功率在一定时间段Δt内积分即可得到能量，称为暂态能量。令

P(t)=ΔuaΔia+ΔubΔib+ΔucΔic；

(5)

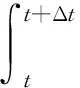
(6)

式中：t表示故障发生时刻；E(t)为线路母线两侧系统之间交换和传递的能量，即暂态能量，系统中暂态能量是由短路时附加故障激励UF(t)注入到系统的。规定电流正方向为母线指向线路的方向，当M侧正方向故障时：

(7)

EM(t)、EN(t)分别为M侧方向继电器K1与M侧方向继电器K2检测到的暂态能量，EFM(t)、EFN(t)为附加故障激励UF(t)产生能量分别经输电线路到达母线M、N处的能量，由于能量从故障点产生且系统中同时存在的电感和电容时刻发生着能量的交换，EFM(t)、EFN(t)在故障后的任一时刻都将储存一定的能量，即EFM(t)、EFN(t)始终大于0。故有：

(8)

当线路M侧反方向故障时：

(9)

其中EFM(t)、EFN(t)分别由附加故障激励UF(t)产生且同时为正，此时有：

(10)

据此，根据母线M、N两侧的方向继电器K1、K2检测到的暂态能量方向，提出保护判据：

(11)

具体保护逻辑如图8所示。

图8 保护动作逻辑框图Fig.8 Protection action logic diagram

3 暂态能量方向保护仿真分析

3.1 单相接地故障仿真分析

本文的仿真采用PSCADEMTDC搭建半波长输电线路仿真模型，模型如图9(a)所示。模型参数选用特高压1 000 kV交流线路参数，以图9(b)所示特高压杆塔作为特高压半波长输电线路杆塔[24]，设线路均匀换位，两端电源系统，线路全长3 000 km，仿真采样率设置为10 kHz。利用图9(a)所示仿真系统对线路MN区间内F1点和母线M的反方向F2点两处故障情况进行分析，M侧瞬时功率与暂态能量曲线如图10所示。

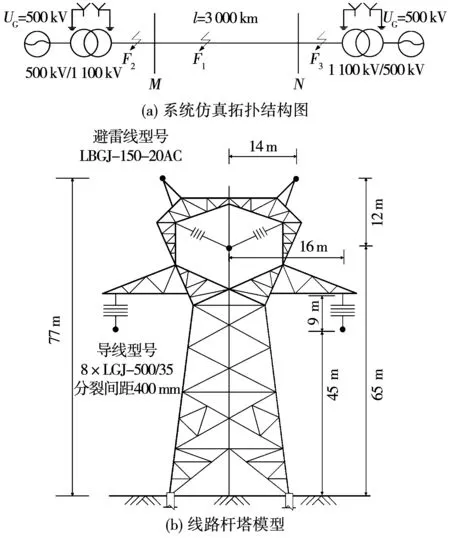
图9 系统仿真拓扑结构图Fig.9 System simulation topology structure diagram

由图10可知，由于行波在故障点和母线之间来回折反射，瞬时功率的正负极性在故障之后的变化并不恒定，这是由于零初始状态下能量在保护背侧系统中的储能元件之间发生了交换；瞬时功率对时间积分所求得的暂态能量极性确始终保持不变，则是因为其中的电阻上消耗的能量总是单调上升，且储能元件在故障后任一时刻都将存储着部分能量。

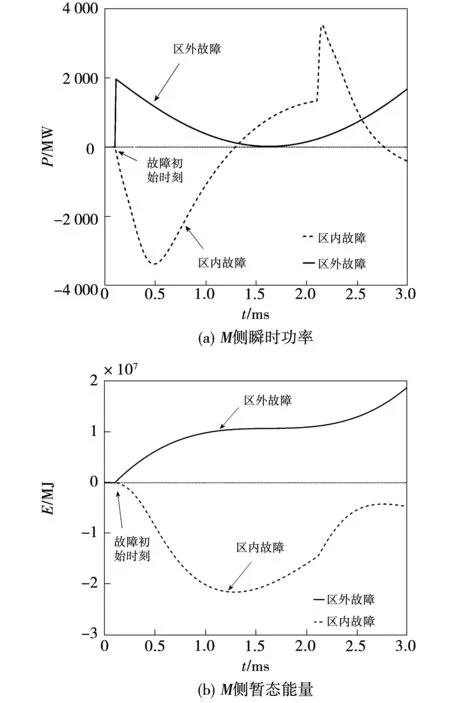
图10 M侧瞬时功率与暂态能量曲线Fig.10 Instantaneous power and transient energy curve on M-side

对于式(6)中积分时窗长而言，若Δt取得太小，可能会出现EM(t)在故障后t时间内尚未超过保护的阈值，有可能引起误判。由以上的分析可知，暂态能量函数的方向性在线路保护量测端背侧边界电路表现为纯电感或纯电容系统时，灵敏度最低。对于量测端背侧边界等值为纯电感情况来说，EM(t)故障后半周波内达到最大值；因此，本文中Δt取3 ms。

在图9所示的输电线路仿真系统中，分别在MN上距M端600 km、PM上以及NQ上发生故障时双端的暂态能量变化曲线分别如图11(a)、(b)、(c)所示。

积分时窗为3 ms下，当故障发生在被保护线路MN区内时，如图11(a)所示，M侧和N侧两端的暂态能量均小于0，根据式(11)，双端判别结果为区内故障；当故障发生在线路PM段时，如图11(b)所示，M侧暂态能量大于0而N侧暂态能量小于0，对于M侧而言，判别为反向故障，而N侧判别结果相反；同理，如图11(c)所示，当故障发生在线路NQ段时，M侧判为正向，而N侧判为反向。因此，由M、N双端方向继电器K1、K2可构成纵联保护决策表如表1所示。

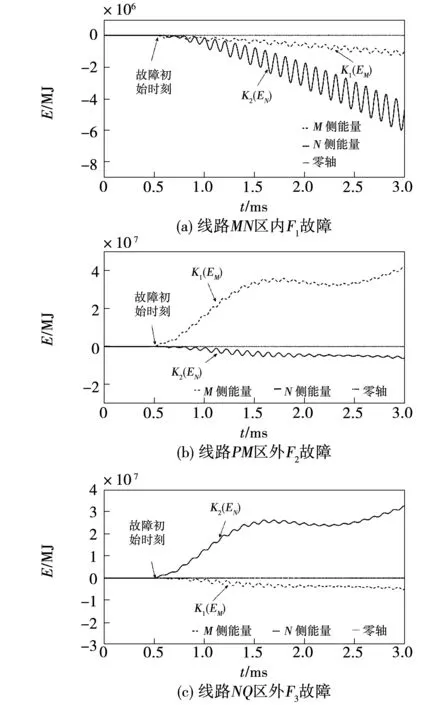
图11 在线路不同段发生故障时双端暂态能量变化曲线Fig.11 Transient energy curve of two ends when faults occur in different sections of circuit

表1 由方向继电器K1、K2构成的纵联保护决策表Table 1 Pilot protection decision table composed of directional relays K1 and K2

雷击故障是由于输电线路遭受雷击而导致线路杆塔绝缘子闪络造成的接地故障，但是由于雷击故障初始时刻是雷电流脉冲注入过程，造成绝缘子闪络引发单相接地，与普通的单相接地故障存在一定差异，此处将雷击故障单独进行仿真。线路保护区内MN发生雷击故障情况时，其暂态能量如图12所示，可以看出雷击故障造成的暂态能量值比普通接地故障更大，但是两侧能量值方向依旧保持一致，本文提出的暂态能量方向保护方法是可以使用的。

图12 线路MN上雷击故障Fig.12 Lightning fault on line MN

3.2 其他故障类型仿真分析

对于输电线路发生两相短路、两相短路接地及三相短路等复杂性故障时，从电路原理来说，其本质都是由故障点产生附加故障激励沿线路传播，引起母线处测量点采集到的故障分量发生变化，因此，对于暂态能量方向保护算法来说，无论故障类型如何，保护启动算法以及区内外故障判据始终适用。

假设半波长输电线路MN、母线M侧反方向PM和母线N侧反方向NQ上发生两相短路、两相短路接地与三相短路故障时，暂态能量分别如图13(a)、(b)、(c)所示。

由图13可知，半波长输电线路发生两相短路、两相短路接地以及三相短路故障时母线M、N测量点检测到的暂态能量大小与单相接地故障有所差别，但是暂态能量方向依旧满足本文所提出的区内外保护判据。对于半波长输电线路发生复杂性故障，其跳闸方案也与单相接地故障一致，都采用三相同时跳闸的方案，可见，暂态能量方向保护可以应对半波长输电线路发生的任何故障情况。

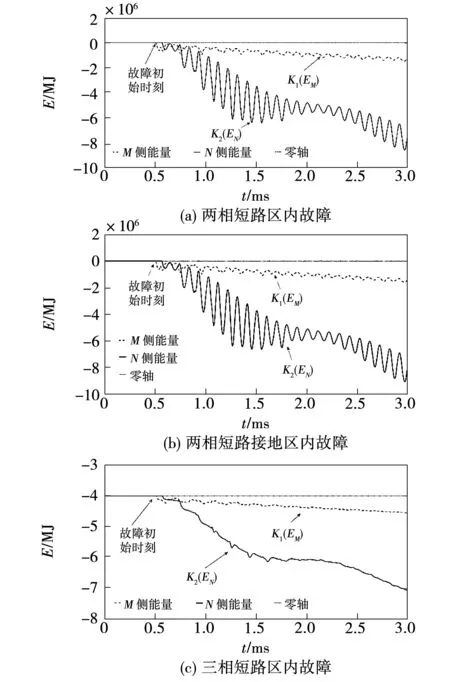
图13 不同故障类型时双端暂态能量变化曲线Fig.13 Transient energy curve of two ends under different fault conditions

3.3 故障距离、过渡电阻以及初始相角的影响

3.3.1 故障距离的影响

仍以图9所示仿真系统为例，M侧正方向线路MN段发生A相接地短路故障，短路电阻为10 Ω，故障初始角为60°，以100 km的增量对不同的故障位置进行仿真验证，在3 ms时窗内的暂态能量值随故障距离变化如图14所示。随着故障距离增大，区内故障的暂态能量绝对值会逐渐减小，但在末端故障时仍能可靠的识别正、反方向故障。

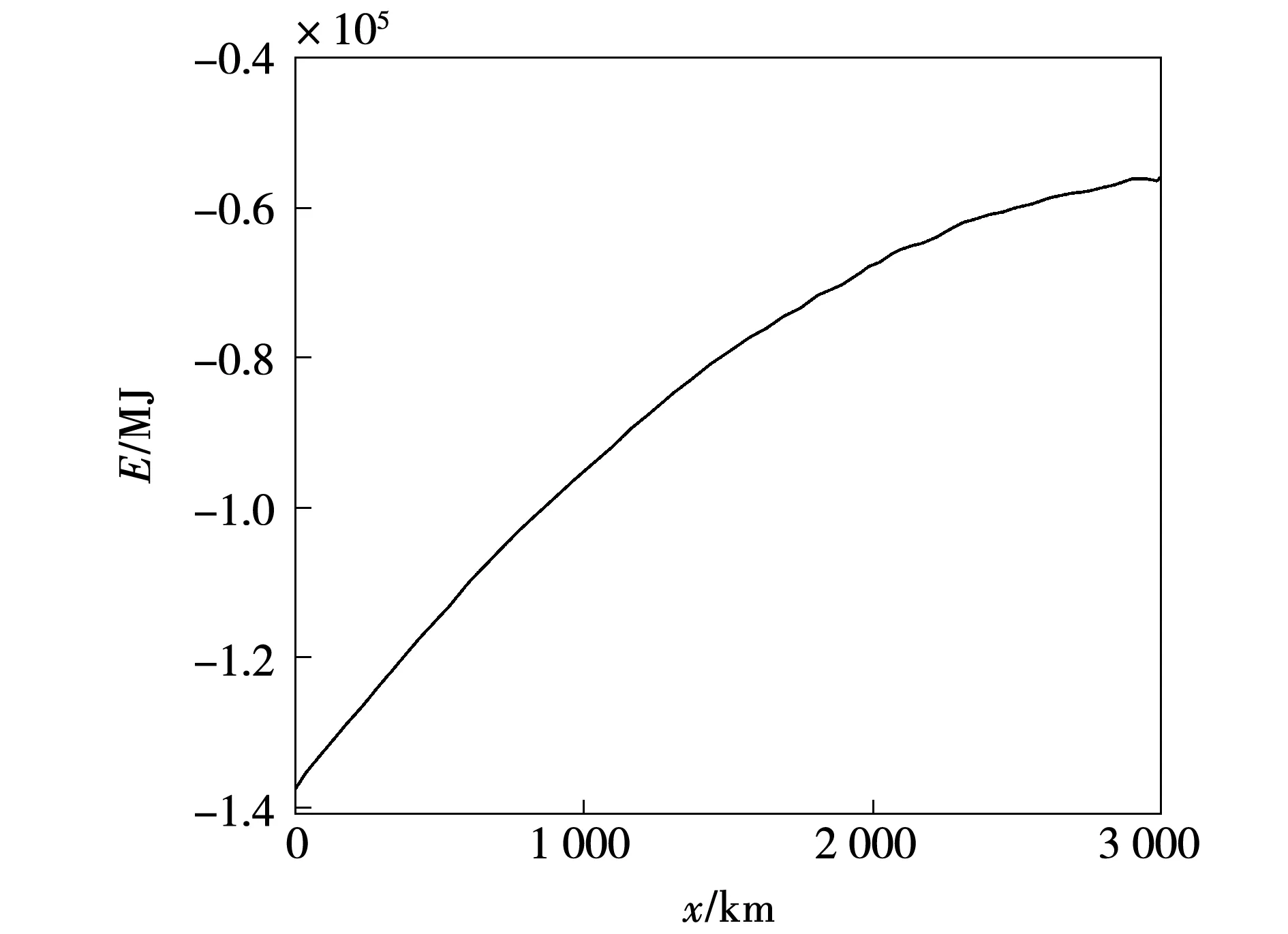
图14 暂态能量随故障距离的变化Fig.14 Changing curve of transient energy with fault distance

3.3.2 故障过渡电阻的影响

设在M侧正方向600 km处发生A相接地故障，故障初始角为60°，过渡电阻在0～300 Ω之间以30 Ω递增，M侧保护安装处检测到的暂态能量值如图15所示。随着过渡电阻的增大，暂态能量绝对值逐渐减小，但由于采用方向元件本质上是通过暂态能量的正负极性来判断正、反向故障，对暂态能量值的大小要求不高，且特高压输电网络中高阻故障发生情况极少，因此只需考虑躲过整定值并判别出极性即可，另一方面，由于暂态能量是瞬时功率的积分，在所选取的时窗内，能量的大小必能满足极性判断所需要求。

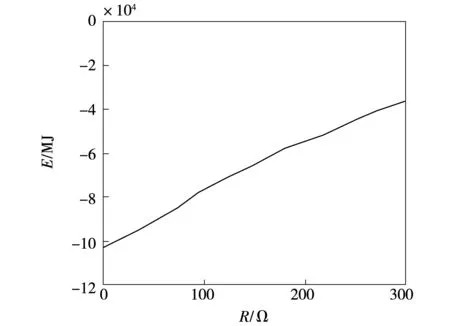
图15 暂态能量随故障过渡电阻的变化Fig.15 Changing curve of transient energy with transitional resistance

3.3.3 故障初始相角的影响

假设距M端正方向600 km处发生A相接地故障，过渡电阻为10 Ω，故障初始角在0～90°之间以每10°递增，M侧保护安装处检测到暂态能量值随故障初始角变化如图16所示。

由图16可知，由于暂态能量方向元件并不依赖初始行波波头极性，即使在故障初始角很小时，暂态能量的方向性仍旧明显，由此构成的方向元件灵敏度依旧很高。

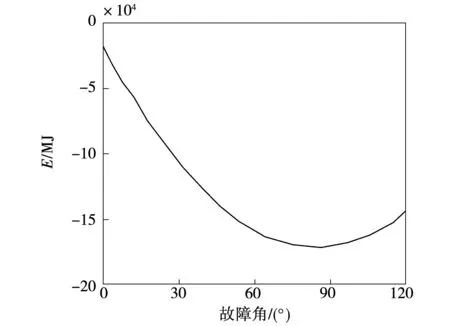
图16 暂态能量随故障初始角的变化Fig.16 Changing curve of transient energy with transitional resistance

4 结 论

半波长线路输电距离远，空间距离与电气距离不再呈线性且不单调，无法区分线路首端及正向末端出口故障，正向超越问题严重。本文针对常规保护无法适用于半波长线路的情况，提出一种基于暂态能量的半波长输电线路保护方案。该方案根据发生故障时测量端所取得的暂态电压电流计算瞬时功率以求得暂态能量，并根据暂态能量的正负极性判断故障发生在区内还是区外，可靠性、速动性好，PSCAD/EMTDC仿真结果证明该方法可在全线任意位置、任意故障角和过渡电阻的情况下有效实现区内、外故障辨识。