面向星表柔顺着陆的阻尼力可控电磁缓冲器设计

贾 山，高翔宇，陈金宝，尹 标

（1.南京航空航天大学航天学院，南京211106；2.深空星表探测机构技术工业和信息化部重点实验室，南京211106；3.航天进入减速与着陆技术实验室，南京211106）

人类航天事业的高速发展对深空星表探测技术和装备提出了越来越高的要求。叶培建院士等[1⁃2]多次提到软着陆技术与可移动着陆器在未来载人登陆、星表基地建设等任务中的重要性；路达等[3]也指出缓冲/行走一体化着陆器是未来开展高效星表作业必不可少的技术装备。

目前，用于星表软着陆的缓冲器主要有液压式、机械弹簧式、磁流变液式和溃缩吸能式[4⁃6]。溃缩吸能式中的铝蜂窝以其良好的力学性能和极高的可靠性成为现阶段最主流的缓冲材料。铝蜂窝压溃力基本为恒值[7⁃8]，在缓冲开始的时间节点存在加速度突变，降低落震冲击只能通过由弱到强的多级串联的方式实现[9]，这种结构的设计及参数确定都十分复杂[10]，也不能满足未来星表作业任务对可重复使用性的要求，更无法实现着陆后的调姿和移动。可见，传统的铝蜂窝缓冲器已经无法适应未来星表探测任务的多元性和灵活性[11]，研制可实现柔顺落震的吸能/驱动一体化缓冲装置已成为实现未来星表探测任务的基本前提，其中，电磁缓冲器以其吸能稳定性高、空间环境适应性好、阻尼系数连续可控等优点，有助于实现星表着陆过程的平顺性和可控性，在未来以载人着陆为代表的高可靠性任务中具有明显的应用价值。

针对上述需求，本文提出了一种可作为可复用/可调姿/可行走新型着陆器副缓冲支柱的阻尼特性可调电磁缓冲器。在结构上，通过将能耗电阻和缓冲器内/外筒之间滑动导杆的集成设计，在改善了低相对速度下电磁阻尼力弱的问题的同时，实现了落震过程中电磁阻尼力的被动平滑变化，降低了着陆瞬间的加速度，使落震过程相较于传统缓冲方式更加柔顺，且分别通过ANSYS 和Adams 软件的仿真，验证了基于新型着陆器落震动力学分析得出的（作为副缓冲支柱的）电磁缓冲器所应满足的主要性能指标和结构参数的正确性，并确定了其能耗电阻、励磁电流等关键电性参数。该电磁缓冲器可有效降低着陆器触地瞬时冲击过载，提高落震过程柔顺性，为未来新型着陆器研制提供了一种新的缓冲吸能解决方案。

1 采用电磁缓冲副支柱的新型着陆器

1.1 新型着陆器的构型设计和功能实现

为实现星表柔顺落震和可重复使用、可调姿/行走等功能，提出了如图1 所示的一种新型星表着陆缓冲机构。A 点与B 点安装有主缓冲器，采用旋转摩擦制动关节，自由度均为1；CD 杆表示充当辅助缓冲支柱的电磁缓冲器，在两端端点采用万向节连接。各关节初始角度以及各腿杆长度如表1 所示，其中，着陆器本体下表面距离足垫下端面的初始距离为0.6 m。

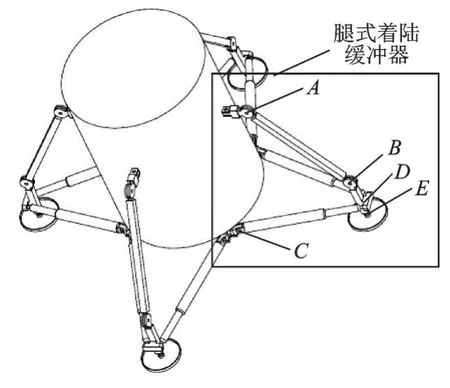
图1 着陆器模型Fig.1 Model of the lander

表1 着陆器主要构型参数Table 1 Main configuration parameters of the lander

该新型着陆器的缓冲功能主要由摩擦制动关节和电磁缓冲支柱协同实现，其中本文主要介绍电磁缓冲支柱的设计，摩擦制动关节的相关内容不做赘述。后续可以在主缓冲器摩擦制动关节处设置电机，并将作为副缓冲器的电磁缓冲器反向利用为直线电机，以此实现新型着陆缓冲机构的星表调姿、行走等功能，实现缓冲/行走一体化。

1.2 着陆过程简化模型的建立和分析

假设着陆天体为月球，探测器经制动火箭减速和自由落体式下降后接触月面的初速度（着陆过程初速度）为0.3 m/s（合作方提出的性能指标）。现给出1/4 着陆模型如图2 所示，其中y 点为着陆器整体质心，高度约为2 000 mm。并给出式（1）所示质量初始条件。

图2 月面着陆过程简化模型Fig.2 Simplified model of landing on lunar

为使落震过程中的着陆器本体质心处加速度变化轨迹平滑柔顺，提出一种线性理想加速度变化过程，分别如式(2)和图3 所示。其中-1.63 m/s2即为方向竖直向下的（ge为 地 球 表 面 重 力 加速度）。

考虑约束条件与实际着陆情况，将着陆时间T（即本体速度衰减为0 的时刻）设定为0.3 s。

同时考虑速度初始条件v0=-0.3 m/s 及位置初始条件s0=2.006 m，可得着陆器本体质心期望的下降位移、速度、加速度与时间t 的关系式为

图2 所示的着陆器模型自由度较多，现将其简化为如图4 所示3 自由度三连杆模型，其中，M 为简化后着陆器质心，θ1～θ3为简化后各关节夹角。

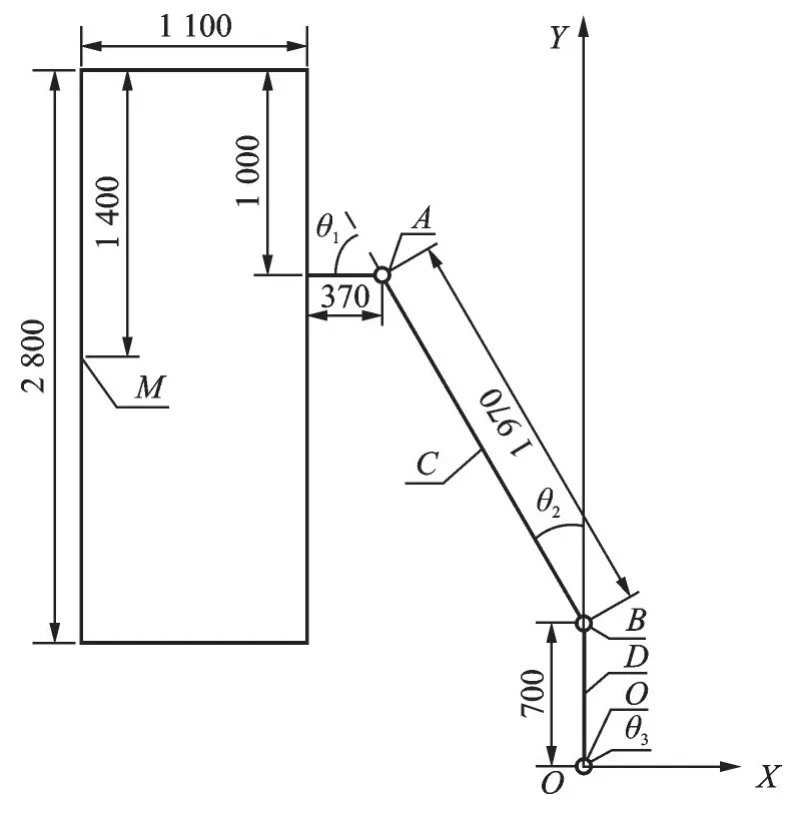
图4 着陆器简化模型Fig.4 Simplified model of the lander

利用式(3)所示的位移，速度以及加速度表达式进行逆运动学计算即可得到式(4)所示θ1～θ3表达式为

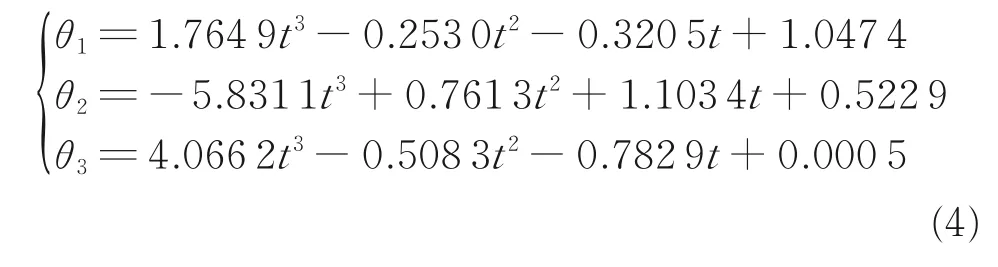
由于简化后模型有3 个自由度，故选择θ1～θ3作为拉氏建模的3 个广义坐标。依据式(3、4)进行拉氏建模，有

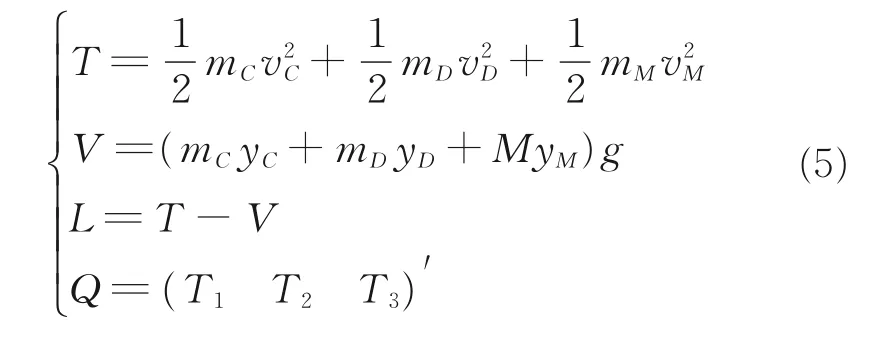
式中：T 为系统动能，V 为系统势能，L 为拉氏函数，Q 为对应3 个广义坐标的广义力，mC与mD分别代表杆C 与杆D 的质量，vC、vD与vM分别代表杆C、D 以及本体的速度，T1～T3为关节A、B、O 所提供的力矩，即简化过后着陆缓冲器输出要求，g 为月球表面重力加速度（其大小为1.63 m/s2）。

将已知量代入式(5)并将其代入拉氏方程即可求得T1～T3与时间的关系式并进行三次拟合得

将求得简化后的各关节输出力矩进行等效受力分析，设等效前后受力情况及各未知量定义如图5 所示。

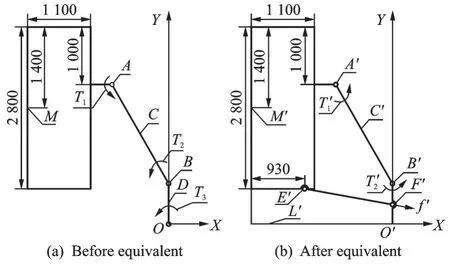
图5 等效模型以及未知量定义Fig.5 Equivalent model and definition of unknown quantity

图中：T1～T3分别为本体、大腿杆、小腿杆所受到的由3 个关节提供的力矩；T′1,T′2为大腿杆、小腿杆所受到的分别由A′点与B′点的主缓冲器提供的力矩；f′为副缓冲器E′F′提供给小腿杆的缓冲力。在等效后的模型中，O′点由铰连变为足垫，L′点为阻力与支持力的等效作用点，即模型整体的零力矩点。各缓冲力及力矩正方向如图5 所示进行定义。

利用受力分析的方法对零力矩点进行求解，并根据逆运动学计算得到的副缓冲器相对速度与时间关系式定义副缓冲器在XY 平面输出力与时间关系的表达式及曲线分别如式(7)和图6 所示。

f′=-31 517×(-3.15x2+0.28x+0.19) (7)

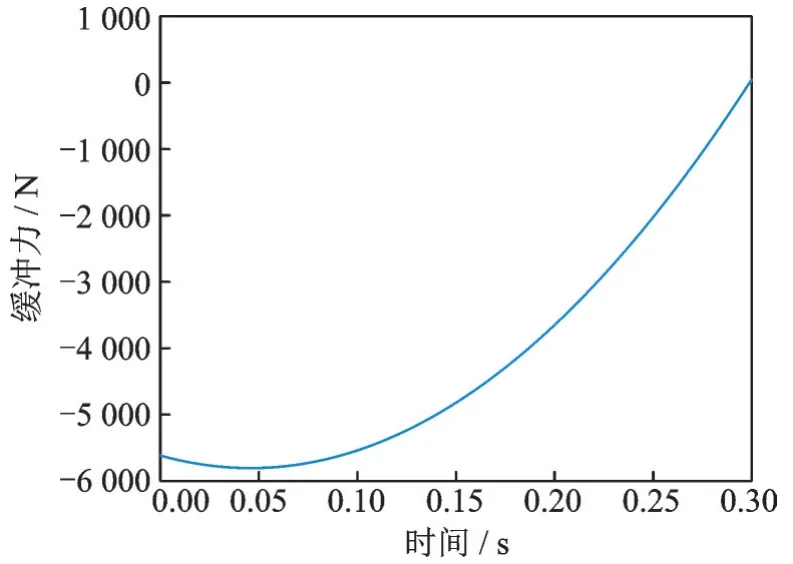
图6 副缓冲器输出阻尼力与时间关系曲线Fig.6 Relation curve between damping force and time of the secondary buffer

将已知量代入等效方程即可求得等效后如图7 所示髋关节(T′1)与膝关节(T′2)的理论输出。其中，髋关节与膝关节定义在图2 中已给出。

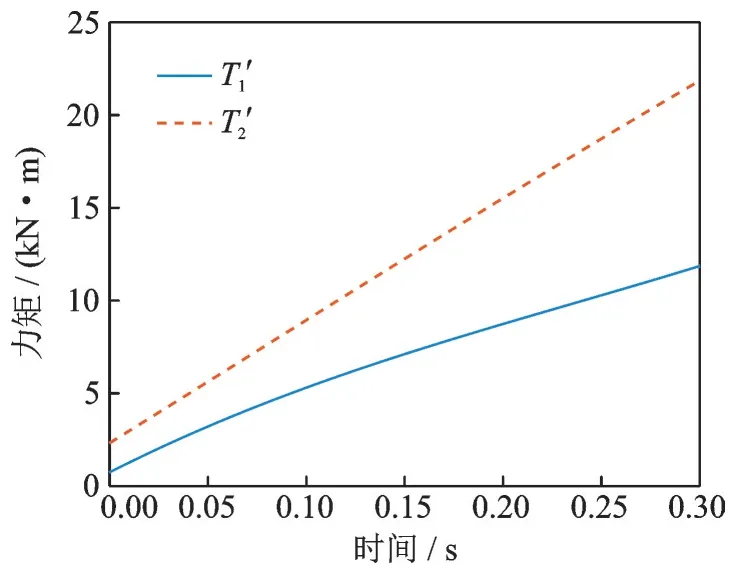
图7 等效结果Fig.7 Equivalent result

从图7 中可以看出，着陆器膝关节缓冲器相对于髋关节缓冲器整体需要更大的力矩，且髋关节输出扭矩最大约为12 000 N·m，膝关节输出最大扭矩约为22 000 N·m，二者趋势均为从小变大。

1.3 电磁缓冲器的性能指标和结构参数

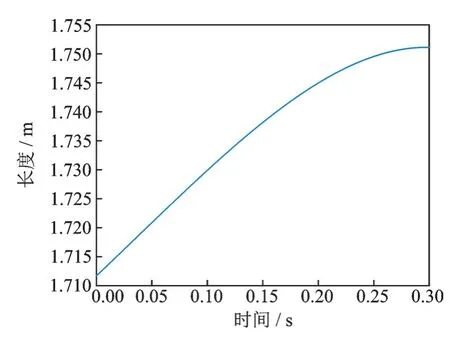
图8 电磁缓冲器长度变化曲线Fig.8 Length curve of electromagnetic buffer

图9 单个电磁缓冲器输出力曲线Fig.9 Force curve of single electromagnetic buffer

根据1.2 节所求得的θ1～θ3与时间t 的关系式推出在图5 中等效后模型E′F′之间距离与时间关系式，并据此给出图8 所示在四足同时落震时单个电磁缓冲器工作行程曲线。同时，假设输出缓冲力与时间成正比关系，得出图9 所示输出缓冲力与时间的关系曲线。

由图8～9 可知：（1）电磁缓冲器最大缓冲力不到3 000 N，故将电磁缓冲器最大缓冲力设为3 000 N；（2）电磁缓冲器的最大行程约为45 mm，令安全裕度为1.5，故将电磁缓冲器可用工作行程设为70 mm，也即缓冲器整体的设计安全裕度为1.5。

2 阻尼可控电磁缓冲器设计

2.1 电磁缓冲器构型设计

图10 为本文所述阻尼可控电磁缓冲器的整机构型设计。该电磁缓冲器主要由内、外双层筒体及位于双层筒体之中的电磁组件等构成。在内筒外部有若干个沿周向均布的滑块，滑块外表面与外筒内表面重合，形成了外筒与内筒之间的滑动副；内筒相对于外筒轴向滑移导向作用的导杆由电阻丝缠绕制成，通过电阻丝缠绕的疏密度变化形成导杆沿轴向电阻值的非线性变化；内筒内部有一线圈载体，在其上下两部分均设有一个励磁线圈；在外筒内部的空腔内设置感应线圈，其内部设有一柱状导磁材料以最大限度利用励磁线圈产生的磁场。

图10 电磁缓冲器Fig.10 Electromagnetic buffer

2.2 电磁缓冲器工作机理

导杆为电阻值沿轴向呈非线性变化的光滑直杆，在为内/外筒之间的相对滑动提供导向作用的同时，充当感应电流能耗电阻，如图11 所示，导杆接触点两侧的电阻杆并联接入感应线圈电路中。导杆的电阻值分布在假设电源放电为短时间恒电流的情况下由期望的落震时间、超级电容容量及电压、期望落震加速度曲线等共同确定。励磁线圈则通过线圈载体与内筒内部电路与外挂在缓冲器外侧的电容组件连接并形成闭合回路。

在开始进行着陆缓冲之前，内部组件相对位置如图11 所示，接触点位置在导杆正中间。缓冲过程中，使用电容组件给励磁线圈供电，内、外筒之间的相对运动使得感应线圈切割磁感线，同时，内筒与外筒的相对位置发生变化，改变了图11 中接触点的位置，改变接入能耗电路中的电阻大小，从而实现柔顺落震所需缓冲力的被动可控。单个导杆接入电路随接触点位置变化的关系式为

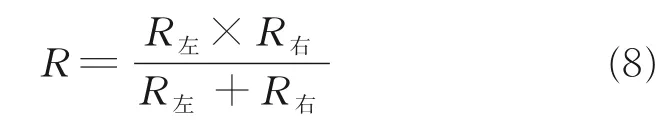
式中：R左为图11 中接触点左方导杆电阻值，R右为图11 中接触点右方导杆电阻值，其值跟随接触点位置变化而变化，从而实现了通过电阻导杆电阻分布被动控制电磁缓冲器输出力的柔顺变化。

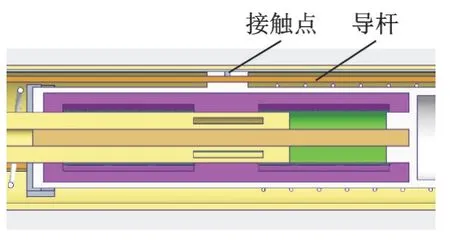
图11 电磁缓冲器剖面图Fig.11 Profile of electromagnetic buffer

2.3 电磁缓冲器参数确定

如前所述，电磁缓冲器的有效工作行程为70 mm，故确定励磁线圈螺线管长度为70 mm。考虑通过励磁线圈的电流为瞬时大电流，选取直径为0.5 mm 的导线，考虑导线要经过绝缘处理，选择利用单层绕线的方式绕100 匝。导磁材料则选择国际通用软磁材料1j22 铁钴合金，其磁饱和度为2.4 T,符合感应要求。对于感应线圈，考虑其需要尽量贴近励磁线圈，同时需要被励磁线圈完全包络以产生更大的感应电流，将其长度设定为40 mm，为加大其感应电流，考虑利用多层绕线的方式绕200～300 匝。

综上，可确定励磁线圈和感应线圈的参数如表2 所示。

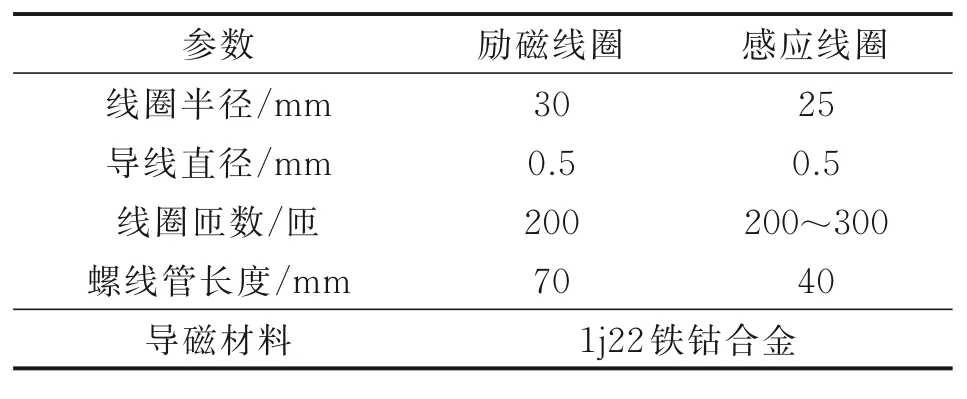
表2 励磁线圈及感应线圈参数Table 2 Parameters of excitation coil and induction coil

从表2 可解得励磁线圈磁感应强度以及感应线圈的电阻及有效长度为

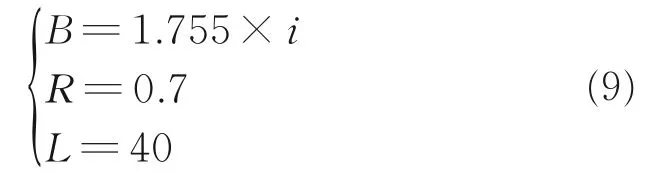
式中：i 为电流，R 为导线电阻，L 为导线总长度。

3 ANSYS 仿真验证

根据表2 所示参数，对电磁缓冲器电磁部分进行有限元仿真。

3.1 仿真初始设置

由于本模型中电磁元器件均处在同一平面内，故利用Maxwell 2D 软件进行分析。先在软件中进行如图12 所示建模。图中：A、B 为励磁线圈，为半径0.03 m、长0.07 m 的200 匝铜线圈；C 为感应线圈，为半径0.025 m、长0.04 m 的250 匝铜线圈，采用多层绕线方式；D 为导磁材料，仅中心柱状部分发挥作用，外侧包络的作用为限制磁场边界。

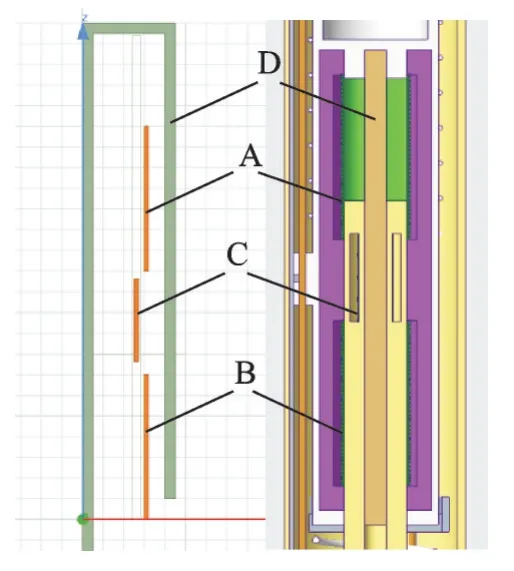
图12 仿真模型Fig.12 Simulation model

添加如图13 所示电路并将其导入仿真模型。图13 中，LWindingA1 与LWindingA2 分 别 对 应 图12 中A、B 励磁线圈，LWindingB 对应图12 中C 感应线圈，图中两励磁线圈供电的电容器件规格均为80 mF、1.4 kV。

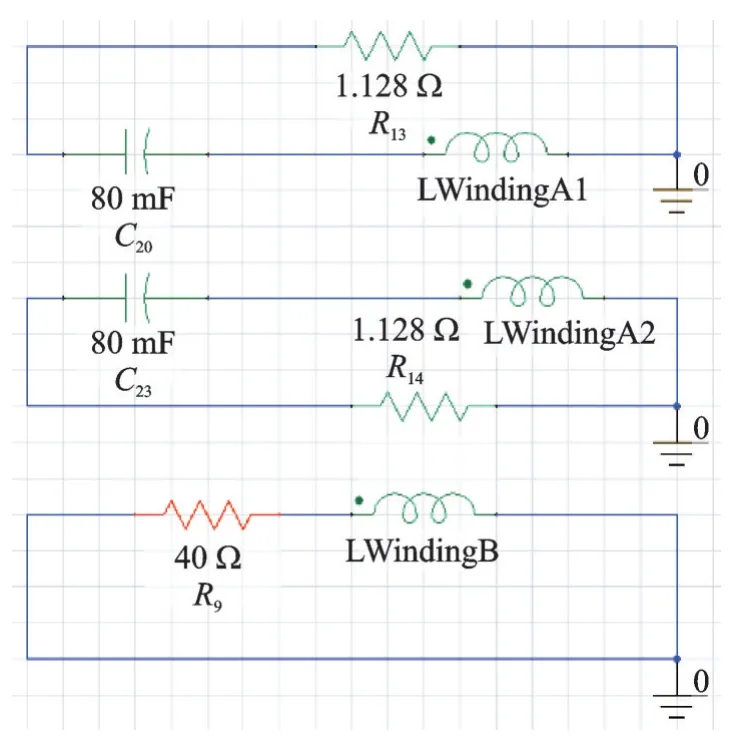
图13 ANSYS 电路Fig.13 Circuit in ANSYS

对感应线圈运动区域设置Boundary，并对其依照图8 所示电磁缓冲器长度变化曲线进行近似运动设置，如图14 所示。

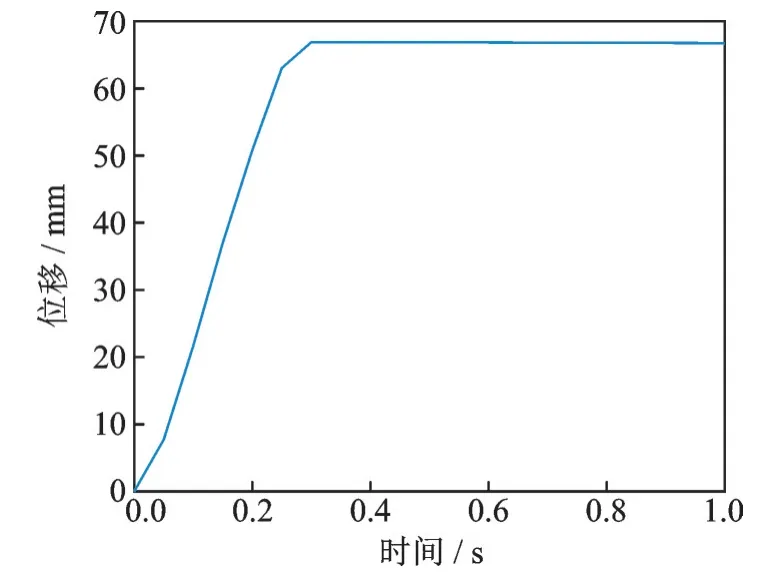
图14 ANSYS 中设置的位移曲线Fig.14 Set of displacement in ANSYS

利用MATLAB 软件根据位移曲线进行电阻导杆电阻分配求解。导电滑块与电阻导杆的初始接触点为导杆正中间，单边行程为0.07 m，且在行程内电阻均匀分布，初始串联电阻为40 Ω，则可绘制出图15 中与感应线圈串联电阻R9的变化趋势并将其输入Maxwell 电路。

图15 导杆能耗电阻接入电路大小趋势Fig.15 Trend chart of energy consumption resistance ac⁃cess circuit of guide rod

最后，设置测量参数为励磁线圈受到的力，并将仿真步长设置为0.05 s，设置仿真边界并进行仿真。

3.2 仿真结果

利用3.1 节中的仿真初始条件进行仿真，可得到励磁电流与感应电流曲线如图16 所示。

从图16 中可看出超级电容放电在0.05 s 时到达最高峰，整体有效放电时间约持续0.4 s，最大瞬时励磁电流可达到约770 A，持续放电时间满足0.3 s 的落震需求。

对仿真所得数据进行平滑处理后，可得到如图17 所示感应线圈受力曲线。

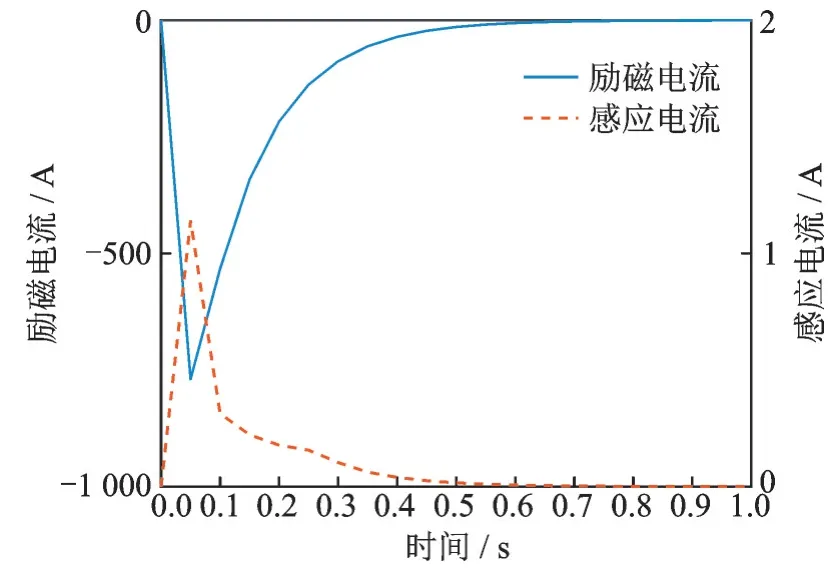
图16 仿真电流曲线Fig.16 Current curves in simulation

图17 感应线圈受力曲线Fig.17 Force curve of induction coil

4 Adams 仿真验证

为验证1.3 节中计算得到的着陆器主、副缓冲器的性能参数正确性，进行了基于Adams 的刚体动力学仿真。

4.1 仿真初始设置

依据所提出的性能指标，给出如表3 所示的两种仿真工况。

表3 不同工况落震仿真Table 3 Simulation parameters of different falling con⁃ditions

将图1 所示的着陆器模型导入Adams 软件中，并依据1.3 节中计算所得各项参数，将副缓冲器所对应的移动副预紧力设置为3 000 N、髋关节及膝关节对应的转动副预紧力设置为7 000 N、足垫与月面间的等效摩擦因数为0.5。分别对两种工况进行时长5 s、步长为0.01 s 的仿真。

4.2 仿真结果与参数确定

利用4.1 节中的仿真初始条件进行仿真，即可得到两种工况下副缓冲器受力曲线分别如图18～20 所示。

在工况1 中，着陆器整体受力对称，安装在着陆器上的8 个副缓冲器受力情况基本一致，其平滑后的缓冲力曲线如图18 所示；在工况2 中，采用“1⁃2⁃1”落震方式，即一条腿先与月面进行接触缓冲，另外3 条腿后与月面进行接触缓冲，图19 即为先与月面接触着陆腿副缓冲器受力图，图20 为后与月面接触着陆腿副缓冲器受力图。

由图18 可知：着陆器约0.5 s 完成缓冲，且副缓冲器输出最大阻尼力约为3 000 N，与理论计算基本一致。

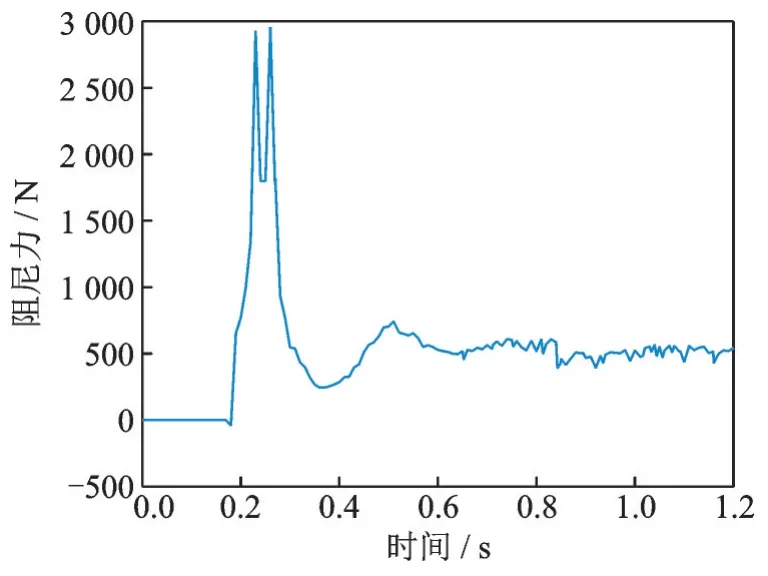
图18 工况1 副缓冲器受力图Fig.18 Force diagram of secondary buffer under condition 1

由图19，20 可知：先触地着陆腿分为两个峰值，一个峰值在先触地着陆腿落地时，另一个峰值在后触地着陆腿落地时，两次峰值大小相差约1 000 N，但是方向相反，结合缓冲器运动情况，考虑先触地着陆腿上副缓冲器应该是处于先压缩、后拉伸的状态；后触地着陆腿上副缓冲器仅在后触地着陆腿落地时有一次峰值，即仅被拉伸。此外，工况2 下，先触地和后触地的副缓冲器所提供的最大缓冲力均不超过3 000 N。

图19 工况2 先触地着陆腿副缓冲器受力图Fig.19 Force diagram of secondary buffer of the first touch⁃down-leg under condition 2

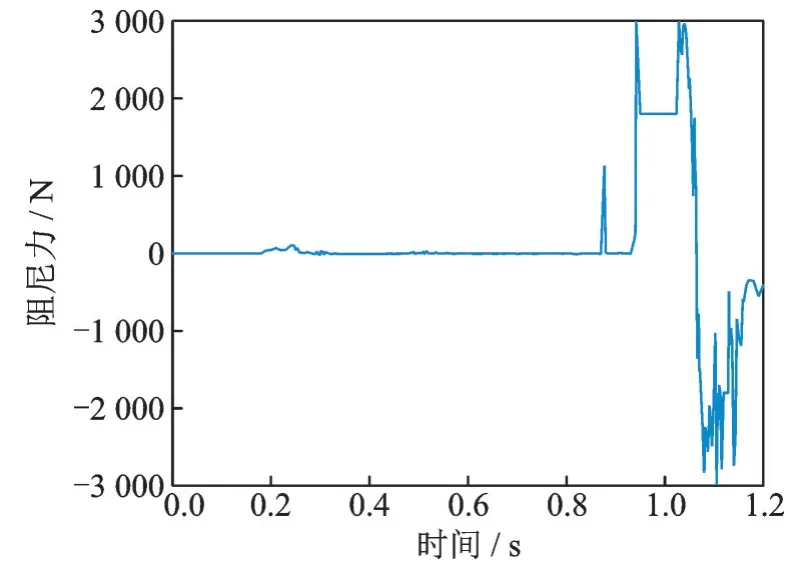
图20 工况2 后触地着陆腿副缓冲器受力图Fig.20 Force diagram of secondary buffer of the rear touch⁃down-leg under condition 2

图21 为工况2 中与图17 相对应的副缓冲器输出阻尼力的对比图，可知：分别在ANSYS 和Ad⁃ams 中获得的副缓冲器电磁缓冲力的最大值、变化规律和持续时间均较为相似，其中Adams 软件由于对着陆器进行仿真，各部件间会相互影响，从而出现振荡，故该振荡可以忽略不计。综上所述，可以依据仿真结果确定电磁缓冲器的主要设计参数，如表4 所示。

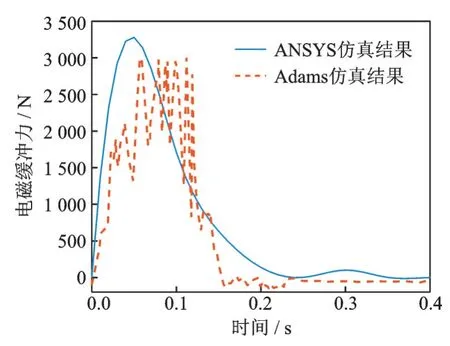
图21 不同仿真环境下的电磁缓冲力对比Fig.21 Comparison between the electromagnetic buffer forces under different simulation environments

表4 电磁缓冲器的主要设计参数Table 4 Key parameters of electromagnetic buffer

5 结 论

本文面向未来深空星表探测领域对柔顺着陆缓冲装置的需求，提出了一种可作为可复用/可调姿/可行走新型着陆器副缓冲支柱的阻尼特性可调电磁缓冲器。在结构设计上，该电磁缓冲器创新性地提出了通过滑动电阻导杆实现电磁阻尼力随缓冲行程从小至大的被动调节，对比于传统铝蜂窝缓冲减少了在着陆瞬间的加速度突变，且通过新型着陆器落震动力学分析得出了作为副缓冲支柱的电磁缓冲器所应满足的主要性能指标和结构参数，并分别在ANSYS 和Adams 环境下完成了虚拟样机建模与仿真，验证了电磁缓冲器的功能有效性，并确定了能耗电阻、励磁电流等关键电性参数。作为副缓冲支柱，该电磁缓冲器可有效降低着陆器触地瞬时冲击过载，提高落震过程柔顺性，为未来新型着陆器的研制提供了一种新的缓冲吸能解决方案。