纤维金属层板层间应力理论模型及实验验证
2021-03-31赵国庆湛利华吴欣桐关成龙戴光明
赵国庆,湛利华,吴欣桐,关成龙,戴光明
(1.中南大学机电工程学院,长沙410083;2.中南大学轻合金研究院,长沙410083)
纤维金属层板是由纤维增强复合材料和金属薄板交替铺层后经一定的温度和压力环境作用固化成型的一类新型超混合复合材料[1⁃3]。制件在成型时处于一个温度和压力随时间变化的过程中。由于在任一方向上组分材料的热膨胀系数和模量都有差异,当异质界面形成后,这种差异会通过界面对纤维复合材料和金属层发生作用,从而在制件的层间产生层间应力[4]。此外,纤维金属层板的纤维桥接作用,虽然降低了裂纹扩展的速率,但又使其在界面处产生层间剪切应力从而使得层板出现分层扩展[5⁃9]。若由于组分材料的差异、制件所处服役环境以及其他元素的综合作用使得最大层间应力超过临界值,纤维金属层板可能会出现分层,开裂或剥离等危险状况导致重大事故,危及人生和财产安全。因此,必须要开展对纤维金属层板层间应力状态的理论研究,揭示纤维金属层板层间应力的分布规律。
现有研究中,瞿尔仁等[10]对纤维增强复合材料(Fiber reinforced polymer,FRP)加固混凝土梁的层间应力进行了分析,建立了其弹塑性方程。刘祖华和朱伯龙[11]研究了3 种载荷下粘钢加固混凝土梁的层间应力,并给出了解析解。邓军和黄培彦[12]研究了碳纤维增强复合材料(Carbon fibre⁃re⁃inforced polymer,CFRP)加固钢梁的界面,获得了界面应力表达式。Deng 等[13]研究了CFRP 加固钢梁端部应力集中,提出了一种计算层间应力的解析解方法,并将该方法推广到端部为锥形的CFRP 板上,可以显著降低应力集中,并用有限元进行了验证。王昌昊等[14]用有限元模拟的方式模分析了不同铺层的Glare 层板的层间应力曲线。李宏运和胡宏军[15]以及徐凤娟等[16]都介绍了一种纤维金属层板残余应力的解析计算方法。Lin 等[17]运用实验和理论分析的方法研究了碳纤维铝合金层板的热残余应变。张培新和李亚智[18]运用两种有限元建模方法,使用重合节点描述层间,对复合材料的层间应力进行研究。张福范[19]分别用正弦级数和余弦级数表达层间剪应力和层间正应力分量,用级数求和和能量法原理,最终得到复合材料层间剪应力和层间正应力的表达式。
而对于纤维金属层板的层间应力的理论研究目前较少,因此本文以现有的关于异质界面层间应力的求解方法为基础,推导出了关于纤维金属层板层间应力的公式。
1 模型建立
1.1 力学模型的简化
本文对于层间应力模型的建立,首先是探究简单非对称单向铺层的应力模型,然后分析简单非对称铺层与标准对称铺层之间的关系,从而将非对称铺层应力模型推广到任意标准对称铺层中。
为简化非对称铺层模型,通过设置3 组实验,分别探究非对称铺层制件的纵向尺度(沿纤维方向)、横向尺度(垂直纤维方向)和复合材料体积分数对于制件脱模后挠曲程度的影响规律,反映出三维各向尺度效应与层间应力的影响关系,从而合理简化力学模型来分析并建立层间应力的理论解析模型。
实验所用复合材料为美国Cytee 公司的T800/X850 预浸料,单层厚度为0.188 mm;所用铝合金为东北轻合金的2024⁃T3 薄板,单层厚度为0.3 mm。实验流程为3 组实验的制件成型,用ATOS 三维扫描仪扫描,最终综合分析,从而得出结论。
3 组实验分别重复3 次实验。用曲率来表示制件的挠曲程度,分别得非对称铺层制件挠曲曲率与制件纵向尺度、横向尺度和复合材料占比的关联规律。实验试件信息如表1 所示,实验结果如图1~3所示。

表1 实验试件铺层与尺寸信息Table 1 Test specimen layering and dimension informa⁃tion
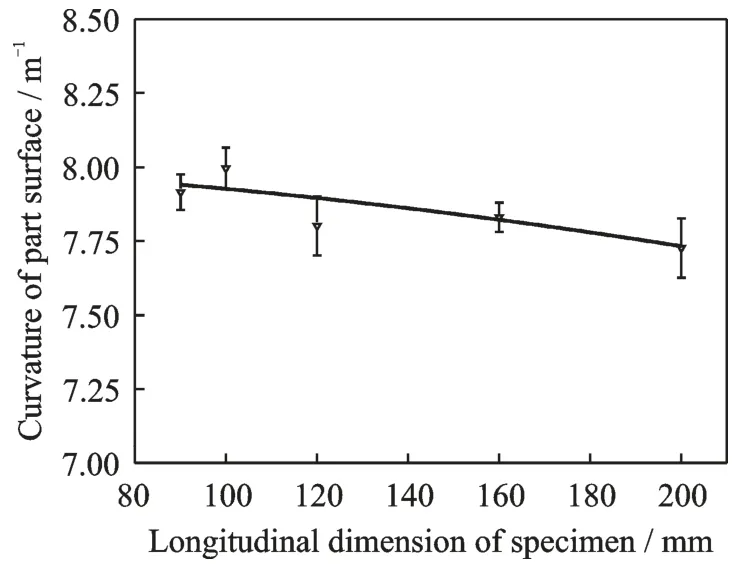
图1 非对称铺层制件挠曲曲率与制件纵向尺度的关联规律Fig.1 Relationship between flexural curvature and longitu⁃dinal dimension of asymmetric layering parts

图2 非对称铺层制件挠曲曲率与制件横向尺度的关联规律Fig.2 Relationship between flexural curvature and trans⁃verse dimension of asymmetric layering parts
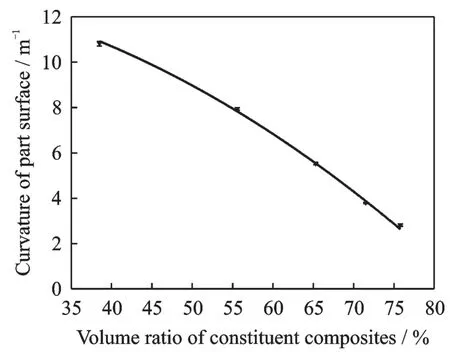
图3 非对称铺层制件挠曲曲率与制件复合材料体积占比关联规律Fig.3 Relationship between flexural curvature and volume ratio of composite materials of asymmetric layering parts
从实验结果来看,不同纵向尺度非对称铺层制件变形后的拟合圆柱直径基本稳定在250~258 mm 之间,其制件平均曲率为7.90 m-1。不同横向尺度非对称铺层制件变形后的拟合圆柱直径基本稳定在243~254 mm 之间,其制件平均曲率为8 m-1,因此纤维金属层板非对称铺层制件的纵向尺度和横向尺度效应对于制件的变形影响并不是很大。而不同复合材料占比的非对称铺层制件的拟合圆柱直径从180~718 mm 不等,曲率从2.8~11 不等。不同复合材料体积占比的制件,其挠曲曲率变化明显,从图3 中拟合结果可知,制件挠曲曲率ρ 与制件复合材料体积占比VCFRP的近似关联规律为

基于以上结论,纤维金属层板层间应力理论建模时,可以将三维问题简化为垂直于横向尺度平面内的二维问题。即对于单向铺层的制件,将制件简化为以沿纤维方向为长度方向,而以金属层板平面的法线方向为厚度方向的二维制件,直接研究该平面内层间界面的受力问题。
1.2 非对称铺层层间应力理论模型
对最基本的非对称铺层模型,参考已经商业化的纤维金属层板铺层,金属/纤维增强复合材料胶接副中复合材料最小铺层为2 层,即首选Al/[CFRP]2进行理论分析。将制件简化到二维平面,同时为了简化计算,理论几何模型中,在金属层与复合材料之间引入粘结层,用于传递层间应力。实际制件中,该粘结层为复合材料与金属之间的预浸料树脂层。
取制件微段dx(x 轴为图4 所示沿纤维方向)对其受力分析。粘结层为复合材料层分离出来的树脂层,厚度极小,其热效应综合到复合材料层中考虑,故忽略粘结层的轴力和剪力。
图4 为纤维金属层板层间应力分析模型。N为微段所受轴力,Q 为剪力,M 为弯矩,1 代表金属层,厚度为h1,2 代表复合材料层,厚度为h2,a 代表粘结层,厚度为ta。层板宽度为b,微段长dx。
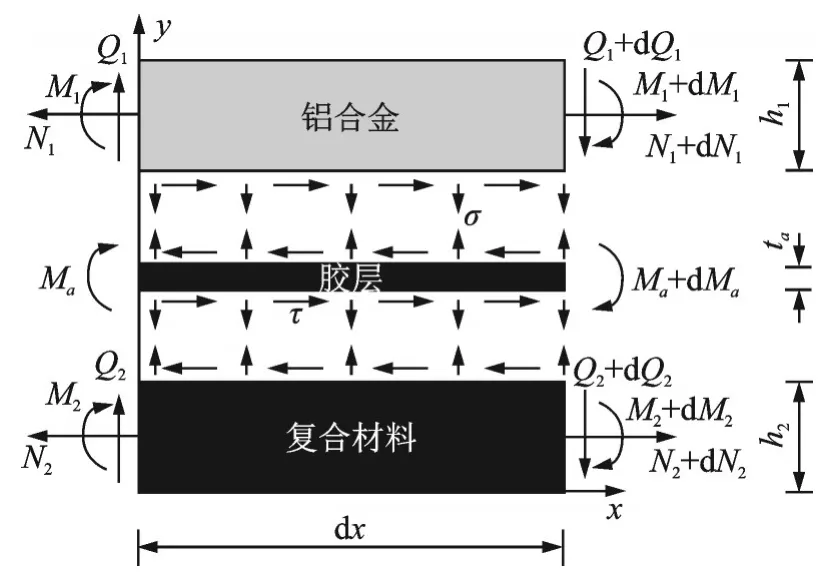
图4 纤维金属层板非对称铺层制件受力分析模型规律Fig.4 Force analysis model for asymmetric laminates of fi⁃ber metal laminates
对金属层与复合材料层做受力分析,可得以下各式

对于由金属层、粘结层和复合材料层组成的组合截面受力分析,有

式中:M(x)为试件沿x 轴弯矩方程;Ma为粘结层弯矩,且

则式(10)变为
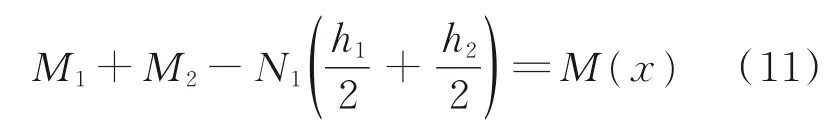
假设界面粘结牢固,则在距离纤维金属层板坐标原点为x 的某处,金属层的下表面与粘结层的上表面的纵向位移一致,记为u1,粘结层的下表面与复合材料的上表面纵向位移(沿x 轴方向)一致,记为u2,则有
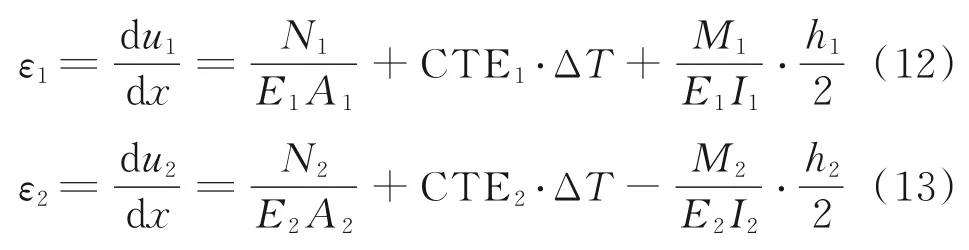
式中:E、A、I、CTE、ΔT 分别代表材料的弹性模量、横截表面积、横截面对x 轴的惯性矩、材料的热膨胀系数和温差。
同时假设粘结层为线性弹性体,并取u(x,y)和v(x,y)分别为粘接层任一位置沿x 轴向和y 轴向位移,则粘结层的剪应变γ 与剪应力τ 可分别表示为
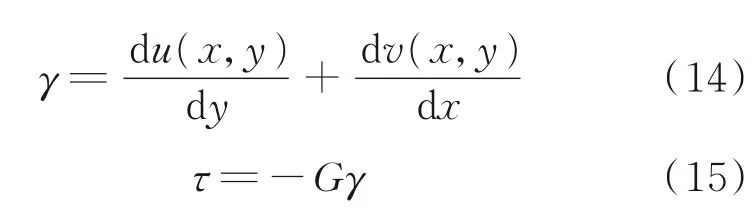
则


且粘结层很薄,可认为粘结层的剪应力不随胶层的厚度变化而变化,因此可以认为粘结层中的应变是线性的,有
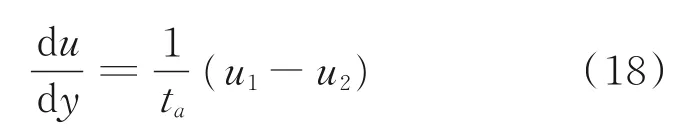
综合式(17),有
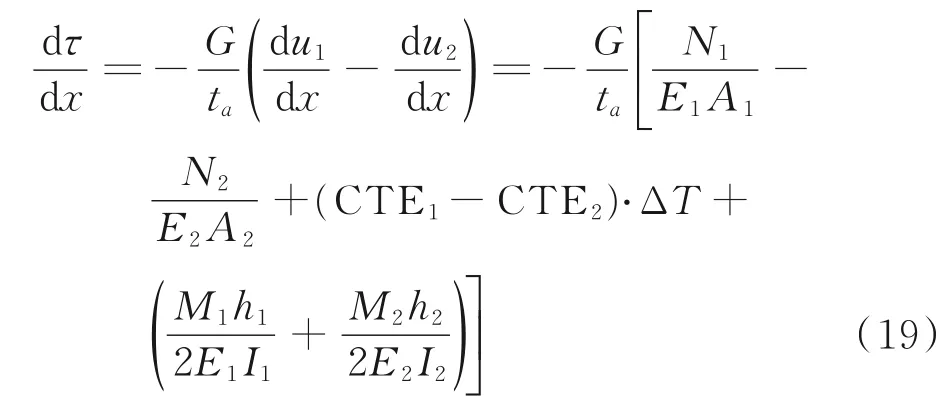
结合式(8),有

式中Q1(x)为延x 轴方向剪力的变化函数。
令式(20)中

则有
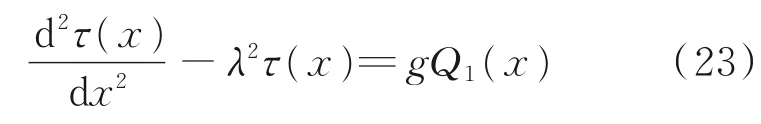
至此,层间剪应力问题转化为上式所示的二阶非齐次线性微分方程。接下来先求解Q1(x)。
Prussak 等[20]将残余应力的作用等效成一组施加在制件的轴力和弯矩。相似地,非对称铺层的制件在成形后,因变形协调,制件产生较大的曲率。而对成形后的制件反向施加相应的载荷使其与制件层间应力平衡,则非对称制件恢复到无翘曲状态。若将成形后的制件看作是一简支梁,对其施加一个合适的均布载荷,则可以实现弯曲的非对称制件重新变形为平板。因此,在该问题中,可以将层间应力造成非对称制件挠曲的物理模型等效为一承受均布载荷的简支梁。其中层合板成型后的最大挠度可以推导出,记为fmax,由材料力学知识,挠曲线方程与最大挠度为
式中:q 为均布载荷,L 为制件长度。
对于均布载荷简支梁,其弯矩和剪力方程为
将式(27)代入式(23),求解可得层间剪应力的通解为
考虑到纤维金属层板的横向对称性,即在x 轴方向的中点处,剪应力为零,可得
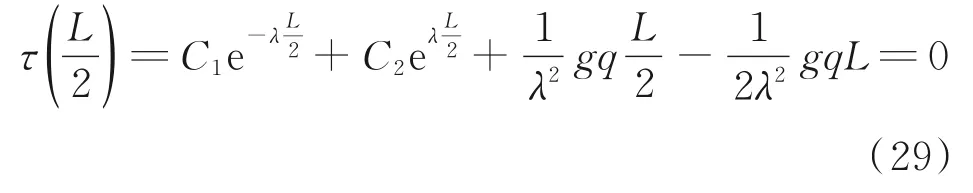
在制件的两端,轴力为零,可得

综 合 式(11,26,29,30),可 求 得C1和C2分别为
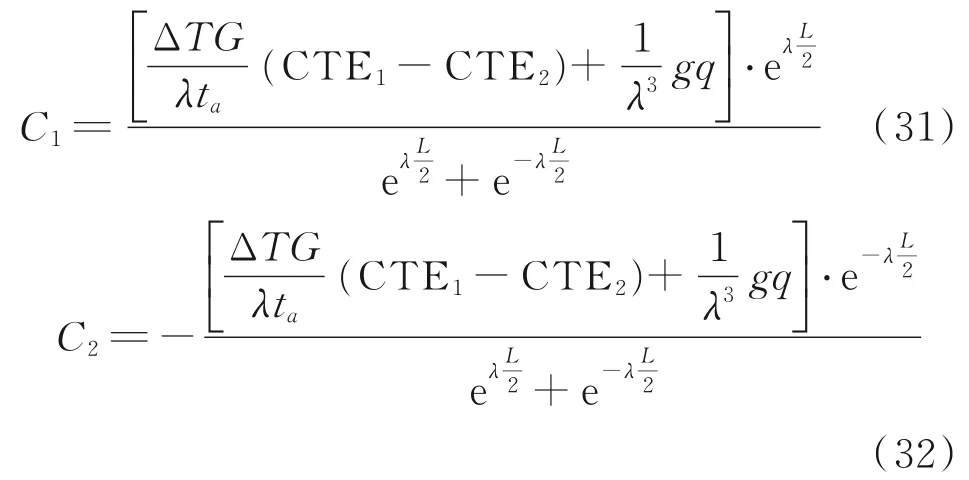
对于fmax,由图5 可知角β 与弧长L、挠曲半径R和最大挠度fmax的关系。
最大挠曲fmax与制件长度L 的关系为
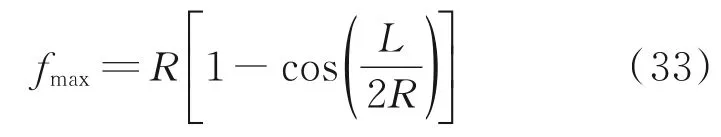
结合式(25),有

图5 非对称制件脱模后制件挠曲半径与最大挠度几何关系示意图Fig.5 Schematic diagram of geometric relationship between bending radius and maximum deflection of asymmet⁃ric parts after demoulding

综上推导,非对称铺层的纤维金属层板的层间剪应力表达式为

1.3 对称铺层层间应力理论模型
以图6 的标准4/3 铺层为例,可知任意标准铺层均可划分为偶数组非对称铺层。则各个非对称铺层同样可看成受均布载荷作用的结果。于是这里可以将对称铺层分为若干非对称铺层进行分析。
而1.2 节已经推出了非对称铺层的层间应力模型。将其简化为
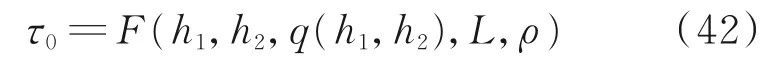

图6 标准4/3 铺层纤维金属层板简图Fig.6 Schematic diagram of standard 4/3 laminate fiber metal laminate
则易知
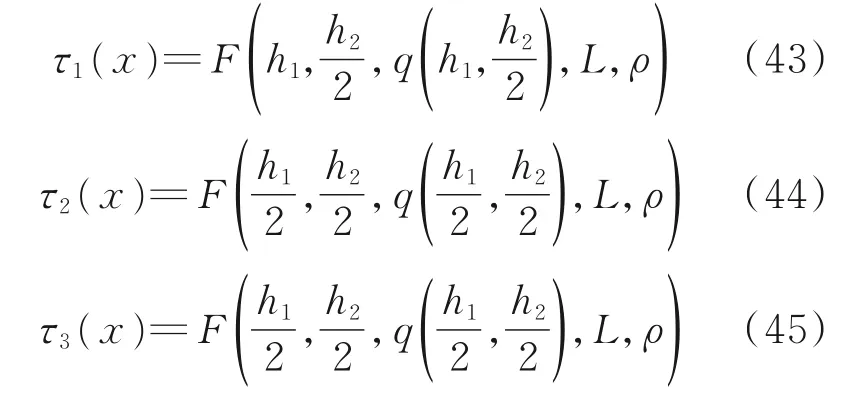
进一步可推知任意n+1/n 标准铺层的任一层间剪应力为

同样对标准4/3 铺层做受力分析,参考式(2~7),并推广至任意标准铺层,具体计算结果此处不再赘述。可得层间正应力与层间剪应力的关系式有

至此,标准铺层的纤维金属层板的层间应力理论模型建立完成,下面通过实验进行验证。
2 应力测试实验
2.1 实验材料及方法
使用1.5 mm 厚度的AA 2024⁃T3 铝合金与0.188 mm 厚度的T800/X850 单向预浸料为原材料。
实验设备为大连樱田YT⁃13⁃03 实验专用热压罐。层内正应力的采集系统为纤维金属层板成型过程多参数在线监测系统[21]。所用传感器为光纤布拉格光栅传感器(Fiber Bragg grating,FBG)和K 型热电偶。
由于无法直接测量纤维金属层板层间应力,本实验拟基于层间剪应力与层内正应力关系间接得出层内正应力的理论值,通过对比由层间剪应力转化到层内正应力理论值与实验值达到验证层间应力理论解析解准确性的目的。
为了方便后续实验的数据测量,这里只对图7的外层金属层进行受力分析,有
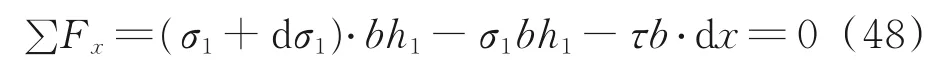
可得


图7 纤维金属层板2/1 铺层制件受力分析模型Fig.7 Force analysis model of fiber metal laminate 2/1 laminate
有

由边界条件,在制件端部σ1(x)=0 可得
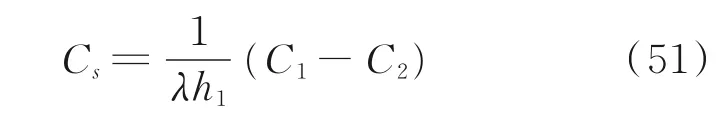
此时可采用如图8 所示的方式集中布置传感器(沿纤维方向埋放),并认为传感器测得值均能代表沿纵向尺度的分布规律,将测得的平均值与理论公式的曲线每一段相对应的平均值用做对比的方式验证理论解析解的准确性。

图8 实验传感器布置及真空袋构成Fig.8 Experimental sensor arrangement and vacuum bag composition
2.2 实验结果
6 个通道测得的制件残余应力分别为142.655、157.831、163.876、167.491、167.974 和167.203 MPa,即结束点时布置传感器的6 处层内正应力。
如图9 为超景深显微镜拍摄的制件胶层附近的形貌,测量三处胶层的厚度,求平均值得粘结层的厚度为0.195 mm。

图9 胶层附近区域形貌Fig.9 Area morphology of adhesive layer accessories
计算理论解析解还需用到材料的其他参数,由于目前公开的研究中,并没有给出T800/X850 复合材料的具体热力学参数,根据文献[22]的方法,采用体积法求得制件的参数如表2 所示。
根据上面的数据并结合式(35,48,51,52),可得层内正应力的理论公式
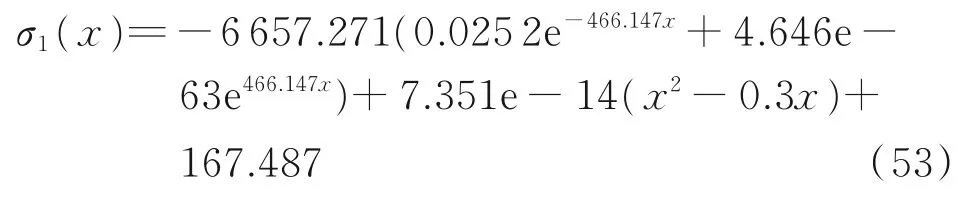
将实验所得数据与式(53)计算所得的理论层内正应力进行对比,结果如图10 所示。求得理论值相对于实验值的误差分别为3.504%、1.322%、0.617%、1.088%、0.716%和-0.169%。从实验结果可以看出:靠近层合板外侧的两处实验测得值与通过积分法求得的理论值相比较大,分析其主要原因是因为其位于制件最边缘处,此处铝合金层内正应力处于靠近零值,而传感器因为本身的长度较大,只能测得该区域的平均值,因此受传感器靠近中心部分的影响,该两处理论值小于实验值。其他各处实验测得值与理论值的积分法平均值相差较小。总体来看,理论解析值与实验测得值吻合较好,因此本文所得出的理论解析解能较为准确地描述纤维金属层板的层间应力。
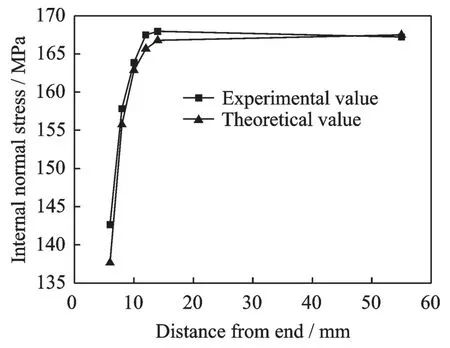
图10 层内正应力的实验测得值与理论转换值对比Fig.10 Comparison between experimental and theoretical values of normal stress in the layer
3 结 论
(1)本文以T800/X850 与2024 铝合金组成的层合板为例,得出了单向非对称铺层制件的挠曲变形程度主要与制件中金属与复合材料的占比有关。
(2)根据挠曲曲率与制件复合材料体积占比以及非对称铺层与标准对称铺层的关系,得出了非对称铺层制件层间应力的数学表达式,并推广到了标准单向对称铺层制件的层间应力理论模型中。
(3)结合光纤光栅传感器,经过实验检验,本文的理论模型预测的应力大小与实测应力大小达到了良好的一致性,最大偏差为3.504%。
