考虑弹性变形的月面表取机械臂精度补偿方法
2021-03-31孙丰磊
陈 钢,孙丰磊,李 彤,邵 文
(北京邮电大学自动化学院,北京100876)
月球是距离地球最近的天体,是人类进行深空 探测的前沿阵地,对月球的研究将促进人类对月球、地外行星乃至太阳系的认识。月壤采样返回是中国探月工程“绕、落、回”三部曲的最终章[1]。空间机械臂具有技术成熟、灵活性好等优点,适合代替人类执行采样任务[2]。表取机械臂是空间机械臂的一个重要分支,在月球表面采样工作中,表取机械臂的任务是多次抓取月球表面的月壤并倾泻到采样封装装置中,采样结束后,提取采样封装装置,将其转移到返回舱。机械臂末端绝对定位精度决定了表取机械臂能否顺利完成采样任务,是衡量机械臂操作性能的重要指标,提高机械臂绝对定位精度对于确保采样任务完成至关重要[3⁃4]。
由于受到加工装配误差、关节背隙、编码器误差等因素影响,机械臂实际运动参数与名义运动参数之间存在误差,导致机械臂末端绝对定位精度下降[5]。此外,对于表取机械臂而言,两杆件为细长杆,跨度较大,杆件上的微小变形映射到机械臂末端会产生较大的末端位置误差,机械臂自重、负载及外力等引起的弹性变形是导致机械臂末端位置误差的主要原因。
分析弹性变形对机械臂末端位置误差影响,需要建立弹性变形量对于末端位置误差映射关系。针对该问题,国内外学者进行了大量研究。Khalil等基于逆向动力学模型对关节、杆件进行受力分析,建立坐标系间弹性传递矩阵,并推导构造几何参数与弹性参数雅可比矩阵[6];Meggiolaro 等以多项式近似的方法建立了弹性误差模型[7];Zhou 等通过分析关节附加力矩与末端负载映射关系建立有关关节变形的弹性误差模型[8];刘志等对机械臂杆件弯曲变形进行分析并提出一种考虑结构变形的运动学补偿模型[9];伍小凯通过建立几何误差与弹性误差综合运动学误差模型对机器人进行了运动学辨识[10];陈宵燕采用线性扭簧理论构建机械臂柔度误差模型,并基于此建立了机器人刚柔耦合模型[11]。
调研结果表明:现阶段弹性建模方法并未综合考虑静外力/力矩对机械臂杆件、关节产生的拉伸、弯曲、扭转变形的影响,造成弹性变形量与机械臂末端误差间映射关系表征不准确,从而导致后续几何参数标定精度不高。针对表取机械臂多种弹性变形耦合引起的末端绝对定位精度问题,本文建立了受弹性变形影响的机械臂弹性误差模型;在此基础上,结合几何误差模型建立机械臂综合误差模型,并通过几何参数标定的方法对末端绝对定位误差进行补偿;通过实验验证了文中提出精度补偿方法的有效性。
1 机械臂运动学建模
有效的运动学模型必须满足完备性、比例性和连续性的要求[12]。机械臂运动学建模常常使用Denavit⁃Hartenberg (DH)法,表取机械臂由一 个偏航关节和3 个俯仰关节组成[13⁃14]。由于3 个俯仰关节均为平行关节,而平行关节坐标系之间运动学参数对两轴之间的夹角误差非常敏感[15],当两平行关节轴间存在微小夹角时,会引起运动学参数突变,不满足有效的运动学模型要求。因此,本文采用改进的DH(Modified DH, MDH)方法建立运动学模型[16],MDH 方 法 采 用αi、ai、θi、di、βi这5 个 参 数 描述杆件间的关系。其中:αi称为杆件i 扭角,即关节i 和关节i+1 轴线的夹角;ai为杆件i 长度,即关节i 和关节i+1 轴线公垂线长度;θi为关节i 的转角,即杆件i 和杆件i+1 轴线的夹角;di为关节i 的偏置,即杆件i 和杆件i+1 轴线公垂线偏置;βi与αi类似,同样用于描述两关节间轴线夹角。
“嫦娥5”表取机械臂MDH 坐标系及MDH 参数分别如图1 及表1 所示。
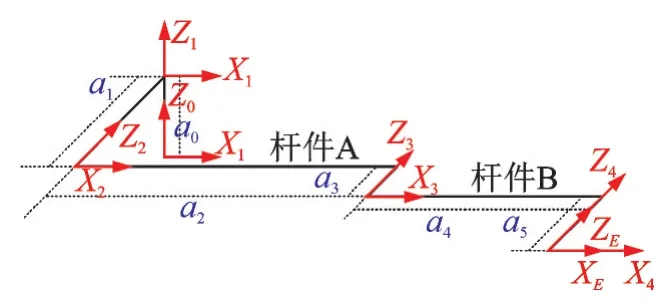
图1 表取机械臂MDH 坐标系Fig.1 MDH coordinate systems of the manipulator

表1 表取机械臂MDH 参数Table 1 MDH parameters of lunar sampling manipulator
机械臂杆件坐标系间变换可以表示为

式中:i=1,2,3,4;Trot(X,αi)表示绕X 轴旋转αi变换矩阵;Ttrans(X,ai)表示沿X 轴平移ai变换矩阵;Trot(Z,θi)表示绕Z 轴旋转θi变换矩阵;Ttrans(Z,di)表示沿Z 轴平移di变换矩阵;Trot(Y,βi)表示绕Y轴旋转βi变换矩阵。
从惯性坐标系到末端坐标系的转换关系为
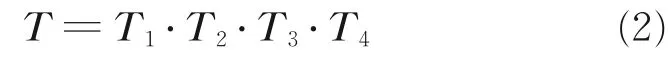
2 机械臂弹性误差建模
分析杆件、关节因静外力导致的弹性变形量,基于此推导杆件弹性模型与关节弹性模型,综合两者建立机械臂综合弹性误差模型。表取机械臂的实际工作环境为月球重力环境,为保证地面模拟实验精度满足机械臂实际工作精度要求,需要模拟月球的重力环境,往往采用施加静态吊点力的方式来补偿地球重力环境,在进行受力分析时需要考虑吊点力对关节、杆件弹性变形的影响。
2.1 杆件弹性变形分析
杆件A 与杆件B 跨度较大,在机械臂自身重力、机械臂上携带的设备等载荷的重力、操作物的重力等共同作用下发生弯曲、拉伸、扭转变形。
2.1.1 杆件B 末端弹性变形误差量
将杆件B 视为首端固定、末端自由的悬臂梁进行受力分析[17],杆件B 主要受力为自身重力G4、远摄像机重力Gc、吊点力F1;所受力矩为远摄像机重力产生力矩Mc、吊点力产生力矩MF1。
如图2 所示,将杆件4 的重力和机械臂末端负载简化到杆件B 末端(关节4 轴线与杆件B 轴线的交点),得主矢G4和主矩M4,主矩M4分解为M4P与M4V,则有
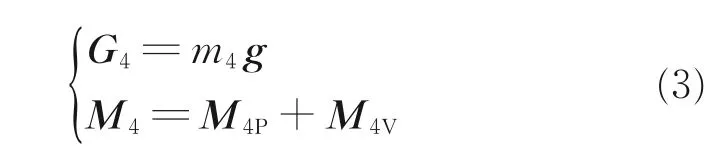
式中:M4P数值为M4P=m4g(a5-r4z);M4V数值为M4V=m4gr4xcosφ4;m4为 杆 件4 质 量;g 为 重 力 加速度;r4x、r4z分别为杆件4 质心在∑E系下的位置矢量沿XE和ZE轴分量。
受力分析如图3 所示。杆件B 与水平方向的夹角φ3=θ2+θ3,将G4可分解为G4τ和G4n,G4τ使杆件拉伸,G4n使杆件向+y 方向弯曲,M4P可分解为M4Pτ和M4Pn,M4Pτ使 杆 件 沿+x 方 向 扭 转,M4Pn使杆件向+z 方向弯曲,M4V使杆件向+y 方向弯曲。杆件自身的重力GB形成均匀载荷qB=mBg/lB(mB为杆件B 质量,lB为杆件B 长度)分解为qBτ和qBn,qBτ使 杆 件 拉 伸,qBn使 杆 件 沿+y 方 向弯曲。远摄像机的重力简化到杆件轴线上,得主矢Gc=mcg 和主矩Mc=-mcgrcz(mc为远摄像机质量,rcz为远摄像机质心在∑E系下的位置矢量沿ZE轴 分 量 的 模),Gc、Mc引 起 的 杆 件 变 形同G4、M4。

图2 杆件4 重力向杆件3 末端等效示意图Fig.2 Equivalent diagram of gravity of link 4 toward the end of link 3
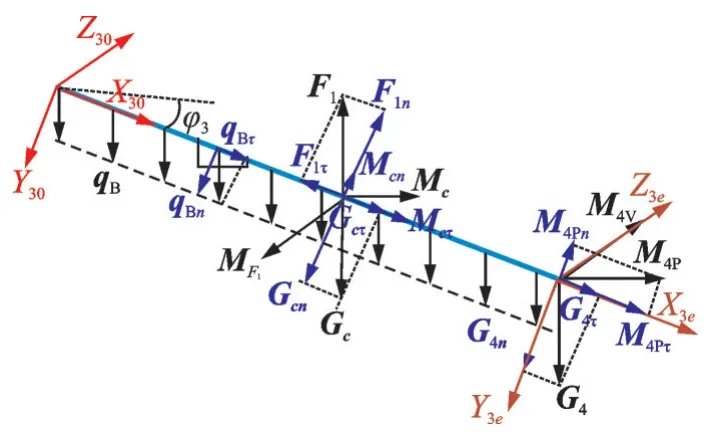
图3 杆件B 受力分析Fig.3 Schematic drawing of force analysis of link B
吊点在杆件B 上加一个竖直向上的力F1和力矩MF1,其中:MF1=FdFsinφ3,dF为吊点力作用点到杆件B 轴线的垂直距离。F1可分解为F1τ和F1n,F1τ使 杆 件 拉 伸,F1n使 杆 件 向-y 方 向 弯 曲;MF1使杆件向-y 方向弯曲。
杆件B 的变形示意图如图4 所示,杆件B 的末端由B1点移动到B2点,则∑3e系的微分移动和转动DBe为

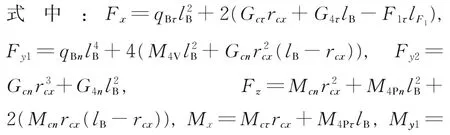

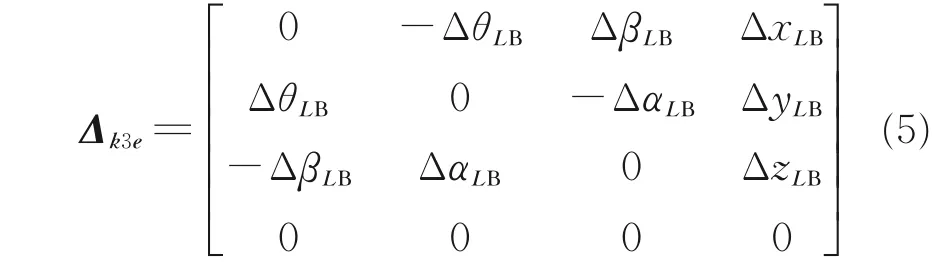
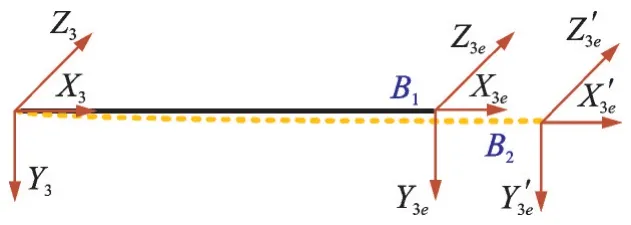
图4 杆件B 的变形示意图Fig.4 Schematic drawing of deformation of link B
2.1.2 杆件A 末端弹性变形误差量
杆件A 主要受力为杆件3、杆件4 重力G34以及自身重力均匀载荷qA,对杆件A 按照杆件B 的分析思路进行处理,得到杆件A 受力分析图如图5 所示。杆件A 末端坐标系∑2e微分移动和转动DAe为

式中:qAτ、qAn为qA分力,分别使杆件拉伸和沿+y方向弯曲;G34τ、G34n为G34分力,使杆件拉伸变形和沿+y 方向弯曲;M34P、M34V为杆件3、杆件4 重力向杆件A 末端转换时的等效力矩分力矩,M34Pτ、M34Pn则 为M34P分 力 矩,M34Pτ使 杆 件 沿+x 方 向 扭 转,M34Pn使 杆 件 向+z 方 向 弯 曲,M34V使 杆 件 向+y 方向 弯 曲;EAA为 杆 件A 抗 拉 刚 度,EIA为 杆 件A 弯曲 刚 度,GIpA为 杆 件A 扭 转 刚 度,lA为 杆 件A 长度。微分变换为
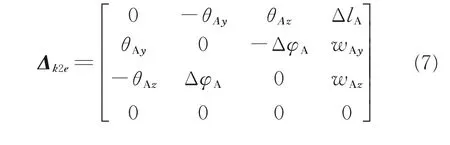
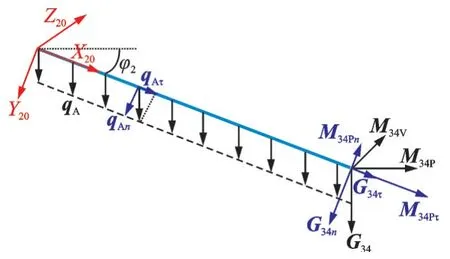
图5 杆件A 受力分析图Fig.5 Schematic drawing of force analysis of link A
2.2 关节弹性变形分析
关节弹性变形主要为绕关节转动方向的扭转变形,拉伸变形与弯曲变形可忽略不计。关节受力主要为末端负载重力、吊点力、其余关节以及杆件重力。
2.2.1 关节4 坐标系弹性变形误差量
如图6 所示,关节4 主要受到杆件4 重力以及末端负载影响。
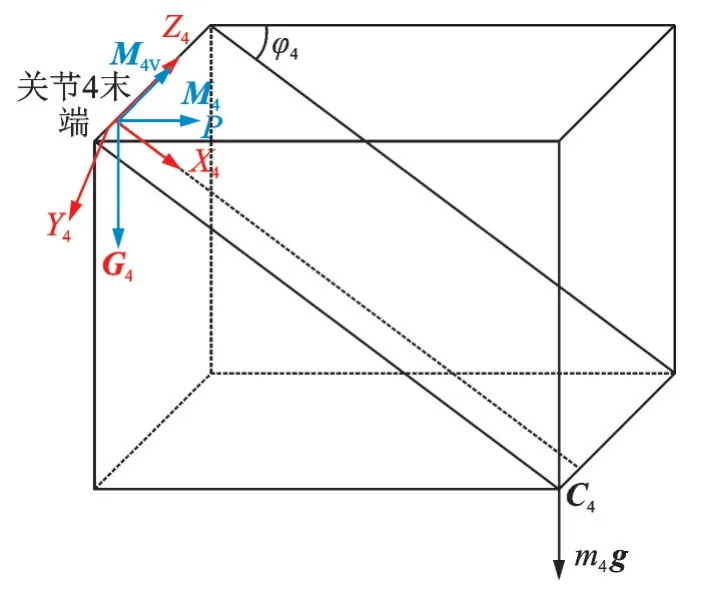
图6 杆件4 重力向关节4 简化示意图Fig.6 Equivalent diagram of gravity of link 4 toward joint 4
将杆件4 的重力和机械臂末端负载简化到关节4 末端(关节4 轴线与杆件4 轴线的交点),得主矢G4=m4g 和 主 矩M4=M4P+M4V。 式 中:M4V=m4gr4xcosφ4,φ4=θ2+θ3+θ4,M4V使关节4 沿+z 方 向 扭 转;m4为 杆 件4 质 量,r4x、r4z分 别 为杆件4 质心在∑4系下的位置矢量沿X4和Z4轴分量。
关节4 受力分析图如图7 所示。则∑4系相对于∑3e系的微分移动和转动为
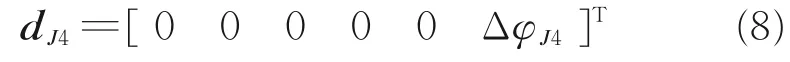
2.2.2 其余关节坐标系弹性变形误差量
关节3 在杆件B、关节4、杆件4 的重力和机械臂末端负载合力G34以及吊点力F1作用下产生扭转变形,其受力分析如图8 所示。∑3系相对于∑2e系的微分移动和转动为

图7 关节4 受力分析图Fig.7 Schematic drawing of force analysis of joint 4

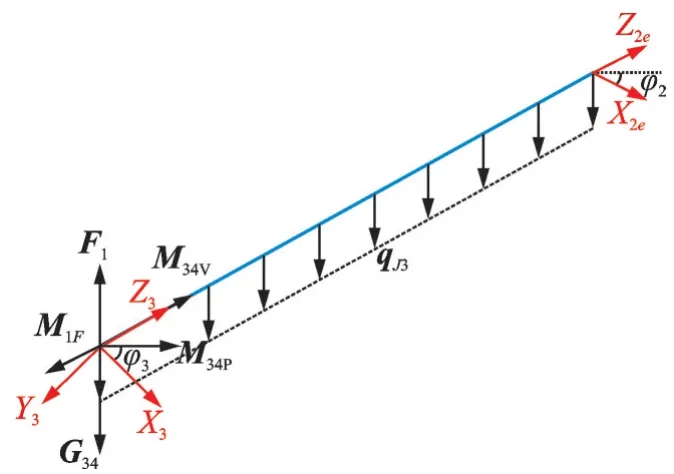
图8 关节3 受力分析图Fig.8 Schematic drawing of force analysis of joint 3
关节2 扭转变形为杆件A、关节3、杆件B、关节4、杆件4 的重力和机械臂末端负载合力G234以及吊点力共同作用的结果,其受力分析图如图9所示。
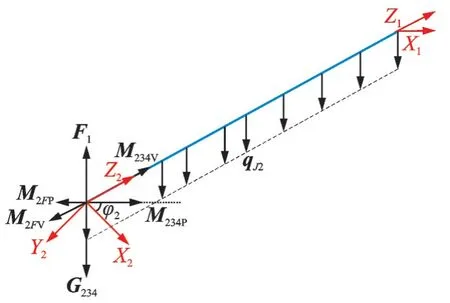
图9 关节2 受力分析图Fig.9 Schematic drawing of force analysis of joint 2
∑2系相对于∑1系的微分移动和转动为

G234、吊点力向关节2 末端(关节2 轴线与杆件A 轴线的交点)转换等效力矩分力矩,GIpJ2为关节2 扭转刚度。
关节1 受力分析图如图10 所示。

图10 关节1 受力分析图Fig.10 Schematic drawing of force analysis of joint 1
由受力分析图可知,关节1 无扭转变形,则∑1相对于∑0的微分移动和转动为

2.3 弹性误差建模
机械臂弹性变形包括关节弹性变形与杆件弹性变形两部分,关节、杆件弹性变形将导致末端坐标系发生偏移,与运动学参数造成的末端位置误差发生耦合,导致几何参数无法准确辨识出来。去除弹性误差影响,对于提高几何参数标定结果精度至关重要。
2.3.1 关节弹性模型
设T 和T′分别为惯性系到末端坐标系的名义变换矩阵和实际变换矩阵,则

关节弹性变形后机械臂运动学模型为
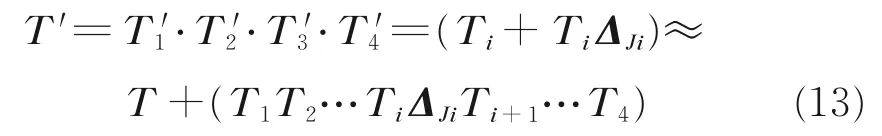
由式(12)和式(13)可得关节弹性变形导致的末端变换矩阵微分dT 为

进一步推导可得到关节弹性变形导致的末端位置误差Df_J为
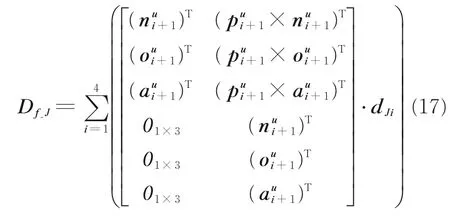
定义关节i 弹性变形引起的位置误差与末端位置误差之间的传递矩阵为
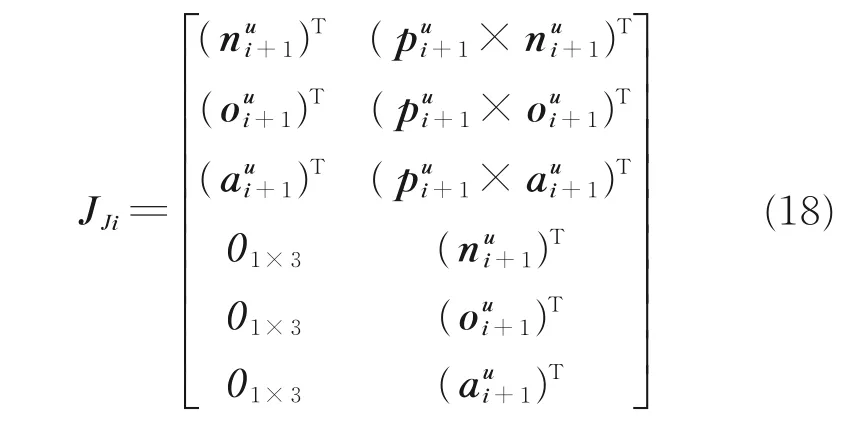
则式(17)可以写为

式中:Jf_J=[JJ1JJ2JJ3JJ4]表示关节弹性误差与末端位置误差之间的误差传递矩阵,df_J=[dJ1dJ2dJ3dJ4]T为关节弹性误差向量矩阵,各个误差向量如式(8)至式(11)所示。
2.3.2 杆件弹性模型
由式(4)和式(6)可以得到∑2e系和∑3e系分别有位置误差DAe、DBe。考虑杆件变形的机械臂坐标系如图11 所示。对于∑2系与∑3系的变换矩阵T3,设∑2系与∑2e系的变换矩阵为T31,∑2e系与∑3系的变换矩阵为T32;对于∑3系与∑4系的变换矩阵T4,设∑3系与∑3e系的变换矩阵为T41,∑3e系与∑4系的变化矩阵为T42。则


图11 考虑杆件变形的机械臂坐标系Fig.11 Coordinate systems considering deformation of links
由于杆件变形,使得矩阵T31和T41分别有微分变换Δk2e和Δk3e,即矩阵T31和T41的实际值为
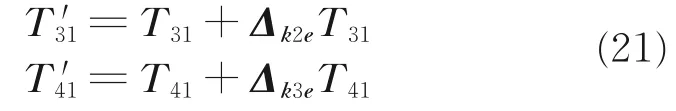
杆件变形后机械臂末端坐标系相对于惯性系的变换矩阵为
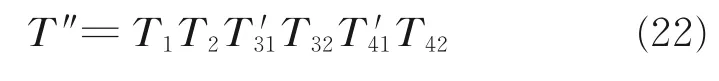
忽略高阶无穷小,结合式(12)可得
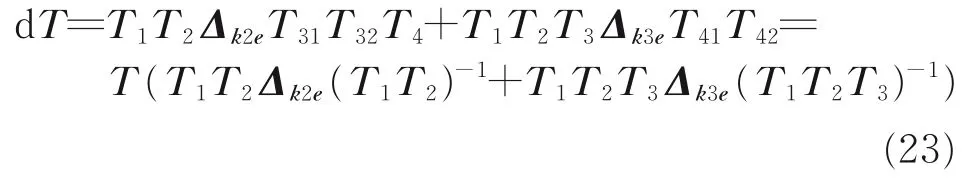
定义dT =TΔL,则

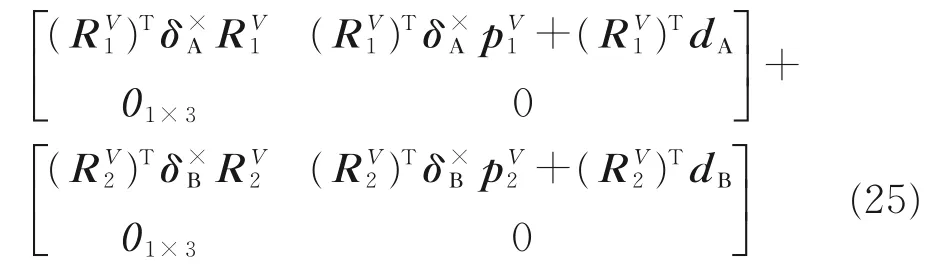
可得由杆件变形产生的末端位置误差Df_L在惯性系下的表示为

2.3.3 综合弹性误差模型
定义Jf=[Jf_LJf_J],表示弹性误差与末端位置误差之间的误差传递矩阵,df=[df_Ldf_J]T为弹性误差向量矩阵,则综合杆件弹性误差模型与关节弹性误差模型可得到弹性变形引起的末端位置误差向量为
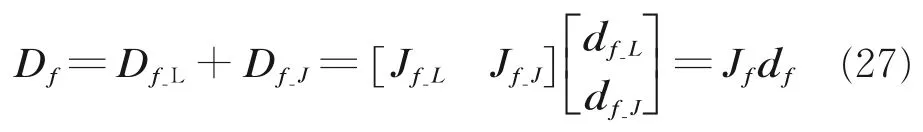
3 机械臂末端综合精度补偿
机械臂末端位置误差包括由几何参数误差引起的位置误差和弹性变形引起的位置误差两部分。上文已完成弹性误差建模工作,下面主要对几何参数误差建模,然后对机械臂末端位置误差进行耦合性分析,分离由关节、杆件变形导致的末端位置误差,最终对几何参数进行标定。
3.1 几何参数误差建模
对于杆件坐标系,设Ti和Ti′ 分别为{i+1}系相对于{i}系的名义变换矩阵和实际变换矩阵,对变换矩阵微分进行一阶近似,可得

由式(28)可得相邻杆件坐标系相对于惯性系的位置误差矩阵为
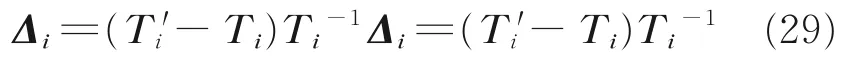
对变换矩阵微分进行一阶近似,可由式(30)计算[18]
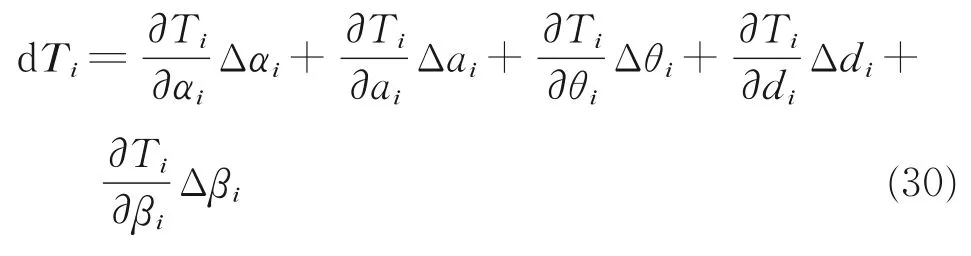
计算得
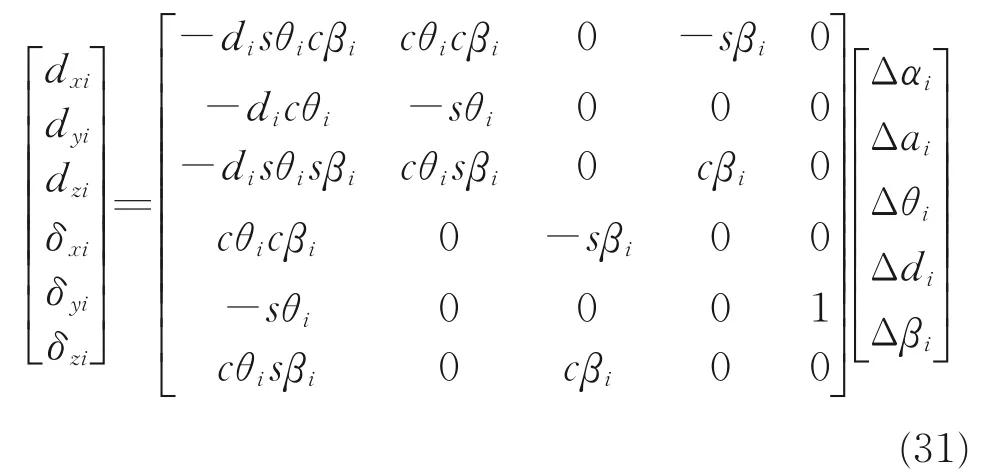
设T 和T′分别为惯性系到末端坐标系的名义变换矩阵和实际变换矩阵,则
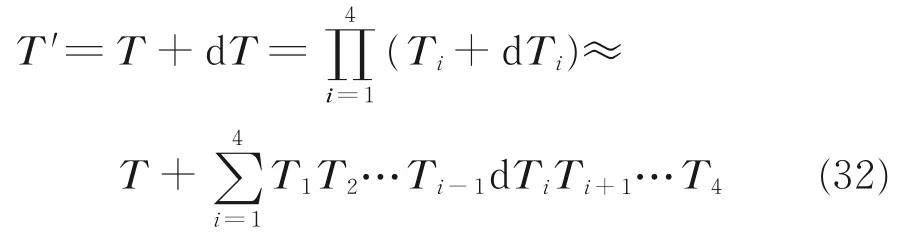
由式(28)和式(32)可得

令Ui=TiTi+1…Tn(i=1,2,3,4),Un+1=I4,式(33)可化为

则Δ 可写为
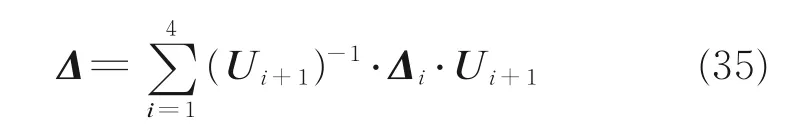
定义Dg为由几何参数误差引起的末端位置误差向量

由式(35)和式(36)可推导出

令Jgi表示几何参数误差与末端位置误差之间的误差传递矩阵; ei=[ ΔαiΔaiΔθiΔdiΔβi]T(i=1,2,3,4)表示几何参数误差。式(37)可写为

3.2 模型参数耦合性分析
综合几何误差模型与弹性误差模型,可得到机械臂末端位置误差向量为
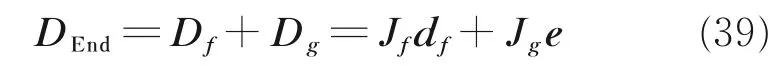
式中:DEnd=PEmeas-PEnom,PEmeas为末端位置测量值,PEnom为末端位置理论值。
由式(39)表示的机械臂末端位置误差向量中,末端位置理论值PEnom、由弹性误差引起的末端位置误差Df、由几何参数误差引起的末端位置误差Dg、弹性误差与末端位置误差之间的传递矩阵Jf、几何参数误差与末端位置误差之间的传递矩阵Jg,均为几何参数的函数;此外,由于关节和杆件所受力矩阵FLi和FJi均为动力学参数的函数,因此由弹性变形引起的末端位置误差向量df为几何参数和弹性参数的函数。
以E 表示全部几何参数,S 表示全部弹性参数,则有
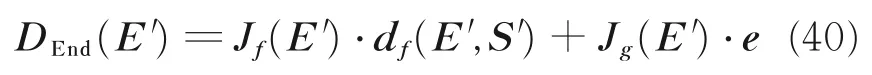
式中:E′=E+e,S′=S+Δs。式(40)中几何参数误差与弹性参数误差存在耦合,忽略高阶无穷小量,可将式(40)简化为
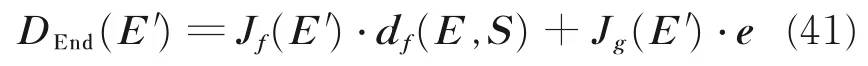
3.3 综合精度补偿
经过上述分析可知,末端位置误差是几何参数和弹性参数共同作用的结果,几何参数的标定会受弹性参数误差的影响,因此需先对弹性参数进行标定,然后再对几何参数误差进行标定,精度补偿流程如图12 所示。
由于几何参数误差与末端位置误差之间的关系是线性的,因此采用最小二乘法进行标定。对于n 自由度串联机器人,利用MDH 建立的运动学模型中含有5n 个几何参数,取m 组末端位置构建超定方程组,如式(42)所示。为保证顺利求解,m 应取大于5n/6 的整数。

本文只关注机械臂末端绝对定位误差,即式(42)中Dg1…Dgm以及Jg1…Jgm均只有前三行有效,后三行中对应的末端姿态误差均为零。因此,为了顺利求解全部的几何参数,要求m 应取大于5n/3的整数。
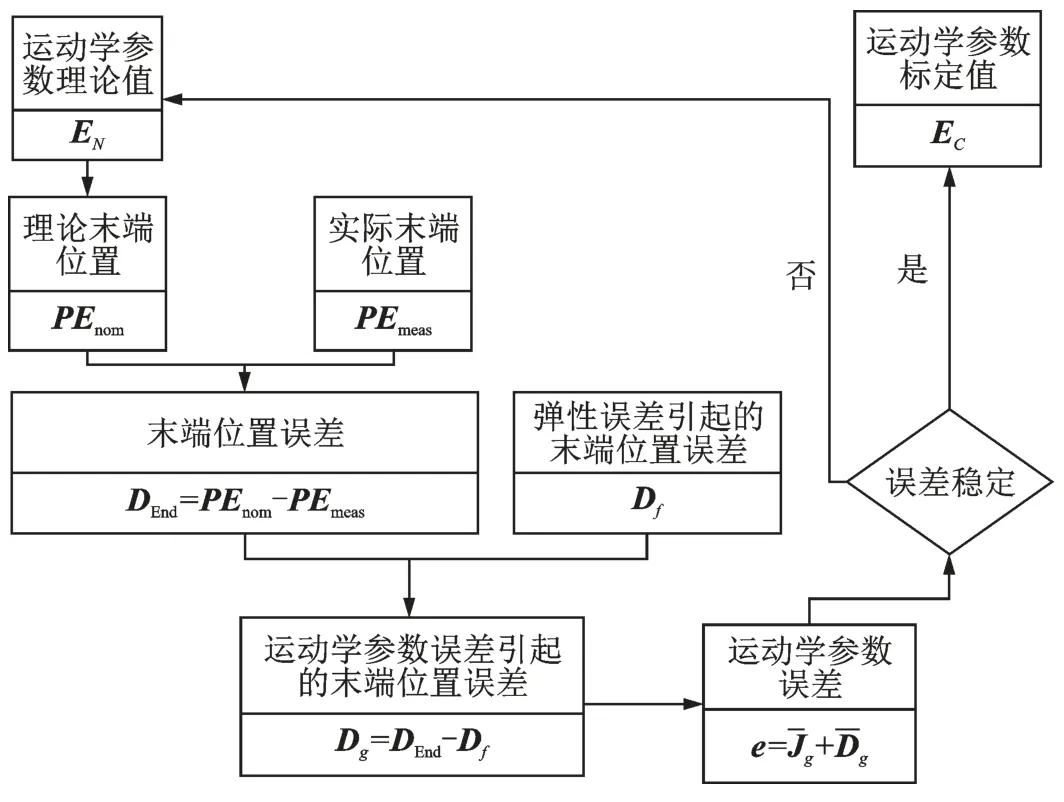
图12 精度补偿算法流程图Fig.12 Flowchart of algorithm for accuracy compensation

利用最小二乘法求解式(43),可得

为保证得到的几何参数具有足够的精度,需要利用最小二乘法进行有限次迭代,以Ej=[αjajθjdj]T( j=1,…,N )表示第j 次标定过程输入的几何参数,则有
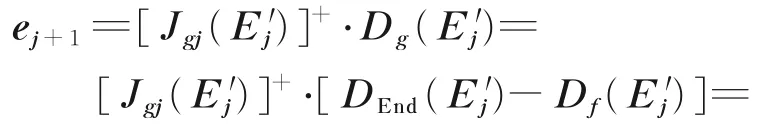
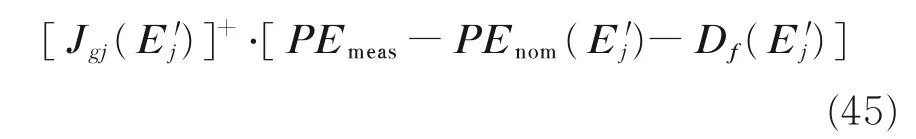
式中:当j=1 时(即第一次标定过程),取e1=0,E1为初始几何参数,E′j=Ej+ej。式(45)的收敛条件为ej+1=0。
4 实验与结果分析
为了对本文所提出的考虑弹性变形的精度补偿方法的正确性和有效性进行验证,选取28 组关键构型,利用激光跟踪仪测得28 组构型绝对末端位置,将测得的末端位置作为输入,利用本文提出的精度补偿方法求解坐标系运动学参数误差,进而得到机械臂坐标系运动学参数。如表2 所示为补偿前后机械臂MDH 参数值以及误差值。

表2 表取机械臂补偿前后的MDH 参数Table 2 MDH parameters before and after compensation
对标定结果进行验证,选取50 组验证构型,对比精度补偿前后机械臂末端位置误差。同时,忽略弹性变形对机械臂末端位置误差的影响,仅对运动学参数进行辨识,并基于辨识获得的坐标系运动学参数计算50 组验证构型末端位置误差。补偿前、考虑弹性变形进行补偿、忽略弹性变形仅进行运动学参数辨识3 种情况末端位置误差沿X、Y、Z 坐标轴的分量以及三轴合成误差如图13 所示。
对实验数据进行处理,可以得到补偿前后末端位置误差在各个坐标轴上的最大值、最小值和平均值如表3 所示。
分析表3 中数据可以看出,补偿后末端位置误差沿各个坐标轴的平均值比标定前有明显下降,误差沿X、Y、Z 三轴分量的平均值分别下降88.90%、92.81%、93.13%,三轴合成的位置误差平均值下降92.16%。补偿后末端位置误差沿各个坐标轴的最大值比标定前分别下降87.67%、84.87%、89.01%,三轴合成的位置误差最大值下降88.63%。而且,综合精度补偿后末端位置误差较几何标定末端位置误差更小、效果更优。通过分析可知,利用本文提出考虑弹性变形的精度补偿方法得到的机械臂运动学参数精度较高,能够大幅提高表取机械臂末端绝对定位精度。

图13 精度补偿前后末端位置误差Fig.13 Positioning error before and after compensation

表3 精度补偿前后末端位置误差对比Table 3 Comparison of positioning error in different sit⁃uations
5 结 论
针对大跨度、低刚度的表取机械臂存在的末端绝对定位精度问题,本文首先对机械臂关节、杆件进行了受力分析和形变分析,并推导了机械臂弹性误差和末端位置误差间的映射关系,从而建立了机械臂弹性误差模型;然后,基于机械臂的MDH 运动学模型建立了机械臂几何误差模型,表征机械臂运动学参数误差和末端位置误差间的映射关系;进而,建立弹性机械臂综合误差模型并且设计了可适用于表取机械臂的精度补偿方法,并进行仿真验证。结果表明,该方法能够获得准确的机械臂运动学参数,大幅提高机械臂末端绝对定位精度。
