纳米氧化镧和蛇纹石改性PTFE复合材料淡水环境摩擦学性能预测*

闫艳红 吴子健 卢 欢 王腾彬 郝彩哲 贾志宁

(1. 燕山大学机械工程学院，河北省轻质结构设计与制备工艺技术创新中心 河北秦皇岛 066004； 2.承德石油高等专科学校 河北承德 067000)

随着科学技术的进步， 淡水环境下机械摩擦副摩擦磨损问题已逐渐成为研究热点。传统的摩擦副材料多以金属为主，其自身易生锈、腐蚀等，造成了巨大的经济损失和能源浪费[1-3]。因此，开发淡水环境下性能优良、经济环保的新型材料尤为重要[4-6]。

近年来，新型水润滑材料不断涌现，如改性橡胶、新型尼龙、改性聚乙烯等，这些聚合物及其复合材料摩擦副与金属摩擦副相比，具有高强度、低磨损、耐腐蚀等优点，可应用于更复杂极端的工作环境[7-9]，但仍存在摩擦因数偏高的缺点[10-12]。

聚四氟乙烯(PTFE)高分子材料具有摩擦因数低、分子结构稳定等优点，被广泛应用于工业生产、化工机械当中。但纯PTFE存在硬度低、耐磨性能差两大缺点，因此采用纳米颗粒改性PTFE成为研究热点[13-14]。蛇纹石(serpentine)具有磨损自修复功能，作为添加剂可提高PTFE复合材料硬度及降低其磨损率。JIA和YANG[15-16]证明了PTFE中添加nano-serpentine后耐磨性能得到极大提高;闫艳红等[17]将亚微米级蛇纹石融入润滑油品中改善了油品性能。研究表明，nano-La2O3作为添加剂不仅具有减摩耐磨作用[18-19]，而且对超细serpentine在加热情况下的相变过程起到了催化作用[20]。

本文作者以PTFE为基体，以nano-La2O3、nano-serpentine为添加剂制备复合材料(nano-La2O3/nano-serpentine/PTFE)，采用均匀设计与多元回归相结合的方法，预测PTFE基复合材料的最优配比，通过实验和磨损机制分析对预测结果进行分析论证，为高分子材料的性能预测和应用提供一定的理论和实验依据。

1 试验部分

1.1 试验材料

PTFE粉末：牌号m111，平均粒度为500 μm，东莞兴旺塑料原料有限公司生产；硅烷偶联剂KH-550：牌号KH-550，南京创世化工助剂有限公司生产；nano-La2O3粉末：牌号La2O3，平均粒度50 nm，上海吉至生化科技有限公司生产；nano-Serpentine粉末：自制，使用美国SPEX SamplePrep公司生产的8000D-230型球磨机制备。

1.2 复合材料制备

试验设计方法选择2因素8水平的均匀设计法，PTFE基复合材料不同水平配比如表1所示。

表1 Nano-La2O3/nano-serpentine/PTFE 复合材料不同水平配比 单位:%Table 1 Ratio of nano-La2O3/nano-serpentine/PTFE composite materials of different levels Unit:%

PTFE基复合材料的制备采用类似“粉末冶金”方法，以PTFE模压粉和纳米级添加剂粉末作为原料，制备复合材料。具体制备过程包括添加剂表面改性、材料混合、冷压成型和真空烧结[21-23]。

文中采用无水乙醇作为溶剂，硅烷偶联剂KH-550作为改性剂对nano-La2O3和nano-serpentine进行表面改性，提高纳米添加剂的分散性，降低团聚程度。采用超声震荡与高频搅拌相结合的方法，使基体与添加剂混合均匀。混合过程为：在烧杯中倒入100 mL无水乙醇，加入0.1 mL硅烷偶联剂，使用超声震荡仪和搅拌器对其进行超声震荡、搅拌，持续15 min；待偶联剂与无水乙醇充分混合后，按照复合材料不同水平配比将指定质量的干燥nano-serpentine粉体缓慢加入其中，持续超声震荡、搅拌10 min；随后按照配比缓慢加入指定质量的干燥nano-La2O3粉体，持续超声震荡、搅拌10 min；最后按照配比缓慢加入指定质量的PTFE模压粉，持续震荡、搅拌30 min，得到基体与添加剂充分混合的悬浊液；将悬浊液放入干燥箱中，在100 ℃环境下烘干至得到干燥的混合粉体。

冷压成型工艺中加载压力为40 MPa，加压时间为1 min，保压时间为30 min。

真空烧结在锦州航星真空设备有限公司生产的ZRY-120型热模压机上进行，其加热工艺曲线如图1所示。

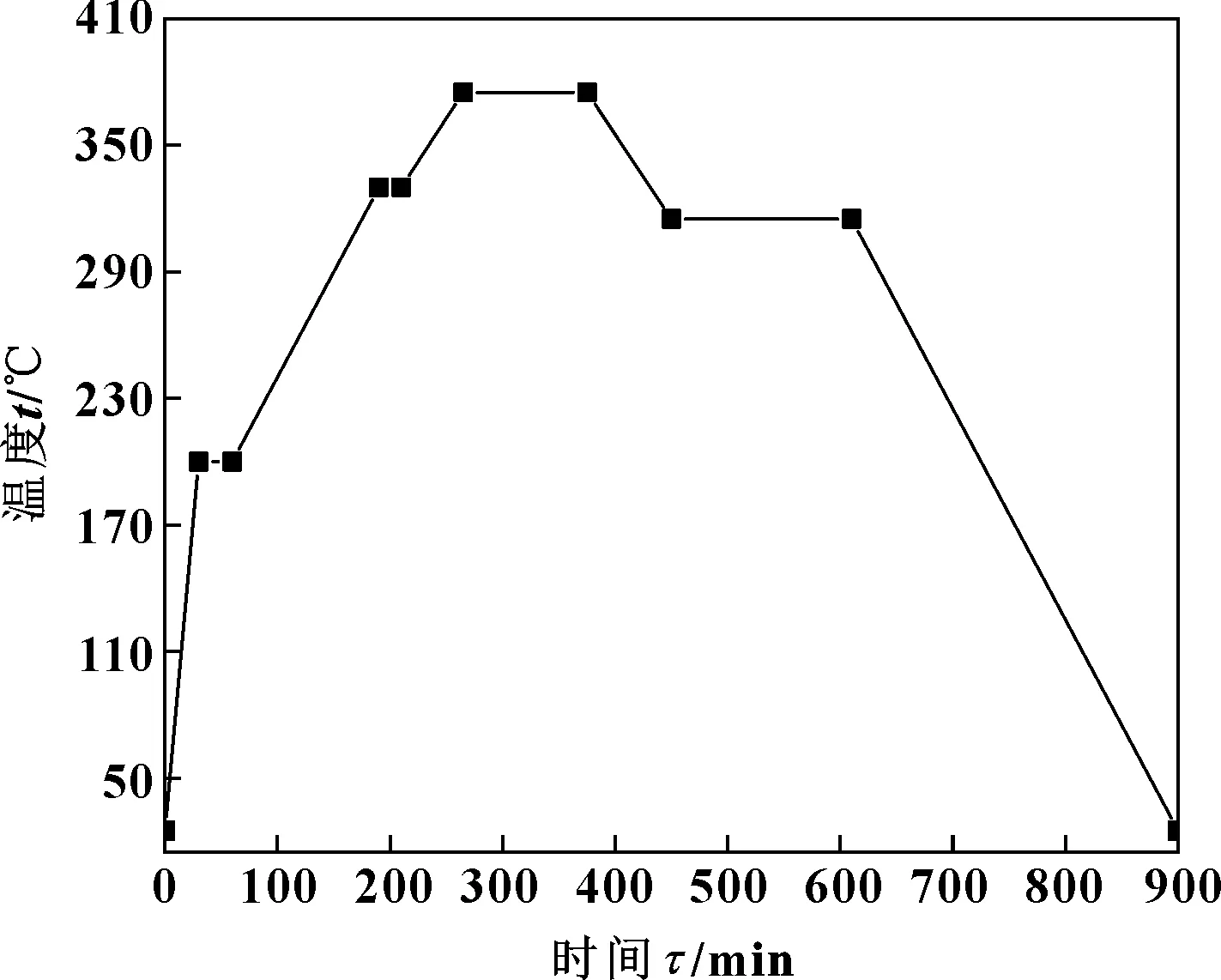
图1 复合材料烧结工艺曲线Fig 1 Composite material sintering process curve

1.3 摩擦学性能测试

摩擦学实验在济南思达测试技术有限公司生产的MMU-5G摩擦磨损试验机上进行，选取316L不锈钢为摩擦实验上试件，PTFE基复合材料为下试件，上、下试件组成摩擦副。其运动形式为滑动，接触压力为4 MPa。组合前后如图2所示。

图2 摩擦副组合前后示意Fig 2 Schematic of the friction pair before and after combination

自制淡水环境模拟装置，模拟实验所需的流动淡水环境，水环境模拟装置如图3所示，图中1、2、3、4为进水部分，5为摩擦实验进行部分，6、7、8为回收水部分，9为摩擦磨损试验机。

图3 水环境模拟装置Fig 3 Water environment simulation device

摩擦学试验压力为128 N，转速为200 r/min，工作时间为60 min。下试件每个水平为1组，每组做4次试验，取其中3次稳定实验数据的平均值作为该水平最终实验结果。

作为评价摩擦学性能的重要指标之一，磨损率表征了材料的耐磨性。在测量磨损率时，首先使用德国GFMesstechnik GmbH公司生产的MikroCAD Lite表面形貌测量仪测量磨痕参数，再利用体积公式计算出磨损体积，最后通过磨损率计算公式计算出磨损率，磨损体积与磨损率计算公式如下：

V=SH

(1)

K=V/(FL)

(2)

式中:V为磨损体积;S为磨损截面积:H为磨痕长度;K为磨损率;F为施加载荷;L为滑动距离。

1.4 磨损表面形貌观测

使用日本日立公司生产的Hitachi S3400N场发射扫描电镜观察复合材料磨损表面微观形貌。

2 结果与讨论

2.1 最优摩擦因数

2.1.1 直观分析

均匀设计法具有均匀分散的特性，各个水平每种因素大小的选取相互之间无干扰，因此借助整体实验结果分析单一因素对实验结果的影响具有一定参考价值。图4、图5示出了摩擦因数大小随添加剂质量分数的变化。

图4 摩擦因数随nano-La2O3质量分数的变化Fig 4 Variation of friction coefficient with nano-La2O3 mass fraction

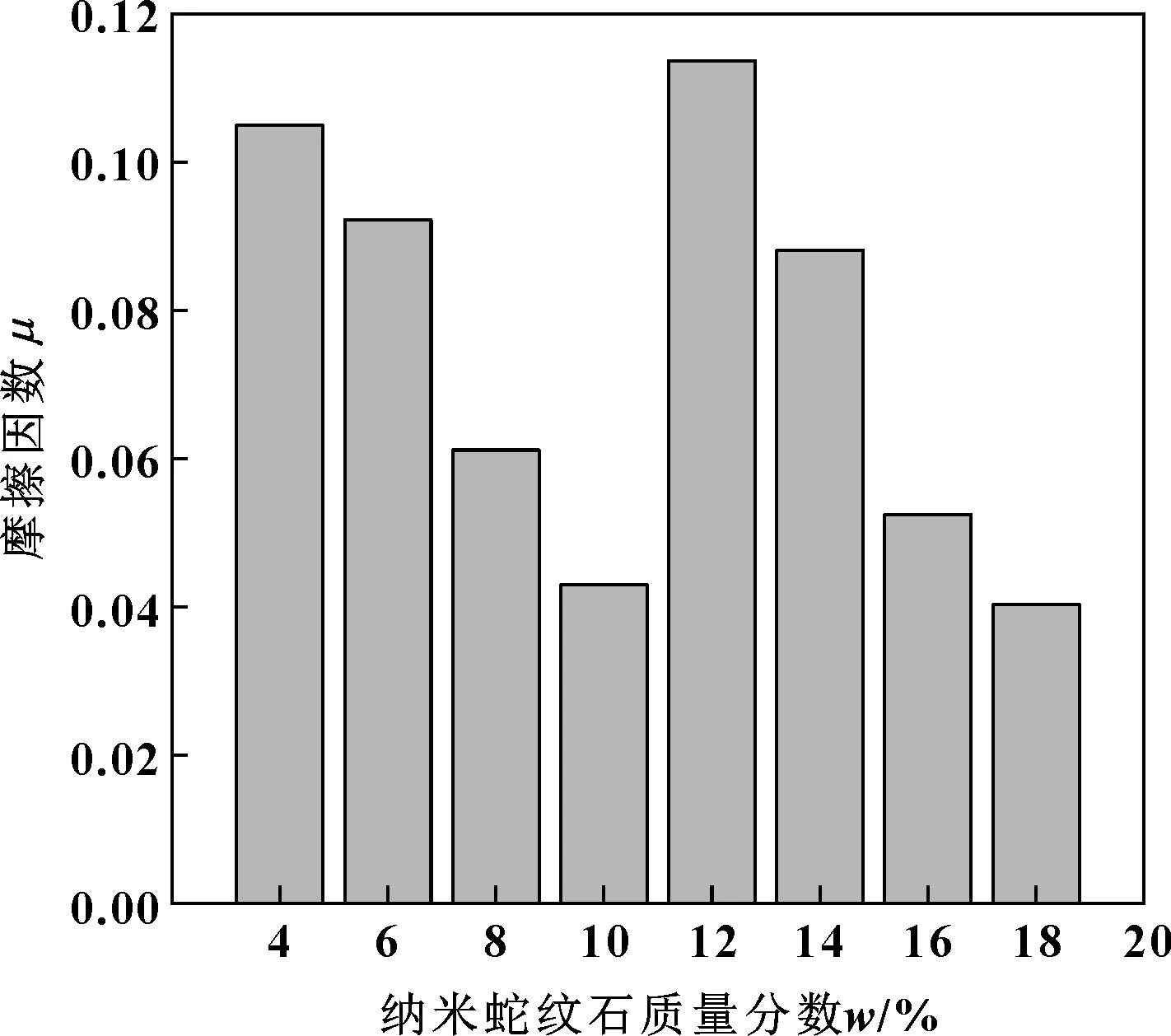
图5 摩擦因数随nano-serpentine质量分数的变化Fig 5 Variation of friction coefficient with nano-serpentine mass fraction

由图4可知，随着复合材料中nano-La2O3质量分数不断提高，复合材料摩擦因数基本呈增加趋势。当nano-La2O3质量分数为5%时，复合材料摩擦因数最低，仅为0.040 3，当质量分数超过9%时，摩擦因数显著提高。分析认为，nano-La2O3质量分数低于9%的nano-La2O3复合材料摩擦因数较低，质量分数过高会导致复合材料摩擦因数增加。

由图5可知，试件的摩擦因数大小和nano-serpentine质量分数之间并非简单的线性关系，随着nano-serpentine质量分数提高，摩擦因数存在2个极小值点且大小十分接近。在2个极小值点，nano-serpentine的质量分数分别为10%和18%。分析认为：摩擦因数最优时蛇纹石质量分数应该在这2个点附近。为排除nano-La2O3质量分数过高可能造成的影响，删除第一列和第五列(如表1所示，此两列nano-La2O3质量分数最高，分别为15%和17%)，发现摩擦因数走势与分析结果不变，由此可以排除nano-La2O3质量分数随机性对分析结果的影响。

综合图4和图5，当nano-La2O3质量分数为3%～9%，nano-serpentine质量分数处于2个极小值点10%和18%附近时，复合材料摩擦因数最小。

2.1.2 多元回归分析

使用多元回归方法对实验结果进行分析，首先使用Origin软件对摩擦因数随nano-La2O3质量分数变化函数关系进行曲线拟合，拟合出函数类型为多项式函数，函数关系式为

(3)

式中:X1为nano-La2O3质量分数；φ1为nano-La2O3影响下的摩擦因数。

方差分析如表2所示。表中X1与φ1的相关系数大于0.95(相关系数为回归平方和与整体平方和之间比值)，回归效果显著，显著性大小为0.002 8，小于0.05，通过了F假设检验，可认为摩擦因数随nano-La2O3质量分数变化曲线拟合成功[24]。

表2 nano-La2O3质量分数与摩擦因数关系方差分析Table 2 Variance analysis of relationship between nano-La2O3 mass fraction and friction coefficient

然后使用Origin软件对摩擦因数随nano-serpentine质量分数变化的函数关系进行曲线拟合，拟合出函数类型为正弦函数，函数关系式为

φ2=0.074 52+0.035 3sin[π(X2-0.027 73)/

0.040 83]

(4)

式中:X2为nano-serpentine质量分数；φ2为nano-serpentine影响下的摩擦因数。

方差分析如表3所示。表中X2与φ2的相关系数大于0.95，回归效果显著，显著性大小为0.000 554，小于0.05，通过了F假设检验，可认为摩擦因数随nano-serpentine质量分数变化曲线拟合成功。

表3 nano-serpentine质量分数与摩擦因数关系方差分析Table 3 Analysis of variance of nano-serpentine mass fraction and friction coefficient

使用SPSS软件，以摩擦因数为因变量，以2次拟合的结果为自变量，进行多元回归分析，考虑到交互作用，设函数模型为

f=α0+α1φ1+α2φ2+α3φ1φ2

(5)

式中:f为摩擦因数;α0、α1、α2、α3为待定常数。

按上述模型进行多元回归分析，得到回归结果的方差分析和回归模型，分别如表4、表5所示。

表4 摩擦因数多元回归方差分析Table 4 Analysis of variance of friction coefficient

表5 摩擦因数多元回归模型Table 5 Regression model of friction coefficient

表4中回归方程的自变量与因变量之间相关系数大于0.95，回归效果显著，显著性小于0.05，通过了F检验，因此可认为多元回归中的因变量和自变量之间具有显著的关系。表5回归模型中常量和φ1φ2项显著性小于0.05，表示这两项t检验通过，回归方程应包含这两项;φ1项和φ2项显著性大于0.05，表示这两项t检验未通过，不可应用于回归方程中。因此最后得到的回归方程为

f=0.028+6.907φ1φ2

(6)

为验证回归方程的准确性，设计3组不同配比试件，添加剂质量分数分别为4%/6%(即4% nano-La2O3/6%nano-serpentine，下同)、6%/18%和8%/12%，进行摩擦因数测试，测得实际摩擦因数与回归方程预测值误差分别为4.5%、3.2%和4.5%，均小于5%，验证了回归方程的准确性，证明预测可信。

根据多元回归方程，使用MATLAB软件求最优解，结果为：当nano-La2O3质量分数为3.89%，nano-serpentine质量分数为17.07%时，复合材料摩擦因数最低，为0.039 2。

为验证多元回归分析最优解的准确性，以该配比制作试件，进行摩擦学实验，测得实际摩擦因数为0.038 1，与回归方程预测值误差为2.81%，验证了回归方程的准确性，预测可信。此时，复合材料实际磨损率为9.75×10-6mm3/(N·m)。

2.2 最优磨损率

2.2.1 直观分析

试件磨损率随nano-La2O3、nano-serpentine质量分数变化分别如图6、图7所示。图6中，随着nano-La2O3质量分数的提高，磨损率基本呈上升趋势，当nano-La2O3质量分数低于7%时，复合材料磨损率相对较低。由图7可知，磨损率随nano-serpentine质量分数变化过程中同样存在2个极大值点和2个极小值点。综合图6、图7分析，为得到较低的磨损率，nano-La2O3质量分数应低于7%，nano-serpentine质量分数应在2个极值点附近。

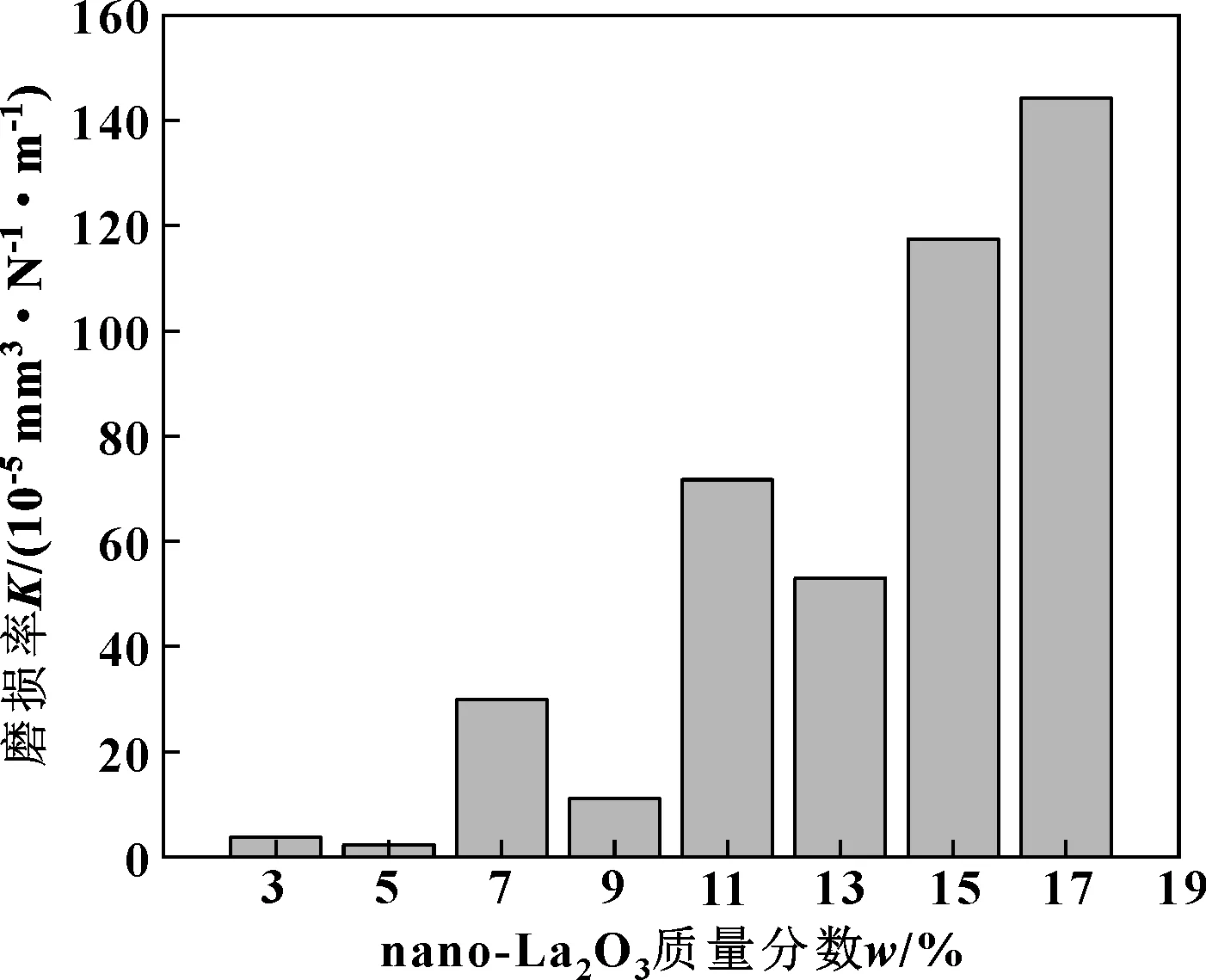
图6 磨损率随nano-La2O3质量分数的变化Fig 6 Variation of wear rate with nano-La2O3 mass fraction

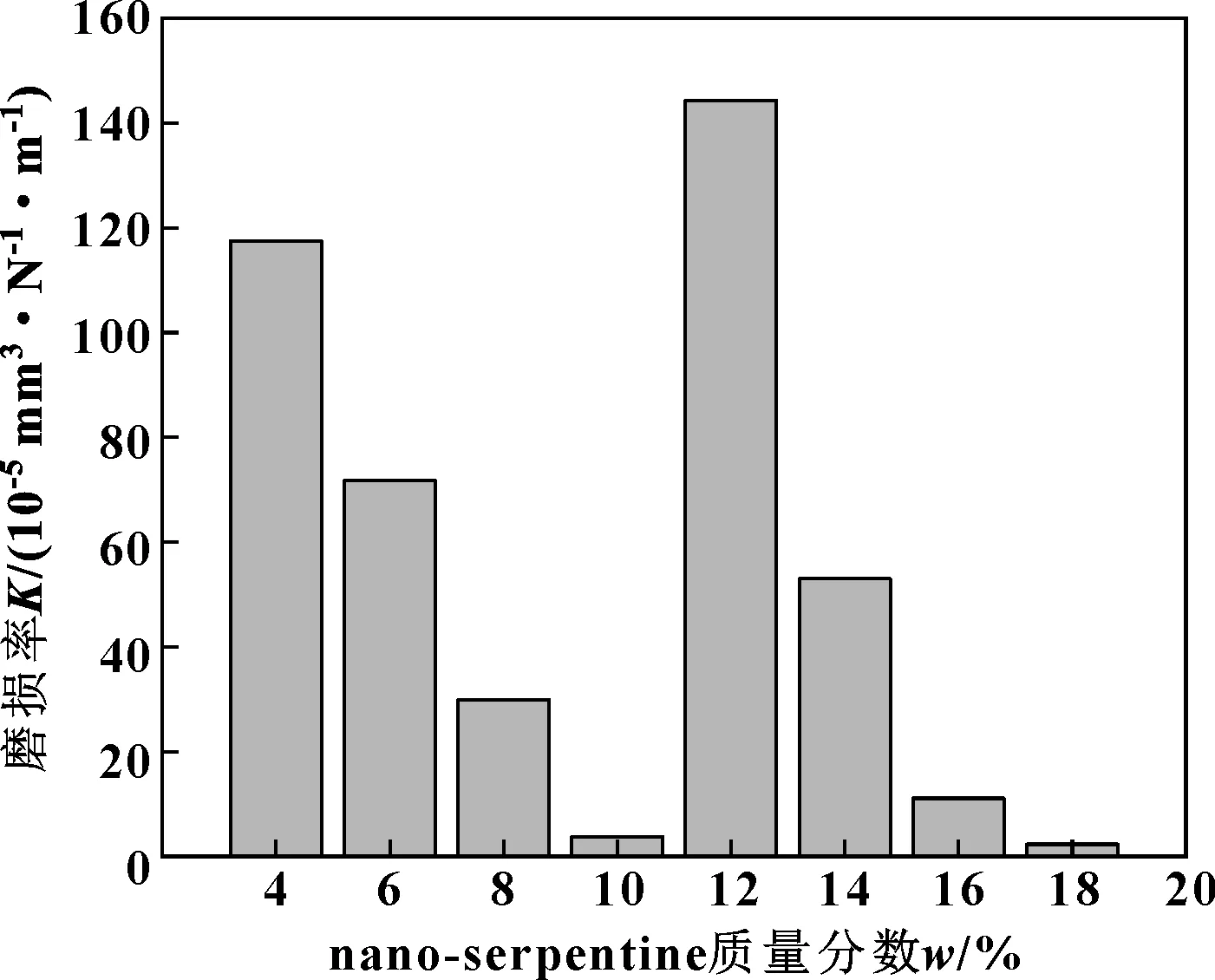
图7 磨损率随nano-serpentine质量分数的变化Fig 7 Variation of wear rate with nano-serpentine mass fraction

2.2.2 多元回归分析

方法同上，使用Origin软件分别对磨损率与nano-La2O3、nano-serpentine质量分数之间函数关系进行曲线拟合，拟合结果分别为

(7)

(8)

式中：θ1为nano-La2O3影响下的磨损率；θ2为nano-serpentine影响下的磨损率。

经检验，2个拟合结果显著性均小于0.05，通过了F检验，函数关系式拟合成功。

使用SPSS软件，以磨损率为因变量，以2次拟合的结果为自变量，进行多元回归分析，考虑到交互作用，设函数模型为

K=β0+β1θ1+β2θ2+β3θ1θ2

(9)

式中:K为磨损率;β0、β1、β2、β3为待定常数。

按上述模型进行回归分析，回归方程的方差分析和回归模型，分别如表6和表7所示。

表6 磨损率多元回归方差分析Table 6 Analysis of variance of wear rate linear regression

表7 磨损率多元回归模型Table 7 Regression model for linear regression of wear rate

方差分析表6中显示回归效果显著，显著性大小接近0，小于0.05，通过了F检验，所以磨损率与自变量之间存在显著的关系。表7中显示常量与θ1θ2项显著性小于0.05，通过了t检验；θ1项与θ2项显著性大于0.05，未通过t检验。因此将常量与θ1θ2项代入多元回归方程中，得到回归方程为

M=(0.816+0.008θ1θ2)×10-5

(10)

为验证回归方程的准确性，设计3组不同配比试件，其添加剂质量分数分别为4%/6%、6%/18%和8%/12%，进行磨损率测试，测得实际磨损率与回归方程预测值误差分别为7.9%、4.1%和8.7%，误差占比均小于10%，考虑到不同配比间磨损率大小相差可达到2个数量级，且预测磨损率变化趋势与实际磨损率变化趋势相同，故认为所预测回归方程可信。

根据所得的磨损率与nano-serpentine、nano-La2O3质量分数之间函数关系，利用MATLAB软件求出最优解，解得当nano-La2O3质量分数为3%，nano-serpentine质量分数为16.75%时，复合材料的磨损率最低，为8.3×10-6mm3/(N·m)。

为验证多元回归最优解的准确性，以该配比制作试件，进行磨损率测试，测得实际磨损率大小为8.65×10-6mm3/(N·m)，与回归方程的预测值误差为4.22%，验证了回归方程的准确性，预测可信。此时复合材料实际摩擦因数为0.039 1。

2.3 最优摩擦学性能

通过多元回归方程预测和实验验证可知：当nano-La2O3质量分数为3.89%，nano-serpentine质量分数为17.07%时，复合材料实际摩擦因数为0.038 1，实际磨损率为9.75×10-6mm3/(N·m)；当nano-La2O3质量分数为3%，nano-serpentine质量分数为16.75%时，复合材料实际摩擦因数为0.039 1，实际磨损率为8.65×10-6mm3/(N·m)。2种配比下复合材料摩擦因数相差2.6%，而磨损率相差11.3%，且磨损率的大小直接影响复合材料使用价值，因此综合确定，最优摩擦学性能为：f=0.039 1，K=8.65×10-6mm3/(N·m)，最优配比为：3%nano-La2O3， 16.75%nano-serpentine。

2.4 磨损表面形貌分析

磨损机制的不同对复合材料摩擦学性能具有极大影响，了解复合材料的磨损机制有助于分析其摩擦学性能优劣的原理，对确定复合材料最优性能和验证回归方程合理性具有十分重要的意义，如图8所示为不同水平复合材料磨损表面微观形貌。

图8 不同水平复合材料磨损表面微观形貌Fig 8 Microscopic topography of wear surface of composites with different levels (a)level 1(3% nano-La2O3，10% nano-serpentine);(b)level 2(5% nano-La2O3，18% nano-serpentine);(c)level 5(11% nano-La2O3， 6% nano-serpentine);(d)level 8(17% nano-La2O3，12% nano-serpentine)

由图8(a)、(b)可知，第1、第2两水平试件磨损表面光滑平整、犁沟较少，其中第1水平试件磨粒磨损与黏着磨损并存，第2水平试件只发生轻微的黏着磨损，磨粒磨损产生的划痕较轻。由图8(c)、(d)可知,第5、第8两水平试件磨损表面凹凸不平，发生了严重的黏着磨损，其中第8水平表面有许多较深的犁沟。分析认为：第1、第2两水平试件nano-La2O3质量分数相对较低，对复合材料摩擦因数负面影响较小且有助于降低磨损率;第5、第8两水平试件nano-La2O3质量分数较高，复合材料中添加剂容易分散不均，同时PTFE基体含量相对减少，导致试件强度低易磨损。

比较图8中4 水平下的磨损表面微观形貌可知，第2水平试件发生黏着磨损程度最低，并且磨粒磨损较少，而其他水平试件均存在不同程度的黏着磨损和磨粒磨损。分析认为：serpentine中的硅、镁元素可增强复合材料的硬度和强度并降低摩擦因数[25-27]，而第2水平的nano-serpentine质量分数最高，因此复合材料摩擦因数相对较低，且第2水平的硬度、抗压强度和抗剪切能力得到了最大程度的增强，有效抑制了黏着磨损的产生并且减少了磨粒磨损，提高了复合材料的耐磨性能。

综上：质量分数不超过5%的nano-La2O3使复合材料摩擦学性能得到很大提升，高于11%的nano-La2O3会导致复合材料摩擦学性能变差，这与拟合方程φ1中La2O3质量分数取值较小时摩擦因数较低，以及θ1单调递增相吻合。当nano-serpentine质量分数为10%和18%时，复合材料黏着磨损较少，磨粒磨损产生的划痕较轻，磨损率较低，并且这2个质量分数大小接近回归方程φ2和θ2中存在的2个极小值点。复合材料表面磨损机制分析证明了回归方程具有一定合理性。

3 结论

(1)综合考虑复合材料摩擦因数及磨损率试验结果，质量分数3%nano-La2O3、16.75%nano-serpentine为复合材料最优配比，此时复合材料摩擦因数为0.039 1，磨损率为K=8.65×10-6mm3/(N·m)，且最优摩擦因数与最优磨损率预测误差均小于5%，验证了多元回归方程准确性。

(2)nano-La2O3质量分数低于9%时，复合材料拥有良好的致密性和自润滑性能，nano-La2O3质量分数高于11%时，复合材料会发生严重的黏着磨损，这与回归方程中φ1和θ1两函数走势相吻合；nano-serpentine质量分数为10%和18%附近的复合材料，黏着磨损较轻，犁沟较少，磨损率较低，这与回归方程φ2和θ2中2个极小值位置相呼应。磨损机制分析在一定程度上验证了多元回归方程的合理性。