考虑齿变形的迷宫密封泄漏特性流固耦合数值研究*
2021-03-30杜宸宇
孙 丹 周 敏 赵 欢 王 平 杜宸宇
(沈阳航空航天大学,辽宁省航空推进系统先进测试技术重点实验室 辽宁沈阳 110136)
迷宫密封被广泛应用于航空发动机等透平机械中,起着减少工作介质泄漏的作用[1-3]。当机组运行时,传统迷宫密封的静子与转子之间容易发生碰磨,进而严重影响密封件的封严性能。采用热塑性材料的密封齿因其出色的摩擦学性能,可以在高转速、高压比的工况下实现更紧密的间隙,现已逐渐应用于迷宫密封领域。但当结构参数和工况参数相同时,热塑性材料相比于金属材料更容易发生齿变形。因此,考虑齿变形的迷宫密封瞬态流固耦合数值研究具有重要的理论意义和工程实际应用价值。
科研人员采用数值模拟的方法研究了迷宫密封几何结构对其泄漏特性的影响规律。XU等[4-5]率先研究迷宫齿弯曲后的曲率等几何结构对密封泄漏量的影响。陈尧兴等[6-7]研究认为迷宫密封齿弯曲磨损导致密封径向间隙增大,进而影响了密封泄漏量。DOGU等[8]分析了转子转速对齿顶的磨耗现象,并研究了蘑菇齿式迷宫密封的流场分布和泄漏量。汤赫男等[9]研究了迷宫密封节流间隙、空腔深度、齿型夹角等主要尺寸参数对密封泄漏量的影响。汤赫男等[10]采用流固耦合分析方法研究了齿形角对迷宫密封性能的影响。秦自臻等[11]以聚醚醚酮(PEEK)材料的密封环为研究对象,建立了旋转密封流固耦合模型,仿真结果表明在载荷作用下,密封环的变形影响了密封面接触压力和流体压力的分布,但并未考虑不同材料密封齿变形后对其泄漏量的影响。学者们对迷宫密封泄漏特性数值研究大多是基于金属材料迷宫密封[12],对考虑齿变形的迷宫密封泄漏特性瞬态流固耦合数值研究较少。
本文作者建立了考虑齿变形的迷宫密封泄漏特性瞬态流固耦合数值求解模型,在验证求解模型准确性的基础上,研究了进出口压比对酚酞聚芳醚酮(PEKC)、聚醚醚酮(PEEK)、聚醚砜酮(PPESKca30)3种材料的迷宫密封流场分布、最大径向变形量、等效应力及泄漏特性的影响。
1 迷宫密封流固耦合理论分析
1.1 流固耦合建模理论
1.1.1 流体动力学模型
在文中瞬态流固耦合计算工况下,需要满足湍流流动守恒方程[13-14]

(1)
(2)
式中:ρ为密度;t为时间;p为压力;U为速度;u、v和w是速度U在x、y和z方向的分量;Г为扩散系数;Su、Sv和Sw为动量守恒方程的广义源项,即
(3)
其中,Fx、Fy和Fz为体力,若体力只有重力,且z轴竖直向上,则Fx=0、Fy=0和Fz=-ρg;μ为动力黏度;λ是第二黏度,一般可取λ=-2μ/3。
当采用了高性能热塑性材料的密封齿受到气动载荷作用弯曲变形时,流场变得十分复杂。文中需要对标准k-ε模型进行修正[13],修正模型RNGk-ε模型为
(4)
(5)
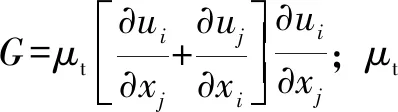
由式(1)—(5)可知,RNGk-ε模型能够更准确地求解迷宫密封流场复杂的流体流动。
1.1.2 结构动力学模型
迷宫密封热塑性密封齿在流体作用下的响应可通过求解结构动力学方程获得[15],即为
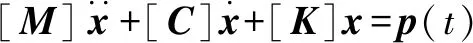
(6)
即
(7)
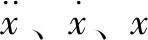
1.1.3 流固耦合分析
文中建立了考虑材料的迷宫密封齿变形瞬态流固耦合求解模型,利用CFX和Transient Structurl进行双向流固耦合计算。为了提高数值结果的计算精度,文中求解采用守恒插值法,若密封齿网格位移为Xs,通过传递函数[T]将密封齿网格位移转换为流场的网格位移Xf,表达式[15]如下
Xf=[T]Xs
(8)
(9)
Fs=[T]TFf
(10)
式中:Ff、Fs分别为作用在耦合面上的流体与密封齿载荷。
迷宫密封瞬态流固耦合求解采用双重循环迭代方法[16]。如图1所示,从Tn时刻开始循环,以Tn+1时刻的流场分布和密封齿变形的位移作为初始条件,流体域计算结果收敛后,通过网格插值将得出的流场分布信息传递给密封齿固体域耦合面上,密封齿耦合面以其为边界条件进行计算得到密封齿动力响应,直至流体域与固体域都达到收敛时,则完成一次耦合迭代计算。
2 迷宫密封瞬态流固耦合结构分析
2.1 几何模型
文中计算模型取自文献[17]的压缩机叶轮入口迷宫密封,建立了瞬态流固耦合数值求解模型,该模型包含5个齿高、齿厚均相等的锥形直齿,齿顶与转子之间的间隙将密封分为4个密封腔。密封齿材料采用聚芳醚酮。聚芳醚酮可用来制造压缩机梳齿密封、航空航天结构材料等。迷宫密封几何参数如图2所示。迷宫密封结构如图3所示。密封齿材料参数见表1。
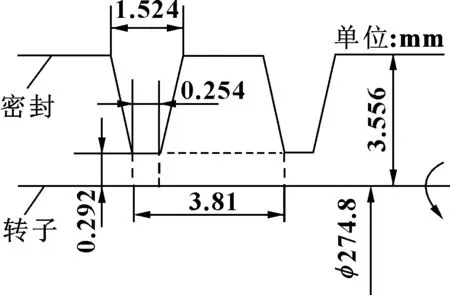
图2 迷宫密封模型尺寸Fig 2 Size of labyrinth seal model

图3 迷宫密封结构Fig 3 Labyrinth seal structure
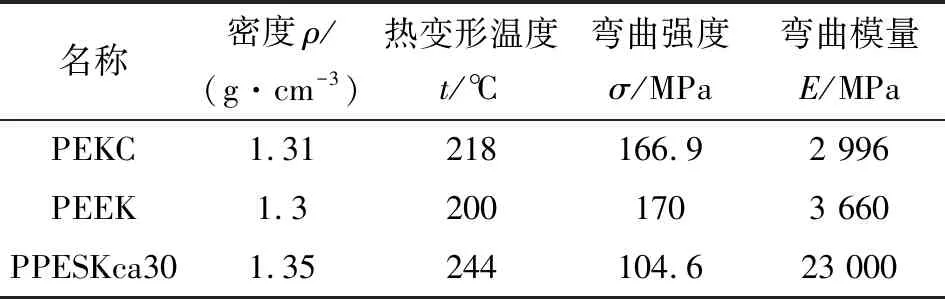
表1 密封材料力学性能Table 1 Mechanical properties of sealing materials
2.2 网格划分
密封流场和固体结构均采用六面体结构化网格。图4所示为迷宫密封流固耦合网格划分结果。选择不同的网格密度进行网格无关性验证,以密封泄漏量为特征参数选取最合理的网格数量,结果如图5所示。最终,网格数量选取980万。综合考虑求解精度及计算时间,最终确定流体周向节点数为250,密封齿腔的轴向节点数为50,密封齿腔的径向节点数为25,齿顶间隙处的轴向节点数设置为10,齿顶间隙处的径向节点数设置为15,所得流体网格数目为980万。采用相同方法可以确定固体周向节点数100,密封齿腔的轴向节点数为10,密封齿腔的径向节点数为20,最终确定固体网格数目为350万。
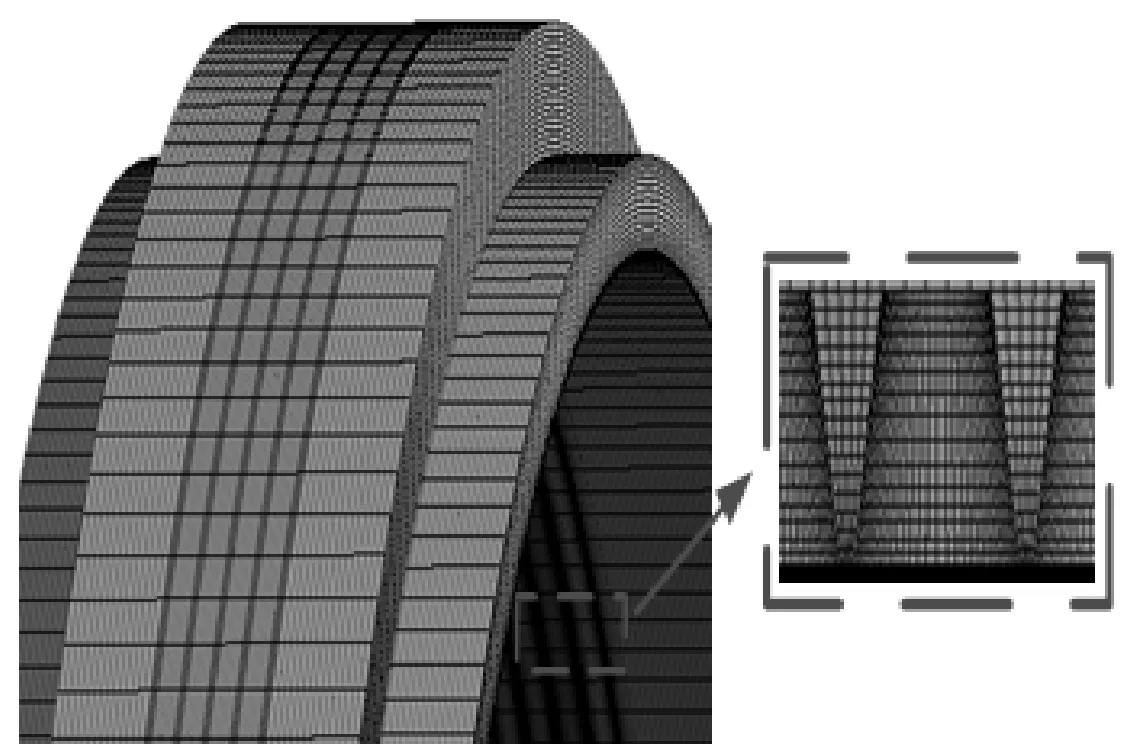
图4 迷宫密封流固耦合网格划分Fig 4 Fluid-structure interaction mesh division of labyrinth seals

图5 密封泄漏量与网格数量关系曲线Fig 5 Relation curve between seal leakage and mesh number
2.3 边界条件及求解方法
文中模型流体域进口设置为总压,出口设置为静压,进出口压比为3~7。求解模型为同心涡动模型,流体流动模型为k-ε湍流模型,固定壁面为光滑、绝热、无滑移边界,采用高精度迎风格式进行迭代计算。当连续、动量、湍流方程残差下降到10-6,认为计算收敛。图6(a)给出了密封流体边界条件。
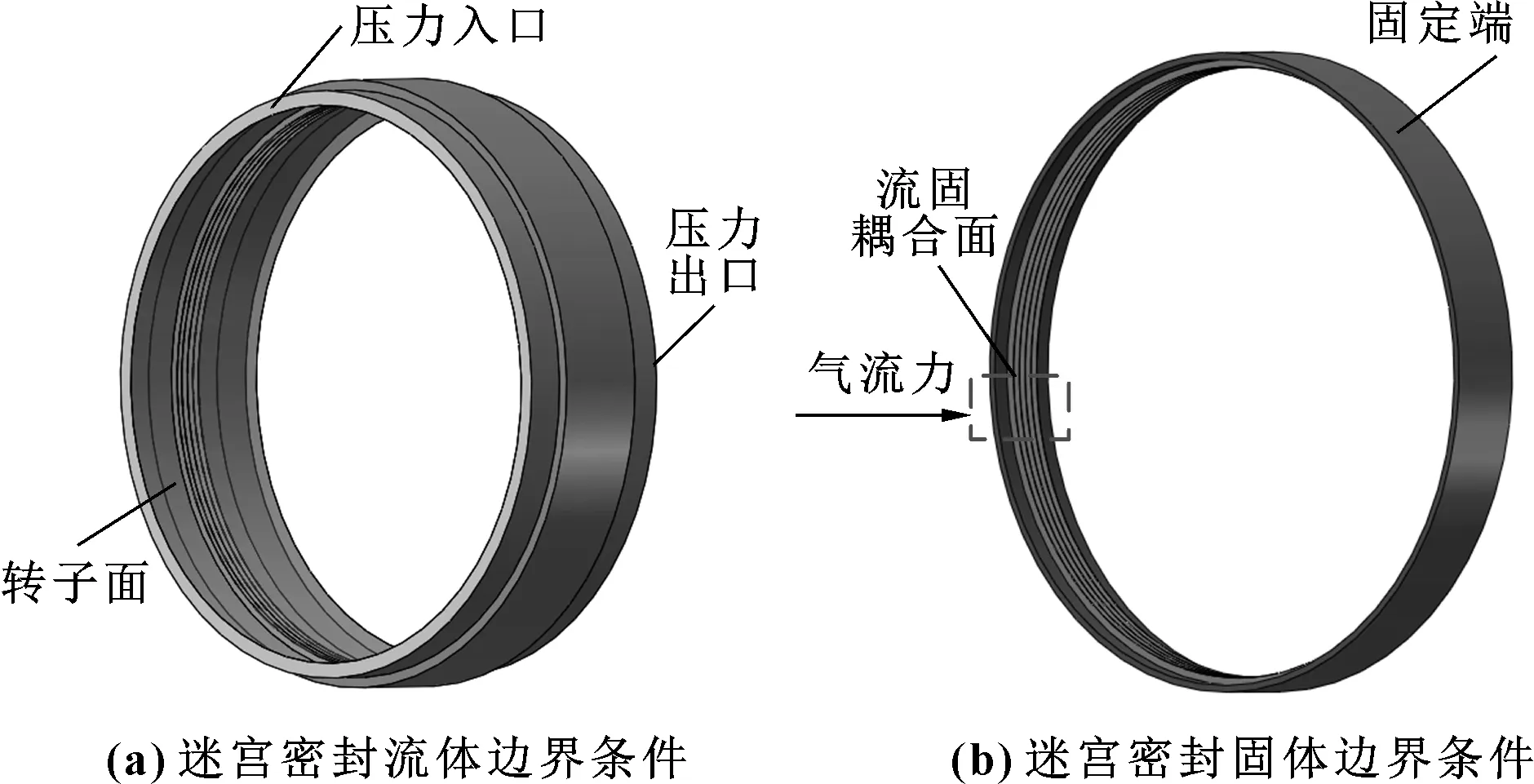
图6 流固耦合边界条件Fig 6 Boundary conditions of fluid-structure interaction (a) labyrinth seal fluid boundary conditions;(b) labyrinth seal solid boundary conditions
文中模型固体域采用3种不同性能聚芳醚酮材料(见表1),密封结构的固定端采用固定约束,将密封齿表面设定为流固耦合面。耦合面通过导入流场计算收敛后的气流力以实现流固耦合的载荷传递,从而将流场的压力数据通过节点数据导入固体中计算。图6(b)给出了密封固体边界条件。密封模型的具体工况参数见表2。
双向流固耦合通过设置流固耦合面,将所有需要传递的数据在此交界面上进行插值传递。
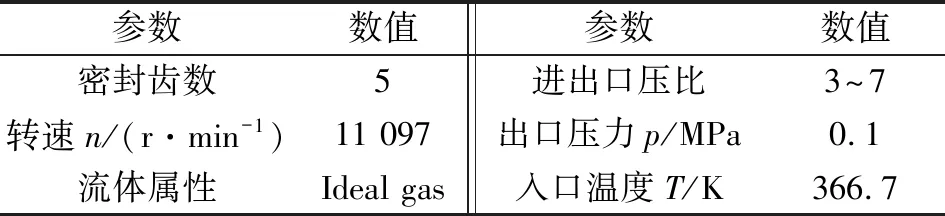
表2 密封模型工况参数Table 2 Operating parameters of seal model
2.4 求解模型准确性验证
表3给出了文中CFX模型与标准文献基于双控制体法建立的DYNLAB模型和Tascflow模型[17]的密封泄漏量求解结果,图7给出了其对应的密封周向压力分布的对比。

表3 密封泄漏量计算结果对比Table 3 Comparison of seal leakage calculation results

图7 不同求解方法轴向压力变化比较Fig 7 Axial pressure change comparison of different calculation methods
通过压力分布情况和泄漏量的对比,可以得出双控体模型在求解密封的流场特性时误差较大,主要是因为双控体方法在简化方程的同时缺少对具体流动的描述和方程求解,忽略了密封齿顶间隙处的流动情况。CFX求解模型得到的流场特性结果与Tascflow的结果相近,表明CFX模型能较好地解决实际工程问题。从表3中可以看出,2种方法所求得的密封泄漏量相对误差为0.93%。文中数值计算得到的泄漏量、轴向压力分布与标准文献数值计算结果误差较小,验证了求解模型的准确性。
3 数值求解结果及分析
3.1 密封流场特性分析
3.1.1 密封流场压力分布
图8给出了进出口压比为6,迷宫密封考虑材料(PEKC)密封齿变形和未考虑材料密封齿变形时,密封内的流场压力分布。可以看出,密封内流场压力沿轴向逐渐降低,在齿腔内的压力分布基本一致,且齿顶处的压力稍高于齿腔内压力。比较图8(a)、(b)可以得出,考虑齿材料变形的流场中最后一节齿顶处的压力要低于其相同工况下未考虑齿材料变形的流体压力。因为压力能从入口到出口是逐渐降低的,且在齿尖处形成流束收缩效应,压力降低,速度增大,压力能转化为动能。

图8 密封流场压力云图Fig 8 Pressure cloud diagram of sealing flow field (a) without considering tooth material deformation; (b) considering tooth material deformation
3.1.2 密封流场速度分布
图9给出了进出口压比为6,迷宫密封考虑齿材料(PEKC)变形和未考虑齿材料变形时,密封内的流场速度分布。可以看出,迷宫密封中的流场分为射流区和漩涡区,正是齿顶的这种节流和密封腔内的动能耗散起到了密封作用。在轴向上的速度分布基本均匀,气流经过密封后速度有所增加。在密封齿腔中的气体流动呈明显的漩涡状,且密封齿根处的速度明显小于齿顶处的速度。由图9可以进一步得出,流体流速的最大值都是在迷宫密封最后一节齿的齿顶处。比较图9(a)、(b)可以得出,考虑齿材料变形的流场中最后一节齿顶处的速度要明显高于其相同工况下未考虑齿材料变形的流体流速。速度云图的分布情况与实际密封结构工作时的速度分布相同。

图9 密封流场速度云图Fig 9 Velocity cloud diagram of sealing flow field (a) without considering tooth material deformation; (b) considering tooth material deformation
3.2 密封结构力学特性分析
3.2.1 密封结构变形
图10(a)给出了进出口压比为7,迷宫密封采用PEEK材料时密封结构变形分布。图10(b)给出了进出口压比在3~7变化范围内,迷宫密封分别采用3种不同性能聚芳醚酮材料时,密封齿最大径向变形量随压比的变化。
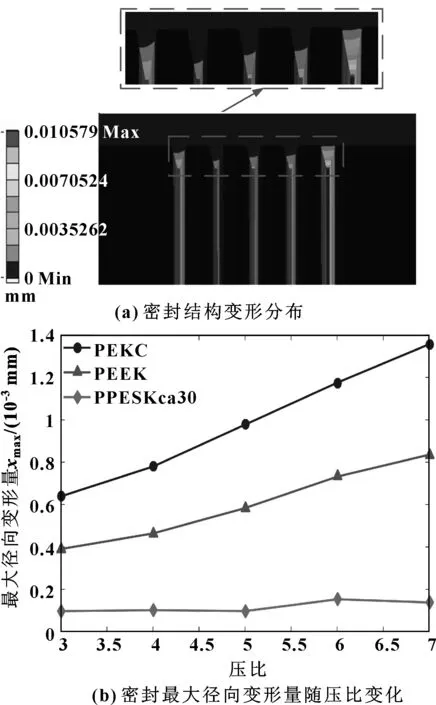
图10 密封结构变形分布和最大径向变形量随压比变化Fig 10 The deformation distribution of sealing structure and the variation of the maximum radial deformation with pressure ratio (a) deformation of sealing structure;(b)variation of the maximum radial deformation of the seal with pressure ratio
从图10(a)中可以看出,密封件最大变形量出现在最后一个齿的齿顶位置,且每个密封齿的变形量均从其齿顶位置向齿根方向逐渐减小。从图10(b)中可以看出,随着压比的增加,密封径向最大变形量增大,从而导致密封径向间隙增加。在相同压比下,采用PPESKca30、PEEK、PEKC齿材料的迷宫密封件径向最大变形量由小到大。
3.2.2 密封结构应力
图11(a)给出了进出口压比为7,迷宫密封采用PEEK材料时密封结构应力分布。图11(b)给出了进出口压比在3~7变化范围内,迷宫密封分别采用3种不同性能聚芳醚酮材料时,密封等效应力随压比的变化。
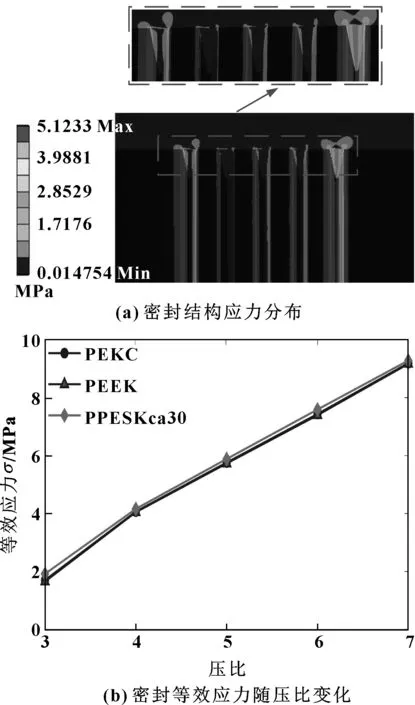
图11 密封结构应力分布和等效应力随压比变化Fig 11 The stress distribution of sealing structure and the variation of the equivalent stress with pressure ratio (a) sealing structure stress;(b) variation of the equivalent stress of the seal with pressure ratio
从图11(a)中可以看出,等效应力主要集中在密封齿上。密封件等效应力的最大值分布在最后一个密封齿的齿根位置,且每个密封齿的等效应力均从齿根处向齿顶方向逐渐减小,故密封齿的齿根位置最容易断裂。密封结构的最大应力值均小于所用材料的弯曲强度,故密封结构在文中工况下不易产生材料屈服和结构被破坏的情况,可满足该工况下的使用条件。从图11中(b)可以看出,随着压比的增加,密封等效应力增大。在相同压比下,采用PPESKca30、PEEK、PECK齿材料的迷宫密封件等效应力基本不变,引起材料屈服的主要因素是畸变能密度。
3.3 密封泄漏特性分析
当机组实际运行时,采用高性能热塑性材料的密封齿受到气流力的作用,会导致密封齿发生形变,密封径向间隙将会变大,进而影响密封的泄漏特性。图12给出了迷宫密封考虑齿材料变形和未考虑齿材料变形的泄漏量对比。可以看出,随着压比的增加,密封径向间隙将会增大,从而导致密封泄漏量增加;在相同压比下,采用PPESKca30、PEEK、PECK齿材料的迷宫密封件的泄漏量由小到大。由材料力学性能参数可知,变形量主要和材料的弹性模量有关,弹性模量越小,密封齿径向变形越大,导致密封泄漏量增大。由密封流场速度图也可得出,考虑齿材料变形的泄漏量高于未考虑齿材料变形的泄漏量。文中研究的3种材料中,PPESKca30的变形量最小,密封泄漏量也最少。
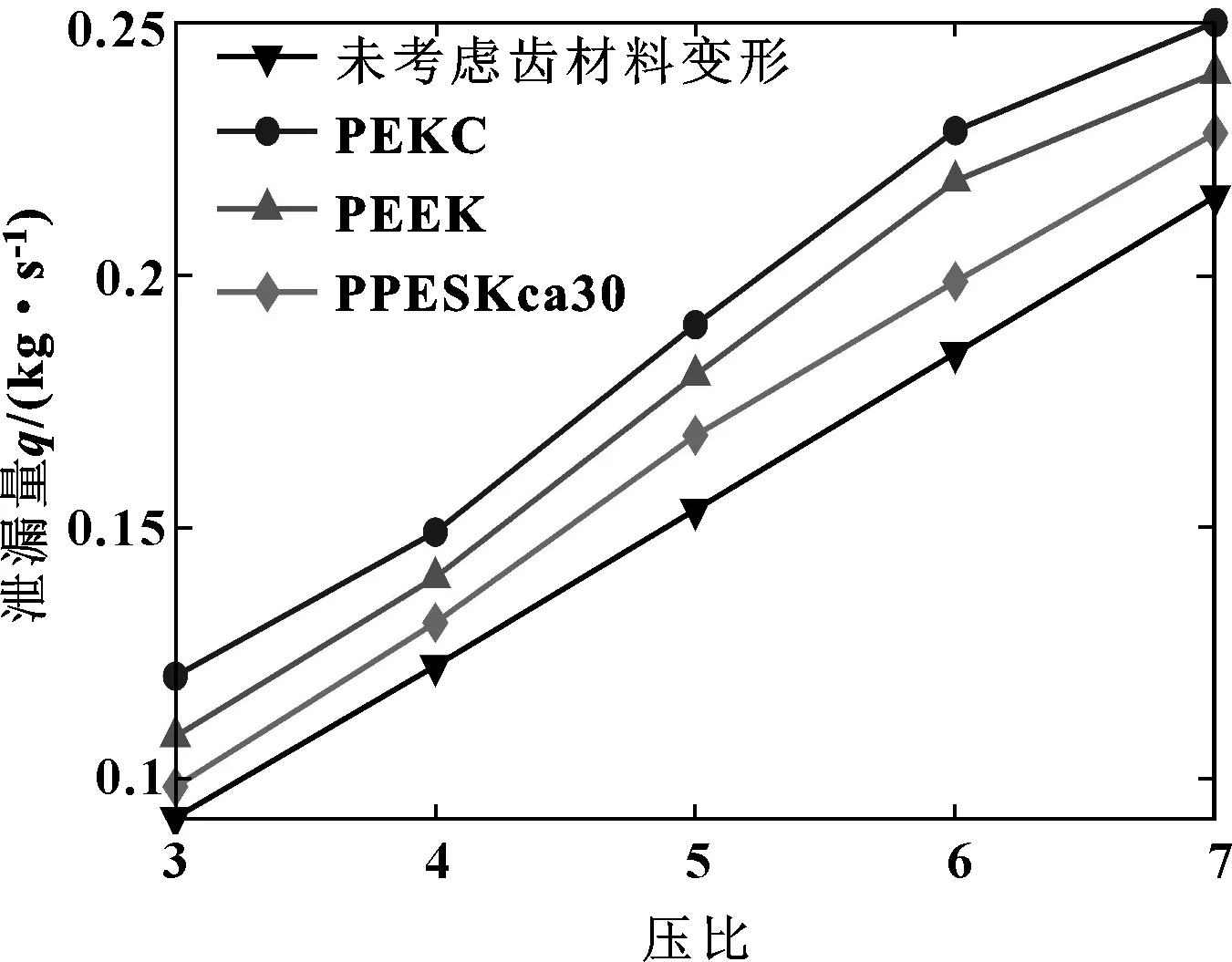
图12 迷宫密封泄漏量对比Fig 12 Comparison of labyrinth seal leakage
4 结论
(1)考虑齿变形的密封流场中最后一节齿顶处的压力要低于其相同工况下未考虑齿变形的流体压力,而速度则恰好相反。
(2)密封件最大变形量均出现在齿顶位置,且从其齿顶位置向齿根方向逐渐减小。密封件等效应力的最大值均分布在齿根位置,且从其齿顶位置向齿根方向逐渐增大。
(3)在进出口压比为3~7下,密封齿受到气流力作用发生变形,密封径向间隙增大,导致泄漏量增加了6.6%~30%。
(4)当进出口压比相同时,材料的弹性模量越大,密封齿变形越小,封严性能越好。文中研究的3种材料中,PPESKca30的变形量最小,密封泄漏量也最少。
