慢『漫』地教数学——『慢』是拓宽思考的角度

文 孙贵合

“横看成岭侧成峰，远近高低各不同。”角度不同，便能欣赏到不同的风景。但为什么我们总看不到新的风景？“不识庐山真面目，只缘身在此山中。”因为我们习惯了用一个角度、一个方向去看待问题。当一个人对一件事情有了认识之后，总是习惯性地按照自己原有的方式去思考，很难再从不同的角度和方向去思考解决这件事情的其他方法。思维定势在心理学上是指人在进行心理操作活动中的一种准备状态，定势表现为问题解决过程中的思维倾向性，常按照自己已经掌握的或者熟悉的方法去解决问题。但当一个人面对一件新的事物时，不会被思维定势影响，因此考虑问题会有很多不同的方向，这时是“头脑风暴”式的思考，因此会出现很多我们想都没有想过的方法，这也是教育真正的意义。同时如果运用得当，还能够为教学带来意想不到的效果。在教学时，教师由于多年的学习和教学经验对知识本身产生了思维定式，因此当学生有了新的角度，很多时候会被教师所扼杀，所以教师更应该多听一听学生的发言，从而也让我们自己有更多思考的角度。

案例《圆的面积》。

在教学这节课的时候，我让学生思考：圆是一个曲线图形，那要计算它的面积，你有什么办法？

生1：我可以把圆一点一点地分割成很多小正方形或小长方形，然后一个个地计算出它们的面积，便可以得到圆面积的近似值。（微分的思想，无限分割。这也是人类最开始计算圆的面积的方法）

师：这是一种很好的方法，但操作起来好像很麻烦，还有不同的方法吗？

生：我们可以把圆的面积转化成我们所学过的图形的面积，然后再进行计算。比如长方形、正方形、三角形、梯形、平行四边形等。

师：这个同学结合了我们以前所学过的图形，把一个新的图形转化成以前所学过的图形，然后再计算，这是一种很好的方法。而且“转化”也是数学中很重要的一种思想。关于“转化”还有这样一个小故事：一天，消防员觉得数学家的工作不错，于是他跑到数学家面前问：“您看看我有没有当数学家的潜质？”数学家说：“您看上去不错，可是您要回答我两个问题。”消防员说：“行，您问吧。”数学家说：“巷子里有一个货栈，一只消防栓和一卷软管。货栈起火，您怎么办？”消防员回答：“我把消防栓接到软管上，打开水龙头，把火浇灭。”数学家说：“完全正确！最后一个问题：假设您走进小巷，而货栈没有起火，您怎么办？”消防员疑惑地思索了半天，终于答道：“没着火，那我就回去了。”数学家说：“那你可以回去了，你不适合做数学家。”消防员问：“那数学家会怎么解决呢？”数学家回答：“如果是数学家解决这个问题，那得把这个房子点着了，这样我就把问题转化为一个我已经解决过的问题了。”可见“转化”的思想多么重要。好，那同学们自己动手尝试一下吧！

（学生操作，把圆转化成以前所学过的平面图形，并结合面积计算中各部分之间的关系，推导出圆的面积计算公式）

生：老师，我把圆的面积转化成了长方形。（因为是常用的推导方法，所以具体推导过程略）

生：我把圆的面积转化成了三角形的面积。（如图1）

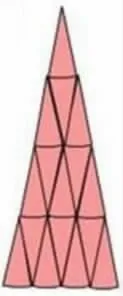
图1

生：把一个圆平均分成十六等份，然后拼出了一个近似的三角形，这个三角形的底就是圆周长的四分之一，高就是四个半径，这样三角形的面积便得到了：

生：老师，我还可以把圆的面积转化成梯形的面积。（具体方法略）

生1：老师，还用刚才我的方法——分成很多小正方形，这是我想的但我没做出来，就是在圆里画很多小的正方形，然后在圆外面再画一个大的正方形，数一数圆里有多少个小正方形，然后看一看大正方形里有多少个小正方形，便能得到圆的面积占正方形面积的几分之几，因为正方形的面积是能够计算的，所以也能够计算出圆的面积。

师：那你能够找到圆的面积公式吗？

生1：没有找到。

师：你的方法很好，但我们还是转化成以前所学过的图形的面积更简便。

把圆的面积转化成长方形、三角形、梯形等都在教师的意料之中，这也是提前就准备好的，因为不转化成这样的图形学生是没办法得到圆的面积公式的。对于生1 的想法，教师也给予了充分的肯定，但并没有引起足够的重视，认为这种方法不能计算圆的面积。后来在无意中了解数学史，看到了这样一幅图片和文字说明：

早在公元前1650年，埃及草纸文献中就记载了圆的面积计算方法。人们用大小均匀的麦粒将图2 铺满，分别数出正方形和圆形里的麦粒，算出圆面积大约是正方形面积的九分之八。这已经很接近现在圆的面积πr2。而且这里面包含了大量的数学思想和文化，这也是人类认识世界最基本的思想。如果想要得到圆面积更精确的结果，可以把麦粒变成小米，这也就是单位细化的思想。许多知识的发展都是单位细化的过程，为什么有了一位小数还要有两位、三位小数，有了长度单位“米”还需要分米、厘米、毫米，这都是为了得到更加精确的结果在进行单位细化。而且在这个过程中真正体现了“转化”的思想：要计算圆的面积，但不直接计算圆的面积，而是转化成计算圆与正方形之间的关系。其他的几种方法中也有转化：把圆转化成长方形、平行四边形、三角形等等，但都是同一类别的转化。而这种转化才是真正地用一种中间量来进行比较，这种转化才是真正解决生活中问题的最有用的转化思想。曹冲称象，把大象转化成了石头；希腊学者阿基米德为国王鉴定过一顶王冠，看它是否是纯金制成的，把这个问题转化成了体积与质量的比；买同等材质的毛线，哪一卷长，可以转化成称重量等等，这些生活中真正的转化才是我们学习的目的。如果在课堂中慢下来，让学生把话说完，把想法加以细化，我想收获会更大，因为学生全新的角度，也会给教师带来新的思考、新的突破。所以课堂是师生共同成长的舞台，“弟子不必不如师，师不必贤于弟子”，“慢”下来，让学生带我们从不同的角度欣赏数学的美。

图2