求解一类模糊线性系统的全局FOM和GMRES方法
2021-03-30葛志利
顾 颖,葛志利,陈 新
(1.宿迁学院文理学院,江苏 宿迁 223800)(2.南京科技职业学院基础科学部,江苏 南京 210048)(3.南京师范大学数学科学学院,江苏 南京 210023)
自1965年Zadeh在文[1]中首次提出模糊集概念,模糊数学作为一门新兴学科迅速发展起来,现已成为一个独立的数学分支,在工程分析、模式识别、自动控制、经济、金融等领域发挥着重要的作用[2-3]. 上述领域中许多问题最终都可转化为线性方程组,如平衡态和稳态问题的有限元法,就产生了一族联立代数线性方程组. 即使是非线性问题,我们也希望在某种意义下能够转化为线性问题. 同时,由于实际问题中往往含有许多不确定因素,无法用精确数据来刻画,常需借助模糊数来描述这种不确定性. 因此,实际应用中出现较多的通常是参数全部或部分为模糊数的线性系统,我们称其为模糊线性系统.
本文考虑一类用处较广的n×n阶模糊线性系统,其系数矩阵是精确数矩阵,右端项为模糊数向量. 文[4]中首次提出求解该类型系统的一个通用模型,即利用嵌入方法将原模糊系统转化为2n×2n阶精确线性系统. 在此基础上,文[5-9]的作者相继提出了求解这类系统的诸多迭代法,如Jacobi,Gauss-Seidel,SOR,SSOR,Richardson,AOR,EMA,MSOR方法等. 由于精确线性系统含有参数,即是一个符号系统,因此,上述以它为模型建立的算法在处理实际问题时往往需计算两个独立的数值系统,如文献[9]中的算例,这就大大增加了计算成本. 为解决这一问题,文[10]依据LR-梯形模糊数[11]的特点,将精确线性系统进一步转化为不含参数的矩阵方程,并依据新模型重新建立了Jacobi和Gauss-Seidel迭代法. 基于矩阵方程模型的算法在计算时仅需处理一个数值系统,计算量约为基于精确线性系统模型的同类型算法的一半.
文[12]提出的完全正交化方法(FOM)和广义极小残量法(GMRES)是目前求解线性系统最有效的方法之一. 文[13]进行了推广,建立了求解矩阵方程的全局完全正交化方法(Gl-FOM)和全局广义极小残量法(Gl-GMRES). 本文将它们应用于模糊线性系统的矩阵方程模型,提出求解该系统的两种新的数值方法,并给出收敛性分析. 最后,数值结果验证了新方法的稳定性与有效性.
1 预备知识
在这一节里,我们将给出一些关于模糊线性系统以及矩阵方程模型的概念和结论.
定义1[4-6]称有序函数对(u(r),u(r)),0≤r≤1为模糊数,若它满足以下3个条件:
(1)u(r)是[0,1]上的有界左连续非减函数;
(2)u(r)是[0,1]上的有界左连续非增函数;
(3)u(r)≤u(r),0≤r≤1.
对任给的模糊数x=(x(r),x(r)),y=(y(r),y(r))(0≤r≤1)和实数k有如下运算关系:
(1)x=y当且仅当x(r)=y(r),x(r)=y(r);
(2)x+y=(x(r)+y(r),x(r)+y(r));
定义2[4]考虑n×n阶线性方程组
其矩阵形式为
Ax=y,
(1)
系数矩阵A=(aij)(1≤i,j≤n)是精确数矩阵,右端是由模糊数yi(1≤i≤n)构成的向量,称系统(1)为n×n阶模糊线性系统.
定义3[4-6]模糊数向量x=(x1,x2,…,xn)T(其中xi=(xi(r),xi(r)),1≤i≤n,0≤r≤1)称作模糊线性系统(1)的解,如果成立

若令


则模糊线性系统(1)等价于2n×2n阶精确线性系统

(2)
系数矩阵

(3)
矩阵B包含了A中的正元,矩阵C包含了A中负元的绝对值,显然,A=B-C. 具体可参考文献[4].
引理1[4]矩阵S非奇异当且仅当A=B-C和B+C都是非奇异的.
注1引理1表明即使(1)的系数矩阵A非奇异,S仍有可能奇异.
注2引理1虽保证了当B+C,B-C均非奇异时(2)有唯一解,但此解未必是模糊数向量.
定义4[4-6]设x={(xi(r),xi(r)),1≤i≤n}是由(2)得到的模糊线性系统(1)的唯一解,如果(xi(r),xi(r))(1≤i≤n)全都是模糊数,则称x为强模糊解;否则,称作弱模糊解.
文献[10]依据LR-梯形模糊数的结构特征:
x=(x(r),x(r))=(x1+x2r,x3-x4r),
(4)

将系统(2)进一步转化为不带参数的矩阵方程
SX=Y.
(5)
至此,求解模糊线性系统(1)就转化为求解矩阵方程(5). 同时,考虑到S的分块结构,从优化算法的角度考虑,我们将X和Y也表示成类似形式. 令
即
从而,矩阵方程(5)等价于
(6)
2 全局Arnoldi过程
对任给矩阵V∈R2n×2,定义矩阵Krylov子空间Kk(S,V)=span{V,SV,…,Sk-1V},本节根据文献[13]中算法2.2建立全局Arnoldi算法,构建Kk(S,V)的一组F-正交基. 同时,考虑到模糊线性系统的矩阵方程模型(6)的特殊结构,将算法中的初始矩阵V和基V1,…,Vk均处理成分块形式,即
算法1全局Arnoldi算法
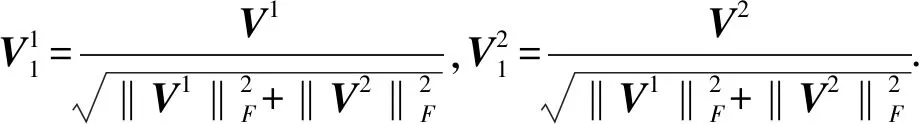
2.forj=1,…,k
4. fori=1,…,j
7. end
10. end


(7)

(8)

(9)
因为
其中
(10)
所以
(11)
结合式(9)和式(11),得到
故式(7)得证. 式(8)类似可证得.
3 Gl-FOM和Gl-GMRES方法
考虑模糊线性系统的矩阵方程模型(5),根据文献[13]中求解一般矩阵方程的Gl-FOM和Gl-GMRES方法的思想,设X0表示初始矩阵,对应残量为R0=Y-SX0,迭代法在第k步的近似解Xk具有如下形式:
(12)
式中,yk∈Rk为待定向量.

在Gl-GMRES方法中,要求Rk满足Rk⊥FKk(S,SR0),该正交条件可转化为最小二乘问题
(13)
由于算法1生成的基是F-正交的,为便于实际计算,(13)可用一规模较小的最小二乘问题
(14)
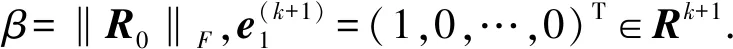
考虑到矩阵方程模型(5)或(6)的特殊结构,为节省存储空间,减少计算量,采用与算法1类似的做法,将初始矩阵X0和第k步近似Xk也表示成分块形式,即
从而,第k步残量
算法2Gl-FOM和Gl-GMRES方法


由于在计算过程中需存储矩阵Krylov子空间Kk(S,R0)的一组基V1,…,Vk,随着k的增大,存储量也在变大,计算时便会出现近似解还没达到预设精度,但k已不能再增大的情形. 为解决这一问题,Jbilou等人[13]采用重启策略,具体做法是预先给定一个不太大的正整数k,根据算法2求得近似解Xk,若该近似解达不到精度要求,则以其作为下一次计算的初始值,即带重启策略的Gl-FOM和Gl-GMRES方法,记作 Gl-FOM(k)和Gl-GMRES(k). 该类方法总的迭代次数为内迭代次数k与重启次数的乘积.
接下来,对Gl-FOM和Gl-GMRES方法在第k步迭代时的残量Rk的上限作出估计.
定理2Gl-FOM方法在第k步迭代时所得的残量Rk满足以下关系
(15)
(16)



定理3Gl-GMRES方法在第k步迭代时所得的残量Rk满足以下关系
证明参照文献[13].
4 数值实验
本节,我们测试了算法的数值结果. 所有程序均用MATLAB R2016a语言编写,且在win10系统下运行.
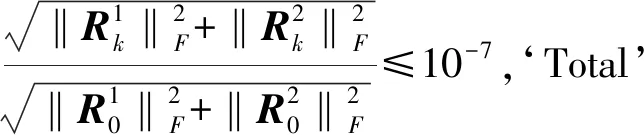
例1考虑n×n阶模糊线性系统Ax=y,其中
本例中A是严格对角占优矩阵,由文献[10]定理4知,Jacobi和Gauss-Seidel方法都收敛. 不难判断B+C,B-C均是非奇异矩阵,由引理1得,S也是非奇异的. 分别就n取100,200,300的情形进行计算,数值结果见表1.

表1 Gl-FOM(10),Gl-GMRES(10),Jacobi和Gauss-Seidel方法的数值结果Table 1 Numerical results of Gl-FOM(10),Gl-GMRES(10),Jacobi and Gauss-Seidel methods
从表1能够看出,当模糊线性系统阶数相同时,Gl-FOM(k)和Gl-GMRES(k)方法所需总的迭代次数和时间远少于Jacobi和Gauss-Seidel方法,且随着系统规模增大,差距越明显.
例2考虑n×n阶模糊线性系统Ax=y,其中
根据A的表示,容易判断B+C,B-C均非奇异,由引理1知,S也是非奇异的. 文献[9]中,就n取100,200,300的情形进行了计算,本文考虑更大规模的情况,即n分别取300,400,500,数值结果见表2.

表2 Gl-FOM(10),Gl-GMRES(10),Jacobi和Gauss-Seidel方法的数值结果Table 2 Numerical results of Gl-FOM(10),Gl-GMRES(10),Jacobi and Gauss-Seidel methods
从表2数据能够看出,本文的Gl-FOM(k)和Gl-GMRES(k)方法花费较少的迭代次数和时间即可达到预设精度,但Jacobi和Gauss-Seidel方法对本例无效.
5 结论
对于n×n阶系数矩阵是精确数矩阵,右端项为模糊数向量的模糊线性系统,本文基于矩阵方程模型建立了求解该系统的Gl-FOM和Gl-GMRES方法,并对这两种方法作了收敛性分析. 数值结果验证了新方法明显优于Jacobi和Gauss-Seidel方法[10].
