低温推进剂贮箱气冷屏复合绝热结构综合优化设计

2021-03-29余建榕康慧芳章丹亭

真空与低温 2021年2期

余建榕，张强，康慧芳*，章丹亭

（1.北京理工大学机械与车辆学院热能工程研究所，北京 100081；2.北京航天动力研究所，北京 100076）

0 引言

随着航天技术的不断发展，大型运载火箭低温推进剂贮箱越来越受关注。液氢/液氧低温推进剂是目前性能最高的推进剂，但其沸点低，极易蒸发，难以长期贮存，因此限制了其长时间在轨使用。低温火箭末级受到复杂外热流的影响，必须通过各种隔热措施使外界向低温贮箱的漏热量达到最小，以减少低温推进剂长期在轨过程中的损耗。

针对空间飞行器推进剂低温贮箱的绝热问题，美国NASA低温技术研究者在原有多层绝热技术基础上提出的聚氨酯泡沫（SOFI）/变密度多层绝热（VD-MLI）新型组合绝热结构具有绝热效果佳、质量小等优点，且能兼顾贮箱在太空中和地面上的绝热要求，是未来太空飞行器低温贮箱绝热结构的发展方向[1]。所谓VD-MLI指的是在绝热材料的低温区减小层密度，在高温区增大层密度，使得在相同的层数下绝热能力更强。贮箱内低温液体受热蒸发后，其温度与室温仍相差较大，NASA通过在VD-MLI中布置气冷屏结构，回收低温气体的冷量，使得贮箱液体蒸发量进一步降低[2]，这样就形成了SOFI+VDMLI+气冷屏的复合绝热结构，简称为气冷屏复合绝热结构。

目前，对于VD-MLI和气冷屏，国内外已经有研究者分别对其进行研究，但尚未有将两者有机结合起来的研究。Mclntosh[3]提出了逐层传热模型来预测MLI材料的导热性能。Hastings等[4]验证了逐层传热模型在模拟VD-MLI性能时误差小于6%。王田刚等[5]研究了SOFI/VD-MLI的传热特性及最佳层密度，但未涉及气冷屏的研究。赵拓等[6]研究了气冷屏屏位对漏热量的影响，但计算中使用固定的VD-MLI导热系数，不能反映VD-MLI结构的导热系数随冷屏位置变化时漏热量的变化规律。

为此，本文根据低温贮箱在轨阶段的热环境特点，利用气冷屏复合绝热结构的特点，考虑多层变密度的导热系数随冷屏位置的变化因素，以50 L低温贮箱为例对复合绝热结构进行综合优化设计，研究冷屏位置和多层变密度结构的相互影响规律，分析VD-MLI的最佳层密度与气冷屏的最佳屏位。最后与无气冷屏的变密度复合物绝热结构进行对比。

1 气冷屏复合绝热结构

气冷屏复合绝热结构如图1所示，VD-MLI层由交替布置的辐射屏和间隔层组成，又被气冷屏分隔为内外两个部分。气冷屏由蒸气管及冷屏组成，贮箱内部蒸发出的气体的温度比外界温度低，因此当气体在蒸气管中流动时，可以将携带的冷量传递给冷屏，回收一部分冷量，实现减少漏热的效果。结构的最内侧是SOFI层，由于空间飞行器推进剂低温贮箱主要用于太空环境，所以在地面时往往对其绝热结构进行抽气处理，剧烈的气体对流使得地面阶段VD-MLI层隔热性能不足，而SOFI层可以大幅减少地面阶段的漏热量。

图1 气冷屏复合绝热示意图Fig.1 The VCS composite insulation structure

2 数学模型

大型运载火箭低温推进剂贮箱的发射阶段时长远远小于在轨阶段。因此，本文主要针对在轨阶段进行绝热结构设计分析，该阶段贮箱的传热形式包括热传导、热对流以及热辐射等方式。

2.1 气冷屏复合绝热模型

为简化计算，忽略气冷屏本身作为辐射屏的作用并做了假设：（1）不考虑支撑杆与颈管材料导热系数随温度的变化；（2）气冷屏复合结构各部分无接触热阻；（3）冷蒸气的冷量全部用于冷却气冷屏；（4）气冷屏各部分温度相同；（5）气冷屏与相邻的VD-MLI表面间用铜带形成热桥，二者温度近似相等。

根据能量守恒原则，有：

式中：Q1为外界漏入到气冷屏上的热量，W；Q2为冷屏吸收的热量，W；Q3为最终进入到低温贮箱内的热量，W。其中Q1和Q3又可以分为由支撑杆漏入的热量和由VD-MLI结构漏入的热量两部分，如果用VD-MLI结构的表观导热率代表其内部复杂的热传递，则Q1、Q2、Q3可分别表示为：

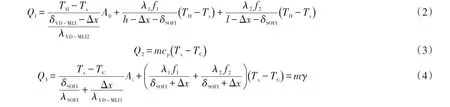
式中：m为贮箱内单位时间低温介质蒸发量（单位时间低温气体产生量），kg/s；cp为低温气体定压比热容，J/（kg·K）；TC为冷边界温度，K；TH为热边界温度，K；Tx为气冷屏温度，K；δVD-MLI为VD-MLI厚度，mm；Δx为气冷屏距SOFI外表面距离，即屏位，mm；λVD-MLI1为冷屏内侧VD-MLI表观导热系数，W/（m·K）；λVD-MLI2为冷屏外侧VD-MLI表观导热系数，W/（m·K）；A0为气冷屏以外绝热层平均表面积，m2；λ1为颈管导热系数，W/（m·K）；λ2为拉杆导热系数，W/（m·K）；f1为颈管横截面积，m2；f2为拉杆横截面积，m2；h为颈管长度，mm；l为支撑杆长度，mm；δSOFI为 SOFI厚度，mm；λSOFI为SOFI导热系数，W（/m·K）；Ai为气冷屏以内绝热层平均表面积，m2；γ为贮箱内低温介质气化潜热，J/kg。

由于：

由此可得:

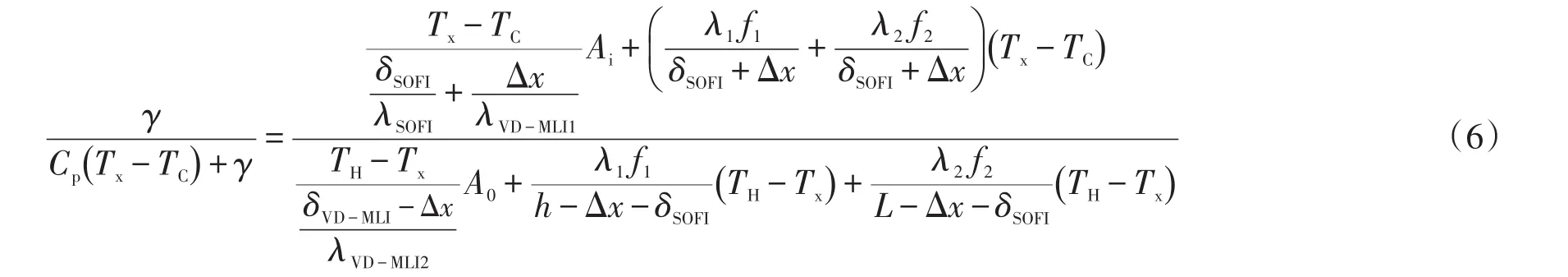
式中：未知参数为λVD-MLI和Tx。其中λVD-MLI会随着冷端温度、热端温度、层密度和层数的变化而变化，只要确定λVD-MLI的大小，就可以解出屏温Tx并反推漏热量。

2.2 泡沫层+多层变密度绝热模型

对于泡沫层+多层变密度绝热结构，常用的分析模型包括逐层传热模型以及Lockheed模型。本文选取逐层传热模型，该模型主要考虑了三种形式的热交换：相邻层之间的辐射换热、相邻层之间的剩余气体导热以及相邻层之间经间隔物进行的固体导热。由于储罐在太空中处于真空状态，气体导热可忽略不计，所以每层总的热流可表示为：

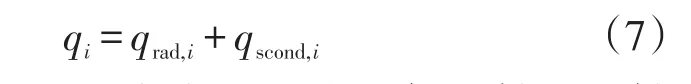
式中：qi为每层总热流密度；qrad，i为相邻辐射层辐射换热热流密度，W/m2；qscond，i为间隔层导热热流密度，W/m2。

辐射层换热热流密度为：

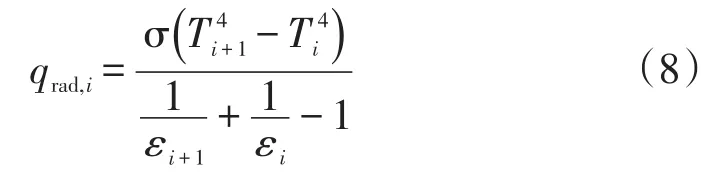
式中：玻耳兹曼常数σ=5.67×10-8W/（m2·K4）；Ti+1和Ti分别是两辐射层表面温度，K；εi+1和εi分别为两表面的发射率，对于双面镀铝聚酯薄膜，取值为0.03。

间隔层导热热流密度为：

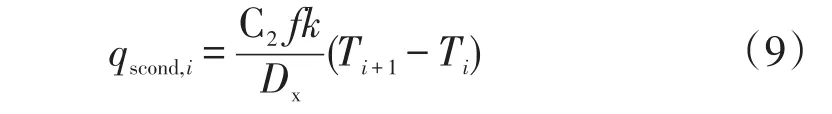
式中：C2为经验常数；f为间隔材料与固体材料的相对密度；Dx为辐射层间的实际厚度，由于辐射层密度不同，所取的值也不同，单位为m；k为间隔材料的导热系数；Ti+1和Ti分别是两辐射层表面温度，K。

在得出热流密度q后，可以计算出VD-MLI在特定温度、层数和层密度下的表观导热系数：

3 仿真计算与分析

由式（6）～（10），可以通过反复迭代解出冷屏温度Tx、VD-MLI温度分布Ti、漏热量Q及VD-MLI的两个表观导热系数λVD-MLI1、λVD-MLI2。式中已知量取值如表1所列。

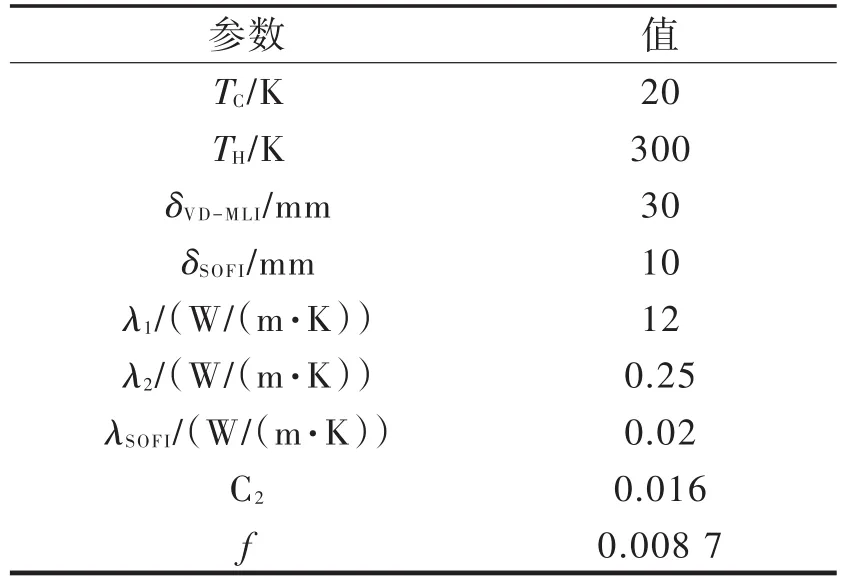
表1 参数取值Tab.1 Value of important parameters

根据逐层传热模型，采用迭代法对多层绝热结构漏热量进行计算。首先沿绝热层厚度方向假定一个线性的温度分布，然后求解相邻两辐射层之间的热流，再通过求得的热流计算出新的温度分布，完成一个迭代周期。该过程一直进行到前后两次温度分布满足收敛条件，即可解出温度分布，并推导出VD-MLI的表观导热率。

在求解冷屏温度时，同样采取迭代法。将VD-MLI分成冷屏内和冷屏外两部分，先假定其表观导热率与无冷屏时相同，然后求解屏温，再用该屏温分别计算内外两部分VD-MLI的表观导热率。一直迭代到前后两次屏温之差满足收敛条件。两种迭代的程序流程图如图2。

图2 求解冷屏温度的两种迭代程序流程图Fig.2 Two kinds of iteration program flow charts for solving cold shield temperature

采用Matlab对气冷屏复合绝热结构和不带冷屏的SOFI/VD-MLI绝热结构进行仿真，贮箱容积为50 L，仿真的冷热边界分别为20 K和300 K。考虑到本文所涉及的项目对绝热结构厚度与重量的要求，选择VD-MLI总厚度为30 mm，总层数为30层，绝热材料为双面镀铝聚酯薄膜和涤纶丝网。

3.1 气冷屏复合绝热的最优层密度

将VD-MLI绝热结构分为等厚度的三部分，n1、n2、n3分别为由内到外每个部分所含的绝热层层数，把VD-MLI划分为三个不同的层密度区，由于每层厚度都为1 cm，因此n1、n2、n3即是层数，也是层密度（层/cm）。由于总层数30层已确定，只用n1和n2就能表示一种层密度组合。其中n1层数最少为5层，最多为10层，n1代表低密度区，n2代表中密度区，n2大于n1。

先在无冷屏的情况下对不同层密度组合下的漏热量进行数值计算，结果如图3所示。可以看出当n1、n2、n3分别为5层、10层、15层时，漏热量最小，为0.593 625 W。这与朱浩唯等[7]提出的低、中、高三个密度区层密度比值为1/2、1、3/2的理论相符合。

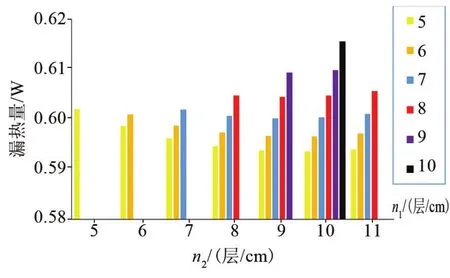
图3 无冷屏时不同层密度组合对应的漏热量Fig.3 Heat leakage of different level density without VCS

再对气冷屏复合绝热结构的不同层密度组合的漏热量进行数值计算。依据赵拓等[6]的研究，当冷屏位于VD-MLI结构的中央，即冷屏将VD-MLI结构从厚度方向等分成两部分时漏热量最小，因此，在所有层密度组合中将冷屏置于距VD-MLI结构内表面15 mm处。计算结果如图4所示。

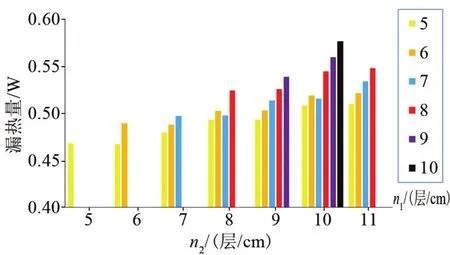
图4 气冷屏复合绝热结构不同层密度组合对应的漏热量Fig.4 Heat leakage of VCS composite insulation structure of different level density

由图4可见，在不同层密度组合下气冷屏复合绝热的漏热量与无气冷屏时相比均有下降。当n1、n2、n3分别为5层、6层、19层时，漏热量最小，为0.466 842 W。此时的最优层密度与无冷屏时的差别很大。因为无冷屏时，对于固定的冷、热端温度，漏热量只由VD-MLI结构的热阻决定。对于气冷屏复合绝热结构，实际进入贮箱的热量Q3是由漏入冷屏的热量Q1与冷屏吸收的热量Q2两部分共同决定的，只要适当地减少冷屏内侧VD-MLI结构的层数，增加外侧的层数，让Q3的减少量大于Q2的减少量，就可以进一步减少漏热量。

3.2 气冷屏的最佳屏位

在原有仿真基础上，再次尝试改变气冷屏的位置，寻找每组层密度组合对应的最小漏热量，计算结果如图5所示，图6与图7为不同层密度组合漏热量最小时气冷屏的位置与屏温，与图5相对应。

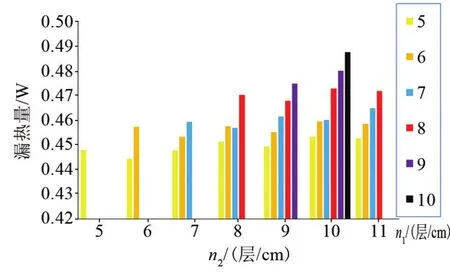
图5 气冷屏复合绝热结构屏位最佳时不同层密度组合对应的漏热量Fig.5 Heat leakage of VCS composite insulation structure of different level density when the VCS is in best position

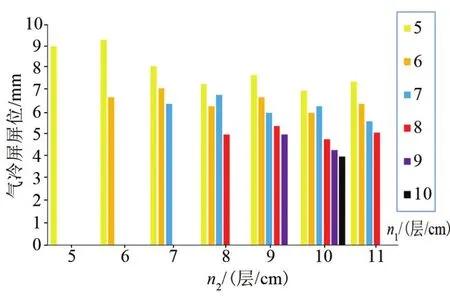
图6 不同层密度组合对应的最佳屏位Fig.6 Best position of VCS of different level density combinations

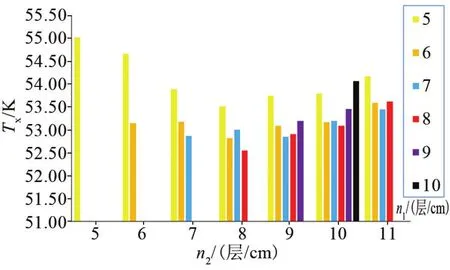
图7 不同层密度组合处于最佳屏位时对应的冷屏温度Fig.7 Txof diffrerent level density combinations when the VCS is in best position）

由图5可见，在各种层密度条件下，均存在最佳屏位，其漏热量较图4进一步减少。对比图4和图5可以发现，最佳层密度是5层/cm、6层/cm、19层/cm，对应最佳屏位距VD-MLI内侧9.3 mm，对应漏热量为0.444 277 W。调整气冷屏屏位后，各层密度组合对应的漏热量都有所下降，并且各层密度组合间的优劣整体上无太大变化。另外，从图6可以看到随着冷屏内侧n1层数的减少，最佳屏位逐渐增大。由图7可以发现冷屏处在最佳位置时，冷屏温度整体接近，都在53 K左右，由于冷屏温度直接关系到冷蒸气所能提供的冷量，也就是气冷屏吸收的冷量Q2。当冷屏温度接近53 K时，若继续减少内侧VDMLI结构的层密度，会导致Q2的减小量大于Q1的减小量，导致漏热量Q1上升。