正交Gaussian-Krawtchouk不变矩的构建及在图像匹配中的应用研究

刘 欢，肖根福，熊 勇

正交Gaussian-Krawtchouk不变矩的构建及在图像匹配中的应用研究

刘 欢1,2，*肖根福3，熊 勇3

(1. 井冈山大学电子与信息工程学院，江西，吉安 343009；2. 江西省农作物生长物联网技术工程实验室，江西，吉安 343009；3. 井冈山大学机电学院，江西，吉安 343009)

针对基于几何矩及不变矩的图像特征描述存在信息冗余，计算复杂，图像表征能力不强等问题，本文深入研究了正交的Gaussian-Krawtchouk矩及其不变矩的表达形式。依据不同的尺度因子特点，提出了基于多尺度Gaussian-Krawtchouk不变矩的图像局部特征描述方法，并用于五种不同类型图像的特征匹配。实验结果表明，这种不变矩较其他传统的特征描述方法具有更好的图像表征能力，更强的数字稳健性。该不变矩用于图像匹配是有效可行的，具有良好的实用价值。

正交Gaussian-Krawtchouk矩；不变矩；GKM描述子；图像局部特征描述

0 引言

图像匹配一直是图像处理研究领域的热点[1-3]。现有图像匹配技术大致可分为基于区域的匹配技术和基于特征的匹配技术，其中后者具有更强的鲁棒性和灵活性。近年来其在图像处理方面得到了广泛的采用与研究，备受关注。图像局部特征描述是基于特征的匹配技术难度最大且最关键的步骤，其描述方法的好坏直接决定了匹配的质量。矩与不变矩的方法由于形式简单，计算速度相对较快，已被证明是图像局部特征描述的一种非常实用的工具[4-6]。几何矩及不变矩最早在1962年由Hu[7]提出7个著名的几何不变矩，此后该矩在图像处理与模式识别中得到了广泛的应用。文献[8]则用几何矩构建非降维模型用于图像分割。文献[9]针对光照与模糊图像，在Hu不变矩的基础上重新构建了新的组合不变矩，但该新组合不变矩只具有较好的光照鲁棒性和模糊不变性，对其他类型因素的影响没有考虑。文献[10]提出用三维几何矩解决高光谱图像分类。张朝鑫[11]将高斯核函数引入几何矩中，重新定义了高斯几何矩及其位移和旋转不变矩并证明了高斯几何矩比几何矩具有更强的特征表述能力和抗噪声干扰能力。文献[12]也提出了一种新的高斯多尺度组合几何矩，将该组合矩与图像的灰度共生矩阵相融合构成新的图像局部特征描述子用于图像的特征点初匹配。

由于几何矩不是正交矩，用其表征图像特征存在信息冗余。于是Teague[13]提出了在连续空间上具有正交性的Legendre和Zernike矩。Zernike矩被认为具有很强的特征描述能力[14-15]。文献[16]利用Zernike提取图像的全局特征，并采用PCA进行降维，用于人脸图像识别。文献[17]则提出一种改进的Zernike矩，利用小尺寸奇数模板求解Zernike矩进行二级定位，获取亚像素级边缘点实现图像边缘检测的精定位。但Zernike矩中采用的是阶乘运算，其运算耗时大，难以满足实时性要求，此外高阶的Zernike矩数字稳定性较差。张朝鑫[18]将Gaussian-Hermite推广到极坐标复数空间，提出了极坐标下的Gaussian-Hermite，并给出了其旋转不变矩的构造方法[19]。此后他又提出多尺度的Gaussian- Hermite矩描述图像特征并用于图像匹配[20]。但以上这些矩皆定义在连续空间上，用于表征数字图像时需要进行数字离散化，必然会导致离散误差，影响矩的计算精度。为了克服连续矩的缺陷，Yap[21]等提出了离散正交的Krawtchouk矩。Krawtchouk矩能够用于提取图像的局部特征，不需要进行近似计算，不存在信息冗余。离散正交矩简单、实用、高效逐渐得到广大图像处理研究学者的重视。Gaussian-Krawtchouk属于正交矩的一种，具有较强的图像特征表征能力且计算简单。但到目前为止，还未有文献采用Gaussian-Krawtchouk矩用于图像匹配方面的研究。

本文提出一种正交Gaussian-Krawtchouk(GK)矩的特征描述方法，首次给出了Gaussian- Krawtchouk矩的定义，探讨了GK的离散形式及计算方法，进而创新性地推演出GK不变矩的表达形式。在此基础上提出多尺度Gaussian-Krawtchouk不变矩的图像局部特征描述方法，并用于图像匹配。最后通过仿真实验，与SIFT和经典Hu几何不变矩进行比较分析。结果表明，GK不变矩的描述子具有更强的图像特征表征能力，低阶矩对噪声不敏感，GK不变矩自带尺度因子，其可控性更灵活，计算简单，实用性更强。

1 GK矩及其不变矩理论

1.1 GK矩

根据Krawtchouk矩的一般定义[21]，提出一种新的矩：Gaussian-Krawtchouk矩，同时构建其不变矩。

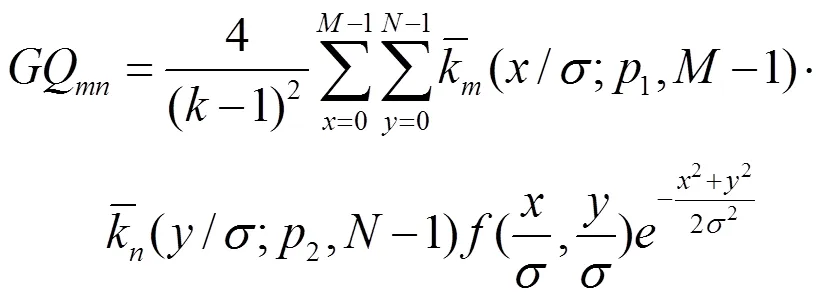
Krawtchouk多项式定义为

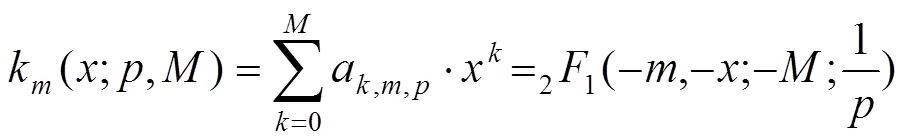
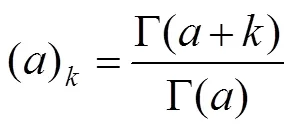
Krawtchouk多项式过零点分布，中间稀疏，边缘较密，满足正交性

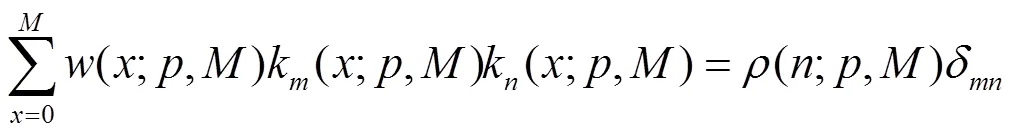
定义规则化后的Krawtchouk多项式为

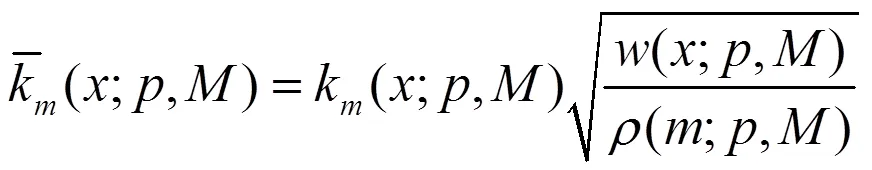
那么最终Krawtchouk多项式如式（1）所示。

1.2 Gaussian-Krawtchouk矩的不变矩

把GK矩表示成高斯几何矩的线性组合，然后通过高斯几何矩的不变矩来构造GK矩的不变矩。高斯几何矩的平移，旋转，尺度不变矩可写成：

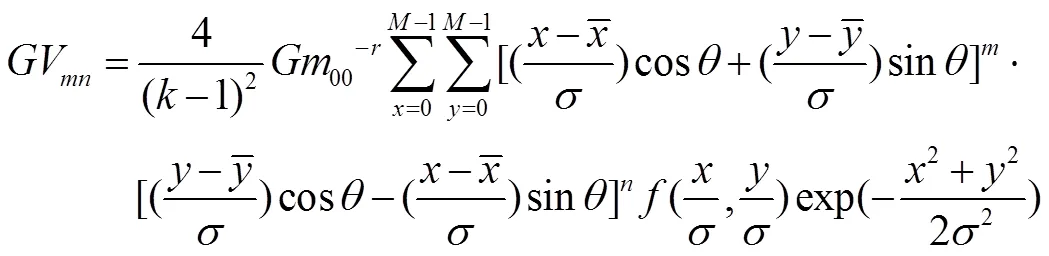
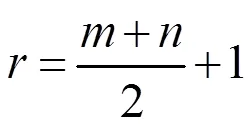
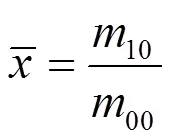
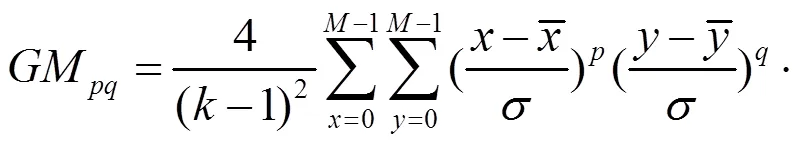
在离散情况下，高斯几何矩的不变矩可重新写成如下：

GK矩的平移，旋转，尺度不变矩则可由下式推出得到：

2 多尺度GK不变矩的图像特征描述方法

下面给出2阶-5阶GK不变矩的形式，共18个。

GKM描述子的具体构造过程如下：

2)计算前5阶共18个GK不变矩；

3)构造18×7＝126维的特征向量

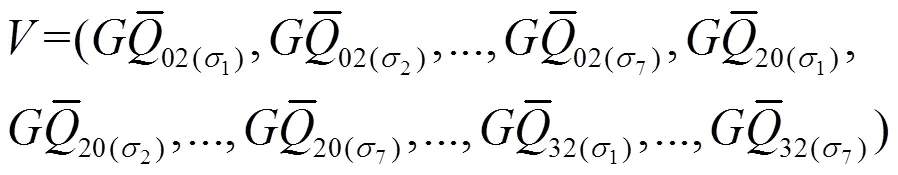
且GKM描述子计算得到的特征向量之后，用欧氏距离进行特征点之间的比较得到正确的匹配对。欧式距离公式为

3 实验

本实验对比了5种状态下GKM描述子的性能。图像来自牛津大学标准图片库。如图1-图5所示。分别是模糊、缩放、光照、视角变换、旋转图像。

图1是模糊图像，图像的模糊度来自相机聚焦的不同，模糊程度依次加剧如图1(a)-(d)。

图2是缩放变化图像，尺度图2(a)-(d)依次变小。

图3是不同光照条件下拍摄的图片，图3(a)-(d)亮度依次变暗。

图4是对同一场景不同视角拍摄的图像，图4(a)-(d)视角依次变大。

图5是是一组经过旋转的图像，图5(a)-(d)旋转角度依次变大。

图1 不同模糊变化图

图2 不同缩放程度图

图3 不同光照变化图

图4 不同视角变化图

图5 不同旋转变化图

本实验分两部分进行，第一部分评估本文所构造GKM特征描述子表征能力。第二部分是特征匹配实验，本文选择经典的特征匹配算法SIFT，SIFT特征检测+高斯几何不变矩，SIFT特征检测+GKM，SIFT+Zernike矩和SIFT+复数矩（CF）作比较。本文所采用的验证算法皆采用SIFT检测特征点，再分别计算SIFT128维特征向量，选择7个不同尺度因子分别计算Hu的7个几何矩（49维）和18个GKM（126维）。实验环境：处理器：Intel(R) Core(TM)i7-6900K，内存：64.0 GB，系统类型：64位操作系统。Window10操作系统，MatlabR2014b+opencv3.4+VS2017。

3.1 GKM特征描述子评估实验

表1 不同模糊程度的18个GKM值

Table 1 The values of GKM with different blur degrees

模糊图1GQ02GQ20GQ11GQ03GQ30GQ12GQ21GQ04GQ40 (a)6.301531.000137.88979-2.22302-1.54090-1.80598-7.427228.168352.43956 (b)6.301821.000087.88914-2.22501-1.53775-1.79527-7.422218.177122.43946 (c)6.302301.000157.89372-2.23017-1.55287-1.80259-7.430128.168332.44060 (d)6.301201.000117.88749-2.22292-1.54083-1.80571-7.418408.170092.42818 平均误差0.000410.000530.002290.002950.003430.004320.004520.003620.00508 平均偏差(%)0.007400.002980.033470.152750.137280.276750.070180.051160.24084 模糊图1GQ13GQ31GQ22GQ05GQ50GQ14GQ41GQ23GQ32 (a)6.748939.997393.30247-2.31271-2.76249-1.99937-4.27440-1.18792-4.96219 (b)6.7500210.002623.29968-2.31139-2.76134-2.00111-4.27342-1.19001-4.96219 (c)6.7398510.011233.30173-2.29419-2.76239-2.00114-4.27513-1.18899-4.96223 (d)6.7601010.001303.30177-2.30997-2.76155-2.00114-4.27441-1.18002-4.97011 平均误差0.007180.005060.001040.007500.000500.000770.000610.003950.00343 平均偏差(%)0.122730.058330.036470.375190.021080.043990.0164230.384020.07964 总平均误差0.00369

表2 不同缩放程度的18个GKM值

Table 2 The values of GKM with different scales

尺度图2GQ02GQ20GQ11GQ03GQ30GQ12GQ21GQ04GQ40 (a)5.258038.903503.92332-2.98757-1.59325-3.31499-8.797507.828382.46907 (b)5.258028.904023.92362-3.00014-1.59332-3.31492-8.798207.818902.46919 (c)5.260028.899273.92276-3.00010-1.58979-3.31528-8.797497.825342.46887 (d)5.258108.903683.92817-3.00010-1.59312-3.31484-8.798027.900112.46894 平均误差0.000860.001940.002160.005430.001490.000170.000310.007000.00012 平均偏差(%)0.018740.025180.063550.209270.108140.005780.004120.034270.00584 尺度图2GQ13GQ31GQ22GQ05GQ50GQ14GQ41GQ23GQ32 (a)4.554462.022858.67291-8.17744-7.17564-4.88576-2.09378-5.19710-5.88239 (b)4.552212.022868.66986-8.17763-7.16987-4.87954-2.11023-5.19720-5.88246 (c)4.553902.023188.67607-8.17835-7.17741-4.88594-2.10274-5.18976-5.88292 (d)4.561202.022788.66988-8.17769-7.17524-4.88658-2.09296-5.19730-5.89102 平均误差0.003430.000160.002570.000340.002820.002720.007080.003230.00366 平均偏差(%)0.086830.008830.034170.004850.045340.067470.389200.071620.07174 总平均误差0.00253

表3 不同光照变化的18个GKM值

Table 3 The values of GKM with different light variations

尺度图2GQ02GQ20GQ11GQ03GQ30GQ12GQ21GQ04GQ40 (a)1.972031.167322.22065-3.37670-1.18614-4.38644-1.666994.838252.71619 (b)1.971231.167352.21879-3.37595-1.18670-4.38883-1.678094.838652.71724 (c)1.971301.171202.21887-3.38122-1.18702-4.38791-1.676814.837972.71328 (d)1.971651.173352.21943-3.38003-1.18720-4.37822-1.668054.838242.71811 平均误差0.000410.002580.000740.002150.000400.004200.005000.000240.00182 平均偏差(%)0.019000.255100.038690.075420.039200.110690.345180.005790.07739 尺度图2GQ13GQ31GQ22GQ05GQ50GQ14GQ41GQ23GQ32 (a)1.487533.511542.78767-1.17605-7.21625-4.38043-7.52842-2.96151-1.44470 (b)1.481513.513432.78732-1.17606-7.21381-4.37633-7.53231-2.96229-1.44382 (c)1.483913.521582.78719-1.17715-7.21358-4.38324-7.52844-2.96139-1.44379 (d)1.481323.512562.78770-1.17602-7.21467-4.38132-7.53111-2.96067-1.44471 平均误差0.002500.003980.000220.000480.001050.002520.001690.000580.00045 平均偏差(%)0.195000.130890.009120.047060.016770.066500.025980.022400.03599 总平均误差0.00253

表4 不同视角变化的18个GKM值

Table 4 The values of GKM with different viewpoints

尺度图2GQ02GQ20GQ11GQ03GQ30GQ12GQ21GQ04GQ40 (a)4.776963.157231.75120-4.23824-4.82103-4.39426-1.267411.765041.68756 (b)4.777253.157151.75093-4.23766-4.82121-4.39254-1.266361.764151.68722 (c)4.775393.156541.74613-4.23727-4.82202-4.39331-1.267231.764661.68708 (d)4.777273.156311.74519-4.23816-4.82311-4.39567-1.268301.766121.66916 平均误差0.000780.000390.002720.000390.000820.001170.000690.000720.00085 平均偏差(%)0.018760.014340.179940.010720.019670.030680.062760.047330.05680 尺度图2GQ13GQ31GQ22GQ05GQ50GQ14GQ41GQ23GQ32 (a)6.799312.951241.54618-1.41268-1.75365-2.08111-3.58358-1.93702-1.27451 (b)6.799332.952411.54655-1.41379-1.75238-2.07547-3.58429-1.92654-1.27385 (c)6.796412.952231.54584-1.40576-1.76336-2.08038-3.59055-1.93215-1.27502 (d)6.799242.952271.54679-1.41274-1.74732-2.07735-3.58702-1.92703-1.27521 平均误差0.000380.000470.000360.003200.005810.002280.002740.004270.00053 平均偏差(%)0.021210.018200.026980.261500.382210.126760.088180.255180.04772 总平均误差0.00253

表5 不同旋转变化的18个GKM值

Table 5 The values of GKM with different rotation changes

尺度图2GQ02GQ20GQ11GQ03GQ30GQ12GQ21GQ04GQ40 (a)3.188292.666293.36538-2.71840-6.21675-1.13760-1.106201.790711.25636 (b)3.186242.666853.36300-2.71563-6.22133-1.13823-1.107331.790501.25517 (c)3.187922.670093.36410-2.71205-6.21803-1.13765-1.106591.790531.25628 (d)3.189422.670143.37002-2.71454-6.20998-1.13958-1.107111.788341.25638 平均误差0.001140.001790.002670.002280.004130.000800.000450.000970.00051 平均偏差(%)0.041300.077180.091730.096920.076720.080110.0461000.062780.04670 尺度图2GQ13GQ31GQ22GQ05GQ50GQ14GQ41GQ23GQ32 (a)4.684552.579217.48639-2.63407-2.26717-1.03393-1.25609-2.96507-5.95656 (b)4.680542.576707.48633-2.62423-2.26734-1.02988-1.25597-2.97084-5.97423 (c)4.675632.578597.49112-2.63455-2.26448-1.03309-1.25569-2.97051-5.95689 (d)4.673942.572287.47762-2.64197-2.27112-1.03308-1.25598-2.97022-5.95820 平均误差0.004170.002710.004880.006300.002370.001550.000150.002370.00739 平均偏差(%)0.103010.121510.075210.276360.120390.173200.013580.092230.14319 总平均误差0.00253

3.2 图像匹配实验

本部分实验使用衡量参数：匹配正确率，召回率评估最后的匹配效果，计算耗时用于衡量匹配的效率。其中匹配正确率，召回率由下述公式得到：

图6-图10列出各类型图像不同方法的匹配正确率-召回率的统计数据，各图中每个散点对应于每种类型图像上的某种方法的正确率-召回率对。图6给出了图1(a)-(d)不同模糊情况下五种描述子匹配的正确匹配率-召回率比较，从图中可以看出，本文GKM非常明显地集中在右上角，即匹配效果更好。图7给出图2(a)-(d)不同缩放程度图的五种描述子匹配的正确匹配率-召回率比较，从图中可以看出，Zernike矩的匹配和GKM的匹配效果都很好，其中Zernike更好一些，GKM次之，复数矩的匹配也还不错，以上三种描述子比SIFT和高斯几何矩要优秀。图8给出了图3(a)-(d)不同光照条件图像的五种描述子匹配的正确匹配率-召回率比较，从图中可以看出，SIFT、GKM和Zernike表现基本相当，其他三种表现稍差。图9给出了图4(a)-(d)不同视角拍摄图的五种描述子匹配的正确匹配率-召回率比较，从图中可以看出，GKM表现最为优秀，SIFT次之，Zernike矩表现一般，高斯几何矩和复数矩表现则不太理想。图10给出了图5(a)-(d)旋转角度不同图的五种描述子匹配的正确匹配率-召回率比较，从图中可以看出，GKM依旧表现最为优秀，始终集中在右上角，其次是SIFT，Zernike矩则表现一般，高斯几何矩和复数矩则表现不太理想。总之，本文的GKM方法在处理五类情况的图像时总体效果都不错，匹配正确率皆在80%以上，其中处理光照，缩放，模糊时其稳定性优势明显，其他情况次之。

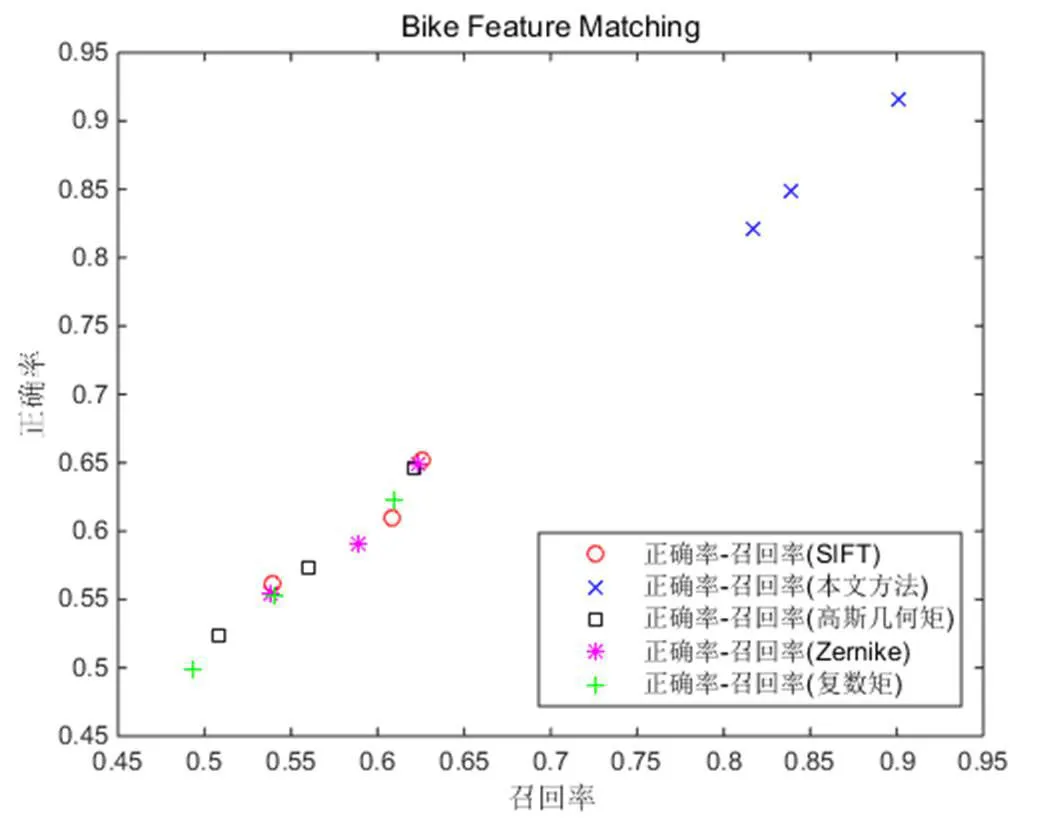
图6 一类图像间的正确匹配率-召回率

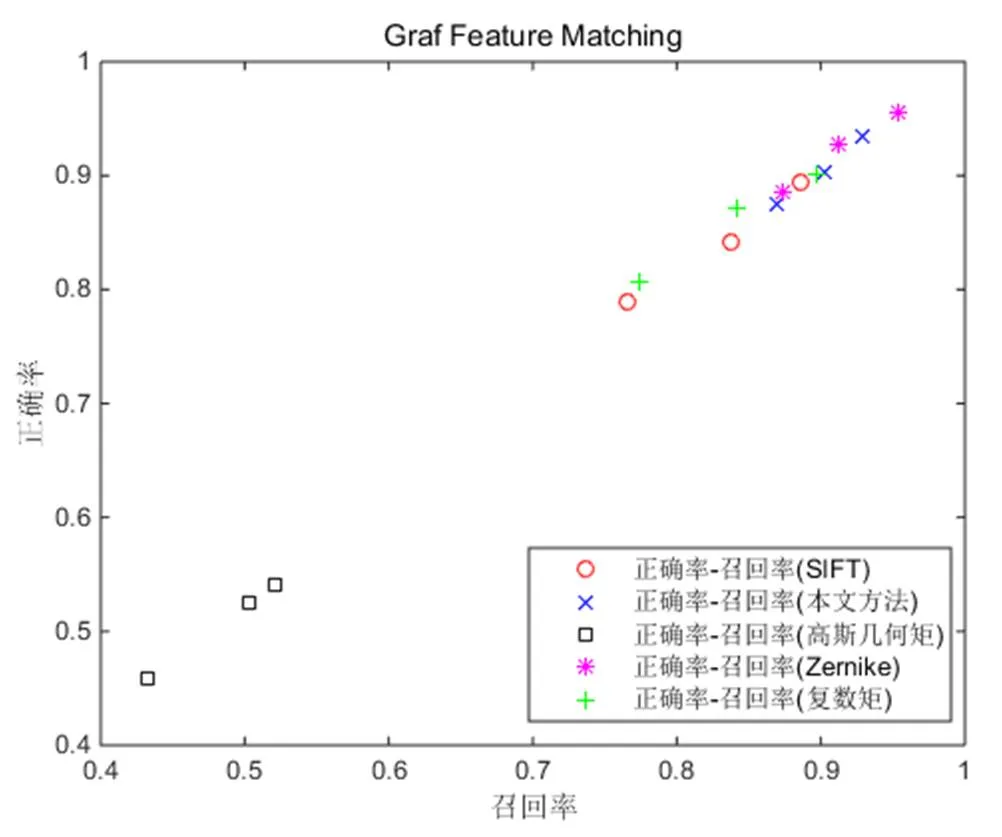
图7 二类图像间的匹配正确率-召回率

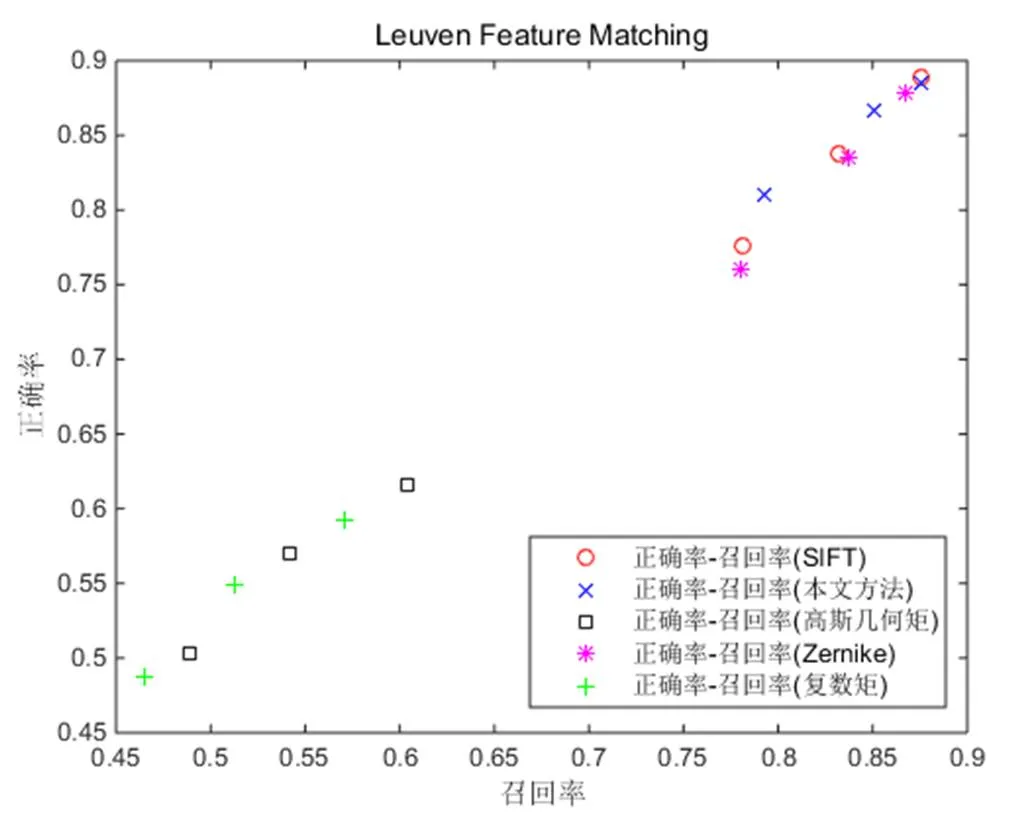
图8 三类图像间的匹配正确率-召回率

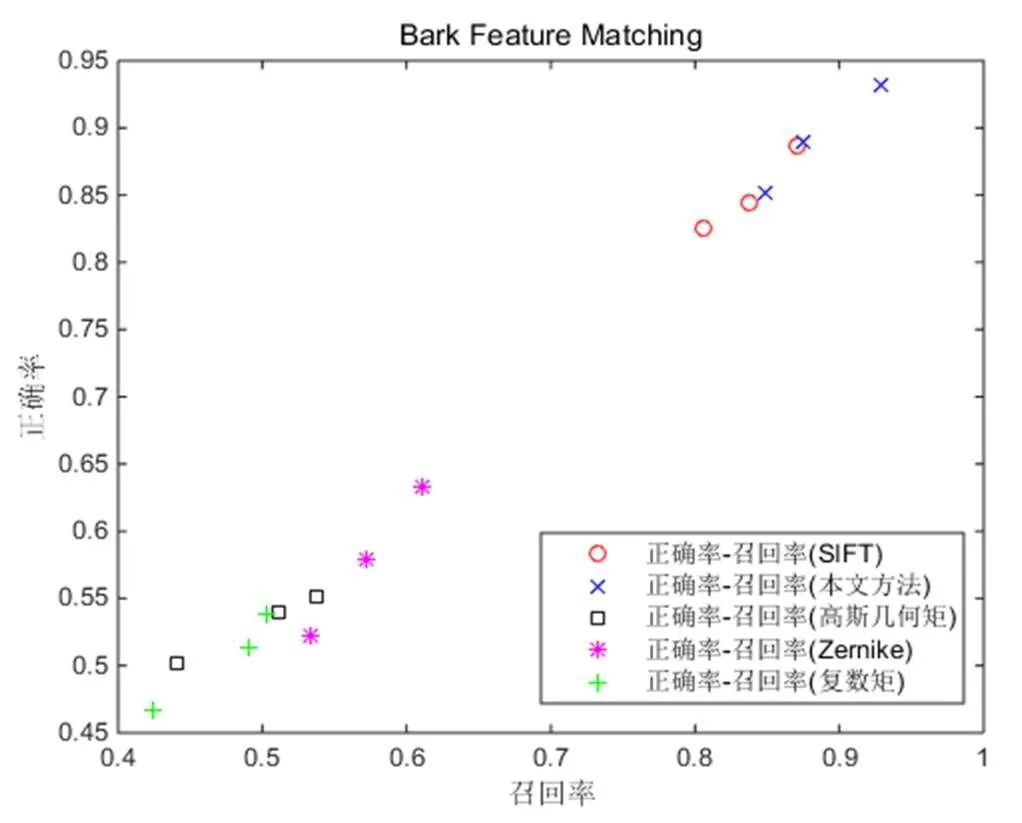
图9 四类图像间的匹配正确率-召回率

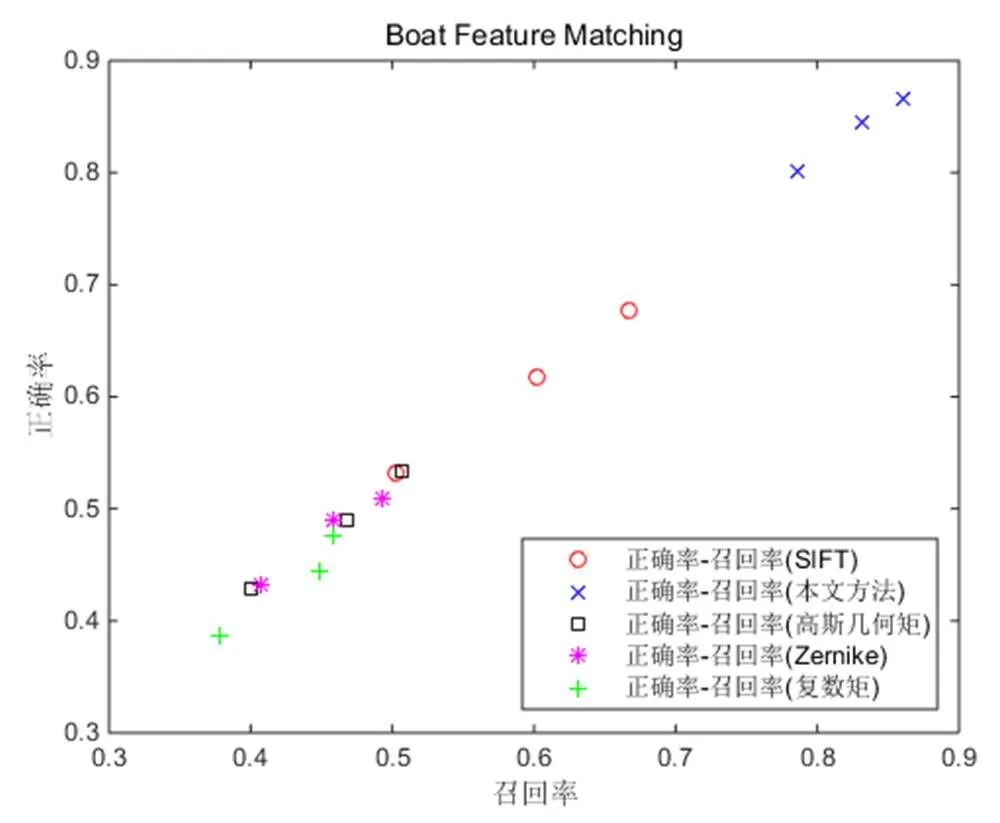
图10 五类图像间的匹配正确率-召回率

表6 几种描述子的耗时比较（s）

Table 6 the comparison of running time between moments

images(a)-(b)(a)-(c)(a)-(d) 高斯几何矩图10.480.330.32 图20.470.440.40 图30.370.350.24 图40.540.420.39 图51.421.311.12 SIFT图11.671.691.73 图21.841.861.92 图31.871.932.05 图41.912.332.39 图54.354.424.54 Gaussian-Krawtchouk Moment(GKM)图11.511.541.43 图21.661.621.68 图31.671.721.76 图41.741.811.83 图53.894.084.31 Zernike图12.882.902.97 图22.271.992.28 图32.042.182.22 图42.172.392.41 图53.545.125.17 复数矩（CF）图14.054.364.42 图23.423.453.63 图33.193.293.31 图43.303.623.78 图55.377.757.83

表6列出了对几种特征描述子计算时间的测试：SIFT描述子、高斯几何矩、Zernike矩、复数矩（CF）、本文的GKM。从表1中数据可知，高斯几何矩耗时最少，其次是GKM，这两种矩描述子所需的计算时间远小于Zernike矩描述子与SIFT描述子。由于复数矩的高阶矩包含了低阶矩致使复数矩计算带来重复计算，冗余性大。因此在上述几种描述子中CF复数矩耗时最长。

4 结论

本文介绍了GKM，给出了GKM的计算方法，详细推导了GKM的平移、旋转、尺度不变矩，提出了基于正交矩GKM不变矩的图像局部特征描述方法并用于不同类型图像的匹配。通过实验与现有的方法的分析比较，实验结果表明：基于GK矩的图像特征描述方法比现有的方法具有更稳定的数字性能，更强的图像表征能力且计算简单，实用性更强。本文没有详细研究GKM的高阶不变矩的推导和应用，下一步将开展这一方面的研究工作。

[1] 陈雪松,陈秀芳,毕波,等. 基于改进SURF的图像匹配算法[J]. 计算机系统应用, 2020, 29(12): 222-227.

[2] 陈国翠,顾桂梅,余晓宁,等. 融合PHOG和BOW-SURF特征的接触网绝缘子缺陷检测方法[J]. 小型微型计算机系统, 2021, 42(1): 172-177.

[3] 曹留霞,王晓红,李闯,等. BRISK-DAISY无人机影像匹配算法研究[J]. 测绘工程, 2020, 29(2): 17-22.

[4] Xiao B, Ma J F, Cui J T. Combined blur, translation, scale and rotation invariant image recognition by Radon and pseudo-Fourier-Mellin transforms[J]. Pattern Recognition, 2012, 45(1): 314-321.

[5] Papakostas G A, Koulouriotis D E, Karakasis E G, et al. Moment based local binary patterns: a novel descriptor for invariant pattern recognition applications[J]. Neurocomputing, 2013, 99: 358-371.

[6] Yang J, Xie S. Fingerprint matching based on extreme learning machine[J]. Neural Computing and Applications, 2013, 22(3/4): 435-445.

[7] Hu M K. Visual pattern recognition by moment invariants[J]. IRE Transactions on Information Theroy, 1962, 8(2): 179-187.

[8] 曹地,曹建农,朱倩. 一种基于图像几何矩的非降维连续尺度解构模式[J]. 遥感信息, 2019, 1(34): 44-50.

[9] 刘欢,郝矿荣,丁永生,等. 光照鲁棒的抗模糊新组合不变矩图像匹配方法[J]. 传感技术学报, 2013, 26(9): 1-7.

[10] Kumar, B. Hyperspectral image classification using three-dimensional geometric moments[J]. IET Image Processing, 2020, 14(10): 2175-2186.

[11] 张朝鑫,席平. 高斯几何矩及其在特征匹配与图像配准中的应用[J]. 计算机辅助设计与图形学学报, 2014, 26(7): 1116-1125.

[12] Xiao G F, Liu H, Ouyang C J, et al. Multifeature fusion and mutual co-operative particle swarm optimization in three-dimensional reconstruction of belly[J]. Journal of Electronic Imaging, 2019, 28(2): 021003-1-021003-14.

[13] Teague M R. Image analysis via the general theory of moments[J]. Optical Society of America, 1980, 70(8): 920-930.

[14] Xia T, Zhu H, Shu H, et al. Image description with generalized pseudo-Zernike moments[J]. JOSA A, 2007, 24(1): 50-59.

[15] Zen C, Shu-Kuo S. A Zernike moment phase-based descriptor for local image representation and matching[J]. Image Processing, IEEE Transactions on, 2010, 19(1): 205-219.

[16] 华珊珊.基于Zernike特征提取和LDA的人脸图像识别方法[J]. 控制工程, 2018, 25(2): 198-203.

[17] 刘明佩,朱维斌,叶树亮. 基于改进Zernike矩的小模数齿轮亚像素边缘检测[J]. 仪器仪表学报,2018,39(8): 259-267.

[18] Shen J. Orthogonal Gaussian-Hermite moments for image characterization[C]. Proc. SPIE, Intelligent Robots and Computer Vision XVI: Algorithms Techniques, Active Vision, and Materials Handling, Pittsburgh, USA, 1997, 875-894.

[19] 张朝鑫,席平,胡毕富. Gaussian-Hermite矩旋转不变矩的构建[J]. 北京航空航天大学学报,2014,40(11): 1602-1608.

[20] 张朝鑫,席平. 基于Gaussian-Hermite矩的图像局部特征描述与匹配研究[J]. 图学学报, 2014, 35(3): 429-434.

[21] Yap P T, Paramesran R, Ong S H. Image analysis by Krawtchouk moments[J]. IEEE Transactions on Image Processing, 2003, 12(11): 1367-1377.

CONSTRUCTION OF INVARIANTS OF ORTHOGONAL GAUSSIAN-KRAWTCHOUK MOMENT AND THE APPLICATION IMAGE MATCHING

LIU Huan1,2,*XIAO Gen-fu3, XIONG Yong3

(1. School of Electronic and Information Engineering, Jinggangshan University, Ji’an, Jiangxi 343009, China; 2. Jiangxi Engineering Laboratory of IoT Technologies for Crop Growth, Ji’an, Jiangxi 343009, China; 3. School of Electromechanical, Ji’an, Jiangxi 343009, China)

Aiming at the problem of information redundancy, complex calculation and low image representation of the method of the image feature description based on the geometric moment and invariant moment, orthogonal Gaussian-Krawtchouk moment and its invariant moment are deeply studied. According to the traits of different scale parameters, a description method on image local features based on multi-scale Gaussian-Krawtchouk invariant moment is presented, and was applied in the tests of image trait matching in five different types of images. The experimental results show that the proposed description method performs much better than the other traditional description methods with better image representation ability and stronger digital stability. The invariant moment applied in image matching is feasible and validate. It can offer a nice reference value.

orthogonal Gaussian-Krawtchouk moment; invariant moment; GKM descriptor; image local feature description

TP391

A

10.3969/j.issn.1674-8085.2021.02.011

1674-8085(2021)02-0061-09

2020-12-09；

2021-01-18

国家自然科学基金项目（61640412, 61762052, 42061055）；江西省自然科学基金项目（20192BAB207021，20202BABL202047）；江西省教育厅科技计划项目(GJJ201008)，江西省高校人文社科项目(YS20129)。

刘 欢(1981-)，女，江西吉安人，副教授，博士，主要从事图形图像处理、机器视觉、模式识别(E-mail:liuhuan816618@163.com);

*肖根福(1980-)，男，江西赣州人，副教授，博士，主要从事智能计算、模式识别(E-mail:xiaogenfu@163.com);

熊 勇(1970-)，男，江西吉安人，实验师，主要从事图像处理、智能优化(E-mail:xiongong@163.com).