月面特征稀疏环境下的视觉惯性SLAM方法

2021-03-27谢洪乐陈卫东范亚娴王景川

航空学报 2021年1期

谢洪乐，陈卫东，范亚娴，王景川

上海交通大学电子信息与电气工程学院自动化系，上海 200240

月面科学探测是一项具有重大科研价值的任务[1-2]，在月球车执行月面探测任务时，首先需要解决的一个关键难题是确定其自身的准确位置，以保证其能够导航至目标位置[3-4]。但是由于月球表面没有全球卫星定位与导航系统，所以月球车很难直接获取其准确的定位信息[3-5]。

目前，现有的月球车主要是依据其所携带的传感器去感知周围的环境信息，结合月球车的运动状态进行定位，常用的定位方式有：航迹推算、无线电测量和星敏观测等定位方法[3]。由于航迹推算存在较大的累计误差，无线电测量和星敏定位等方法的准确度较低，一般只能实现十米级的定位精度，且无线电定位存在信号较弱、星敏定位存在星系的能观性比较差等缺点，导致月球车基于上述方法都难以实现准确的定位[3-4]。

近年来，随着计算机视觉的迅速发展，基于视觉的定位方法逐渐成熟，同时定位与地图构建(Simultaneous Localization and Mapping，SLAM)在许多场景取得了显著的定位效果提升。目前，现有的视觉SLAM方法主要包括直接法[6-7]和间接法[8]。直接法采用像素梯度信息进行连续图像帧之间的数据关联[6]，而间接法采用特征点进行图像帧之间的匹配[8]。由于月面的沙质环境难以提取稳定、鲁棒的视觉特征进行可靠的跟踪定位，且纹理信息较少，存在相似重复的环境特征会影响定位系统的精度和稳定性。基于像素梯度信息的匹配方法效果比较差，所以比较适合采用基于特征点法的视觉SLAM方法。同时，由于月面环境为典型的非结构化环境，不满足曼哈顿世界结构特征假设[9]，不存在较多的直线和平面等结构化信息，因此不能用直线特征，所以本文采用基于稀疏特征点的视觉SLAM方法。

由于月面场景的纹理信息比较少，采用纯视觉的SLAM方法在特征稀疏的场景定位效果比较差，所以考虑增加一些辅助的传感器以提升定位的性能。近年来，基于多传感器融合的方案逐渐取得了更好的定位准确性和鲁棒性，特别是视觉惯性融合定位方法，例如OKVIS[10]、VI-ORB-SLAM[11]和VINS-Mono[12]等方法，将惯性测量单元(Inertial Measurement Unit，IMU)的信息作为短期的连续帧之间运动估计，用于修正视觉定位的误差，取得了更高的定位精度[13]。所以本文主要研究一种视觉惯性融合SLAM方法。

针对月面环境的特征稀疏的特点，在之前工作的基础上[14]，提出一种基于多层光流跟踪的前端帧间数据关联方法，采用四元树结构，依据特征值响应强弱选择有效的特征点进行跟踪，实现了一个高效、鲁棒的前端光流跟踪方法。

针对月球车的相机视野特点，由于月球没有大气层，月球车的相机能够观测到遥远的恒星点，但是恒星点往往处于无穷远点的位置，这对于视觉惯性里程计(Visual-Inertial Odometry, VIO)是无效的观测信息，这些无穷远的路标点会严重影响视觉惯性里程计滑动窗口优化的准确性，进而影响定位的精度。所以针对月球车相机的成像特点，提出了一种恒星点剔除算法，基于局部图像灰度二阶矩进行恒星区域特征判断，通过图像多层金字塔进行尺度优化，能够快速、有效地剔除恒星点，实现了定位性能的进一步提升。

基于位姿图优化的方法，将视觉相机和惯性测量单元的测量信息加入后端因子图优化，最终实现了一个准确、高效的月球车视觉惯性SLAM方法，能够持续地进行高精度的六自由度位姿解算，并且搭建了月球车仿真样机和月面仿真环境，通过在多种不同的仿真月面场景下的测试，仿真结果验证了本文方法的定位准确性和鲁棒性。

1 系统整体框架

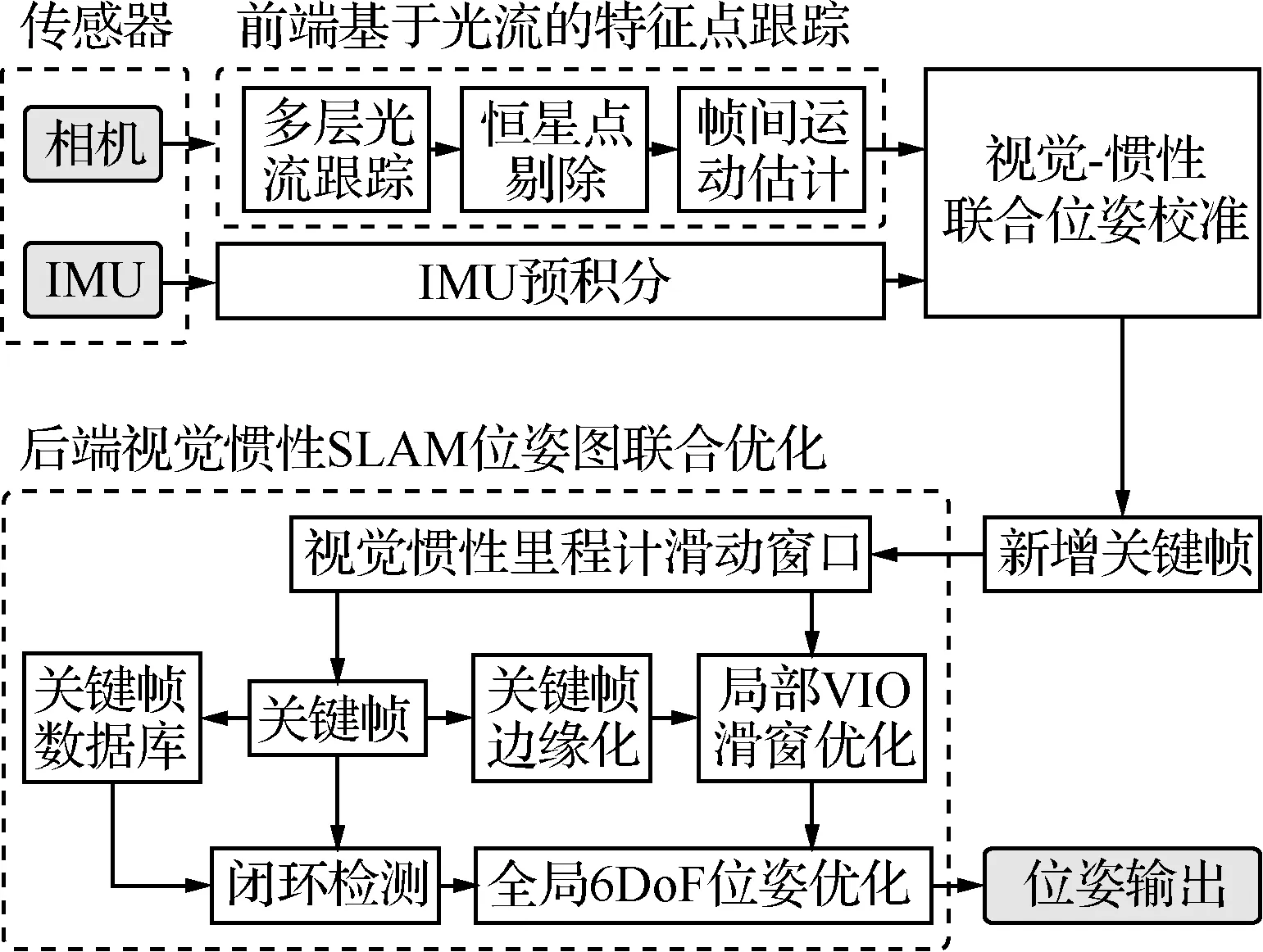
本文的视觉惯性SLAM方法在之前工作[14]的基础上进行改进和优化，由于之前工作主要针对室内无人机定位系统，其俯仰角和滚转角状态是可观测的，所以只进行了位置和偏航角的四自由度(Degree of Freedom, DoF)优化，本文针对月球车的实际传感器特点，在原始四自由度优化的基础上改进，增加了六自由度(6DoF)位姿优化，提升了位姿估计的准确度。并且针对月面环境的特点，提出一种恒星点剔除算法，改善了前端基于光流的数据关联的鲁棒性。本文视觉惯性SLAM系统框架如图1所示，主要包括传感器数据预处理、前端基于光流的特征跟踪和后端视觉惯性SLAM位姿图联合优化等3个部分。

在预处理阶段，惯性测量单元的数据采用IMU预积分的形式[15]，在短期内提供相邻帧之间的相对位姿估计，相机图像采用区域直方图均衡化进行图像增强。然后，相邻图像帧之间采用光流法进行前端数据关联，并且基于四元树进行改进，在多层图像金字塔中选择鲁棒的特征点进行跟踪，采用恒星点剔除算法将无穷远点进行剔除，提升了特征关联的鲁棒性。利用惯性测量数据优化视觉测量的尺度因子，并对齐2个传感器的位姿估计结果，实现视觉惯性联合位姿校准。

在后端视觉惯性SLAM位姿图联合优化部分，基于视觉惯性里程计滑动窗口优化方法，将新增的关键帧依次通过滑动窗口进行优化。并且在全局位姿图四自由度优化方法[14]基础上进行改进，在全局位姿图优化时，联合优化位移、偏航角、俯仰角和滚转角，实现了六自由度的位姿图优化，能够提供鲁棒、高精度的位姿估计。

2 前端基于光流的特征点跟踪方法

2.1 多层光流跟踪方法

视觉惯性SLAM方法的前端图像特征数据关联的准确性，会很大程度地直接影响视觉惯性SLAM方法的整体定位精度。目前现有的视觉惯性SLAM主要是基于特征点匹配和光流2种方法，由于特征匹配方法的实时性一般较差，所以在视觉惯性里程计中，往往使用光流法作为一种轻量化的前端视觉特征数据关联的主要方法。常使用 KLT(Kanade-Lucas-Tomasi)光流跟踪方法[16]，假设相邻的图像之间满足灰度一致性，通过局部像素灰度信息进行匹配，进而拟合出最优的图像特征点的运动状态，并且通过多层图像金字塔结构优化，能够提升光流法在较大视角变化情况下的鲁棒性和准确度[16]。

稀疏光流的效果直接取决于其所跟踪特征点的质量，所以在之前工作的基础上[14]，采用基于四元树的二维平面搜索策略改进多层光流跟踪方法。假设图像金字塔层数为L，在τ时刻的关键帧Kτ中，采用四元树搜索策略筛选光流稳定跟踪的特征点集合φ(Kτ)，依据关键帧图像高斯核尺度的二次幂，正比分配在各层的特征点数，在每一层的图像中采用四元树搜索局部Harris响应值最大的特征点，用于KLT光流跟踪[17]，假设四元树的子节点总数为N，在相邻帧之间光流跟踪过程中，特征点集合φ(Kτ)的迭代公式为

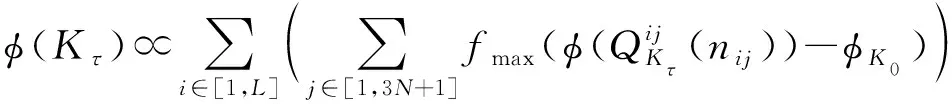
(1)

相比于基于非极大值抑制(Non-Maximum Suppression，NMS)的特征点筛选方法[18]，本文方法在保证特征点均匀分布的同时，也能够有效地选择可以被光流鲁棒跟踪的特征点。为验证本文方法的有效性，进行对比测试如图2所示。

在基于非极大值抑制约束的特征点筛选方法中，采用光流法常用的GFTT(Good Features to Track)特征[19]用于KLT光流跟踪[17]。其中，为保证特征点能够均匀地分布在图像平面，采用像素距离阈值进行约束。假设特征点之间最小距离阈值为Fm，若特征点之间的距离小于阈值Fm时，则依据非极大值抑制方法[18]进行特征选择，保留特征值最大的特征点，最终得到关键帧Kτ的特征点集合φ(Kτ)，采用KLT光流跟踪方法[17]实现相邻关键帧(Kτ和Kτ+1)之间的特征关联。由于光流跟踪往往存在误匹配点，所以采用与VINS-Mono[12]一致的策略，利用基础矩阵模型估计的随机抽样一致性(Random Sample Consensus，RANSAC)方法去除误匹配点，最终得到满足运动一致性的光流跟踪结果。其中，不同方法的光流跟踪测试结果对比，如图2所示。

在光流跟踪性能测试中，关键帧Kτ特征点数均满足|φ(Kτ)|≤300，即提取特征点数量的最大值为300个，像素分辨率为848×480。在基于非极大值抑制方法中，依据像素距离阈值不同，设置了3组对比仿真测试，分别为Fm=10、Fm=20和Fm=30。其中，Fm值越大，对应的特征分布越均匀，但是特征的鲁棒性往往会越差。在本文方法中，保持与非极大值抑制方法一致的特征点数量约束|φ(Kτ)|≤300，并且采用相同基础矩阵约束的RANSAC策略，保持严格控制变量的对比测试，最终的测试结果，如图2所示。

当Fm=10时，光流跟踪的特征点分布比较集中，存在较多特征分布在月面和太空的交界区域，如图2(a1)、图2(b1)和图2(c1)所示，位于交界曲线上的特征点虽然满足GFTT特征值约束，但是此处的特征点沿着交界曲线方向具有较大的不确定性，所以会导致光流跟踪不稳定。而且在快速运动情况下，若特征点分布过于密集时，会存在较多的特征点移出相机的视野范围的情况，此时会导致较大的光流数据关联误差。

当Fm=20和Fm=30时，光流跟踪的特征点分布比较均匀，但由于固定的最小像素距离Fm限制，在纹理显著的区域不能提取大量的特征点，反而在图像模糊的区域提取到一些次优的特征点，所以导致光流跟踪的鲁棒性下降。

本文方法能够在多层图像金字塔中，采用四元树搜索策略检索鲁棒的特征点，优化了光流跟踪策略。特征点光流跟踪成功率比较，如表1所示。本文方法的平均跟踪(Tracking)和RANSAC匹配的成功率分别为94.27%和75.80%，仅略低于非极大值抑制Fm=10方法，但本文方法相对于Fm=10方法，具有更好的特征分布均匀性和鲁棒性。综上所述，本文方法实现了较高的特征跟踪成功率和较好的光流估计的一致性。

在上述测试结果中，基于非极大值抑制方法的前端特征跟踪的平均时间消耗约为19.5 ms/帧，而本文方法的前端特征跟踪的平均时间消耗约为17 ms/帧。所以，本文方法具有更好的实时性，满足计算的实时性需求。

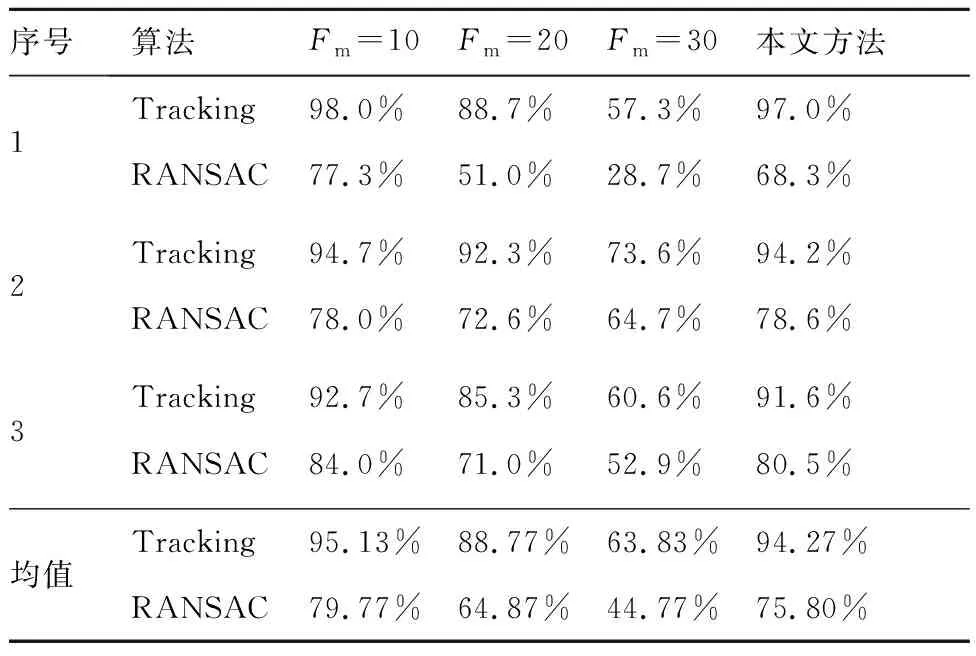
表1 光流跟踪成功率比较Table 1 Comparison of optical flow tracking success rates

2.2 特征点的逆深度估计

特征点逆深度估计是指在视觉SLAM方法中，通过估计特征点深度值的倒数实现其坐标参数化，进而求解特征点三维空间坐标的一种有效方法[20]。设一个特征点在世界坐标系下的齐次坐标位置为Gfk∈R4×1，其中Gfk=[Gxk,Gyk,Gzk,1]T，上标G表示在世界坐标系下。假设在视觉惯性SLAM滑动窗口中，有n个关键帧对该特征点存在有效的观测，记这些关键帧集合为Φ={Kτ},τ=1,2,…,n。在每次观测中，特征点在对应的图像坐标系下的像素坐标为pk=[uk,vk,1]T，设该特征点的深度值为λk，依据相机的投影关系可得

λkpk=Mc[Rk,Tk]Gfk

(2)

式中：Mc∈R3×3为相机传感器的参数矩阵；Pk=[Rk,Tk]∈R3×4为世界坐标系到相机坐标系的投影矩阵，即表示当前关键帧的位姿矩阵。其中Rk∈R3×3为旋转矩阵，Tk∈R3×1为平移向量。依据投影关系可简化为

λkpk=McPkGfk

(3)

(4)

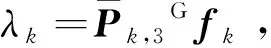
(5)

在特征点三维坐标Gfk的参数化计算过程中，其对应的深度λk估计值的取值范围为(λmin,+∞)，其中λmin为相机有效观测的最小距离。因为无穷大在数值求解过程中存在较大的误差，所以采用1/λk形式进行参数化求解[20]，也称为逆深度计算。所以，式(5)可转化成下面方程进行求解：

(6)

通过连续帧之间特征点的共视观测关系，可求解上述方程。但是月面没有大气层，月球车装载的相机往往可以看到很遥远的恒星，此时恒星特征点位于无穷远点，采用有限值去逼近无穷远点，会导致上述方程式(6)的极大似然估计的解会存在较大的非线性拟合误差。所以提出一种恒星点消除算法，将无穷远的特征点进行剔除，以保证视觉惯性里程计的滑动窗口优化的准确性。

3 恒星特征点剔除算法

由于恒星点往往都是无穷远点，当月球车前进时，无穷远点对于前进方向的位移估计几乎没有作用，仅对于旋转运动会有一些辅助作用，所以对恒星点进行剔除。针对月面环境的特点，在月球车相机所观测的图像中，恒星位置一般为无穷远点，且位于图像的上半部分，恒星所在的像素区域往往处于颜色较深的太空背景区域，而恒星为这一区域的唯一的中心亮点，所以针对月球车图像像素灰度分布特点，提出一种基于局部像素区域的灰度二阶矩方法，能够将恒星特征点进行有效地剔除，提升特征点的鲁棒性。

假设在当前帧图像中光流跟踪的一个特征点坐标为Ak(uk,vk)，计算其所在高斯金字塔图像的区域图像的灰度二阶矩的值来进行恒星点的判断。任取图像上一个像素点Pi(xi,yi)，设这个点所在的图像对应位置像素的灰度函数为I(xi,yi)，通过计算图像局部窗口灰度特征来判断是否为恒星点区域，其中，像素灰度二阶矩的计算公式为

(7)

式中：α为权重；Θ为像素点Ak的邻域；Ω为对应邻域的面积。Θ和Ω的计算公式为

(8)

(9)

式中：γ为选取的邻域半径。计算以特征点坐标(uk,vk)为中心，半径范围在γmin至γmax之间的环形区域Θ的像素灰度二阶矩H值。通过判断图像的像素灰度二阶矩H值是否小于局部灰度阈值来判断是否为恒星点。其中s为尺度因子，在多层光流跟踪时，s与光流跟踪的金字塔层数一致。

恒星特征点剔除方法的测试结果如图3所示，图3(a)为原始的KLT光流跟踪的测试结果[12]，由于恒星点为局部亮点区域，往往是一个易于光流跟踪的特征点，但是由于此特征点一般位于无穷远处，而数值求解该特征的空间位置会导致系统定位性能下降，所以采用恒星点剔除算法，如图3(b)所示，图中红色和蓝色的方块分别为稳定跟踪和新增的光流特征点，白色圆圈的位置为剔除的恒星点区域，通过四元树改进的光流能够更均匀地跟踪鲁棒的特征点，并且通过恒星点剔除算法，能够有效地将恒星点剔除。

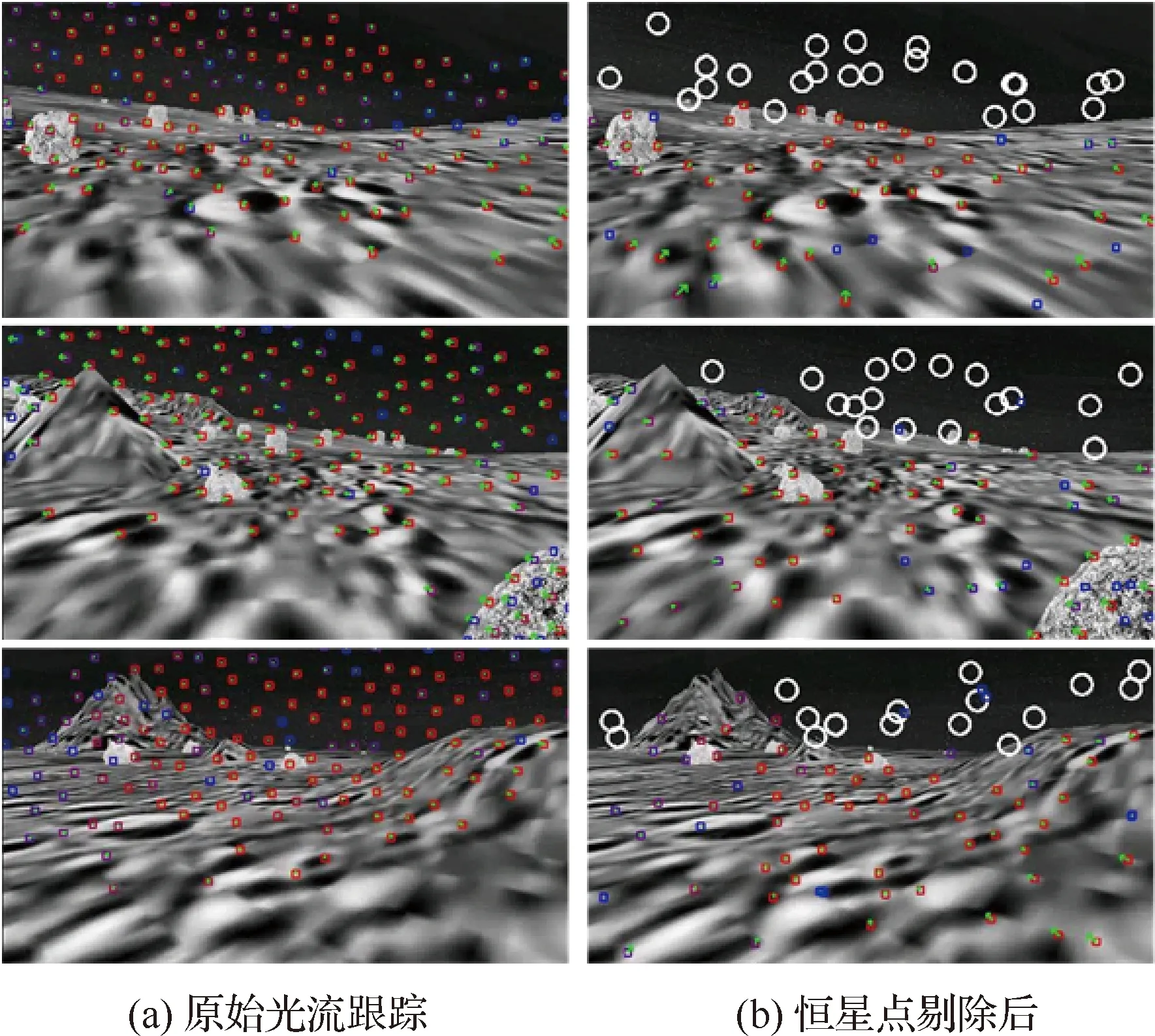
本文提出的恒星点剔除方法只需要在光流稳定跟踪的特征点中增加恒星点判断，所以方法具有较高的实时性，平均每帧图像大约能够稳定光流跟踪100～150个有效特征点，恒星点剔除方法的平均耗时约5～8 ms/帧，满足月球车视觉惯性SLAM方法的计算实时性需求。

4 视觉惯性SLAM位姿图联合优化

在视觉惯性里程计后端优化部分，在VINS-Mono系统[12]的基础之上进行改进和优化，由于视觉惯性里程计往往适用于无人机等平台，配备了高性能的惯性测量单元，其中，飞控系统的俯仰角和滚转角的状态往往是可观的，所以往往只需要进行四自由度的优化，包括位移和偏航角。但是由于月面环境重力加速度值往往不够准确，将4DoF优化改成6DoF优化，包括位移、偏航角、俯仰角和滚转角。在视觉惯性里程计滑动窗口优化中，优化的状态变量Xτ为

(10)

(11)

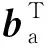
(12)

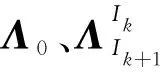
5 仿真验证与分析

针对实际月球车在月面执行科学探测的任务特点，搭建了一个月球车仿真样机和一套模拟月球表面场景的计算机仿真系统，用于验证月球车定位方法的性能。

仿真系统采用开源机器人操作系统(Robot Operating System, ROS)框架下的Gazebo仿真引擎作为开发工具，采用Gazebo-7.4.0机器人仿真平台，使用C++语言在Ubuntu 16.04系统下开发，软件开发平台为Microsoft Visual Studio Code 2019。计算机硬件配置为：CPU处理器为Intel Core i7-7700HQ, 主频为2.80 GHz，计算机内存为8 Gb RAM。使用的机器人操作系统为Ubuntu 16.04 ROS Kinetic。

5.1 月球车仿真样机平台

利用Gazebo仿真引擎搭建的月球车仿真样机平台如图4所示。仿真月球车样机的整体高度为1.046 m，宽度为0.75 m，长度为1.005 m，轮子直径为0.5 m。仿真月球车采用星球车常用的四轮独立驱动结构，利用4个相互独立的电机控制器来分别调节4个车轮的控制力矩，进而控制4个独立车轮运动，通过差速驱动方式实现月球车能够平稳地运动在崎岖的月面。月球车具有较好的越障能力，能够正常行驶在最大倾斜度为25°的斜坡区域，而且能够翻越最大高度约20 cm的陨石、沙堆等障碍物。在仿真平台中，设置可调节的月球车平移速度范围为0.05～3 m/s，角速度范围为0.05～1.5 rad/s，满足实际月球车仿真测试的平移速度与角速度需求。

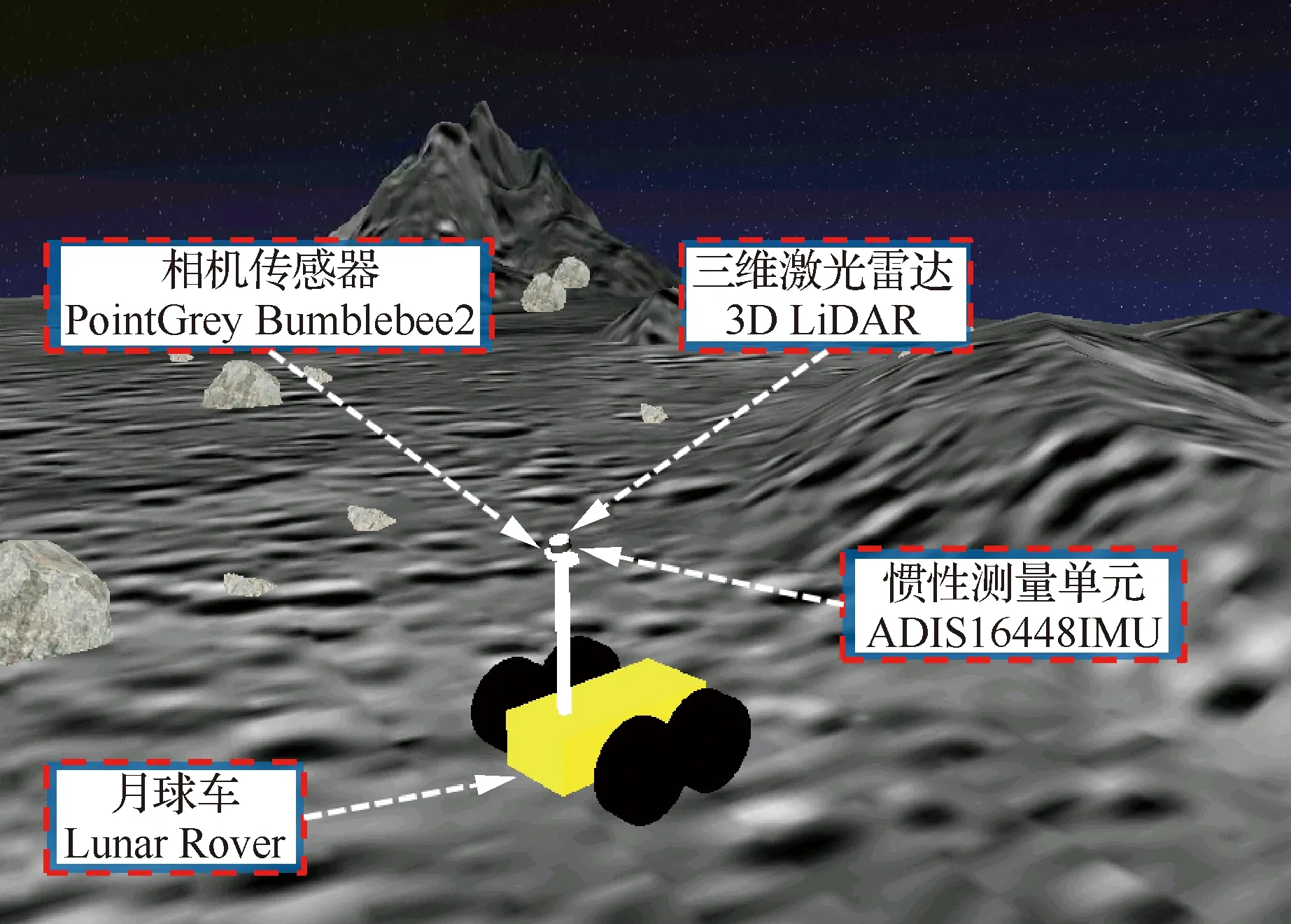
月球车仿真样机平台搭载了多种传感器，能够进行传感器测量数据的仿真，主要传感器包括：双目视觉传感器、三维激光雷达和惯性测量单元。其中，采用的视觉传感器型号为PointGrey Bumblebee2，为了保证实时性和定位性能，在仿真系统中，设置相机的分辨率为848×480，频率为20 Hz。其中，相机安装高度为0.984 m，相机与水平方向的向下倾斜角度为13.5°，仿真测试中采用双目相机的左侧相机的图像数据。IMU位于双目相机的中心位置，IMU型号为ADIS16448，在仿真中设置更新频率为100 Hz。

通过仿真平台可以进行月球表面重力模型的仿真，能够模拟月球表面的重力情况。在月球车仿真平台中，月面重力加速度为1.62 m/s2，约为地球表面重力加速度的1/6。

并且，在仿真月球车平台上，具备定位轨迹真值(Ground Truth)的保存功能，能够实时地记录月球车在移动过程中真实轨迹和位姿。定位轨迹真值与月球车平台上IMU的实时位置一致，能够表征月球车在世界坐标系下的实际移动轨迹，真实轨迹可用于评估不同算法的定位性能。

5.2 月面仿真场景数据集

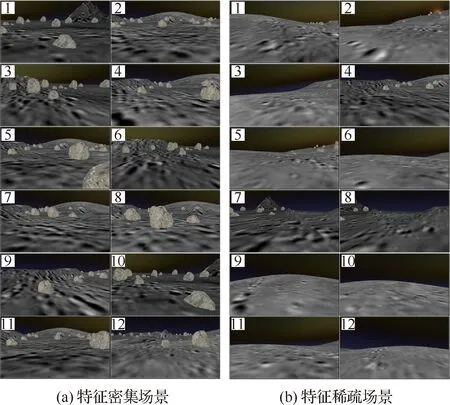
利用Gazebo仿真引擎，在WIP Moon Habitat开源模型库的基础上[21]，实现了一套模拟月面环境的计算机仿真系统。为了模拟多种不同场景的月面环境，在仿真模型库[18]的基础上进行改进，将原本固定的单一月面场景改进成可调节的多种月面场景。在搭建的月面环境仿真系统中，可以调节多种典型的月面场景元素的状态，进而模拟多种不同的月面场景，例如可以调节月面场景中陨石块的形状、尺寸、数量与空间分布等情况。通过调节不同月面场景元素的状态，能够模拟不同特征稀疏程度的月面场景，用于验证本文提出的视觉惯性SLAM方法的性能。

在仿真系统中，模拟了不同程度的特征稀疏的典型月面场景，包括沙质土壤、陨石坑、陨石块、环形山和起伏不平的山丘地形等典型月面场景元素，实现了一套较高仿真度的月面场景。其中，整个月面仿真场景的俯视图近似为正方形区域，月面场景规模大小约为：100 m×100 m，总面积约为1.0×104m2。

为了量化评估本文方法的定位性能，采用国际通用的视觉惯性里程计Benchmark EuRoC数据集的格式[22]，依据不同的最大移动速度、角速度和场景特征的稀疏程度，构建了3种不同难度的视觉惯性数据集，参数设置如表2所示。

构建的月面环境仿真数据集包括特征密集和特征稀疏等2种典型的环境。依据如表2中所示的数据集参数设置，构建了6组用于定位性能测试的数据集，图像总数约为1.8万张。其中，不同场景数据集的部分图像样本，如图5所示。

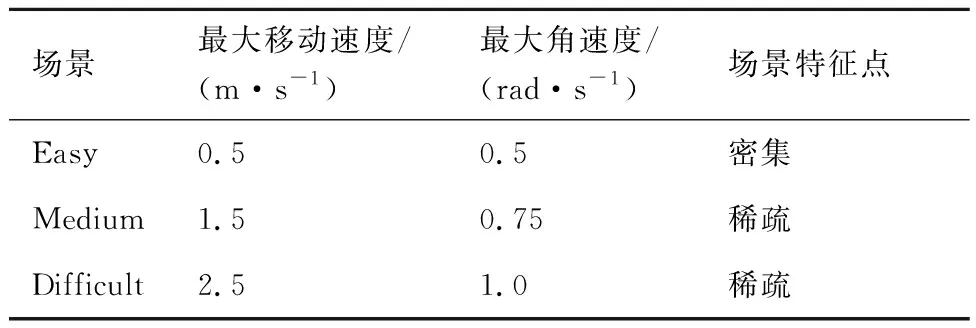
表2 数据集参数设置Table 2 Setting of dataset parameters

5.3 定位结果与分析

为了验证本文方法的定位性能，在多个不同的月面场景数据集下进行了仿真测试。通过仿真测试，验证了本文方法的有效性，并且量化分析了位移定位误差和姿态角估计误差。

5.3.1 位移定位误差

依据国际上通用的SLAM系统定位准确度评估方法[23-25]，采用绝对轨迹误差(Absolute Trajectory Error，ATE)的均方根误差(Root Mean Square Error，RMSE)作为定位准确度的定量评估指标[26-28]。在3种不同难度的场景下，利用一共6组数据集进行了定位性能的对比测试，位移定位准确度的仿真测试结果，如表3所示。

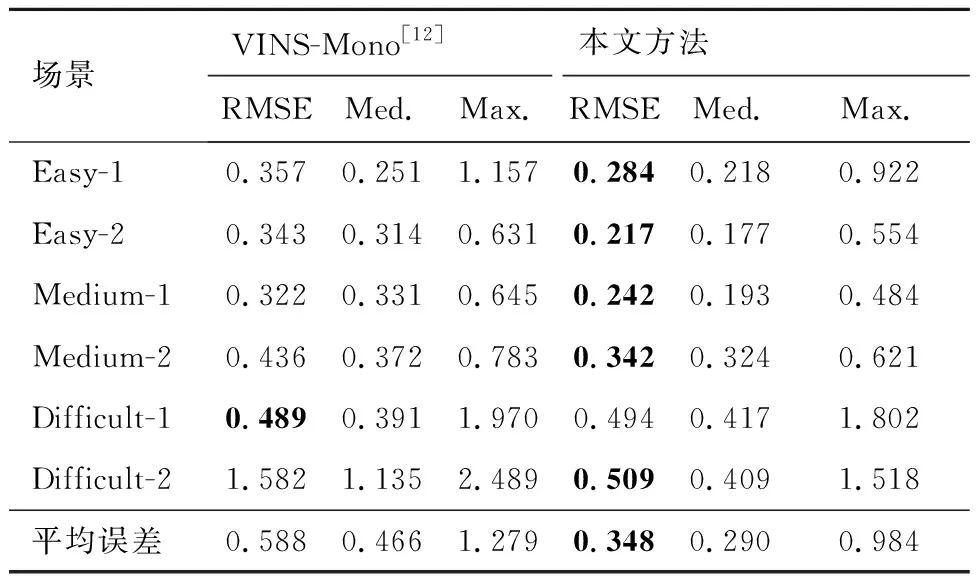
表3 位移定位误差比较Table 3 Comparison of localization errors m

本文方法在大部分数据集上的定位准确率均高于VINS-Mono[12]方法。其中，本文方法的平均定位均方根误差(RMSE)、平均误差的中值(Med.)和最大值(Max.)分别为0.348、0.290、0.984 m，平均定位误差均低于VINS-Mono[12]，本文方法实现了高精度的定位。

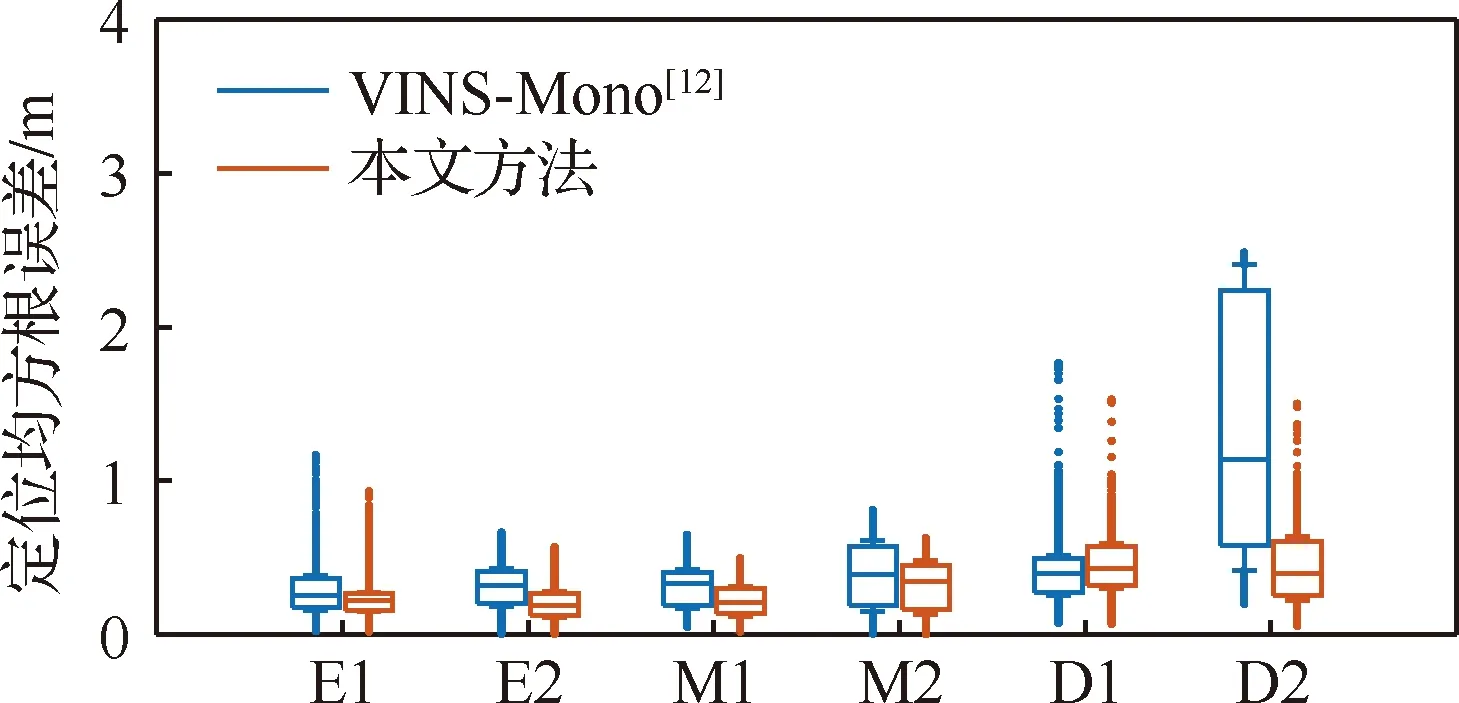
其中，用于定位仿真测试的6组月面数据集的移动轨迹总长度约为733.08 m。通过不同算法估计的轨迹和真实轨迹的均方根误差来比较算法的定位性能，绘制均方根误差的箱型图，如图6所示，横坐标分别为数据集序号的简写，例如E1为Easy-1数据集，依此类推。依据箱型图的均值可以发现，本文方法的均方根误差比VINS-Mono[12]方法更小，且定位误差有界，由于在D1数据集中，场景存在大量的纹理重复的区域，所以本文方法定位性能略低于VINS-Mono[12]。但是本文方法具有更好的鲁棒性，本文方法在快速运动、特征稀疏的D2数据集仍能够保持0.5 m左右的高精度定位，高于VINS-Mono[12]方法，且根据误差箱型图的分布可知，本文系统的定位误差的波动更小，定位估计具有更好的一致性，实现了误差有界的月面环境下准确、鲁棒的定位。

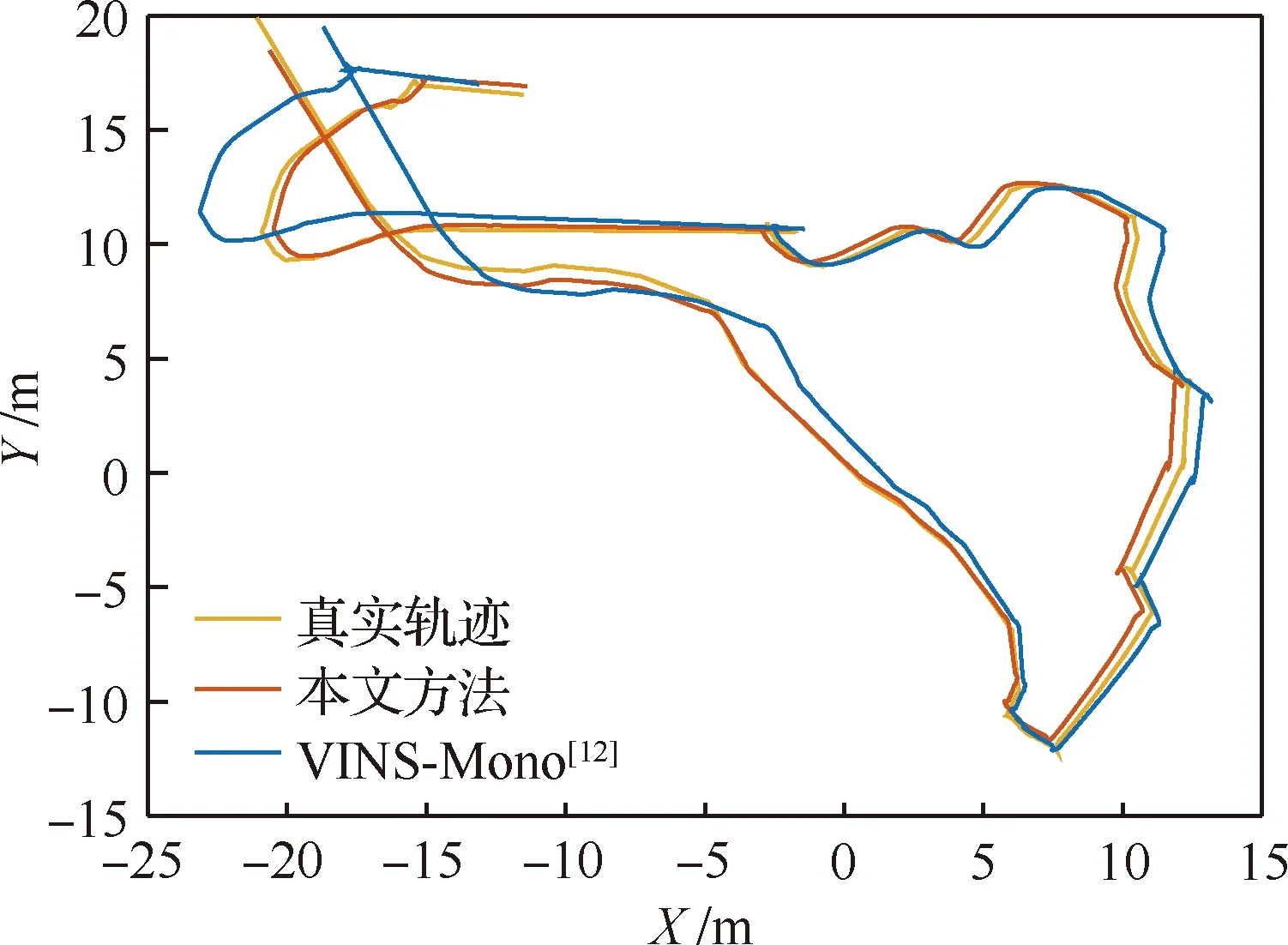
本文方法的定位轨迹能够更准确地接近真实轨迹，其中，在Difficult-2数据集的测试结果，如图7所示，本文方法的定位误差小于VINS-Mono，仿真测试结果表明本文方法的定位更准确。

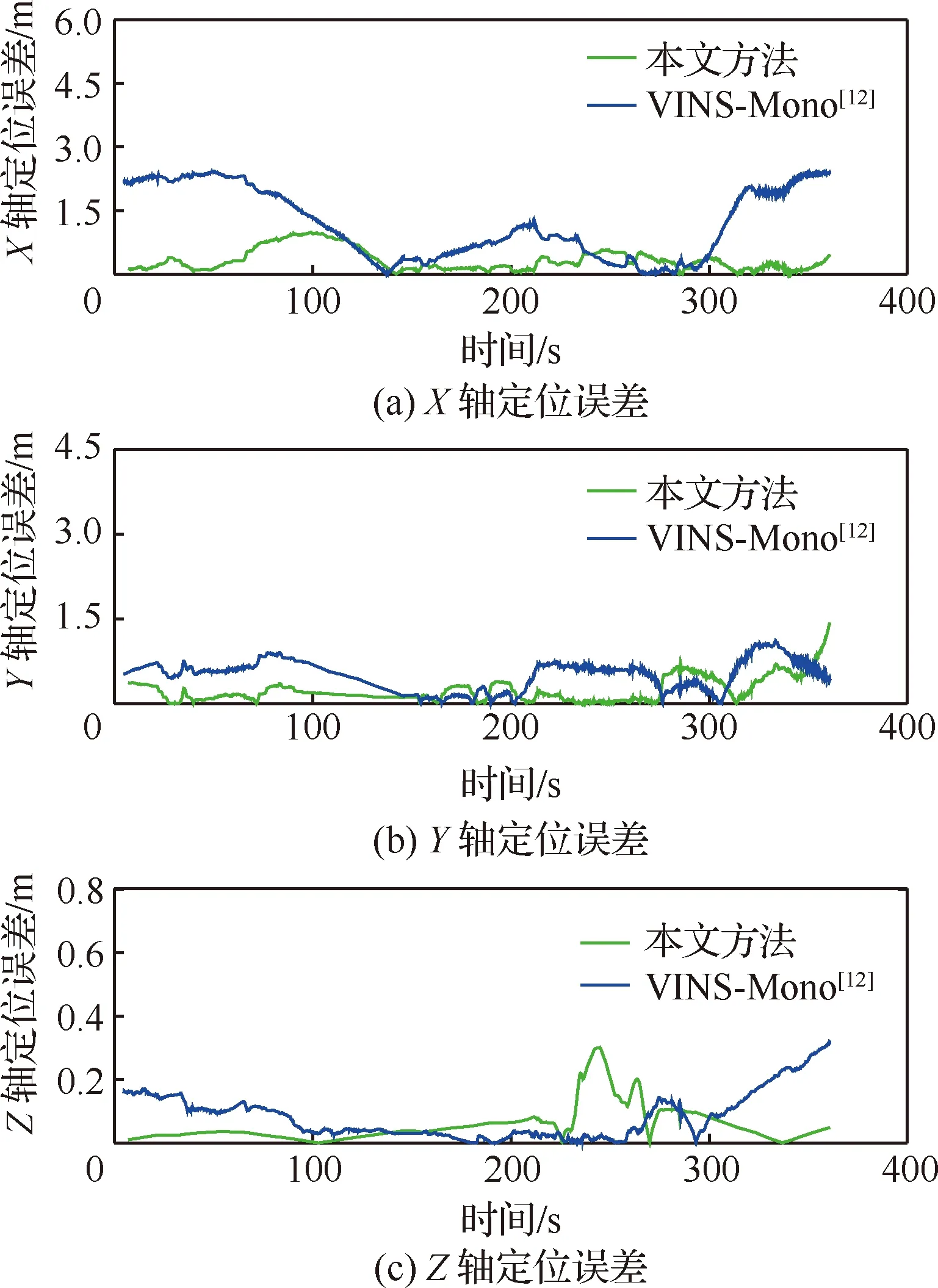
为进一步量化分析绝对位移的定位误差，选择Difficult-2场景数据集进行定位误差的量化分析，其中X、Y和Z轴的位移定位误差曲线，如图8所示，仿真测试结果表明，本文方法的平均定位误差的均方根误差约为0.509 m，在3个坐标轴方向的平均定位误差均小于VINS-Mono[12]方法。

5.3.2 姿态定位误差

针对姿态角估计情况，在上述6组不同的月面场景数据集下面进行了仿真测试，偏航角(Yaw)、俯仰角(Pitch)和滚转角(Roll)等姿态角度的估计误差如表4所示。本文方法在偏航角和滚转角的平均定位精度均高于VINS-Mono[12]，其中，只有俯仰角的平均误差略低于VINS-Mono[12]，并且整体姿态角估计的准确度均有一定程度的提升。

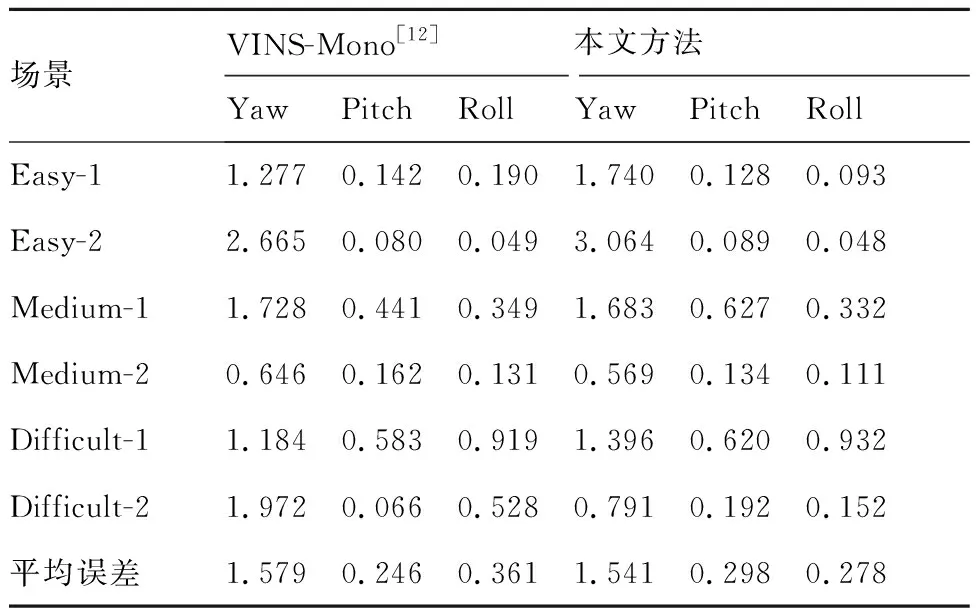
表4 姿态角估计误差比较Table 4 Comparison of attitude angle estimation errors (°)

其中，在Difficult-2场景数据集进一步地分析姿态角度估计误差，如图9所示，本文方法在偏航角和滚转角的角度的估计误差分别为0.791°和0.152°，均小于VINS-Mono[12]的1.972°和0.528°，且俯仰角误差仅为0.192°，本文方法实现了更加准确的姿态角估计，并且能够适应于不同的月面场景，具有更高的鲁棒性和准确性。