基于动力学RRT*的自由漂浮空间机器人轨迹规划

2021-03-27葛佳昊刘莉董欣心田维勇陆天和

航空学报 2021年1期

葛佳昊，刘莉，董欣心，田维勇，陆天和

北京理工大学宇航学院，北京 100081

随着人类对宇宙空间探索的不断深入，高效的后勤保障成为空间在轨服务的热点方向之一[1]，空间机器人成为低成本在轨运行的关键[2]。根据机器人基座的控制策略不同，可将空间机器人分为基座位姿固定、基座位姿机动、基座姿态受控和自由漂浮等模式[3]。自由漂浮空间机器人因节省燃料、姿态调整灵活等优点，有更高的实际应用价值，其轨迹规划问题是关键技术之一。

自由漂浮空间机器人(Free Floating Space Robot，FFSR)轨迹规划即对机械臂末端机械手的运动轨迹规划，需要在满足多体动力学系统动力学特性和非完整约束条件的同时避开障碍并到达目标位置，FFSR工作环境比地面机器人更为恶劣，轨迹规划更为复杂。关于FFSR模型，Vafa和Dubowsky[4]提出了基于虚拟机械臂(Virtual Manipulator，VM)的分析建模方法，实现了对FFSR运动/动力学方程的更简易描述。Dubowsky和Papadopoulos[5]建立了完整的自由飞行和自由漂浮机器人运动/动力学和控制模型。梁斌等[6]提出动态等效机械手(Dynamically Equivalent Manipulator，DEM)的概念，将FFSR转化为基座铰接的机械臂，以克服VM不能直观模拟空间机械臂的缺点。

根据规划模型的不同，FFSR的轨迹规划可大致分为基于运动/动力学模型规划和基于几何模型规划两类。

基于运动学模型的规划通常借助智能算法对FFSR轨迹规划进行求解，如粒子群优化算法[7-9]、遗传算法[10-11]和差分进化算法[12]等智能算法被用来规划得到单臂和双臂机器人运动轨迹；黄兴宏等[13]将非完整约束轨迹规划问题转化为最优控制问题，并采用牛顿迭代法得到全程恒定基座姿态零扰动的空间机械臂轨迹。基于运动学和动力学模型，FFSR轨迹规划问题通常转化为最优控制问题，戈新生和陈凯捷[14]采用Legendre伪谱法实现机器人轨迹规划；曾祥鑫[15]通过高斯伪谱法得到机器人移动轨迹，并以此为输入实现考虑机械臂挠性的FFSR姿态控制。基于DEM模型，Benevides和Grassi[16]引入双向策略的快速扩展随机树(Rapidly-exploring Random Tree, RRT)算法得到等效机械手的无碰撞轨迹，但是难以还原成FFSR的关节运动情况。Xu等[17]针对旋转目标的抓取问题，提出面向区域捕获的双臂空间机器人协调路径规划方法。至此，考虑高维非完整约束的FFSR轨迹规划问题已得到基本解决，但现有方法还存在着规划效率较低的问题。

另一类为仅考虑机器人几何模型的快速路径规划。贾庆轩等[18]采用A*算法实现了对机械臂轨迹的毫秒级避障规划，满足控制周期的实时性要求。阳涵疆[19]和邹宇星[20]等基于机械臂关节构形空间，分别采用RRT和改进的概率路线图法实现了对六自由度机械臂的无碰路径规划。谢碧云等[21]改进了双树随机树搜索算法的目标点树根生成机制，在不考虑机械臂末端姿态的情况下，实现了对典型空间冗余机器人的路径规划。仅考虑几何模型可以较快得到可行路径，但规划结果不满足系统动力学特性。

为提高考虑运动/动力学模型的FFSR轨迹规划效率，提出一种基于动力学RRT*算法的FFSR轨迹规划方法。首先，将FFSR的运动/动力学方程伪线性化为机械手状态方程，并设计同时考虑关节能量消耗和轨迹完成时间的代价函数。其次，为提高碰撞检测效率，针对机械手初末位置间障碍，提出机械臂避障和机械手避障的两层次避障策略，并设计FFSR动力学RRT*轨迹规划器。最后，以2自由度(Degree of Freedom，DoF)自由漂浮空间机器人的轨迹规划为例进行数值仿真。结果表明，采用动力学RRT*方法可在较少的迭代步数内得到可行解，随迭代步数增加，可获得渐进最优轨迹，具有较高的求解效率。

1 FFSR轨迹规划问题假设及模型

选用单臂自由漂浮机器人通用模型，如图1所示。图中：CM为机器人的质心位置，并将其选为惯性系坐标原点；CMi为FFSR各部件的质心位置；Pi为第i个机械臂关节；ρi为各部件质心在惯性系的位矢；qi为各部件的相对转角，正方向规定如图1所示；ri为第i个部件质心到下一个关节的位矢；li为第i个部件质心到前一个关节的位矢。

图1 单臂FFSR通用模型Fig.1 General model of single arm FFSR

1.1 FFSR模型

自由漂浮模式下，系统线动量、角动量守恒：

(1)

(2)

由式(1)和式(2)可得

(3)

末端机械手的坐标可表示为

ρE=ρn+rn

(4)

对式(4)求导可得系统运动学方程为

(5)

式中：J(q)为FFSR的广义Jacobian矩阵。

忽略重力，考虑系统拉格朗日方程和总动能：

(6)

可得系统动力学方程：

(7)

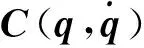
1) 忽略重力，忽略太阳风等阻力，FFSR始终动量守恒且初始动量为0。

2) 忽略FFSR部件挠度，各部件间由一个单自由度关节连接，每个关节仅受一台电机控制。

3) 系统质量参数已知，运动状态可观测。

4) 基座质量远大于机械臂杆质量，且FFSR运动缓慢，故当前节点的机器人位姿可作为到下一个节点间状态的估计值。

1.2 系统线性化

由式(5)和式(7)可得

(8)

式中：H(q)为对称正定矩阵，其逆矩阵必存在。

本研究结果也显示，观察组患者Baumann角、临床效果、手术时间等均优于对照组，差异有统计学意义（P＜0.05），这是因为小切口辅助复位经皮克氏针固定治疗中，切口能够有效避免太靠上，减少对桡神经的损伤，同时术中能够有效保护干骺端骨膜，从肱骨小头进针会事先扪清确定尺神经沟，进而避免了因手术操作对尺神经的损伤，术后会依据情况予以患者抗生素或者引流。

(9)

假设4)保证每个节点之间都可近似为线性系统。

1.3 代价函数

选取以权系数μ∈[0，1]加权的Bolza形式性能指标作为代价函数，在应用过程中，可通过调整权系数使FFSR具有更大工作灵活性。代价函数为

minJ=μJ1+(1-μ)J2

(10)

式中：J为总代价函数；J1和J2分别为使位姿调整过程中能量消耗最小的Lagrange型性能指标和增强位姿调整的时效性的Mayer型性能指标：

(11)

(12)

式中：tf为机器人位姿调整最终时间；R为指定的正定常数矩阵，代表控制输入成本的权衡；t0为系统初始时刻。

2 FFSR系统的避障轨迹规划

FFSR是典型的非完整多体动力学系统，系统表现出的高维度和非完整特性增加了路径规划的难度与控制的复杂性。规划时不应只考虑几何避障，也应考虑系统动力学特性。

对于实际应用，强调轨迹规划的效率和轨迹的可行性而非最优性。相比于图搜索方法(如A*和D*等)、局部规划算法(如人工势场法等)和求解最优控制问题的伪谱法等，RRT*算法作为一种基于采样的规划方法，可通过重选父节点和重布线等操作降低路径代价，有效提高算法效率，在考虑对象非完整约束限制的条件下，快速搜索解空间并得到可行轨迹，对FFSR轨迹规划具有较高的适应性。因此，加入机器人动态约束的RRT*算法在收敛的时效性和高维问题求解的适应性方面独具优势。

2.1 最优轨迹的计算

对于能控线性质点系统，动力学RRT*算法[23]通过求得最短抵达时间的闭式解，构造末状态固定、抵达时间自由的轨迹规划问题，自由给定抵达时间以降低代价函数值。对于非线性系统，每次迭代时围绕假定平衡点一阶泰勒展开为能控线性系统。作为运动非线性强的多体动力学系统，采用上述方法不能准确描述FFSR运动状态。

针对此问题，采用伪线性化方法得到解析的FFSR状态空间模型，相比于文献[23]，模型描述更精确，适用范围更广，迭代时只需代入新广义关节角值即可更新模型，提升运算速度，使规划过程更简洁快速，规划结果更加符合实际。

对于能控的离散动力学系统：

(13)

式中：u(t)为系统输入；x0为系统初始状态。

2.1.1 最优抵达时间求解[23]

对于末状态x(tf)=x1固定、机器人位姿调整最终时间tf固定的最优控制问题，构造Lyapunov函数：

(14)

其闭式解为加权能控的Gramian矩阵：

exp(AT(t-t′))dt′

(15)

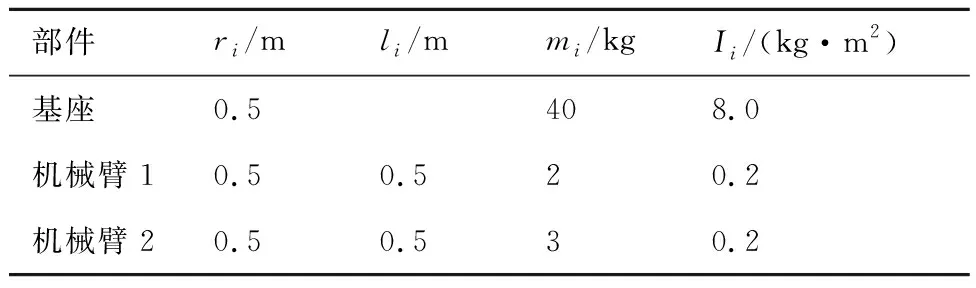
式中：t′为时间变量t之前的某时刻(t′

那么，最优控制输入为

u(t)=R-1BTexp(AT(tf-t))d(tf)

(16)

将式(16)代入式(13)，得到代价函数的闭式解：

(17)

(18)

经式(18)计算得到最优的抵达时间，那么，原问题扩展为了末状态固定且抵达时间自由的轨迹规划问题。

2.1.2 最优轨迹的计算[23]

令y(t)=exp(AT(tf-t))d(tf)，则有：

u(t)=R-1BTy(t)

(19)

将式(19)代入式(13)，得到复合微分方程：

(20)

从而得到最优轨迹的状态量与控制输入为

(21)

(22)

至此，得到的状态量和输入量实现了对最优轨迹的唯一确定。

2.2 FFSR避障策略

仅考虑机械手初末位置间存在障碍的情况。Rybus[24]总结了空间机器人避障的发展现状，为进一步简化计算，将障碍物抽象成长方体(在2维空间内为矩形)；为保证运动安全性，对障碍物进行膨化作为真实障碍。

提出FFSR机械臂避障与机械手避障两层次避障策略。若机械臂与障碍物干涉或机械手位于障碍物内部，则认为机器人与障碍碰撞。

2.2.1 机械臂避障策略

若每次通过求解机械臂几何位置判断是否与障碍干涉，会大大增加计算量，降低算法效率。因此，对于单臂自由漂浮机器人通用模型，结合工程应用实际，采用障碍几何延拓的策略避免机械臂碰撞。

如图2所示，对原障碍进行膨化，面a为膨化后障碍距离机器人最近的面，基于面a将障碍延拓至机械手可达最远端。那么，原可行的轨迹a、b中仅有轨迹a可行。

图2 机械臂的避障策略Fig.2 Obstacle avoidance strategy of robotic arms

2.2.2 机械手避障策略

如图3所示，对原障碍进行膨化。机械手当前的位置为点1，E为点1与障碍四角连线的包络区域，其他点为机械手下一状态点xnew。点2位于E外，点3位于E内点1与障碍之间，点4位于障碍内，点5位于E内障碍后方。易得，位于点4、5时轨迹不成立。

图3 机械手的避障策略Fig.3 Obstacle avoidance strategy of manipulator

2.3 动力学RRT*规划器

将FFSR伪线性模型与两层次避障策略融入动力学RRT*算法，使其具备对多体系统的规划能力。设计基于FFSR多体运动学与动力学的RRT*算法求解器，以找到式(21)和式(22)定义的最优轨迹。通过较少的迭代次数获得轨迹的可行解，随着迭代次数增加，轨迹逐步趋向最优。

图4为求解器节点生成及随机树更新示意图图中r为搜索子节点时设置的邻域半径。结合图4，给出算法步骤流程如下。

步骤1设迭代次数k=1，xstart和xgoal分别作为轨迹的初末状态点。

步骤2在第k次迭代时，在随机树上各状态节点x处更新FFSR系统伪线性模型并获得对应的代价函数值cost[x]，以x为父节点生成新的随机状态点xrand。

步骤3碰撞检测。若发生碰撞，则重新生成随机状态点并进行步骤3；反之，设xrand为合法随机状态点xnew。

步骤5随机树重新布线。对已有状态点及xgoal，在满足避碰条件下，若cost[xnew,xnear]

步骤6判断随机树是否已延伸至xgoal，若是，则可行轨迹生成，算法可停止；若否，则转至步骤7。若希望完成全部迭代次数，则忽略步骤6，转至步骤7。

步骤7根据节点间父子关系求解轨迹，更新随机树；k+1→k，转至步骤2，如图4(c)所示。

考虑到FFSR状态方程的系统矩阵A为幂零矩阵，exp(At)可表达为一个n-1自由度的矩阵多项式；因此，由式(15)、式(17)、式(21)和式(22)可得到确定的闭式多项式解，最优轨迹可解析表达。那么，规划得到的轨迹也可用多项式平滑连接。与经典RRT*算法不同的是，规划过程中轨迹直接延伸至新的可用随机点，而不是向新的可用随机点前进固定距离，这样可以快速连接初末位姿，得到可行轨迹，进而根据代价函数值更新或更新随机树以获得更优轨迹。

图4 节点生成及随机树更新示意图Fig.4 Schematic diagram of node generation and random tree updating

迭代期间通过式(3)和式(23)求解机器人状态信息：

(23)

为提高运算速度，算法采用Doolittle分解法对式(9)的H-1(q)进行求解。

3 仿真验证与结果分析

为在验证所提方法有效性的同时不失一般性，选取简化的平面2连杆自由漂浮机器人作为研究对象，此模型能够充分证明设计理论的概念和性能，已广泛应用于空间机器人理论验证[15]。

3.1 仿真参数和结果

系统的模型参数如表1所示。

表1 2连杆FFSR模型参数Table 1 Parameters of 2DoF FFSR model

仿真是基于PC机(3.41 GHz/Core8)上的MATLAB R2019b进行。仿真迭代次数选取1 000次。对μ=0, 0.5, 1.0这3种目标情况进行数值仿真。仿真结果如表2和图5所示。

表2 迭代1 000次的规划结果Table 2 Planning results of 1 000 iterations

结合表2，从系统沿轨迹规划结果运动过程图(图5(a)～图5(c)，采用FFSR部件颜色的由浅至深表明系统从起点运动到目标点的时序变化)上看，生成的轨迹光滑且满足约束条件，能有效避开障碍，并以预设的状态到达目标点。观察可发现，能量消耗最低的轨迹最贴近障碍物，过程调整幅度最小；调整时间最短的轨迹偏离障碍物的距离最远，过程调整幅度最大。其原因在于:为了使能量消耗最低，电机扭矩的数值和变化幅度小(图5(g))，姿态变化幅度小，使得轨迹完成的时间长，轨迹贴近障碍；调整时间最短的轨迹则相反，电机的扭矩输出和变化幅度较大，甚至到达扭矩的约束边界(图5(h))，FFSR姿态调整速度快，姿态调整幅度大(图5(e))，使得轨迹完成的时间短，轨迹偏离障碍较远；能量消耗和调整时间折中的轨迹规划结果则在姿态调整幅度(图5(f))、所需时间和电机扭矩输出(图5(i))等方面指标居中，符合代价函数设置预期。此外，对于不同权系数，初末位置关节角角速度和加速度近似为0，规划结果符合工程应用需要。

图5 能量消耗最低、调整时间最短和两者折中时的轨迹、关节角和电机扭矩Fig.5 Path, joint angle, and motor torque with minimum energy consumption, minimum adjusting time, and tradeoff between energy consumption and adjusting time

3.2 仿真结果分析

3.2.1 渐进最优性

为了验证规划方法的渐进最优性，选取上述代价函数权系数μ=0.5的算例(迭代次数1 000 次)，最终代价函数值为2.901 6。代价函数值随迭代次数增加的变化情况如图6所示。结果表明，代价函数值随迭代次数的增加逐步降低，可得到从初始位姿到期望位姿的渐进最优调整轨迹。

图6 代价函数值与迭代次数的关系Fig.6 Cost function value versus number of iterations

3.2.2 算法有效性

在实际应用时，通常不需要最优轨迹而是快速得到可行轨迹。如图6所示，在第13次迭代时，生成了有效的代价函数值，即此时生成了可行的轨迹。根据式(23)，最初得到的轨迹误差较大，随着迭代次数的增多，路径上随机点数增多，误差逐步降低。值得注意的是，快速随机扩展类方法的随机性影响了生成可行轨迹的迭代次数，但是经多次计算，在此场景下，算法迭代35次以内可得到可行轨迹，且单次迭代时长约0.61 s。

3.3 算法对比

选取经典RRT*算法、高斯伪谱法与本文算法对比。本文算法与高斯伪谱法均包含系统动力学模型，代价函数选为姿态调整时间最短；而经典RRT*算法仅能考虑FFSR的关节几何约束，不包含动力学信息，难以获取姿态调整时间及能量消耗，代价函数为路径最短。将三者结果进行对比，自由漂浮机器人的初末位姿与障碍物特征相同。其中，经典RRT*算法节点数为分别为3 500与5 000，步进长度为0.005 m；高斯伪谱法的配点数分别为20与30。

图7为各方法规划得到的末端机械手路径对比，由对比可得，高斯伪谱法可得到规划的最优解；经典RRT*规划得到的路径更短，但是由于无法考虑系统动力学特性，因而规划得到的路径不平滑，难以满足系统动力学约束，不能保证运动的连续性。